Pytorch ---- 反向传播 学习笔记~~~~~

前两天学习了线性模型，穷举权重和使用梯度下降法求权重。
今天学反向传播。

反向传播损失公式：

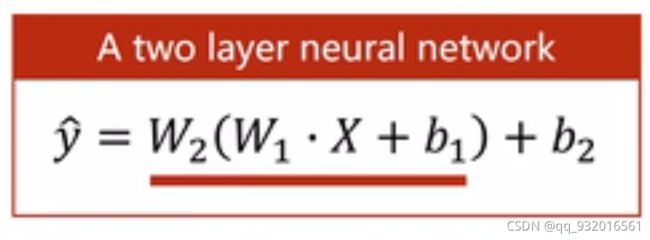
W1为权重矩阵。
b1（bias）为偏置向量。

解释一下为什么这里的W不再是前面学过的单一的权重值而是变成了矩阵。

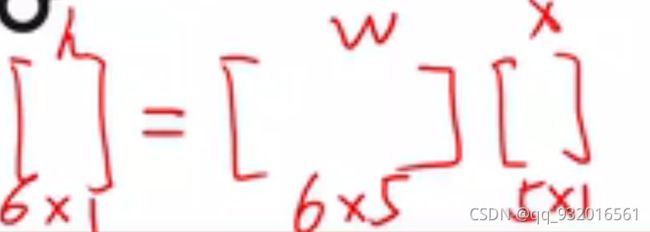
从下图中可以看到，当神经网络有很多层的时候，输入值X也有很多。其中每一个X都对应着后面的一个Y。

看下面这张图，显然在第一层，权重W为6*5的矩阵，共30个值。

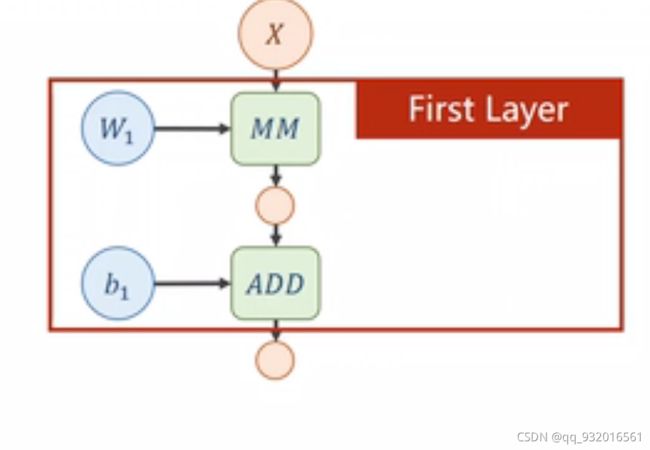
下图为全连接神经网络中的一个层。
MM为矩阵乘法。
ADD为向量加法。

这时候再回头看一下公式:

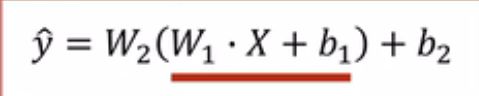
使用第一层的权重W1乘以输入值X加上偏移量b1，得到输出。

第一层的输出作为第二层的输入，做同样的运算，第二层的权重W2乘以输入值X加上偏移量b2。得到的输出给第三层，作为第三层的输入，，，以此类推。。。。。。。。

对上面式子进行化简可以发现，W2和W1最后都会化简掉。

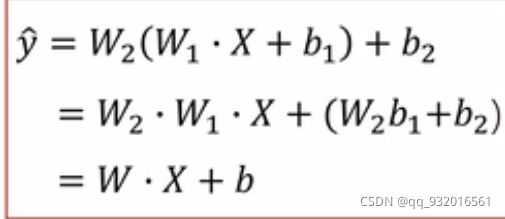
所以这些这么多的隐层是没有什么意义的。
所以在每一次变换中加入非线性变换，让上面的式子无法化简。

下图为正向传播:
绿色方块中为函数算法，这里假设为 X * W

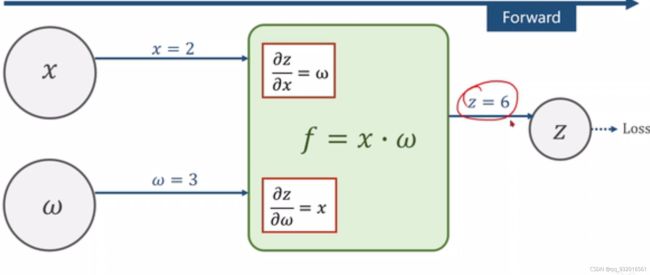
正向传播后得到了Z，也就是绿色方块中算出来的函数f的值。
然后我们算出来损失值。

假设从后面传到本层的损失值对Z求偏导得到的数为5.。
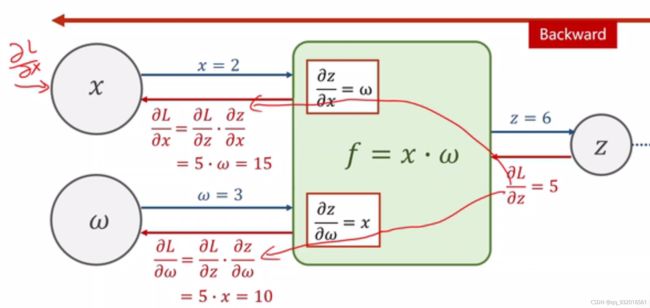
那么按照绿色方块中了两个算法路径传回去。

可以由链式求导法则得到相应的L对X求偏导和L对W求偏导的值。求出输入量X和W的梯度。然后更新对应权重。这两个值又可以传到再前面一个层去。

注意:这里是整个神经网络中的一个层。他有上一层，也有下一层。
在Pytorch中 将梯度存在变量中，有些算法将梯度存在绿色的模块中。

来看一个实例：
使用线性模型 y = x * w
要训练权重w的值。

第一步:
表示 w * x 得到 y(预测值)。
绿色方块中为乘法操作。

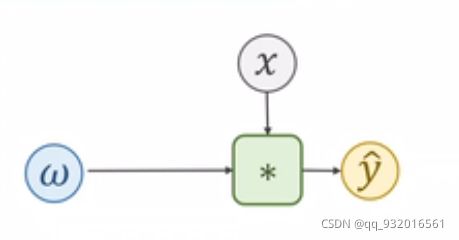
设 w = x = 1 则 y(预) = 1
第二步:
根据损失函数 (x * w - y ) ^ 2 算出损失值loss。
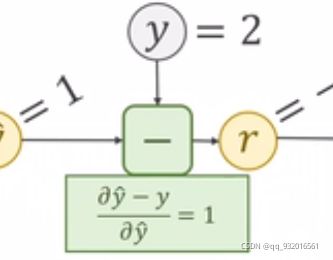
设真实值y(真) = 2。

此时的r = x * w - y(真) = -1。
这里的r叫做残差(residnal)。

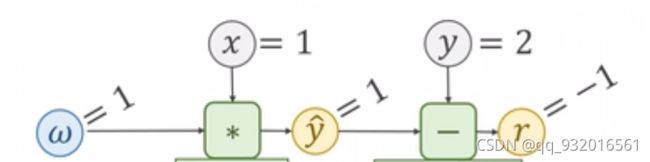
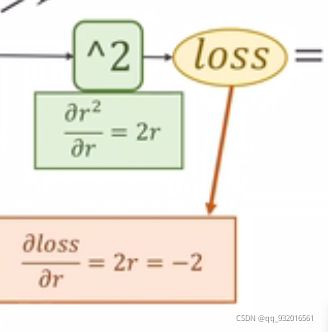
然后我们再进行平方操作 得到 loss = r ^ 2 = 1

此时正向传播完毕。
下面开始反向传播:
这时候要明白我们的目的是要训练W的值，即每次层要使用梯度更新权重的值，所以要求的损失函数对w的梯度(即导数)。
由链式求导法则进行展开,

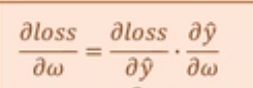
这个式子我们可以看出来，y(预)对w求导可以由上面正向传播 的第一步求得.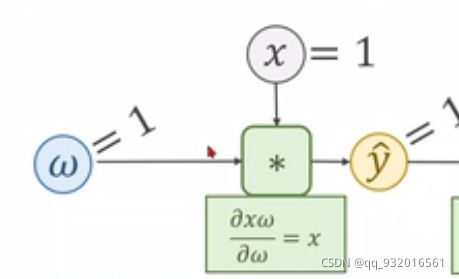
所以我们只需要求的损失loss对y(预)的导数。

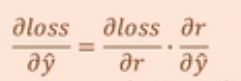
同样，在正向传播的第二步可以求出r对y(预)的导数，
此时只需要求出损失值loss对r的导数。

同样在正向传播的最后一部可以求出loss对r的导数。

这时候就可以求出来我们要的损失函数loss对权重值w的导数。
上面是理解的过程，在程序中直接就是正向(前馈)一趟，反向一趟即可求出结果。
在Pyrotch中，上面的所有数据都存在 Tensor里。

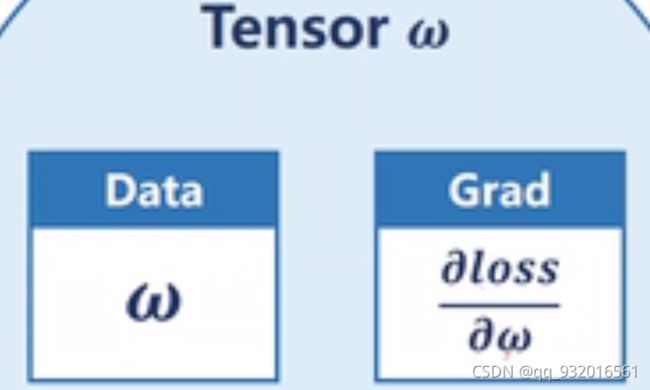
Tensor里的两个成员，一个是权重值W。另一个存损失对权重的导数，即梯度。其中Grad也是一个Tensor里面也有data。

先贴代码 后面解释:

import torch
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
a = 0.01  # 学习率
# 反向传播
w = torch.Tensor([1.0])  # 设置初始权重值
w.requires_grad = True  # 确定计算梯度


# 计算单个数据的损失值
def loss(x_val , w,y_val):
    return (x_val * w - y_val) ** 2
ll_w = []
ll_loss = []
if __name__ == '__main__':
    for i in range(100):
        for x_val,y_val in zip(x_data,y_data):
            l = loss(x_val,w,y_val) # 计算损失值
            ll_w.append(w.item())
            ll_loss.append(l.item())
            l.backward()    # 反向传播
            w.data = w.data - a * w.grad.data # 更新权重
            w.grad.data.zero_() # 清除梯度数据

print(ll_w)
print(ll_loss)
plt.rcParams['font.sans-serif'] = ['KaiTi'] # 解决结果中字体显示不完全的问题
plt.plot(ll_w,ll_loss)
plt.xlabel("损失loss")
plt.ylabel("权重")
plt.show()

这里的W已经不是前面的一个数了。而是一个张量，原因前面已经说过了，所以使用torch.Tensor定义 并给定初值为1.0 w = torch.Tensor([1.0])

这里所有张量的使用都是在torch里构造前面说过的计算流程图。如果想使用某些数据，要用item()或者data这样。

比如本程序中每次计算了单个样本的损失值。如果我们想像前面一样计算MSE总体的损失值，使用了sum记录总体，然后用sum +=l 这种写法会直接崩。
因为l接收的是loss损失值。在前面做 x * w的时候(标量 * 张量)得到的是一个张量。所以在后面调用loss的时候 返回给l的也是一个张量。如果使用sum +=l 则程序会一直构造计算流程图在电脑内存中，直到吃光内存，。。。
所以如果有这样的需求。可以这样写sum+= l.item()。

得到结果：