Pytorch框架学习个人笔记4---反向传播

提示：本博客是依托B站【刘二大人】的讲解视频并结合个人实践学习总结而成，仅用作记录本人学习巩固，请勿做商用。

---

前言

这一讲主要介绍的是反向传播算法。反向传播的概念我们在第一讲简单的提到过【传送门】

---

一、原理回顾

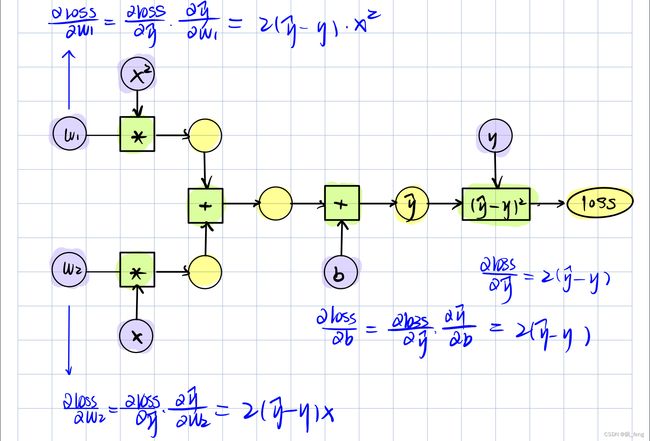
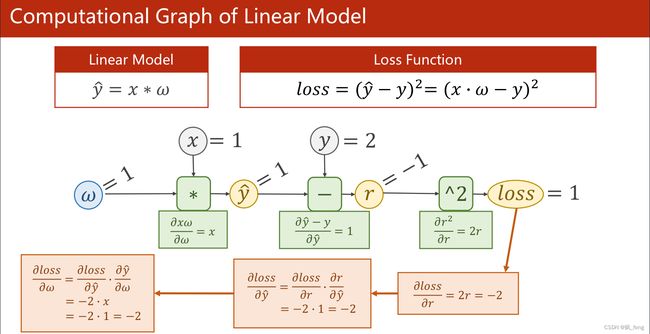
以学习过的线性系统为例，先按照计算图进行前馈过程的运算（包括data和grad）然后根据求导的链式法则计算出loss( )的导数。

二、激活函数

在多层神经网络中，上层节点的输出和下一层节点的输入之间具有一个函数有关系，这个函数被称为激活函数。
在没有引入激活函数之前，输入和输出都是线性组合，跟没有隐藏层的效果是一样的，网络不易收敛的，学习能力有限，就比如原始的感知机一样。激励函数的作用相当于引入了非线性函数，使模型更易于收敛，神经网络的逼近能力就更加强大。
对于不同类型激活函数的特点与区别，将在以后的博客中详述。

三、张量

张量（tensor）是多维数组，目的是把向量、矩阵推向更高的维度。
在pytorch11.0中，Tensor和tensor都用于生成新的张量，但二者在原理上是有区别的。

1. torch.Tensor()是Python类

import torch
a=torch.Tensor([1,2])
print(a.type())

#结果
torch.FloatTensor

2. torch.tensor()仅仅是子函数：

torch.tensor(data, dtype=None, device=None, requires_grad=False)

其中data可以是list, tuple, NumPy ndarray, scalar和其他类型，比如：

import torch
b=torch.tensor([1,2])
print(b.type())
c=torch.tensor([1.,2.])
print(c.type())

#结果
torch.LongTensor
torch.FloatTensor

这两种表示，我更倾向于后者。

四、代码实现

import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
 
w = torch.tensor([1.0]) # w的初值为1.0,其中data是tensor,初始grad为None
w.requires_grad = True # 需要梯度值
 
def forward(x):
    return x*w  # 权重是一个tensor
 
 
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y)**2
 
print("predict (before training)", 4, forward(4).item())
 
for epoch in range(100):
    for x, y in zip(x_data, y_data):
        l =loss(x,y) #调用loss(),计算前馈建立计算图，l是一个tensor
        l.backward() #内置函数，计算图被释放
        print('\tgrad:', x, y, w.grad.item()) #item取出的是标量，不建立计算图
        w.data = w.data - 0.01 * w.grad.data   # 权重更新时，注意grad也是一个tensor，取data不会建立计算图
 
        w.grad.data.zero_() #权重更新后为了避免累加，所以要置零
 
    print('progress:', epoch, l.item()) # 取出loss使用l.item，不要直接使用l（l是tensor会构建计算图）
 
print("predict (after training)", 4, forward(4).item())

运行结果：

predict (before training) 4 4.0
	grad: 1.0 2.0 -2.0
	grad: 2.0 4.0 -7.840000152587891
	grad: 3.0 6.0 -16.228801727294922
progress: 0 7.315943717956543
	grad: 1.0 2.0 -1.478623867034912
	grad: 2.0 4.0 -5.796205520629883
	grad: 3.0 6.0 -11.998146057128906
progress: 1 3.9987640380859375

...
...
...
    grad: 1.0 2.0 -7.152557373046875e-07
	grad: 2.0 4.0 -2.86102294921875e-06
	grad: 3.0 6.0 -5.7220458984375e-06
progress: 98 9.094947017729282e-13
	grad: 1.0 2.0 -7.152557373046875e-07
	grad: 2.0 4.0 -2.86102294921875e-06
	grad: 3.0 6.0 -5.7220458984375e-06
progress: 99 9.094947017729282e-13
predict (after training) 4 7.999998569488525

收敛效果好。

五、作业

计算图：

代码实现：

import torch

x_data = [1.0, 2.0, 3.0]
y_data = [4.0, 9.0, 16.0]

w1 = torch.Tensor([1.0])
w1.requires_grad = True#
w2 = torch.Tensor([1.0])
w2.requires_grad = True
b = torch.Tensor([1.0])
b.requires_grad = True

def forward():
    return w1 * x ** 2 + w2 * x + b

def forward(x):
    return w1 * x**2 + w2 * x + b

def loss(x,y):
    y_pred = forward(x)
    return (y_pred-y) **2

print('Predict (befortraining)',4,forward(4))

for epoch in range(1000):
    for x,y in zip(x_data,y_data):
        l = loss(x, y)
        l.backward()
        print('\tgrad:',x,y,w1.grad.item(),w2.grad.item(),b.grad.item())
        w1.data = w1.data - 0.01*w1.grad.data
        w2.data = w2.data - 0.01 * w2.grad.data
        b.data = b.data - 0.01 * b.grad.data
        w1.grad.data.zero_()
        w2.grad.data.zero_()
        b.grad.data.zero_()
    print('Epoch:',epoch,l.item())

print('Predict(after training)',4,forward(4).item())

结果：

...
...
    grad: 1.0 2.0 0.31661415100097656 0.31661415100097656 0.31661415100097656
	grad: 2.0 4.0 -1.7297439575195312 -0.8648719787597656 -0.4324359893798828
	grad: 3.0 6.0 1.4307546615600586 0.47691822052001953 0.15897274017333984
Epoch: 99 0.00631808303296566
Predict(after training) 4 8.544171333312988

可见收敛效果并不好，预测值与真实值相差甚远。
如果我们将训练轮数扩大至1000轮，结果：

...
...
grad: 1.0 2.0 0.19651126861572266 0.19651126861572266 0.19651126861572266
	grad: 2.0 4.0 -1.0207176208496094 -0.5103588104248047 -0.25517940521240234
	grad: 3.0 6.0 0.8323431015014648 0.2774477005004883 0.0924825668334961
Epoch: 999 0.0021382563281804323
Predict(after training) 4 8.325754165649414

有所改善但收敛效果也不好，原因是数据集为一次函数，噪声过大。
如果我们将数据集修改为：

x_data = [1.0, 2.0, 3.0]
y_data = [4.0, 9.0, 16.0]

结果：

    grad: 1.0 4.0 0.091766357421875 0.091766357421875 0.091766357421875
	grad: 2.0 9.0 -0.476654052734375 -0.2383270263671875 -0.11916351318359375
	grad: 3.0 16.0 0.3886756896972656 0.12955856323242188 0.043186187744140625
Epoch: 999 0.0004662616993300617
Predict(after training) 4 25.152122497558594

所得值与真实值相比差值为0.152122497558594，收敛效果有所改善，但还是有差距。

---

总结

但愿在后续的学习中能够习得效果更好的训练模型。