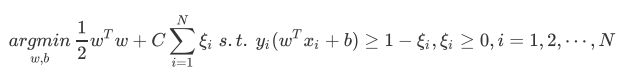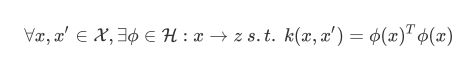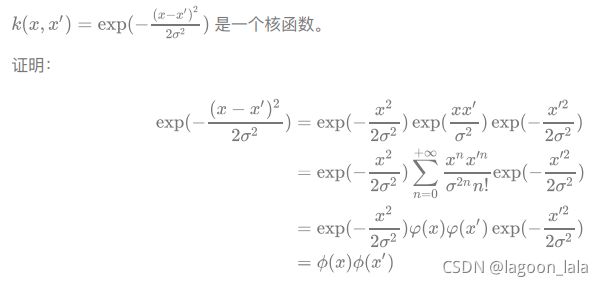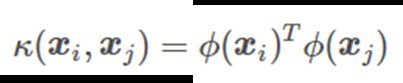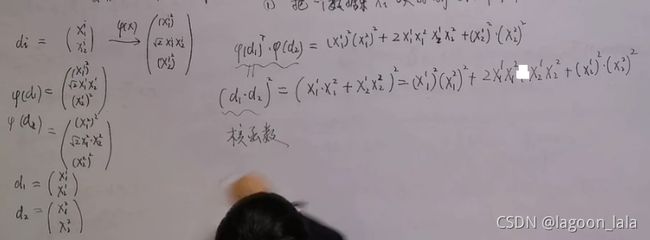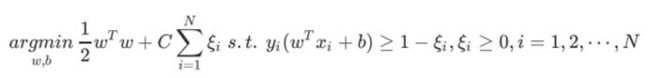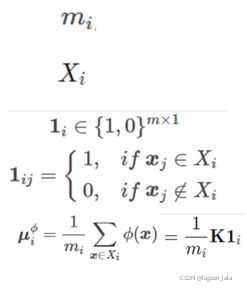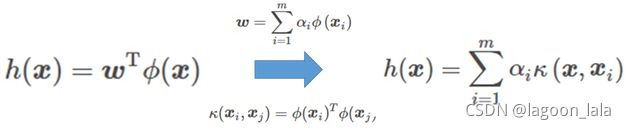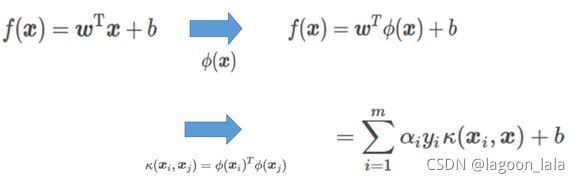核函数与核方法整理

一些之前提到过的知识, 对核函数相关进行详细梳理和串联.

根据胡老师建议的重点, 学习了一下:

核函数公式，作用，选择, 调参, 如何简化运算

目录

SVM回顾

严格线性可分问题

近似线性可分

核函数

什么是核函数

如何使用核函数

为什么要用核函数

核⽅法

常用符号

KLDA

SVM

KPCA

MMDE

---

SVM回顾

SVM能解决的三种分类问题:

严格线性可分

近似线性可分

严格非线性可分

严格线性可分问题

可以使用

感知机算法或硬间隔SVM

感知机算法

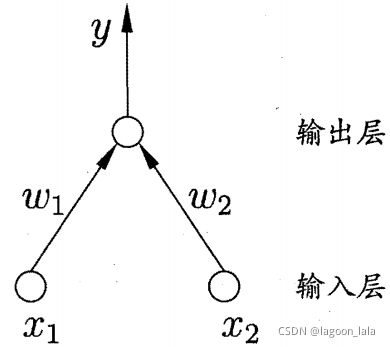
感知机 (Perceptron)由输入输出两层神经元组成, 

输入层接收外界输入信号后传递给输出层， 

输出层是 M-P 神经元，亦称"阈值逻辑单元" (threshold logic unit).

  

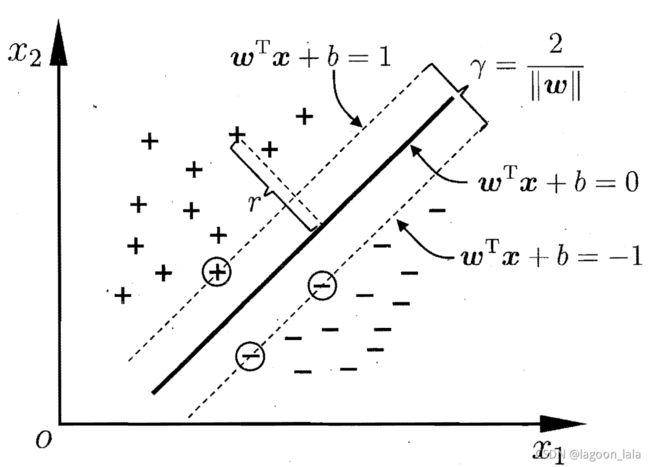
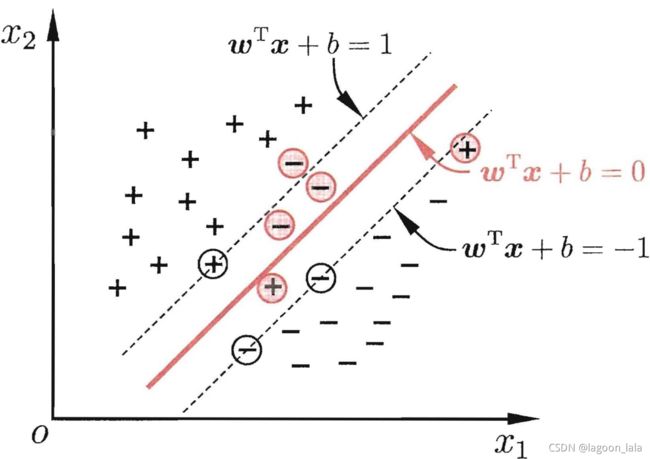
硬间隔SVM

支持向量: 距离超平面最近的几个训练样本对应特征向量

间隔(margin): ，两个异类支持向量到超平面的距离之和

近似线性可分

允许一点错误, 缓解非严格线性与过拟合问题

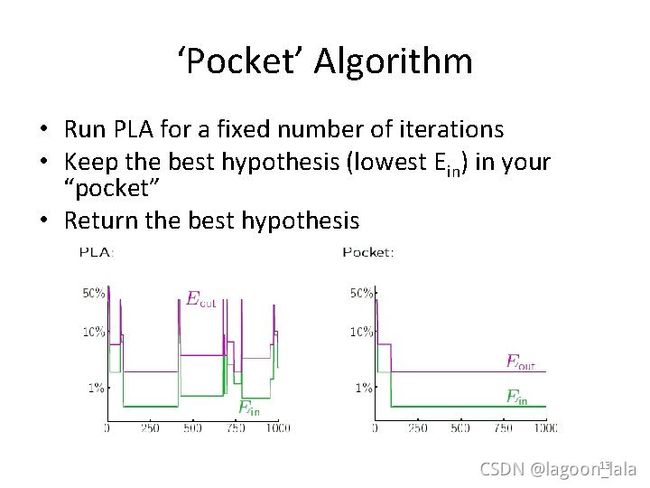
Pocket Algorithm

(对PLA改进)

如果我们无法保证样本是线性可分的，那么根据感知机算法执行的计算机程序可能会永远找不到合适的划分边界，陷入无限迭代之中。

口袋算法

预先规定迭代上限k

1、执行感知器算法，将假定的划分平面放入“口袋”存储起来。

2、对划分平面执行最优化算法( 例如，梯度下降 )，并得到新的划分平面与“口袋”里的划分平面进行比较。将划分效果比较好的划分平面放入“口袋”存储起来，取代原来存储在“口袋”中的划分平面。

软间隔

同时考虑

1. 最大化间隔(结构风险);
2. 最小化(软间隔支持向量)不满足约束的损失(经验风险损失项).

多层感知机

神经网络/DL(也可加Φ(x))

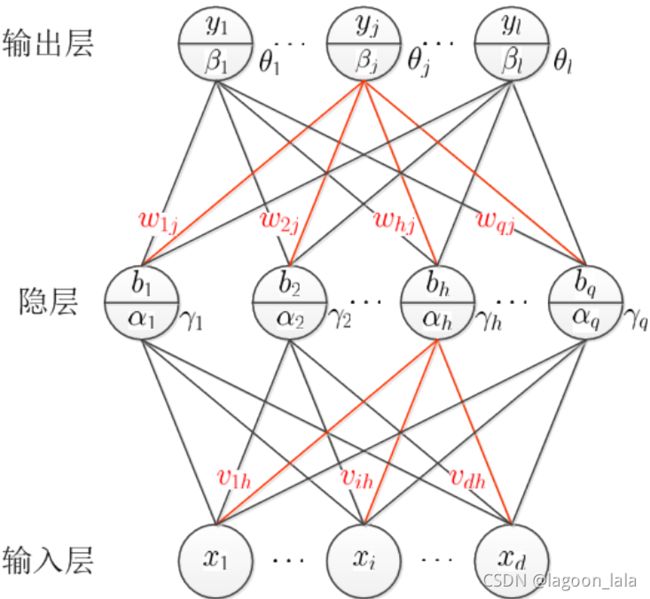
常见的神经网络为多层前馈神经网络 (multi-layer feedforward neural networks). 是层级结构，每层神经元与下层神经元全互连, 神经元之间不存在同层连接， 也不存在跨层连接. 其中, "前馈"指网络拓扑结构不存在环或回路.

训练多层网络，需要算法如BP(误差逆传播error BackPropagation) 算法进行训练. "BP 算法"可用于许多类型的神经网络, 但"BP 网络"指BP算法训练的多层前馈神经网络.

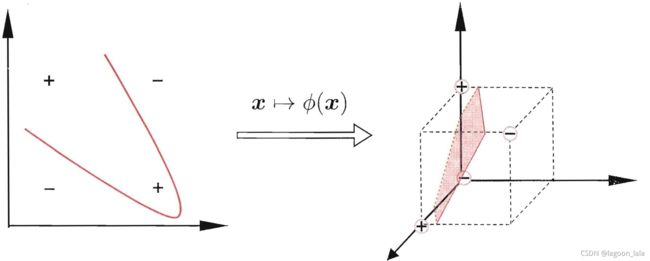
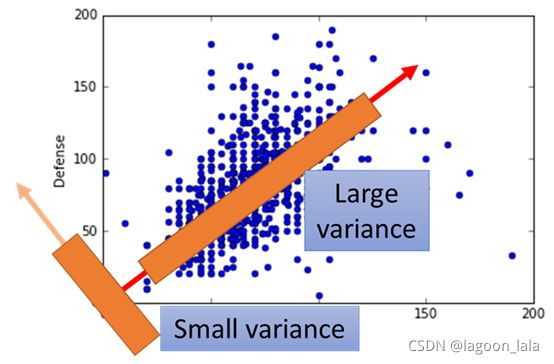
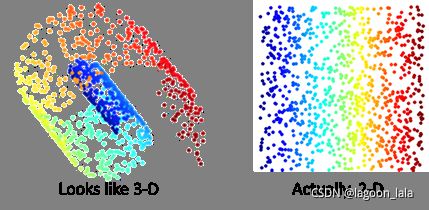
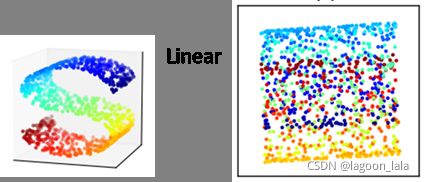
非线性映射

对于非线性可分问题(如'异或')映射到更高维的特征空间，使之线性可分.

Φ(x)表示映射后的特征向量

核函数

什么是核函数

可以写成映射Φ(x)的内积

Mercer 定理

任何半正定的函数都可以作为核函数

Every semi-positive definite symmetric function is a kernel

(充分不必要条件)

Mercer条件

若函数K(a, b)符合Mercer条件:

 K必须是连续的，并且在其参数上对称，所以K(a, b)=K(b, a),等等)，则存在函数φ将a和b映射到另一空间，使得K(a, b) = φ(a)T・φ(b)

解释了两个向量的核函数值等价于映射后的两个向量的内积

P150

Nystrom kernel可以用于用部分核信息来估计全体核信息。

 例子:

高斯核函数

1->2中间一项泰勒展开, 旁边两项为常数

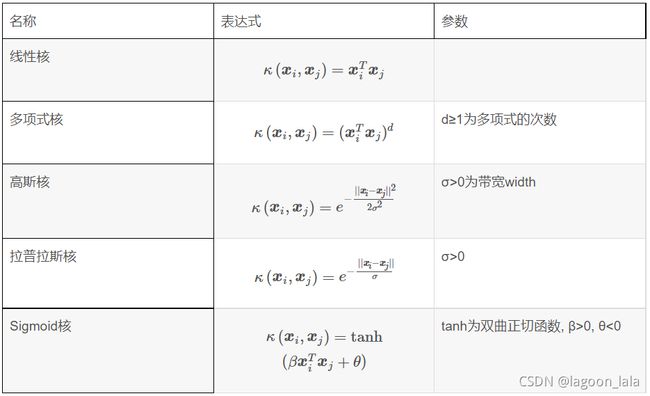
常用核函数:

高斯核灵活性最高, 带宽:

σ↑, 区分度↓欠拟合

σ↓, 区分度↑过拟合

如何使用核函数

核技巧Kernel Trick(计算

跳过求变换, 直接得到内积结果

一种φ对应的核函数(多项式核函数):

为什么要用核函数

核函数作用:

1. 模型角度: 非线性带来高维转换(Cover's Theorem)

数据: 低维->高维.

Cover's theorem，指的是对于非线性可分的训练集，可以大概率通过将其非线性映射到一个高维空间来转化成线性可分的训练集。

2. 优化角度: 对偶表示带来内积

映射后维度高, 对偶计算困难.

计算: 高维->低维

参考: https://blog.pluskid.org/?p=685&cpage=1#comment-4697

  

如何选择核函数

参考:

https://www.zhihu.com/question/21883548

kernel selection 近几年很火 可以关注相关工作 主要是给出准则 高效求解

RBF需要注意对数据归一化处理

很多核函数的经典问题

参考: https://blog.csdn.net/qq_34069667/article/details/106793766

因此，在选用核函数的时候，如果我们对我们的数据有一定的先验知识，就利用先验来选择符合数据分布的核函数；如果不知道的话，通常使用交叉验证的方法，来试用不同的核函数，误差最小的即为效果最好的核函数，或者也可以将多个核函数结合起来，形成混合核函数。

线性核

主要用于线性可分的情况，我们可以看到特征空间到输入空间的维度是一样的，其参数少速度快，对于线性可分数据，其分类效果很理想，因此我们通常首先尝试用线性核函数来做分类，看看效果如何，如果不行再换别的

linear kernel可以是RBF kernel的特殊情况

  

多项式核函数

多项式核函数可以实现将低维的输入空间映射到高纬的特征空间，但是参数多，当多项式的阶数比较高的时候，核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算

polynomial kernel的参数比RBF多，而参数越多模型越复杂. RBF kernel更方便计算，取值在[0,1]；而用polynomial kernel取值范围是(0,inf)，在自由度高的情况下更凸显出劣势

  

高斯（RBF）核函数

高斯径向基函数是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间内，该核函数是应用最广的一个，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少，因此大多数情况下在不知道用什么核函数的时候，优先使用高斯核函数。

在支持向量机(以下简称SVM)的核函数中，高斯核(以下简称RBF)是最常用的，从理论上讲， RBF一定不比线性核函数差，但是在实际应用中，却面临着几个重要的超参数的调优问题。如果调的不好，可能比线性核函数还要差。所以我们实际应用中，能用线性核函数得到较好效果的都会选择线性核函数。如果线性核不好，我们就需要使用RBF

一般用线性核和高斯核，也就是Linear核与RBF核，然后一般情况下RBF效果是不会差于Linear但是时间上RBF会耗费更多(因为核函数需要计算内积，两两样本都得算，所以样本过多的话时间消耗太大，很明显高斯核比线性核复杂的多, 且高斯核函数产生的特征比较多)

sigmoid核函数

sigmoid核函数支持向量机=神经网络的一种

RBF kernel可以处理非线性的情况，

linear kernel可以是RBF kernel的特殊情况，

sigmoid kernel又在某些参数下和RBF很像, 可能在某些参数下是无效的当然有些情况下用linear kernel就好了，比如特征维数很高的时候

MKL

 几类特征对应的最佳的核函数未必相同,让他们共用同一个核函数,未必能得到最优的映射。多核学习(MKL)属于后期融合的一种,通过对不同的特征采取不同的核,对不同的参数组成多个核,然后训练每个核的权重,选出最佳核函数组合

MKL有现成的code:

simpleMKL的作者放了。shogun工具包里面也有

(吴恩达:)

（1）特征维数很高，往往线性可分（SVM解决非线性分类问题的思路就是将样本映射到更高维的特征空间中），可以采用LR或者线性核的SVM；

（2）特征维度较小, 如果样本数量很多，由于求解最优化问题的时候，目标函数涉及两两样本计算内积，使用高斯核明显计算量会大于线性核，所以手动添加一些特征，使得线性可分，然后可以用LR或者线性核的SVM；

（3）不满足上述两点，即特征维数少，样本数量正常，使用高斯核的SVM。

	特征维数高	特征维数低
样本数量很多	线性可分, LR或线性核的SVM	手动添加特征, LR或线性核的SVM
样本数量正常		高斯核的SVM

核函数调参

SVM调参(附代码)

https://www.cnblogs.com/pinard/p/6126077.html

讲了各个参数的意义

最后还是用了网格搜索

调参代码(用自带数据集iris)

https://www.jianshu.com/p/55b9f2ea283b

蜥蜴书降维的调参:

(无监督, 无指标)

1. 可用(交叉验证的)网格搜索, 利用降维后续性能指标.

2. 选择重建误差最低的核和超参数. 在特征空间对已经降维的点进行逆转换, 原始空间与其对应点距离.

参数含义

当问题比较难时要试着把核宽度调大一些。

σ↑, 区分度↓欠拟合

σ↓, 区分度↑过拟合

若linear核比rbf核好，试试如下策略:

1. 降低gamma数值，能得到和linear核相似的性能。

2. rbf核对特征数值敏感，试着对特征做一些归一化，或者把数值缩放(例如libsvm中的svm-scale)试试。

RBF参数含义参考:

https://blog.csdn.net/wn314/article/details/79972988

惩罚系数C和RBF核函数的系数γ

惩罚系数C

即松弛变量的系数。在优化函数里平衡模型的复杂度和误分类率这两者之间的关系，可以理解为正则化系数。

软间隔优化函数:

scikit-learn中默认值是1。

在误分类样本和分界面简单性之间进行权衡。低的C值使分界面平滑，而高的C值通过增加模型自由度以选择更多支持向量来确保所有样本都被正确分类。

对mis classification 的惩罚度，惩罚越大，margin越窄，support vector 越少，但是这样会不robust，也就是稍微变动一下，separating hyperplane 就变很多。

惩罚度小，则反之。

当C比较大时，损失函数也会越大，不愿意放弃比较远的离群点。这样我们会有比较少的支持向量，也就是说支持向量和超平面的模型也会变得越复杂，也容易过拟合。

反之，当CC比较小时，对离群点不敏感，会选择较多的样本来做支持向量，最终的支持向量和超平面的模型也会简单。

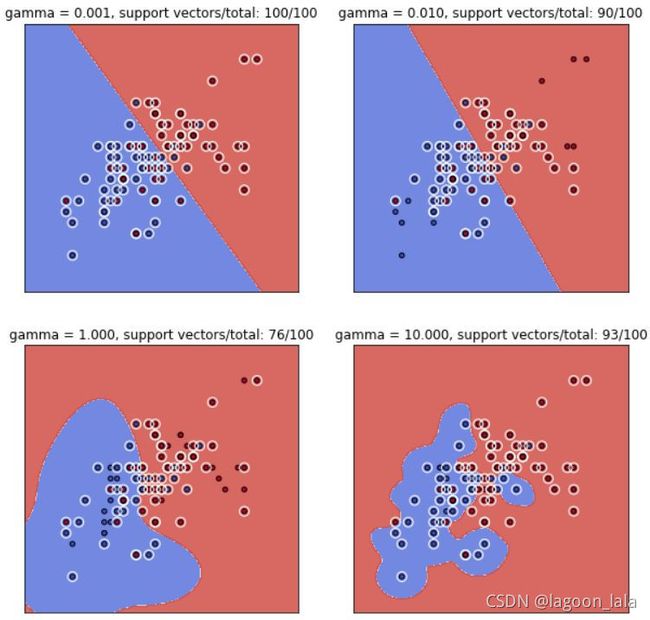
RBF核函数的参数γ

RBF 核函数:

  

参数gamma定义了单个训练样本的影响大小，值越小影响越大，值越大影响越小。参数gamma可以看作被模型选中作为支持向量的样本的影响半径的倒数。

当γ比较小时，单个样本对整个分类超平面的影响距离比较远，容易被选择为支持向量，

当γ比较大时，单个样本对整个分类超平面的影响距离比较近，不容易被选择为支持向量，整个模型的支持向量也会少，模型会变得更复杂。

scikit-learn中默认值是1/Dim(即样本特征数)

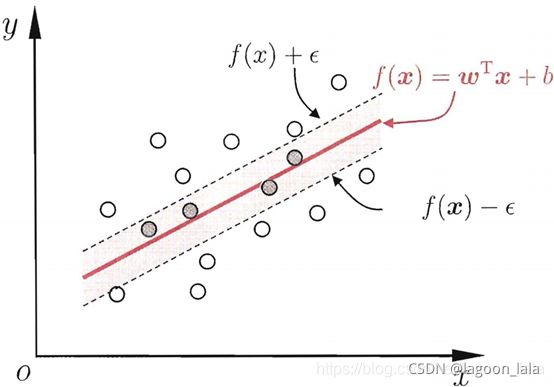
损失距离度量ϵ

SVR时用, 当f(x)与y差别绝对值大于ϵ 计算损失. 它决定了样本点到超平面的距离损失，当ϵ比较大时，损失较小，更多的点在损失距离范围之内，而没有损失,模型较简单，而当ϵϵ比较小时，损失函数会较大，模型也会变得复杂。scikit-learn中默认值是0.1。

如果把惩罚系数CC，RBF核函数的系数γγ和损失距离度量ϵϵ一起看，当CC比较大， γγ比较大，ϵϵ比较小时，我们会有更少的支持向量，我们的模型会比较复杂，容易过拟合一些。如果CC比较小 ， γγ比较小，ϵϵ比较大时，模型会变得简单，支持向量的个数会多。

支持向量数目对模型的影响, 参考:

https://www.zhihu.com/question/267666488/answer/347728105

grid search

网格搜索法是指定参数值的一种穷举搜索方法，通过将估计函数的参数通过交叉验证的方法进行优化来得到最优的学习算法。

即，将各个参数可能的取值进行排列组合，列出所有可能的组合结果生成“网格”。然后将各组合用于SVM训练，并使用交叉验证对表现进行评估。在拟合函数尝试了所有的参数组合后，返回一个合适的分类器，自动调整至最佳参数组合，可以通过clf.best_params_获得参数值

网格搜索缺点

Grid Search 调参方法存在的共性弊端就是：耗时；参数越多，候选值越多，耗费时间越长！所以，一般情况下，先定一个大范围，然后再细化。

在 sklearn 中可以用 grid search 找到合适的 kernel，以及它们的 gamma，C 等参数.

其中有两个重要的参数，即 C（惩罚系数） 和 gamma，

gamma 越大，支持向量越少，gamma 越小，支持向量越多。

而支持向量的个数影响训练和预测的速度。

C 越高，容易过拟合。C 越小，容易欠拟合。

自动算法，可以尝试，不是很靠谱。靠谱的还是grid search。

grid.py寻找最优参数C和g，这时候默认用的是RBF核

g 就是 RBF 核里的参数 gamma，所以是 RBF 核。大部分代码，都是交叉验证来寻找 RBF 核的参数，因为这个核的性能较好，对参数的依赖性也非常大。

如果是线性核或其它核，可以自己写个程序，即计算参数取不同值的时候，交叉验证的结果，然后选择最优结果对应的参数。

多参数调参可以用控制变量法，先调整一个参数，固定其它所有参数，挑选某值使结果相对最优。再固定该参数，改变其它某个参数，观察结果选择最优参数。

调参编程实现

调参代码(用自带数据集iris)

https://www.jianshu.com/p/55b9f2ea283b

from sklearn.datasets import load_iris from sklearn.svm import SVC from sklearn.model_selection import train_test_split iris = load_iris() X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=0) print("Size of training set:{} size of testing set:{}".format(X_train.shape[0],X_test.shape[0])) ####   grid search start best_score = 0 for gamma in [0.001,0.01,0.1,1,10,100]:     for C in [0.001,0.01,0.1,1,10,100]:         svm = SVC(gamma=gamma,C=C)#对于每种参数可能的组合，进行一次训练；         svm.fit(X_train,y_train)         score = svm.score(X_test,y_test)         if score > best_score:#找到表现最好的参数             best_score = score             best_parameters = {'gamma':gamma,'C':C} ####   grid search end print("Best score:{:.2f}".format(best_score)) print("Best parameters:{}".format(best_parameters))

activate Liver cd /d D:\anacondaProject\SVM_grid_demo python grid_search.py

Size of training set:112 size of testing set:38 Best score:0.97 Best parameters:{'gamma': 0.001, 'C': 100}

其中score函数:

>>> help(SVC.score) Help on function score in module sklearn.base: score(self, X, y, sample_weight=None)     Return the mean accuracy on the given test data and labels.     In multi-label classification, this is the subset accuracy     which is a harsh metric since you require for each sample that     each label set be correctly predicted.     Parameters     ----------     X : array-like of shape (n_samples, n_features)         Test samples.     y : array-like of shape (n_samples,) or (n_samples, n_outputs)         True labels for X.     sample_weight : array-like of shape (n_samples,), default=None         Sample weights.     Returns     -------     score : float         Mean accuracy of self.predict(X) wrt. y

蜥蜴书代码:

http://github.com/ageron/handson-ml2

核⽅法

Kernel Method核⽅法

定义: 基于核函数的学习方法，统称为"核方法"

常用来通过线性分类方法求解非线性分类问题:

1.首先使用一个变换将原空间的数据映射到新空间;

2.然后在新空间里用线性分类学习方法从训练数据中学习分类模型。

常用符号

核化过程中常用变量含义

核矩阵

$$ \mathbf{K}=\left[\begin{array}{ccccc} \kappa\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{1}\right) & \cdots & \kappa\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{j}\right) & \cdots & \kappa\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{m}\right) \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ \kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{1}\right) & \cdots & \kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) & \cdots & \kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{m}\right) \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ \kappa\left(\boldsymbol{x}_{m}, \boldsymbol{x}_{1}\right) & \cdots & \kappa\left(\boldsymbol{x}_{m}, \boldsymbol{x}_{j}\right) & \cdots & \kappa\left(\boldsymbol{x}_{m}, \boldsymbol{x}_{m}\right) \end{array}\right] \\ \mathbf{K}_{i j}=\kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)$$

第i类样本数量
第i类样本集
第i类样本的指示向量, l_ij为第j个特征
第i类样本均值向量

例子:4个样本

KLDA

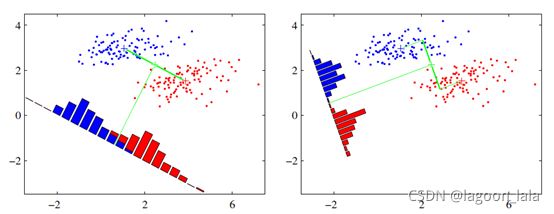
LDA的思想是：最大化类间均值，最小化类内方差

LDA: 监督学习的降维

核线性判别分析KLDA (Kernelized Linear Discriminant Analysis)

KLDA解形式对比LDA解形式(直线方程):

LDA学习目标(广义瑞利商)对比KLDA学习目标

其中S_b为类间散度, S_w为类内散度, 换了个特征空间.

模型核化

用核函数表达映射Φ则为投影函数(投影直线方程)

KLDA推导见SVM的核方法一节:

https://blog.csdn.net/lagoon_lala/article/details/118162845

SVM

划分超平面

原问题:

对偶问题:

KPCA

PCA无监督降维方法

最近重构性和最大可分性

用更少的维度表示, 且压缩后的数据方差最大

KPCA

现实常需要非线性映射才能找到恰当的低维嵌入

PCA: 丢弃新坐标系中的部分坐标

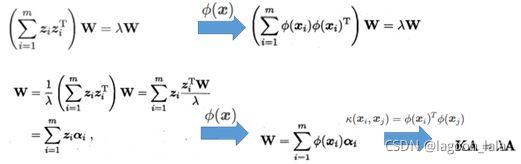
KPCA: 样本映射至高维特征空间, 再把数据x投影到超平面W

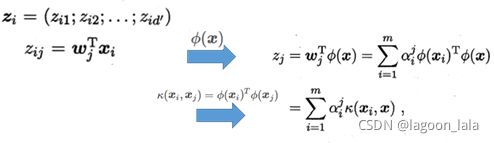
对比样本点xi在低维坐标系中的投影:

其中α为核函数κ线性组合的系数, 投影后坐标z:

$$ z_j=\sum_{i=1}^{m} \alpha_{i}^{j} \kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right) $$

PCA求解对比KPCA求解

其中λ为最大的dim个特征值, W为λ对应的特征向量.

推导参考:

https://datawhalechina.github.io/pumpkin-book/#/chapter10/chapter10?id=_1024

将公式中\(\phi(\boldsymbol{x}_{i})\)用\( \mathbf{Z} \)代入: $$ \left(\sum_{i=1}^{m} \phi(\boldsymbol{x}_{i}) \phi(\boldsymbol{x}_{i})^{\mathrm{T}}\right)\boldsymbol w_j=\left(\sum_{i=1}^{m} \boldsymbol z_i \boldsymbol z_i^{\mathrm{T}}\right)\boldsymbol w_j=\mathbf{Z}\mathbf{Z}^{\mathrm{T}}\boldsymbol w_j=\lambda_j\boldsymbol w_j $$ $$ \boldsymbol w_j=\sum_{i=1}^{m} \phi\left(\boldsymbol{x}_{i}\right) \alpha_{i}^j=\sum_{i=1}^{m} \boldsymbol z_i \alpha_{i}^j=\mathbf{Z}\boldsymbol{\alpha}^j $$ 联立两式, 式1两边的w分别代入式2, 得: $$ \begin{aligned} \mathbf{Z}\mathbf{Z}^{\mathrm{T}}\mathbf{Z}\boldsymbol{\alpha}^j&=\lambda_j\mathbf{Z}\boldsymbol{\alpha}^j \\ \mathbf{Z}\mathbf{Z}^{\mathrm{T}}\mathbf{Z}\boldsymbol{\alpha}^j&=\mathbf{Z}\lambda_j\boldsymbol{\alpha}^j \end{aligned} $$ $$ \mathbf{Z}^{\mathrm{T}}\mathbf{Z}\boldsymbol{\alpha}^j=\lambda_j\boldsymbol{\alpha}^j $$ 根据核方法: \( \mathbf{Z}^{\mathrm{T}}\mathbf{Z}=\mathbf{K} \) 得: $$ \mathbf{K}\boldsymbol{\alpha}^j=\lambda_j\boldsymbol{\alpha}^j $$ 此式即为特征值分解的形式: 得到了α, 就可根据公式w=αφ求得变换矩阵w, 也就可以求得新样本的坐标. 用核方法代入新样本坐标求解公式即为: $$ \begin{aligned} z_{j} &=\boldsymbol{w}_{j}^{\mathrm{T}} \phi(\boldsymbol{x})=\sum_{i=1}^{m} \alpha_{i}^{j} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}} \phi(\boldsymbol{x}) \\ &=\sum_{i=1}^{m} \alpha_{i}^{j} \kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right) \end{aligned} $$

MMDE

MMD最大均值差异(maximum mean discrepancy)

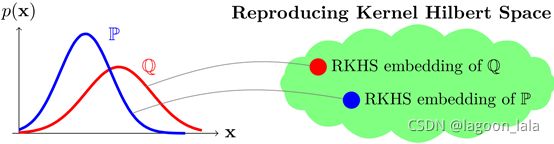
度量两个分布之间的距离

通过核函数, 将一个分布映射到再生希尔伯特空间（每个核函数都对应一个RKHS）上的一个点，这样两个分布之间的距离就可以用两个点的内积进行表示

先求一个分布的期望, 待会再看两个差异

随机变量经过映射φ(x)之后的期望:

核的可再生性(reproducing)，即用核函数来再生两个函数的内积。

第一个等号就是利用期望展开；第二个等号利用的是RKHS的再生性，即RKHS中的φ(x)都可以写成一个无穷维的向量k(x, ·)与基底向量φ的内积；第三个等号利用的是内积的性质；最后一个等号μ表示的就是kernel mean embedding.

即将x利用k(x, ·)映射到无穷维上，然后在每一个维度上都求期望.

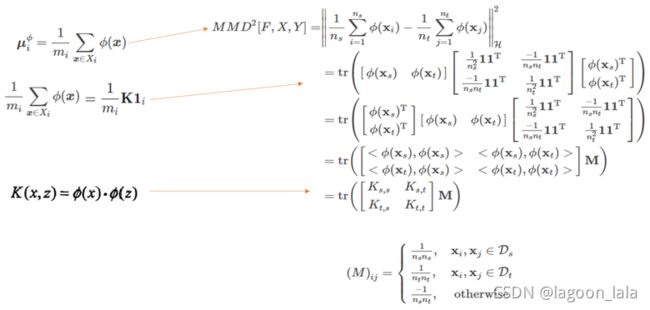
其中μ无法直接得到，但是可以用均值(均值是期望的无偏估计)替代计算(假设X样本n个, Y样本m个)

接下来MMD化为计算均值

对MMD平方后化简得到内积, 并代入核函数

这里的均值1/n*ΣΦ(x_i)其实就是前文提到的样本均值向量μ的估计