各种聚类算法的介绍与比较（转载）

转载自：https://blog.csdn.net/abc200941410128/article/details/78541273

一、简要介绍

聚类概念

聚类就是按照某个特定标准(如距离准则)把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。即聚类后同一类的数据尽可能聚集到一起，不同数据尽量分离。

聚类和分类的区别

聚类技术通常又被称为无监督学习，因为与监督学习不同，在聚类中那些表示数据类别的分类或者分组信息是没有的。
Clustering (聚类)，简单地说就是把相似的东西分到一组，聚类的时候，我们并不关心某一类是什么，我们需要实现的目标只是把相似的东西聚到一起。因此，一个聚类算法通常只需要知道如何计算相似度就可以开始工作了，因此 clustering 通常并不需要使用训练数据进行学习，这在Machine Learning中被称作unsupervised learning (无监督学习)。
Classification (分类)，对于一个classifier，通常需要你告诉它“这个东西被分为某某类”这样一些例子，理想情况下，一个 classifier 会从它得到的训练集中进行“学习”，从而具备对未知数据进行分类的能力，这种提供训练数据的过程通常叫做supervised learning (监督学习)。

衡量聚类算法优劣的标准

不同聚类算法有不同的优劣和不同的适用条件。大致上从跟数据的属性（是否序列输入、维度），算法模型的预设，模型的处理能力上看。具体如下：
1、算法的处理能力：处理大的数据集的能力（即算法复杂度）；处理数据噪声的能力；处理任意形状，包括有间隙的嵌套的数据的能力；
2、算法是否需要预设条件：是否需要预先知道聚类个数，是否需要用户给出领域知识；
3、算法的数据输入属性：算法处理的结果与数据输入的顺序是否相关，也就是说算法是否独立于数据输入顺序；算法处理有很多属性数据的能力，也就是对数据维数是否敏感，对数据的类型有无要求。

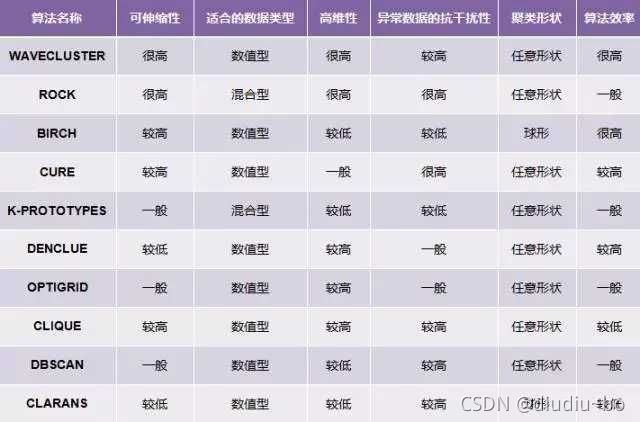
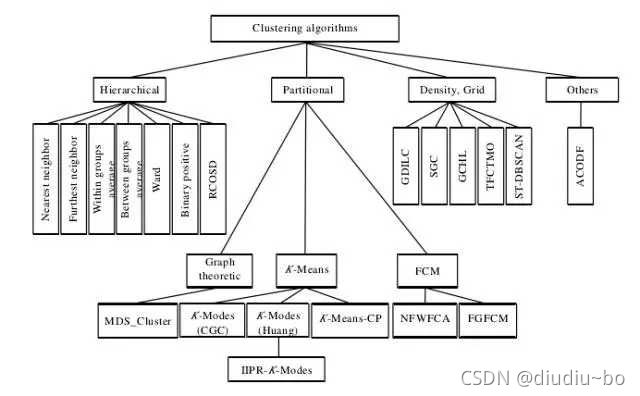
聚类算法有哪些类

算法介绍

基于层次的方法（Hierarchical methods）

基本思想

层次聚类主要有两种类型：合并的层次聚类和分裂的层次聚类。前者是一种自底向上的层次聚类算法，从最底层开始，每一次通过合并最相似的聚类来形成上一层次中的聚类，整个当全部数据点都合并到一个聚类的时候停止或者达到某个终止条件而结束，大部分层次聚类都是采用这种方法处理。后者是采用自顶向下的方法，从一个包含全部数据点的聚类开始，然后把根节点分裂为一些子聚类，每个子聚类再递归地继续往下分裂，直到出现只包含一个数据点的单节点聚类出现，即每个聚类中仅包含一个数据点。

算法流程

以下流程以自下向上为例。

1. 将每个对象看作一类，计算两两之间的最小距离；
2. 将距离最小的两个类合并成一个新类；
3. 重新计算新类与所有类之间的距离；
4. 重复2、3，直到所有类最后合并成一类

算法优缺点

优点：可解释性好（如当需要创建一种分类法时）；还有些研究表明这些算法能产生高质量的聚类，也会应用在上面说的先取K比较大的K-means后的合并阶段；还有对于K-means不能解决的非球形族就可以解决了。
缺点：时间复杂度高啊，o(m3)，改进后的算法也有o(m2lgm)，m为点的个数；贪心算法的缺点，一步错步步错；同K-means，difficulty handling different sized clusters and convex shapes。

常见的算法及改进

该聚类算法因为计算复杂度比较大适用于小数量级，如对中国省会城市聚类。改进的算法有BIRCH（Balanced Iterative Reducing and Clustering Using Hierarchies）主要是在数据体量很大的时候使用，而且数据类型是numerical。
Chameleon（A Hierarchical Clustering Algorithm Using Dynamic Modeling）里用到的linkage是kNN（k-nearest-neighbor）算法，并以此构建一个graph，Chameleon的聚类效果被认为非常强大，比BIRCH好用，但运算复杂还是很高，O(n^2)。看个Chameleon的聚类效果图，其中一个颜色代表一类，可以看出来是可以处理非常复杂的形状的。

基于划分的方法（Partition-based methods）

基本思想

基于划分的方法：其原理简单来说就是，想象你有一堆散点需要聚类，想要的聚类效果就是“类内的点都足够近，类间的点都足够远”。首先你要确定这堆散点最后聚成几类，然后挑选几个点作为初始中心点，再然后依据预先定好的启发式算法（heuristic algorithms）给数据点做迭代重置（iterative relocation），直到最后到达“类内的点都足够近，类间的点都足够远”的目标效果。也正是根据所谓的“启发式算法”，形成了k-means算法及其变体包括k-medoids、k-modes、k-medians、kernel k-means等算法。

算法流程

经典K-means算法流程：

1. 随机地选择k个对象，每个对象初始地代表了一个簇的中心；
2. 对剩余的每个对象，根据其与各簇中心的距离，将它赋给最近的簇；
3. 重新计算每个簇的平均值，更新为新的簇中心；
4. 不断重复2、3，直到准则函数收敛。

算法优缺点

优点：对于大型数据集也是简单高效、时间复杂度、空间复杂度低。
缺点：最重要是数据集大时结果容易局部最优；需要预先设定K值，对最先的K个点选取很敏感；对噪声和离群值非常敏感；只用于numerical类型数据；不能解决非凸（non-convex）数据。

常见的算法及改进

k-means对初始值的设置很敏感，所以有了k-means++、intelligent k-means、genetic k-means。
k-means对噪声和离群值非常敏感，所以有了k-medoids和k-medians。
k-means只用于numerical类型数据，不适用于categorical类型数据，所以k-modes。
k-means不能解决非凸（non-convex）数据，所以有了kernel k-means。
另外，很多教程都告诉我们Partition-based methods聚类多适用于中等体量的数据集，但我们也不知道“中等”到底有多“中”，所以不妨理解成，数据集越大，越有可能陷入局部最小。下图显示的就是面对非凸，k-means和kernel k-means的不同效果。

基于密度的方法(Density-based methods)

基本思想

基于密度的方法：k-means解决不了不规则形状的聚类。于是就有了Density-based methods来系统解决这个问题。该方法同时也对噪声数据的处理比较好。其原理简单说画圈儿，其中要定义两个参数，一个是圈儿的最大半径，一个是一个圈儿里最少应容纳几个点。只要邻近区域的密度（对象或数据点的数目）超过某个阈值，就继续聚类,最后在一个圈里的，就是一个类。DBSCAN（Density-Based Spatial Clustering of Applications with Noise）就是其中的典型.

算法流程

DBSCAN流程：

1. 从任一对象点p开始；
2. 寻找并合并核心p对象直接密度可达（eps）的对象；
3. 如果p是一个核心点，则找到了一个聚类，如果p是一个边界点（即从p没有密度可达的点）则寻找下一个对象点；
4. 重复2、3，直到所有点都被处理

DBSCAN聚类算法原理的基本要点：确定半径eps的值
①DBSCAN算法需要选择一种距离度量，对于待聚类的数据集中，任意两个点之间的距离，反映了点之间的密度，说明了点与点是否能够聚到同一类中。由于DBSCAN算法对高维数据定义密度很困难，所以对于二维空间中的点，可以使用欧几里德距离来进行度量。
②DBSCAN算法需要用户输入2个参数：一个是半径（Eps），表示以给定点P为中心的圆形邻域的范围；另一个是以点P为中心的邻域内最少点的数量（MinPts）。如果满足：以点P为中心、半径为Eps的邻域内的点的个数不少于MinPts，则称点P为核心点。
③DBSCAN聚类使用到一个k-距离的概念，k-距离是指：给定数据集P={p(i);i=0,1,…n}，对于任意点P(i)，计算点P(i)到集合D的子集S={p(1), p(2), …, p(i-1), p(i+1), …, p(n)}中所有点之间的距离，距离按照从小到大的顺序排序，假设排序后的距离集合为D={d(1), d(2), …, d(k-1), d(k), d(k+1),…,d(n)}，则d(k)就被称为k-距离。也就是说，k-距离是点p(i)到所有点（除了p(i)点）之间距离第k近的距离。对待聚类集合中每个点p(i)都计算k-距离，最后得到所有点的k-距离集合E={e(1), e(2), …, e(n)}。
④根据经验计算半径Eps：根据得到的所有点的k-距离集合E，对集合E进行升序排序后得到k-距离集合E’，需要拟合一条排序后的E’集合中k-距离的变化曲线图，然后绘出曲线，通过观察，将急剧发生变化的位置所对应的k-距离的值，确定为半径Eps的值。
⑤根据经验计算最少点的数量MinPts：确定MinPts的大小，实际上也是确定k-距离中k的值，DBSCAN算法取k=4，则MinPts=4。
⑥如果对经验值聚类的结果不满意，可以适当调整Eps和MinPts的值，经过多次迭代计算对比，选择最合适的参数值。可以看出，如果MinPts不变，Eps取得值过大，会导致大多数点都聚到同一个簇中，Eps过小，会导致一个簇的分裂；如果Eps不变，MinPts的值取得过大，会导致同一个簇中点被标记为噪声点，MinPts过小，会导致发现大量的核心点。
我们需要知道的是，DBSCAN算法，需要输入2个参数，这两个参数的计算都来自经验知识。半径Eps的计算依赖于计算k-距离，DBSCAN取k=4，也就是设置MinPts=4，然后需要根据k-距离曲线，根据经验观察找到合适的半径Eps的值。

算法优缺点

优点：对噪声不敏感；能发现任意形状的聚类。
缺点：聚类的结果与参数有很大的关系；DBSCAN用固定参数识别聚类，但当聚类的稀疏程度不同时，相同的判定标准可能会破坏聚类的自然结构，即较稀的聚类会被划分为多个类或密度较大且离得较近的类会被合并成一个聚类。

常见的算法及改进

DBSCAN对这两个参数的设置非常敏感。DBSCAN的扩展叫OPTICS（Ordering Points To Identify Clustering Structure）通过优先对高密度（high density）进行搜索，然后根据高密度的特点设置参数，改善了DBSCAN的不足。下图就是表现了DBSCAN对参数设置的敏感，你们可以感受下。

基于网络的方法（Grid-based methods）

基本思想

基于网络的方法：这类方法的原理就是将数据空间划分为网格单元，将数据对象集映射到网格单元中，并计算每个单元的密度。根据预设的阈值判断每个网格单元是否为高密度单元，由邻近的稠密单元组形成”类“。

算法流程

这些算法用不同的网格划分方法，将数据空间划分成为有限个单元（cell）的网格结构,并对网格数据结构进行了不同的处理，但核心步骤是相同的：
1、 划分网格
2、 使用网格单元内数据的统计信息对数据进行压缩表达
3、 基于这些统计信息判断高密度网格单元
4、 最后将相连的高密度网格单元识别为簇

算法优缺点

优点：速度很快，因为其速度与数据对象的个数无关，而只依赖于数据空间中每个维上单元的个数。
缺点：参数敏感、无法处理不规则分布的数据、维数灾难等；这种算法效率的提高是以聚类结果的精确性为代价的。经常与基于密度的算法结合使用。

常见的算法及改进

STING（STatistical INformation Grid）算法、WAVE-CLUSTER算法和CLIQUE（CLustering In QUEst）是该类方法中的代表性算法。下图是CLIQUE的一个例子：

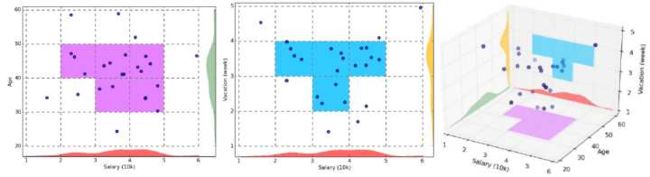
基于模型的方法（Model-based methods）

基本思想

基于模型的方法：为每簇假定了一个模型，寻找数据对给定模型的最佳拟合，这一类方法主要是指基于概率模型的方法和基于神经网络模型的方法，尤其以基于概率模型的方法居多。这里的概率模型主要指概率生成模型（generative Model），同一”类“的数据属于同一种概率分布，即假设数据是根据潜在的概率分布生成的。其中最典型、也最常用的方法就是高斯混合模型（GMM，Gaussian Mixture Models）。基于神经网络模型的方法主要就是指SOM（Self Organized Maps）了，也是我所知的唯一一个非监督学习的神经网络了。下图表现的就是GMM的一个demo，里面用到EM算法来做最大似然估计。

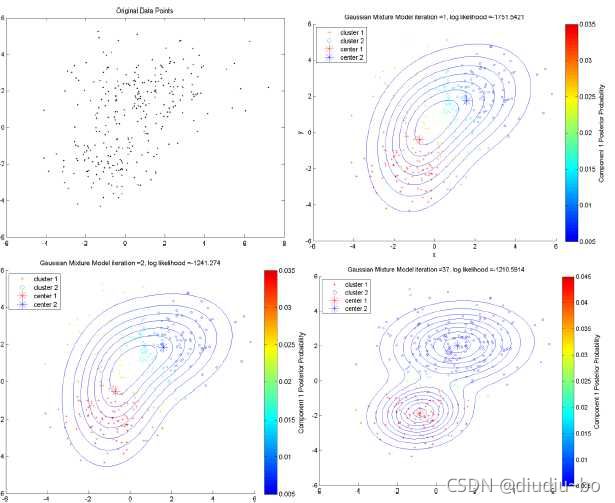
算法流程

【以SOM为例】SOM神经网络是由芬兰神经网络专家Kohonen教授提出的，该算法假设在输入对象中存在一些拓扑结构或顺序，可以实现从输入空间(n维)到输出平面(2维)的降维映射，其映射具有拓扑特征保持性质,与实际的大脑处理有很强的理论联系。
SOM网络包含输入层和输出层。输入层对应一个高维的输入向量，输出层由一系列组织在2维网格上的有序节点构成，输入节点与输出节点通过权重向量连接。学习过程中，找到与之距离最短的输出层单元，即获胜单元，对其更新。同时，将邻近区域的权值更新，使输出节点保持输入向量的拓扑特征。
算法流程：
1、 网络初始化，对输出层每个节点权重赋初值；
2、 将输入样本中随机选取输入向量，找到与输入向量距离最小的权重向量；
3、定义获胜单元，在获胜单元的邻近区域调整权重使其向输入向量靠拢；
4、 提供新样本、进行训练；
5、收缩邻域半径、减小学习率、重复，直到小于允许值，输出聚类结果。

算法优缺点

优点：对”类“的划分不那么”坚硬“，而是以概率形式表现，每一类的特征也可以用参数来表达。
缺点：执行效率不高，特别是分布数量很多并且数据量很少的时候。

常见的算法及改进

基于概率模型的最典型、也最常用的方法就是高斯混合模型（GMM，Gaussian Mixture Models）。基于神经网络模型的方法主要就是指SOM（Self Organized Maps）了，也是我所知的唯一一个非监督学习的神经网络了。

基于模糊的聚类（FCM模糊聚类）

基本思想

1965年美国加州大学柏克莱分校的扎德教授第一次提出了‘集合’的概念。经过十多年的发展，模糊集合理论渐渐被应用到各个实际应用方面。为克服非此即彼的分类缺点，出现了以模糊集合论为数学基础的聚类分析。用模糊数学的方法进行聚类分析，就是模糊聚类分析。
基于模糊集理论的聚类方法，样本以一定的概率属于某个类。比较典型的有基于目标函数的模糊聚类方法、基于相似性关系和模糊关系的方法、基于模糊等价关系的传递闭包方法、基于模 糊图论的最小支撑树方法，以及基于数据集的凸分解、动态规划和难以辨别关系等方法。FCM算法是一种以隶属度来确定每个数据点属于某个聚类程度的算法。该聚类算法是传统硬聚类算法的一种改进。

算法流程

FCM模糊聚类算法流程：
1、 标准化数据矩阵；
2、 建立模糊相似矩阵，初始化隶属矩阵；
3、 算法开始迭代，直到目标函数收敛到极小值；
4、 根据迭代结果，由最后的隶属矩阵确定数据所属的类，显示最后的聚类结果。
FCM算法需要两个参数一个是聚类数目C，另一个是参数m。一般来讲C要远远小于聚类样本的总个数，同时要保证C>1。对于m，它是一个控制算法的柔性的参数，如果m过大，则聚类效果会很次，而如果m过小则算法会接近HCM聚类算法。
算法的输出是C个聚类中心点向量和C*N的一个模糊划分矩阵，这个矩阵表示的是每个样本点属于每个类的隶属度。根据这个划分矩阵按照模糊集合中的最大隶属原则就能够确定每个样本点归为哪个类。聚类中心表示的是每个类的平均特征，可以认为是这个类的代表点。

算法优缺点

优点：从算法的推导过程中我们不难看出，算法对于满足正态分布的数据聚类效果会很好，另外，算法对孤立点是敏感的。
缺点：由于不能确保FCM收敛于一个最优解。算法的性能依赖于初始聚类中心。因此，我们要么用另外的快速算法确定初始聚类中心，要么每次用不同的初始聚类中心启动该算法，多次运行FCM。

常见的算法及改进

模糊C均值（简称FCM）聚类算法是HCM聚类算法的改进。

其他聚类

除此以外还有一些其他新的发展方法，在此只简要介绍。

基于约束的方法

真实世界中的聚类问题往往是具备多种约束条件的 , 然而由于在处理过程中不能准确表达相应的约束条件、不能很好地利用约束知识进行推理以及不能有效利用动态的约束条件 , 使得这一方法无法得到广泛的推广和应用。这里的约束可以是对个体对象的约束 , 也可以是对聚类参数的约束 , 它们均来自相关领域的经验知识。该方法的一个重要应用在于对存在障碍数据的二维空间数据进行聚类。 COD (Clustering with Ob2structed Distance) 就是处理这类问题的典型算法 , 其主要思想是用两点之间的障碍距离取代了一般的欧氏距离来计算其间的最小距离。

量子聚类：

受物理学中量子机理和特性启发，可以用量子理论解决聚类记过依赖于初值和需要指定类别数的问题。一个很好的例子就是基于相关点的 Pott 自旋和统计机理提出的量子聚类模型。它把聚类问题看做一个物理系统。并且许多算例表明，对于传统聚类算法无能为力的几种聚类问题，该算法都得到了比较满意的结果。

核聚类

核聚类方法增加了对样本特征的优化过程，利用 Mercer 核 把输入空间的样本映射到高维特征空间，并在特征空间中进行聚类。核聚类方法是普适的，并在性能上优于经典的聚类算法，它通过非线性映射能够较好地分辨、提 取并放大有用的特征，从而实现更为准确的聚类；同时，算法的收敛速度也较快。在经典聚类算法失效的情况下，核聚类算法仍能够得到正确的聚类。代表算法有SVDD算法，SVC算法。

谱聚类

首先根据给定的样本数据集定义一个描述成对数据点相似度的亲合矩阵,并计算矩阵的特征值和特征向量,然后选择合适的特征向量聚类不同的数据点。谱聚类算法最初用于计算机视觉、VLSI设计等领域,最近才开始用于机器学习中,并迅速成为国际上机器学习领域的研究热点。
谱聚类算法建立在图论中的谱图理论基础上,其本质是将聚类问题转化为图的最优划分问题,是一种点对聚类算法。

方法扩展

数据简化方法

其实上面提到的很多算法就是对数据做了简化，才得以具备处理大规模数据的能力，比如BIRCH。但其实你可以任意组合，所以理论上把数据简化的方法和上面提到的十几种聚类算法结合使用，可以有上百个算法了。
（1）变换（Data Transformation）：离散傅里叶变换（Discrete Fourier Transformation）可以提取数据的频域（frequency domain）信息，离散小波变换（Discrete Wavelet Transformation）除了频域之外，还可以提取到时域（temporal domain）信息。
（2）降维（Dimensionality Reduction）：在降维的方法中，PCA（Principle Component Analysis）和SVD（Singular Value Decomposition）作为线性方法，受到最广泛的应用。还有像MDS（Multi-Dimensional Scaling）什么的，不过只是作为PCA的一个扩展，给我的感觉是中看不中用。这几个方法局限肯定是无法处理非线性特征明显的数据。处理非线性降维的算法主要是流形学习（Manifold Learning），这又是一大块内容，里面集中常见的算法包括ISOMAP、LLE（Locally Linear Embedding）、MVU（Maximum variance unfolding）、Laplacian eigenmaps、Hessian eigenmaps、Kernel PCA、Probabilistic PCA等等。流形学习还是挺有趣的，而且一直在发展。关于降维在聚类中的应用，最著名的应该就是谱聚类（Spectral Clustering），就是先用Laplacian eigenmaps对数据降维（简单地说，就是先将数据转换成邻接矩阵或相似性矩阵，再转换成Laplacian矩阵，再对Laplacian矩阵进行特征分解，把最小的K个特征向量排列在一起），然后再使用k-means完成聚类。谱聚类是个很好的方法，效果通常比k-means好，计算复杂度还低，这都要归功于降维的作用。
（3）抽样（Sampling）：最常用的就是随机抽样（Random Sampling）咯，如果你的数据集特别大，随机抽样就越能显示出它的低复杂性所带来的好处。比如CLARA（Clustering LARge Applications）就是因为k-medoids应对不了大规模的数据集，所以采用sampling的方法。一般抽样法采用的不多。

相似性衡量

前面提到聚类其实就是比较相似性的。（其实，本部分可能放到前面第一部分会好些。）
相似性衡量又可以细分为直接法和间接法（答主自己取的名字，求轻拍）：直接法是直接求取input data的相似性，间接法是求取data中提取出的features的相似性。但无论是求data还是feature的相似性，方法都是这么几种：
（1）距离。距离主要就是指Minkovski距离。这个名字虽然听起来陌生，但其算法就是Lp norm的算法，如果是L1 norm，那就是绝对值/曼哈顿距离（Manhattan distance）；如果是L2 norm，那就是著名的欧式距离（Euclidean distance）了，也是应用最广泛的；如果L无穷范式，supremum距离，好像也有叫切比雪夫距离的，但就很少有人用了。另外，还有Mahalanobis距离，目前来看主要应用于Gaussian Mixture Model（GMM），还有Lance&Williams距离等等，但几乎没见过求距离的时候会专门用这个的。
（2）相似系数。主要有夹角余弦和相关系数。相关系数的应用也非常广泛，其主要优势是它不受原线性变换的影响，而且可以轻松地转换为距离，但其运算速度要比距离法慢得多，当维数很高的时候。
（3）核函数K(x,y)。定义在R d X R d R^d X R^{d}R
d
XR
d
上的二元函数，本质上也是反映x和y的距离。核函数的功能就是把数据从低维空间投影（project）到高维空间去。
(4)DTW（dynamic time warping）。这是一种非常特殊的距离算法，它可以计算两个不同长度的向量的距离，也可以对两对向量中不同时间段内的数据做匹配。DTW主要用在时间序列的部分场合里。