NNDL 实验三 线性回归

2.2 线性回归

2.2.1 数据集构建

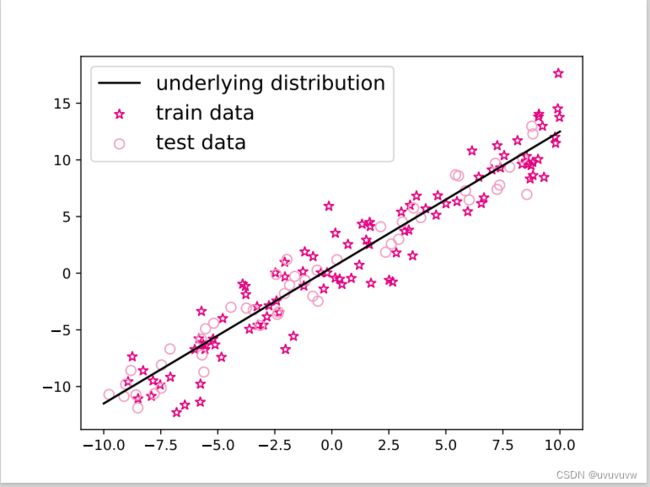
构造一个小的回归数据集：生成 150 个带噪音的样本，其中 100 个训练样本，50 个测试样本，并打印出训练数据的可视化分布。

代码如下:

# 真实函数的参数缺省值为 w=1.2，b=0.5
def linear_func(x, w=1.2, b=0.5):
    y = w * x + b
    return y


import os
import torch

os.environ["KMP_DUPLICATE_LIB_OK"] = 'TRUE'


def create_toy_data(func, interval, sample_num, noise=0.0, add_outlier=False, outlier_ratio=0.001):
    """
    根据给定的函数，生成样本
    输入：
       - func：函数
       - interval： x的取值范围
       - sample_num： 样本数目
       - noise： 噪声均方差
       - add_outlier：是否生成异常值
       - outlier_ratio：异常值占比
    输出：
       - X: 特征数据，shape=[n_samples,1]
       - y: 标签数据，shape=[n_samples,1]
    """

    # 均匀采样
    # 使用paddle.rand在生成sample_num个随机数
    X = torch.rand(sample_num) * (interval[1] - interval[0]) + interval[0]
    y = func(X)

    # 生成高斯分布的标签噪声
    # 使用torch.normal生成0均值，noise标准差的数据
    epsilon = torch.normal(0, noise, y.shape)
    y = y + epsilon
    if add_outlier:  # 生成额外的异常点
        outlier_num = int(len(y) * outlier_ratio)
        if outlier_num != 0:
            # 使用paddle.randint生成服从均匀分布的、范围在[0, len(y))的随机Tensor
            outlier_idx = torch.randint(len(y), [outlier_num])
            y[outlier_idx] = y[outlier_idx] * 5
    return X, y

利用上面的生成样本函数，生成 150 个带噪音的样本，其中 100 个训练样本，50 个测试样本，并打印出训练数据的可视化分布：

import torch
import matplotlib.pyplot as plt  # matplotlib 是 Python 的绘图库

func = linear_func
interval = (-10, 10)
train_num = 100  # 训练样本数目
test_num = 50  # 测试样本数目
noise = 2
X_train, y_train = create_toy_data(func=func, interval=interval, sample_num=train_num, noise=noise, add_outlier=False)
X_test, y_test = create_toy_data(func=func, interval=interval, sample_num=test_num, noise=noise, add_outlier=False)
X_train_large, y_train_large = create_toy_data(func=func, interval=interval, sample_num=5000, noise=noise,
                                               add_outlier=False)

# torch.linspace返回一个Tensor，Tensor的值为在区间start和stop上均匀间隔的num个值，输出Tensor的长度为num
X_underlying = torch.linspace(interval[0], interval[1], train_num)
y_underlying = linear_func(X_underlying)

# 绘制数据
plt.scatter(X_train, y_train, marker='*', facecolor="none", edgecolor='#e4007f', s=50, label="train data")
plt.scatter(X_test, y_test, facecolor="none", edgecolor='#f19ec2', s=50, label="test data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"underlying distribution")
plt.legend(fontsize='x-large')  # 给图像加图例
plt.savefig('ml-vis.pdf')  # 保存图像到PDF文件中
plt.show()

运行结果如下:

2.2.2 模型构建

在线性回归中，自变量为样本的特征向量(每一维对应一个自变量)，因变量是连续值的标签。

线性模型定义为：

其中权重向量和偏置都是可学习的参数。

注意：《神经网络与深度学习》中为了表示的简洁性，使用增广权重向量来定义模型。而在本书中，为了和代码实现保持一致，我们使用非增广向量的形式来定义模型。

在实践中，为了提高预测样本的效率，我们通常会将NN样本归为一组进行成批地预测，这样可以更好地利用GPU设备的并行计算能力。

其中为N个样本的特征矩阵，为N个预测值组成的列向量。

---

 

注意：在实践中，样本的矩阵X是由N个x的行向量组成。而原教材中x为列向量，其特征矩阵与本书中的特征矩阵刚好为转置关系。

2.2.2.1 线性算子

在pytorch框架中，可以直接调用模型的forward()方法进行前向执行，也可以调用__call__()，从而执行在 forward() 当中定义的前向计算逻辑。

在pytorch框架中，模型一般继承nn.Moudle，在成员函数forward()中执行模型的前向运算。由于本案例较简单，所以没有继承nn.Moudle，但是保留了在forward()函数中执行模型的前向运算的过程。

代码如下:

import numpy as np
import random
import torch

def setup_seed(seed):
    torch.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    np.random.seed(seed)
    random.seed(seed)
    torch.backends.cudnn.deterministic = True


# 设置随机数种子
setup_seed(10)


class Op(object):
    def __init__(self):
        pass

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        raise NotImplementedError

    def backward(self, inputs):
        raise NotImplementedError


# 线性算子
class Linear(Op):
    def __init__(self, input_size):
        """
        输入：
           - input_size:模型要处理的数据特征向量长度
        """

        super().__init__()
        self.input_size = input_size

        # 模型参数
        self.params = {}
        self.params['w'] = torch.randn([self.input_size, 1], dtype=torch.float32)
        self.params['b'] = torch.zeros([1], dtype=torch.float32)

    def __call__(self, X):
        return self.forward(X)

    # 前向函数
    def forward(self, X):
        """
        输入：
           - X: tensor, shape=[N,D]
           注意这里的X矩阵是由N个x向量的转置拼接成的，与原教材行向量表示方式不一致
        输出：
           - y_pred： tensor, shape=[N]
        """

        N, D = X.shape

        if self.input_size == 0:
            return torch.full([N, 1], self.params['b'])

        assert D == self.input_size  # 输入数据维度合法性验证

        # 使用paddle.matmul计算两个tensor的乘积
        y_pred = torch.matmul(X, self.params['w']) + self.params['b']

        return y_pred

测试代码:

input_size = 3
N = 2
X = torch.randn([N, input_size], dtype=torch.float32)  # 生成2个维度为3的数据
model = Linear(input_size)
y_pred = model(X)
print("y_pred:", y_pred)  # 输出结果的个数也是2个

运行结果如下:

y_pred: tensor([[1.8529],
        [0.6011]])

2.2.3 损失函数

回归任务是对连续值的预测，希望模型能根据数据的特征输出一个连续值作为预测值。因此回归任务中常用的评估指标是均方误差。

均方误差的代码实现如下:

def mean_squared_error(y_true, y_pred):
    """
    输入：
       - y_true: tensor，样本真实标签
       - y_pred: tensor, 样本预测标签
    输出：
       - error: float，误差值
    """

    assert y_true.shape[0] == y_pred.shape[0]

    # torch.square计算输入的平方值
    # torch.mean计算 x 的平均值，默认是None，则对输入的全部元素计算平均值。
    error = torch.mean(torch.square(y_true - y_pred))

    return error

构造一个简单的案例进行测试:

# 构造一个简单的样例进行测试:[N,1], N=2
y_true = torch.tensor([[-0.2], [4.9]], dtype=torch.float32)
y_pred = torch.tensor([[1.3], [2.5]], dtype=torch.float32)

error = mean_squared_error(y_true=y_true, y_pred=y_pred).item()
print("error:", error)

运行结果如下:

error: 4.005000114440918

2.2.4 模型优化

经验风险 （ Empirical Risk ），即在训练集上的平均损失。

实验代码如下:

def optimizer_lsm(model, X, y, reg_lambda=0):
    """
    输入：
       - model: 模型
       - X: tensor, 特征数据，shape=[N,D]
       - y: tensor,标签数据，shape=[N]
       - reg_lambda: float, 正则化系数，默认为0
    输出：
       - model: 优化好的模型
    """

    N, D = X.shape

    # 对输入特征数据所有特征向量求平均
    x_bar_tran = torch.mean(X, axis=0).T

    # 求标签的均值,shape=[1]
    y_bar = torch.mean(y)

    # paddle.subtract通过广播的方式实现矩阵减向量
    x_sub = torch.subtract(X, x_bar_tran)

    # 使用paddle.all判断输入tensor是否全0
    if torch.all(x_sub == 0):
        model.params['b'] = y_bar
        model.params['w'] = torch.zeros([D])
        return model

    # paddle.inverse求方阵的逆
    tmp = torch.inverse(torch.matmul(x_sub.T, x_sub) +
                        reg_lambda * torch.eye(D))

    w = torch.matmul(torch.matmul(tmp, x_sub.T), (y - y_bar))

    b = y_bar - torch.matmul(x_bar_tran, w)

    model.params['b'] = b
    model.params['w'] = torch.squeeze(w, axis=-1)

    return model

【思考】 为什么省略了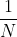不影响效果？

参数固定时，1/N只影响收敛速度，不影响结果

【思考】  什么是最小二乘法 （ Least Square Method ， LSM ）

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小

2.2.5 模型训练

在准备了数据、模型、损失函数和参数学习的实现之后，开始模型的训练。

在回归任务中，模型的评价指标和损失函数一致，都为均方误差。

通过上文实现的线性回归类来拟合训练数据，并输出模型在训练集上的损失。

代码如下:

input_size = 1
model = Linear(input_size)
model = optimizer_lsm(model,X_train.reshape([-1,1]),y_train.reshape([-1,1]))
print("w_pred:",model.params['w'].item(), "b_pred: ", model.params['b'].item())

y_train_pred = model(X_train.reshape([-1,1])).squeeze()
train_error = mean_squared_error(y_true=y_train, y_pred=y_train_pred).item()
print("train error: ",train_error)

model_large = Linear(input_size)
model_large = optimizer_lsm(model_large,X_train_large.reshape([-1,1]),y_train_large.reshape([-1,1]))
print("w_pred large:",model_large.params['w'].item(), "b_pred large: ", model_large.params['b'].item())

y_train_pred_large = model_large(X_train_large.reshape([-1,1])).squeeze()
train_error_large = mean_squared_error(y_true=y_train_large, y_pred=y_train_pred_large).item()
print("train error large: ",train_error_large)

运行结果如下:

 从输出结果看，预测结果与真实值w=1.2w=1.2，b=0.5b=0.5有一定的差距。

2.2.6 模型评估

下面用训练好的模型预测一下测试集的标签，并计算在测试集上的损失。

代码如下:

y_test_pred = model(X_test.reshape([-1, 1])).squeeze()
test_error = mean_squared_error(y_true=y_test, y_pred=y_test_pred).item()
print("test error: ", test_error)#

y_test_pred_large = model_large(X_test.reshape([-1,1])).squeeze()
test_error_large = mean_squared_error(y_true=y_test, y_pred=y_test_pred_large).item()
print("test error large: ",test_error_large)

测试结果如下:

2.2.7 样本数量 & 正则化系数

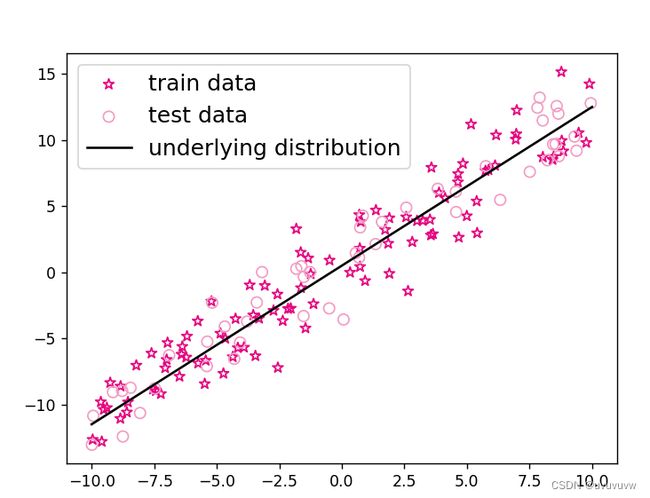
（1） 调整训练数据的样本数量，由 100 调整到 5000，观察对模型性能的影响。

将上面代码中

train_num = 100

改为

train_num = 5000

结果如下:

（2） 调整正则化系数，观察对模型性能的影响。

将reg_lambda从0改为0.1

结果:

2.3 多项式回归

2.3.1 数据集构建

构建训练和测试数据，其中：

训练数样本 15 个，测试样本 10 个，高斯噪声标准差为 0.1，自变量范围为 (0,1)。

import math
import torch
# sin函数: sin(2 * pi * x)
def sin(x):
    y = torch.sin(2 * math.pi * x)
    return y
# 生成数据
func = sin
interval = (0,1)
train_num = 15
test_num = 10
noise = 0.5 #0.1
X_train, y_train = create_toy_data(func=func, interval=interval, sample_num=train_num, noise = noise)
X_test, y_test = create_toy_data(func=func, interval=interval, sample_num=test_num, noise = noise)

X_underlying = torch.linspace(interval[0],interval[1],100)
y_underlying = sin(X_underlying)

# 绘制图像
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")
#plt.scatter(X_test, y_test, facecolor="none", edgecolor="r", s=50, label="test data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
plt.legend(fontsize='x-large')
plt.savefig('ml-vis2.pdf')
plt.show()

结果:

2.3.2 模型构建

通过多项式的定义可以看出，多项式回归和线性回归一样，同样学习参数ww，只不过需要对输入特征ϕ(x)ϕ(x)根据多项式阶数进行变换。因此，我们可以套用求解线性回归参数的方法来求解多项式回归参数。

# 多项式转换
import torch


def polynomial_basis_function(x, degree=2):
    """
    输入：
       - x: tensor, 输入的数据，shape=[N,1]
       - degree: int, 多项式的阶数
       example Input: [[2], [3], [4]], degree=2
       example Output: [[2^1, 2^2], [3^1, 3^2], [4^1, 4^2]]
       注意：本案例中,在degree>=1时不生成全为1的一列数据；degree为0时生成形状与输入相同，全1的Tensor
    输出：
       - x_result： tensor
    """

    if degree == 0:
        return torch.ones(shape=x.shape, dtype='float32')

    x_tmp = x
    x_result = x_tmp

    for i in range(2, degree + 1):
        x_tmp = torch.multiply(x_tmp, x)  # 逐元素相乘
        x_result = torch.concat((x_result, x_tmp), axis=-1)

    return x_result


# 简单测试
data = [[2], [3], [4]]
X = torch.tensor(data=data, dtype=torch.float32)
degree = 3
transformed_X = polynomial_basis_function(X, degree=degree)
print("转换前：", X)
print("阶数为", degree, "转换后：", transformed_X)

结果:

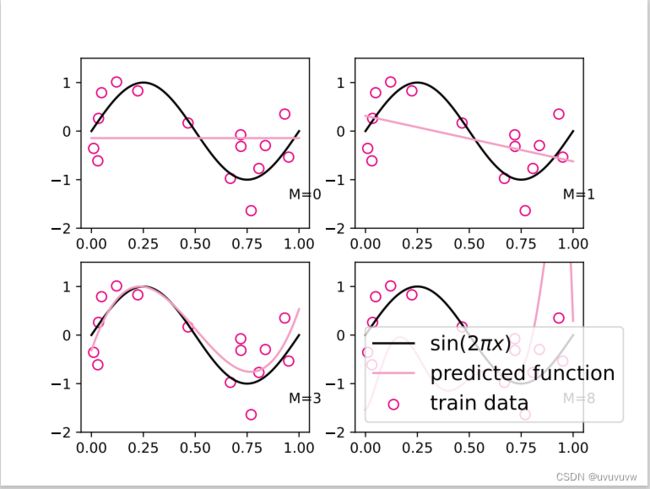
2.3.3 模型训练

对于多项式回归，我们可以同样使用前面线性回归中定义的LinearRegression算子、训练函数train、均方误差函数mean_squared_error。

plt.rcParams['figure.figsize'] = (12.0, 8.0)

for i, degree in enumerate([0, 1, 3, 8]):  # []中为多项式的阶数
    model = Linear(degree)
    X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), degree)
    X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), degree)

    model = optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1]))  # 拟合得到参数

    y_underlying_pred = model(X_underlying_transformed).squeeze()

    print(model.params)

    # 绘制图像
    plt.subplot(2, 2, i + 1)
    plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")
    plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
    plt.plot(X_underlying, y_underlying_pred, c='#f19ec2', label="predicted function")
    plt.ylim(-2, 1.5)
    plt.annotate("M={}".format(degree), xy=(0.95, -1.4))

# plt.legend(bbox_to_anchor=(1.05, 0.64), loc=2, borderaxespad=0.)
plt.legend(loc='lower left', fontsize='x-large')
plt.savefig('ml-vis3.pdf')
plt.show()

结果如下:

2.3.4 模型评估

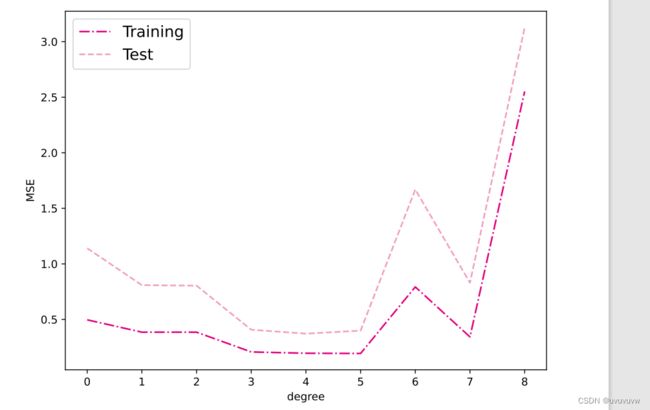
下面通过均方误差来衡量训练误差、测试误差以及在没有噪音的加入下sin函数值与多项式回归值之间的误差，更加真实地反映拟合结果。多项式分布阶数从0到8进行遍历。

# 训练误差和测试误差
training_errors = []
test_errors = []
distribution_errors = []

# 遍历多项式阶数
for i in range(9):
    model = Linear(i)

    X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), i)
    X_test_transformed = polynomial_basis_function(X_test.reshape([-1, 1]), i)
    X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), i)

    optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1]))

    y_train_pred = model(X_train_transformed).squeeze()
    y_test_pred = model(X_test_transformed).squeeze()
    y_underlying_pred = model(X_underlying_transformed).squeeze()

    train_mse = mean_squared_error(y_true=y_train, y_pred=y_train_pred).item()
    training_errors.append(train_mse)

    test_mse = mean_squared_error(y_true=y_test, y_pred=y_test_pred).item()
    test_errors.append(test_mse)

    # distribution_mse = mean_squared_error(y_true=y_underlying, y_pred=y_underlying_pred).item()
    # distribution_errors.append(distribution_mse)

print("train errors: \n", training_errors)
print("test errors: \n", test_errors)
# print ("distribution errors: \n", distribution_errors)

# 绘制图片
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.plot(training_errors, '-.', mfc="none", mec='#e4007f', ms=10, c='#e4007f', label="Training")
plt.plot(test_errors, '--', mfc="none", mec='#f19ec2', ms=10, c='#f19ec2', label="Test")
# plt.plot(distribution_errors, '-', mfc="none", mec="#3D3D3F", ms=10, c="#3D3D3F", label="Distribution")
plt.legend(fontsize='x-large')
plt.xlabel("degree")
plt.ylabel("MSE")
plt.savefig('ml-mse-error.pdf')
plt.show()

结果如下:

 可视化:

2.4 Runner类介绍

机器学习方法流程包括数据集构建、模型构建、损失函数定义、优化器、模型训练、模型评价、模型预测等环节。

为了更方便地将上述环节规范化，我们将机器学习模型的基本要素封装成一个Runner类。

除上述提到的要素外，再加上模型保存、模型加载等功能。

Runner类的成员函数定义如下：

• __init__函数：实例化Runner类，需要传入模型、损失函数、优化器和评价指标等；
• train函数：模型训练，指定模型训练需要的训练集和验证集；
• evaluate函数：通过对训练好的模型进行评价，在验证集或测试集上查看模型训练效果；
• predict函数：选取一条数据对训练好的模型进行预测；
• save_model函数：模型在训练过程和训练结束后需要进行保存；
• load_model函数：调用加载之前保存的模型。

2.5 基于线性回归的波士顿房价预测

使用线性回归来对马萨诸塞州波士顿郊区的房屋进行预测。

实验流程主要包含如下5个步骤：

• 数据处理：包括数据清洗（缺失值和异常值处理）、数据集划分，以便数据可以被模型正常读取，并具有良好的泛化性;
• 模型构建：定义线性回归模型类；
• 训练配置：训练相关的一些配置，如：优化算法、评价指标等；
• 组装训练框架Runner：Runner用于管理模型训练和测试过程；
• 模型训练和测试：利用Runner进行模型训练和测试。

2.5.1 数据处理

2.5.1.2 数据清洗

对数据集中的缺失值或异常值等情况进行分析和处理，保证数据可以被模型正常读取。

• 缺失值分析

import pandas as pd  # 开源数据分析和操作工具

# 利用pandas加载波士顿房价的数据集
data = pd.read_csv("boston_house_prices.csv")
# 预览前5行数据
data.head()
print(data.isna().sum())  # 查找缺失值

从输出结果看，波士顿房价预测数据集中不存在缺失值的情况。

• 异常值处理

通过箱线图直观的显示数据分布，并观测数据中的异常值。箱线图一般由五个统计值组成：最大值、上四分位、中位数、下四分位和最小值。一般来说，观测到的数据大于最大估计值或者小于最小估计值则判断为异常值

import matplotlib.pyplot as plt # 可视化工具

# 箱线图查看异常值分布
def boxplot(data, fig_name):
    # 绘制每个属性的箱线图
    data_col = list(data.columns)
    
    # 连续画几个图片
    plt.figure(figsize=(5, 5), dpi=300)
    # 子图调整
    plt.subplots_adjust(wspace=0.6)
    # 每个特征画一个箱线图
    for i, col_name in enumerate(data_col):
        plt.subplot(3, 5, i+1)
        # 画箱线图
        plt.boxplot(data[col_name], 
                    showmeans=True, 
                    meanprops={"markersize":1,"marker":"D","markeredgecolor":'#f19ec2'}, # 均值的属性
                    medianprops={"color":'#e4007f'}, # 中位数线的属性
                    whiskerprops={"color":'#e4007f', "linewidth":0.4, 'linestyle':"--"},
                    flierprops={"markersize":0.4},
                    ) 
        # 图名
        plt.title(col_name, fontdict={"size":5}, pad=2)
        # y方向刻度
        plt.yticks(fontsize=4, rotation=90)
        plt.tick_params(pad=0.5)
        # x方向刻度
        plt.xticks([])
    plt.savefig(fig_name)
    plt.show()

boxplot(data, 'ml-vis5.pdf')

结果如图:

从输出结果看，数据中存在较多的异常值（图中上下边缘以外的空心小圆圈）。

使用四分位值筛选出箱线图中分布的异常值，并将这些数据视为噪声，其将被临界值取代，代码实现如下：

# 四分位处理异常值
num_features=data.select_dtypes(exclude=['object','bool']).columns.tolist()

for feature in num_features:
    if feature =='CHAS':
        continue
    
    Q1  = data[feature].quantile(q=0.25) # 下四分位
    Q3  = data[feature].quantile(q=0.75) # 上四分位
    
    IQR = Q3-Q1 
    top = Q3+1.5*IQR # 最大估计值
    bot = Q1-1.5*IQR # 最小估计值
    values=data[feature].values
    values[values > top] = top # 临界值取代噪声
    values[values < bot] = bot # 临界值取代噪声
    data[feature] = values.astype(data[feature].dtypes)

# 再次查看箱线图，异常值已被临界值替换（数据量较多或本身异常值较少时，箱线图展示会不容易体现出来）
boxplot(data, 'ml-vis6.pdf')

 结果如图:

从输出结果看，经过异常值处理后，箱线图中异常值得到了改善。

2.5.1.3 数据集划分

import torch

torch.seed()

# 划分训练集和测试集
def train_test_split(X, y, train_percent=0.8):
    n = len(X)
    shuffled_indices = torch.randperm(n) # 返回一个数值在0到n-1、随机排列的1-D Tensor
    train_set_size = int(n*train_percent)
    train_indices = shuffled_indices[:train_set_size]
    test_indices = shuffled_indices[train_set_size:]

    X = X.values
    y = y.values

    X_train=X[train_indices]
    y_train = y[train_indices]
    
    X_test = X[test_indices]
    y_test = y[test_indices]

    return X_train, X_test, y_train, y_test 

X = data.drop(['MEDV'], axis=1)
y = data['MEDV']

X_train, X_test, y_train, y_test = train_test_split(X,y)# X_train每一行是个样本，shape[N,D]

2.5.1.4 特征工程

为了消除纲量对数据特征之间影响，在模型训练前，需要对特征数据进行归一化处理，将数据缩放到[0, 1]区间内，使得不同特征之间具有可比性。

代码实现如下：

import torch

X_train = torch.tensor(X_train,torch.float32)
X_test = torch.tensor(X_test,torch.float32)
y_train = torch.tensor(y_train,torch.float32)
y_test = torch.tensor(y_test,torch.float32)

X_min = torch.min(X_train,axis=0)
X_max = torch.max(X_train,axis=0)

X_train = (X_train-X_min)/(X_max-X_min)

X_test  = (X_test-X_min)/(X_max-X_min)

# 训练集构造
train_dataset=(X_train,y_train)
# 测试集构造
test_dataset=(X_test,y_test)

2.5.2 模型构建

import torch 

torch.seed()  # 设置随机种子
class Op(object):
    def __init__(self):
        pass

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        raise NotImplementedError

    def backward(self, inputs):
        raise NotImplementedError
# 线性算子
class Linear(Op):
    def __init__(self, input_size):

        self.input_size = input_size

        # 模型参数
        self.params = {}
        self.params['w'] = torch.randn(self.input_size, 1)
        self.params['b'] = torch.zeros([1])

    def __call__(self, X):
        return self.forward(X)

    # 前向函数
    def forward(self, X):
        N, D = X.shape

        if self.input_size == 0:
            return torch.full([N, 1], fill_value=self.params['b'])

        assert D == self.input_size  # 输入数据维度合法性验证

        # 使用torch.matmul计算两个tensor的乘积
        y_pred = torch.matmul(X, self.params['w']) + self.params['b']s
        return y_pred
input_size = 12
model=Linear(input_size)

2.5.3 完善Runner类

模型定义好后，围绕模型需要配置损失函数、优化器、评估、测试等信息，以及模型相关的一些其他信息（如模型存储路径等）。

在本章中使用的Runner类为V1版本。其中训练过程通过直接求解解析解的方式得到模型参数，没有模型优化及计算损失函数过程，模型训练结束后保存模型参数。

训练配置中定义:

• 训练环境，如GPU还是CPU，本案例不涉及；
• 优化器，本案例不涉及；
• 损失函数，本案例通过平方损失函数得到模型参数的解析解；
• 评估指标，本案例利用MSE评估模型效果。

在测试集上使用MSE对模型性能进行评估。

import torch.nn as nn
mse_loss = nn.MSELoss()

具体实现:

import torch
import os
from nndl.opitimizer import optimizer_lsm
class Runner(object):
    def __init__(self, model, optimizer, loss_fn, metric):
        # 优化器和损失函数为None,不再关注

        # 模型
        self.model = model
        # 评估指标
        self.metric = metric
        # 优化器
        self.optimizer = optimizer

    def train(self, dataset, reg_lambda, model_dir):
        X, y = dataset
        self.optimizer(self.model, X, y, reg_lambda)

        # 保存模型
        self.save_model(model_dir)

    def evaluate(self, dataset, **kwargs):
        X, y = dataset

        y_pred = self.model(X)
        result = self.metric(y_pred, y)

        return result

    def predict(self, X, **kwargs):
        return self.model(X)

    def save_model(self, model_dir):
        if not os.path.exists(model_dir):
            os.makedirs(model_dir)

        params_saved_path = os.path.join(model_dir, 'params.pdtensor')
        torch.save(model.params, params_saved_path)

    def load_model(self, model_dir):
        params_saved_path = os.path.join(model_dir, 'params.pdtensor')
        self.model.params = torch.load(params_saved_path)


optimizer = optimizer_lsm

# 实例化Runner
runner = Runner(model, optimizer=optimizer, loss_fn=None, metric=mse_loss)

2.5.4 模型训练

在组装完成Runner之后，我们将开始进行模型训练、评估和测试。首先，我们先实例化Runner，然后开始进行装配训练环境，接下来就可以开始训练了，相关代码如下：

# 模型保存文件夹
saved_dir = '深度学习'

# 启动训练
runner.train(train_dataset,reg_lambda=0,model_dir=saved_dir)

打印出训练得到的权重：

columns_list = data.columns.to_list()
weights = runner.model.params['w'].tolist()
b = runner.model.params['b'].item()
for i in range(len(weights)):
    print(columns_list[i],"weight:",weights[i])
print("b:",b)

结果如下:

2.5.5 模型测试

加载训练好的模型参数，在测试集上得到模型的MSE指标。

# 加载模型权重
runner.load_model(saved_dir)
mse = runner.evaluate(test_dataset)
print('MSE:', mse.item())

结果如下:

 2.5.6 模型预测

使用Runner中load_model函数加载保存好的模型，使用predict进行模型预测，代码实现如下：

runner.load_model(saved_dir)
pred = runner.predict(X_test[:1])
print("真实房价：",y_test[:1].item())
print("预测的房价：",pred.item())

结果如下:

问题1：使用类实现机器学习模型的基本要素有什么优点？

• 实现简单；分类时计算量非常小，速度很快，存储资源低。
• 可用于线性/非线性分类，也可以用于回归；低泛化误差；容易解释；计算复杂度较低。

问题2：算子op、优化器opitimizer放在单独的文件中，主程序在使用时调用该文件。这样做有什么优点？

避免重复定义，方便操作，使代码更加清晰易懂

问题3：线性回归通常使用平方损失函数，能否使用交叉熵损失函数？为什么？

不能，交叉熵损失函数只和分类正确的预测结果有关。而平方损失函数还和错误的分类有关，该损失函数除了让正确分类尽量变大，还会让错误分类都变得更加平均，但实际中后面的这个调整使没必要的。但是对于回归问题这样的考虑就显得重要了，因而回归问题上使用交叉熵并不适合。

总结

参考了老师给出的一些代码，了解了部分关于数据集的操作和方法

参考

https://www.cnblogs.com/hbuwyg/p/16617442.html