强化学习——Proximal Policy Optimization Algorithms
文章目录
- 前言
- 为什么需要PPO
- TRPO
- PPO
前言
本文对论文《Proximal Policy Optimization Algorithms》进行总结,如有错误,欢迎指出。
为什么需要PPO
随机策略梯度的数学表达式为
∇ J ( θ ) = E S [ E A ∼ π ( . ∣ S ; θ ) [ Q π ( S , A ) ∇ θ ln π ( A ∣ S ; θ ) ] ] (1.0) \nabla J(\theta)=E_S[E_{A\sim \pi(.|S;\theta)}[Q_\pi(S,A)\nabla_{\theta}\ln\pi(A|S;\theta)]]\tag{1.0} ∇J(θ)=ES[EA∼π(.∣S;θ)[Qπ(S,A)∇θlnπ(A∣S;θ)]](1.0)
如无特殊提及,本文中的 A A A表示动作, S S S表示状态, π \pi π表示策略。每使用一次式1.0更新策略网络,就需要策略网络控制智能体与环境交互,从而获得 S S S与 A A A,这种做法非常耗时。若能在训练前提前采样好 S S S与 A A A,并将其存储在经验回放数组中,接着从经验回放数组中抽取 S S S与 A A A训练策略网络,这将将极大程度减少训练时间。基于上述考虑,便有了Proximal Policy Optimization(PPO),在介绍PPO之前,我们先介绍下TRPO。
TRPO
TPRO利用重要性采样,对随机策略梯度进行近似,从而利用经验回放数组快速更新策略网络。依据期望的数学定义,可得重要性采样的数学形式:
E x ∼ p [ f ( x ) ] = E x ∼ q [ p ( x ) q ( x ) f ( x ) ] (2.0) E_{x \sim p}[f(x)]=E_{x \sim q}[\frac{p(x)}{q(x)}f(x)]\tag{2.0} Ex∼p[f(x)]=Ex∼q[q(x)p(x)f(x)](2.0)
值得一提的是,式2.0等式两侧的分布虽然期望形式一致,但是方差却不同:
V a r x ∼ p [ f ( x ) ] = E x ∼ p [ f ( x ) 2 ] − ( E x ∼ p [ f ( x ) ] ) 2 V a r x ∼ q [ p ( x ) q ( x ) f ( x ) ] = E x ∼ p [ f ( x ) 2 p ( x ) q ( x ) ] − ( E x ∼ p [ f ( x ) ] ) 2 \begin{aligned} Var_{x\sim p}[f(x)]&=E_{x\sim p}[f(x)^2]-(E_{x\sim p}[f(x)])^2\\ Var_{x\sim q}[\frac{p(x)}{q(x)}f(x)]&=E_{x\sim p}[f(x)^2\frac{p(x)}{q(x)}]-(E_{x\sim p}[f(x)])^2 \end{aligned} Varx∼p[f(x)]Varx∼q[q(x)p(x)f(x)]=Ex∼p[f(x)2]−(Ex∼p[f(x)])2=Ex∼p[f(x)2q(x)p(x)]−(Ex∼p[f(x)])2
当分布 p ( x ) p(x) p(x)与 q ( x ) q(x) q(x)近似时,式2.0等式两侧分布的方差也近似。
利用式2.0对式1.0进行数学变化可得
∇ J ( θ ) = E S [ E A ∼ π ( . ∣ S ; θ ) [ Q π ( S , A ) ∇ θ ln π ( A ∣ S ; θ ) ] ] = E S [ E A ∼ π ′ ( . ∣ S ; θ o l d ) [ π ( A ∣ S ; θ ) π ′ ( A ∣ S ; θ o l d ) Q π ( S , A ) ∇ θ ln π ( A ∣ S ; θ ) ] ] ≈ E S [ E A ∼ π ′ ( . ∣ S ; θ o l d ) [ π ( A ∣ S ; θ ) π ′ ( A ∣ S ; θ o l d ) Q π ′ ( S , A ) ∇ θ ln π ( A ∣ S ; θ ) ] ] (2.1) \begin{aligned} \nabla J(\theta)&=E_S[E_{A\sim \pi(.|S;\theta)}[Q_\pi(S,A)\nabla_{\theta}\ln\pi(A|S;\theta)]]\\ &=E_S[E_{A\sim \pi'(.|S;\theta_{old})}[\frac{\pi(A|S;\theta)}{\pi'(A|S;\theta_{old})}Q_\pi(S,A)\nabla_{\theta}\ln\pi(A|S;\theta)]]\\ &\approx E_S[E_{A\sim \pi'(.|S;\theta_{old})}[\frac{\pi(A|S;\theta)}{\pi'(A|S;\theta_{old})}Q_{\pi'}(S,A)\nabla_{\theta}\ln\pi(A|S;\theta)]]\tag{2.1} \end{aligned} ∇J(θ)=ES[EA∼π(.∣S;θ)[Qπ(S,A)∇θlnπ(A∣S;θ)]]=ES[EA∼π′(.∣S;θold)[π′(A∣S;θold)π(A∣S;θ)Qπ(S,A)∇θlnπ(A∣S;θ)]]≈ES[EA∼π′(.∣S;θold)[π′(A∣S;θold)π(A∣S;θ)Qπ′(S,A)∇θlnπ(A∣S;θ)]](2.1)
当策略 π \pi π与策略 π ′ \pi' π′近似时,有 Q π ( S , A ) ≈ Q π ′ ( S , A ) Q_\pi(S,A)\approx Q_{\pi'}(S,A) Qπ(S,A)≈Qπ′(S,A),由此可得式2.1中第三行的约等于符号。为了让策略 π \pi π与策略 π ′ \pi' π′近似,因此TPRO将策略 π \pi π与策略 π ′ \pi' π′的KL散度作为正则项。总体的损失函数为
max L ( θ ) = max E A ∼ π ′ ( . ∣ S ; θ o l d ) , S [ π ( A ∣ S ; θ ) π ′ ( A ∣ S ; θ o l d ) V π ( S ) ] − β K L ( π ( A ∣ S ; θ ) , π ′ ( A ∣ S ; θ o l d ) ) \begin{aligned} \max L(\theta)=\max E_{{A\sim \pi'(.|S;\theta_{old})},S}[\frac{\pi(A|S;\theta)}{\pi'(A|S;\theta_{old})}V_{\pi}(S)]-\beta KL(\pi(A|S;\theta),\pi'(A|S;\theta_{old})) \end{aligned} maxL(θ)=maxEA∼π′(.∣S;θold),S[π′(A∣S;θold)π(A∣S;θ)Vπ(S)]−βKL(π(A∣S;θ),π′(A∣S;θold))
E A ∼ π ′ ( . ∣ S ; θ o l d ) , S [ π ( A ∣ S ; θ ) π ′ ( A ∣ S ; θ o l d ) V π ( S ) ] E_{{A\sim \pi'(.|S;\theta_{old})},S}[\frac{\pi(A|S;\theta)}{\pi'(A|S;\theta_{old})}V_{\pi}(S)] EA∼π′(.∣S;θold),S[π′(A∣S;θold)π(A∣S;θ)Vπ(S)]对 θ \theta θ的求导结果即为式2.1, β \beta β为超参数。训练前,利用策略 π ′ ( A ∣ S ; θ o l d ) \pi'(A|S;\theta_{old}) π′(A∣S;θold)(可以是使用过去参数 θ o l d \theta_{old} θold的策略网络)控制智能体与环境交互,将一系列动作与状态对( s t s_t st, a t a_t at)存入经验回放数组中。训练时,从经验回放数组抽取一系列动作与状态,依据上述损失函数,利用梯度上升法更新策略网络(KL散度项如何计算可以参考交叉熵)。
PPO
PPO对TRPO的优化目标进行了改动,设 r ( θ ) = π ( A ∣ S ; θ ) π ′ ( A ∣ S ; θ o l d ) r(\theta)=\frac{\pi(A|S;\theta)}{\pi'(A|S;\theta_{old})} r(θ)=π′(A∣S;θold)π(A∣S;θ), A = V π ( S ) A=V_\pi(S) A=Vπ(S),则优化目标(省略了部分符号)变为
max L c l i p ( θ ) = max E A ∼ π ′ , S [ min ( r ( θ ) A , c l i p ( r ( θ ) , 1 − ϵ , 1 + ϵ ) ) A ) ] (3.0) \begin{aligned} \max L^{clip}(\theta)=\max E_{A\sim \pi',S}[\min (r(\theta)A,clip(r(\theta),1-\epsilon,1+\epsilon))A)]\tag{3.0} \end{aligned} maxLclip(θ)=maxEA∼π′,S[min(r(θ)A,clip(r(θ),1−ϵ,1+ϵ))A)](3.0)
c l i p ( r ( θ ) , 1 − ϵ , 1 + ϵ ) ) clip(r(\theta),1-\epsilon,1+\epsilon)) clip(r(θ),1−ϵ,1+ϵ))表示当 r ( θ ) < 1 − ϵ r(\theta)<1-\epsilon r(θ)<1−ϵ时,会被截断为 1 − ϵ 1-\epsilon 1−ϵ,当 r ( θ ) > 1 + ϵ r(\theta)>1+\epsilon r(θ)>1+ϵ时,会被截断为 1 + ϵ 1+\epsilon 1+ϵ。 ϵ \epsilon ϵ为超参数。式3.0的取值图像为
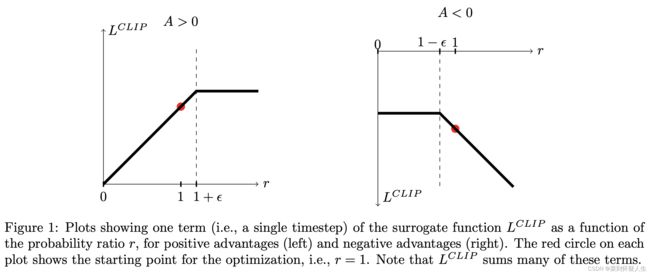
其基本思路为,当 r ( θ ) r(\theta) r(θ)位于 [ 1 − ϵ , 1 + ϵ ] [1-\epsilon,1+\epsilon] [1−ϵ,1+ϵ]时,策略 π \pi π与策略 π ′ \pi' π′较为近似,此时式2.1中的约等于符号成立,此时的梯度约等于随机策略梯度(式1.0)。当 r ( θ ) r(\theta) r(θ)不位于 [ 1 − ϵ , 1 + ϵ ] [1-\epsilon,1+\epsilon] [1−ϵ,1+ϵ]时,此时梯度与随机策略梯度差距较大,梯度提供的信号可能是错误的,因此更新参数的幅度应该要弱些。
基于上述分析,我们来看下Figure 1。当A>0时,若 r ( θ ) r(\theta) r(θ)取值大于 1 + ϵ 1+\epsilon 1+ϵ,梯度可能包含错误的信息,此时更新参数的梯度满足
0 < ( 1 − ϵ ) Q π ′ ( S , A ) ∇ θ ln π ( A ∣ S ; θ ) ( 用 于 更 新 的 梯 度 ) < π ( A ∣ S ; θ ) π ′ ( A ∣ S ; θ o l d ) Q π ′ ( S , A ) ∇ θ ln π ( A ∣ S ; θ ) 0<(1-\epsilon)Q_{\pi'}(S,A)\nabla_{\theta}\ln\pi(A|S;\theta)(用于更新的梯度)<\frac{\pi(A|S;\theta)}{\pi'(A|S;\theta_{old})}Q_{\pi'}(S,A)\nabla_{\theta}\ln\pi(A|S;\theta) 0<(1−ϵ)Qπ′(S,A)∇θlnπ(A∣S;θ)(用于更新的梯度)<π′(A∣S;θold)π(A∣S;θ)Qπ′(S,A)∇θlnπ(A∣S;θ)
即使用较小的梯度更新参数。若 r ( θ ) r(\theta) r(θ)取值小于 1 − ϵ 1-\epsilon 1−ϵ时,梯度可能包含错误的信息,此时更新参数的梯度满足
( 1 − ϵ ) Q π ′ ( S , A ) ∇ θ ln π ( A ∣ S ; θ ) > π ( A ∣ S ; θ ) π ′ ( A ∣ S ; θ o l d ) Q π ′ ( S , A ) ∇ θ ln π ( A ∣ S ; θ ) ( 用 于 更 新 的 梯 度 ) > 0 (1-\epsilon)Q_{\pi'}(S,A)\nabla_{\theta}\ln\pi(A|S;\theta)>\frac{\pi(A|S;\theta)}{\pi'(A|S;\theta_{old})}Q_{\pi'}(S,A)\nabla_{\theta}\ln\pi(A|S;\theta)(用于更新的梯度)>0 (1−ϵ)Qπ′(S,A)∇θlnπ(A∣S;θ)>π′(A∣S;θold)π(A∣S;θ)Qπ′(S,A)∇θlnπ(A∣S;θ)(用于更新的梯度)>0
即使用较小的梯度更新参数。当A<0时,若 r ( θ ) r(\theta) r(θ)取值大于 1 + ϵ 1+\epsilon 1+ϵ,梯度可能包含错误的信息,此时更新参数的梯度满足
0 > ( 1 + ϵ ) Q π ′ ( S , A ) ∇ θ ln π ( A ∣ S ; θ ) > π ( A ∣ S ; θ ) π ′ ( A ∣ S ; θ o l d ) Q π ′ ( S , A ) ∇ θ ln π ( A ∣ S ; θ ) ( 用 于 更 新 的 梯 度 ) 0>(1+\epsilon)Q_{\pi'}(S,A)\nabla_{\theta}\ln\pi(A|S;\theta)>\frac{\pi(A|S;\theta)}{\pi'(A|S;\theta_{old})}Q_{\pi'}(S,A)\nabla_{\theta}\ln\pi(A|S;\theta)(用于更新的梯度) 0>(1+ϵ)Qπ′(S,A)∇θlnπ(A∣S;θ)>π′(A∣S;θold)π(A∣S;θ)Qπ′(S,A)∇θlnπ(A∣S;θ)(用于更新的梯度)
此时发现即使梯度中包含有错误信息,PPO仍使用其更新策略网络参数。对此一个理解是既然 A < 0 A<0 A<0,表明这个动作不被提倡,因此依然使用较大的梯度更新网络,以使其尽量不做出该动作,当 r ( θ ) r(\theta) r(θ)取值小于 1 − ϵ 1-\epsilon 1−ϵ时同理。原文的解释如下
With this scheme, we only ignore the change in probability ratio when it
would make the objective improve, and we include it when it makes the objective worse
PPO在A<0部分的做法有点违反我的直觉,事实上,《Mastering Complex Control in MOBA Games with Deep Reinforcement Learning》一文指出PPO在A<0时会导致策略网络难以收敛,由此提出了Dual PPO,在A<0时,式3.0的取值为下图(b),当取值大于 c c c时,此时使用较小的梯度做更新。