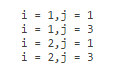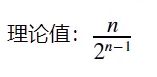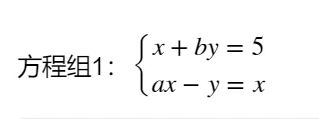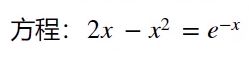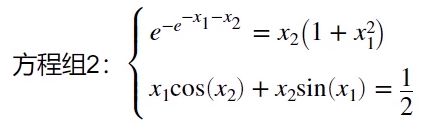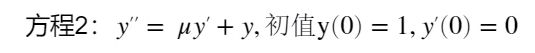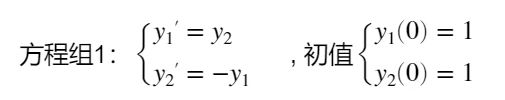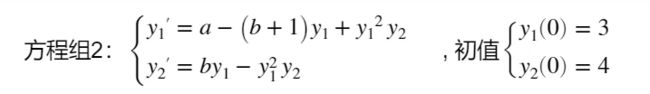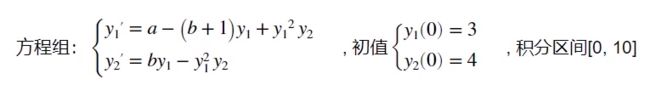Matlab基础笔记

前言

内容来自b站【数学建模 | 零基础教程】MATLAB入门+数模竞赛算法精讲+国赛赛题精讲

网页链接：https://www.bilibili.com/video/BV1YU4y1J7L5?p=15

用于记录课上的代码内容，如有错误，望指正。

Matlab简介

MATLAB = Matrix(矩阵) + Laboratory(实验室),矩阵实验室;有强大的矩阵计算和计算能力

MATLAB界面和各个窗口：

布局：默认布局和自定义布局
Ctrl + 滚轮：实施编辑器的缩放
Alt +Enter：代码和文本的切换

Ctrl + i:智能缩进

Ctrl + ]:增加缩进

Ctrl + r:快速注释代码段

Ctrl + t :快速取消注释代码段
分节符：插入分节符，代码的分块运行

简易计算

计算：[71 + (100 - 97) × 8] ÷ 64

(71 + (100-97)*8)/64^0.5;

计算：sin( π ) +cos(tan(1/5))

sin(pi^0.5)+cos(tan(1/5));

常用函数

abs(-1.2);%绝对值 复数的模
sqrt(100); %开方
mod(9,4); %取余
%exp() %指数函数
%log() %对数 底为e
%log10()
%log2()
exp(1);
log(exp(1));
log10(100);
log2(4);
%三角函数
%sin()
%cos()
%tan()
%统计相关函数
%sum()
%mean()均值
%std()标准差 方差:(std())^2
%var() 方差
%cov() 协方差
%max()
%min()
%range() 极差max() - min()
%median() 中位数
%mode() 众数

01矩阵的定义

1.1定义空矩阵

m = [];

1.2定义一个m*n的矩阵

%一行一列
m = [1];
%行矩阵（元素用空格或逗号分隔）
m2 = [1 2 3];
m3 = [4,5,6];
%列矩阵（分号表示换行）
m4 = [1;2;3];
%m行n列的矩阵
m5 = [1,2,3;4 5 6];

1.3使用冒号运算符生成矩阵

% m = 初始值：步长：终值（步长默认为1）
m6 = 1:10;
m7 = 1:0.5:10;

% m = linspace(初始值，终值，点数)(点数默认是100)
linspace(1,10,10);
linspace(1,10,100);

1.4拼凑和变形

%矩阵的拼凑
[m2,m3]; %行拼接
[m2;m3]; %列拼接
%矩阵的变形
%reshape(矩阵,要变成的形状)
reshape(m6,[2,5]); %不是顺着一行的，运行一下你就知道了

1.5几个特殊矩阵

%单位矩阵 eye(n) n为阶数
n = 3;
eye(n);

%全0矩阵 zeros(n) n为阶数
% zeros([m,n]) m为行数，n为列数
zeros(n);
zeros(3,5);
zeros([3,5]);

%全1矩阵 ones(n) n为阶数
%        ones([m,n]) m为行数，n为列数
ones(n);
ones([2,3]);

%三维矩阵 应用：黑白图像（二维矩阵）、
%彩色图像（三维矩阵，RGB三个通道，每个通道都是一个二维矩阵）
ones([5,5,3]); %[行 列 页 ]

1.6随机数矩阵

%随机数矩阵
%rand：0-1之间的数（返回的数值服从均匀分布）
%rand(n):n阶
%rand([m,n]):m为行数，n为列数
rand;
rand(n);
rand([3,5]);

%randn用法同rand(服从高斯分布（正态分布）)
randn;
randn(n);
randn([3,5]);

1.7获取矩阵的行列数

m = rand([3,5]);
sz = size(m);
[row,col] = size(m);

1.8矩阵转置、逆矩阵

m = randi(10,3);
m';%转置矩阵
inv(m);&逆矩阵

1.9特征值和特征向量

m = randi(10,3);
[V,D] = eig(m); %V：特征向量矩阵，D：特征值矩阵，对角元素为特征值

1.10加 减 乘 除 乘方 运算

a = [1,2;3,4];
b = a;
a + b;
a - b;
a*b;  %矩阵的乘法并不是元素一一相乘
a.*b; %对应元素相乘
a/b;  %等价于a*inv(b)
a*inv(b);
a^5;  %a*a*a*a*a
a.^5; %对应元素的五次方

1.11广播机制

a = [1,2;3,4];
b = 1;
a + b;%把b广播成[1,1;1,1]
a - b;

1.12逻辑运算

赋值运算符=

等号运算符==（逻辑运算符：返回0或1）

a = [1,2;3,4];
b = [2,1;3,4];
a == b; %对每个元素进行逻辑判断
a > b;
a == 1; %广播机制 判断矩阵中有没有哪个数为1
a > 1;
%保留a大于2的元素，将小于等于2的元素置为0
a.*(a > 2);

02矩阵的索引

m = [1,2,3;4,5,6;7,8,9];
m(8);             %列方向检索，第八个位置
m([1,3,5]);       %列方向检索，第1，3，5个位置的元素
m(2,3);           %第二行第三列位置的元素
m([1,2],3);       %第一二行的第三个元素
m([1,2],[1,2]);   %第一二行、第一二列的元素
m([1,2],[1,2,3]); %前两行元素
%1:3冒号运算符（初始值:步长:终值）（步长默认为1）
%linspace         详情见01的1.3
m(1:2,1:3);       %后两行元素
m(1:3,2:3);       %后两列的元素

03变量类型和转化

1.1数值类型

%double类型
%数值和数值矩阵
%可进行 加 减 乘 除 逻辑 运算
a = 1;
b = [1,2];

1.2字符串类型

%string类型：用单引号或双引号括起来
%字符串和字符串矩阵
%可进行加法运算（字符串的拼接）
s1 = "hello";
s2 = "world";
[s1,s2];
s1 + " " +s2;

1.3字符串和数值的转化

%str2num():字符串转数字
str2num("5") + 4;
%num2str():数值换字符串，第二个参数为有效数字的位数
num2str(1/3,2);

1.4输入语句

value = input('请输入一个值：');%输入数组或矩阵
string = input('请输入名字','s');%要输入字符串，需要加第二个参数's'
%视频里用的是""(双引号)，但是我的软件报错，所以我用单引号

1.5输出语句

value = 5;
disp(value);
disp('樂y');            %可以用双引号    disp("樂y")
disp(["hello","world"]) %跟视频不一样的是，输出是列排序
disp(["hello",2])       %跟视频不一样的是，输出是列排序
%如果hello用单引号括起来，2是没有被更改为string类型，也不会输出
disp(["1/3 = " + num2str(1/3,2)])
%输出1/3 = 0.33(2有效数字为两位) 有效数字是指从左边第一个非零数起

04运算符和if...else控制语句

1.1关系运算符

>

>=

<

<=

==

非零值都是True，0是false

1.2逻辑运算符

% 与 &(当两边条件都为true时，返回1，否则返回0)
% 或 |(当两边条件有一个为true时，就返回1，条件都为false，返回0)
% 非 ~(取反)
(1 < 2) & (1 > 2);
(1 < 2) | (1 > 2);
~((1 < 2) | (1 > 2));
(1 < 2) & ~(1 > 2);

1.3if...else控制语句

%if 条件1
%   语句1
%elseif 条件2
%   语句2
%else
%   语句3
%end
value = input('请输入一个数:');
if(value == 1)
    disp("1既不是质数也不是合数")
elseif(isprime(value))
    disp("输入是质数")
else
    disp("输入是合数")
end

05For循环和While循环

1.1for循环

%for index = value
%    语句
%end
for i = [1,3,5]
    disp(i)
end

%求1 + 2 + 3 + ... + 100
sum = 0;
for i = [1:100]
    sum = sum + i;
end

%二重for循环
for i =1:3 %执行3次
    for j = 1:5 %执行5次
        disp([i,j])
    end
end

1.2while循环

%while 表达式（为真）
%   语句
%end
n = 1;
while n < 5
    disp(n)
    n = n + 1;
end
%for循环和while循环都可以嵌套，也可以互相嵌套

06控制退出循环的关键字Break、Continue和Return

1.1for循环没有关键字代码

for i = 1:2
    for j = 1:3
        disp(["i = " + num2str(i) + ",j = " + num2str(j)]);
    end
end

1.2Contine关键字

for i = 1:2
    for j = 1:3
        if(j == 2)
            continue;%结束当前循环（continue后面的语句不再执行）
        end
        disp(["i = " + num2str(i) + ",j = " + num2str(j)]);
    end
end

1.3Return关键字

for i = 1:2
    for j = 1:3
        if(j == 2)
            return;%退出多层循环
        end
        disp(["i = " + num2str(i) + ",j = " + num2str(j)]);
    end
end

1.4Break关键字

for i = 1:2
    for j = 1:3
        if(j == 2)
            break;%退出整层循环（一层）
        end
        disp(["i = " + num2str(i) + ",j = " + num2str(j)]);
    end
end

07练习题

1.生成[min,max]之间的随机（整数）数矩阵

min和max为用户输入，行列数为用户输入

小数或整数由用户指定，最后输出结果（如何使每次输出结果相同？）

相关知识点：input、if...else、rand、randi、disp

val = input('请输入数组范围[min,max]:');
size = input('请输入数组行列数[row,coml]:');
cho = input('请输入矩阵类型 0）小数 1）整数');
if(cho == 0)     %小数矩阵
   res = (val(2) - val(1))*rand(size) + val(1) 
elseif(cho == 1) %整数矩阵
    res = randi(val,size);
else
    disp('输入数字有误');
end
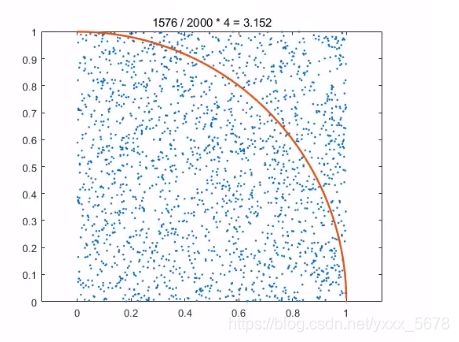
disp(res);

2.模拟圆周率pi

参考思路:蒙特卡罗法;点数为用户输入值

相关知识点: input、if...else、for循环或while循环、rand、disp

allPoints = input('请输入生成的总点数：');
count = 0;
for i = 1:allPoints
    if rand^2 + rand ^2 <= 1 
        %圆的方程x^2 + y^2 <=1才在圆内
        %rand生成的是(0,1)范围的
        count = count + 1;
    end
end
res = count / allPoints * 4 %除4是因为1/4个圆

3.斐波那契数列的第n项和前n项和

n为用户输入值1,1,2,3,5,8,13,21,34,55......
递推公式:F[n] = F[n-1]+F[n-2];
相关知识点: input、for循环或while循环、disp

N = input('请指定数列的项数：');
res = [1,1];    %将斐波那契数列前两项进行存储
for i =3:N
    element =  res(length(res)) + res(length(res) - 1)
    %注意1不是在res里面进行减的
    res = [res,element];
    %将res跟element的元素进行拼接
end
disp(res);
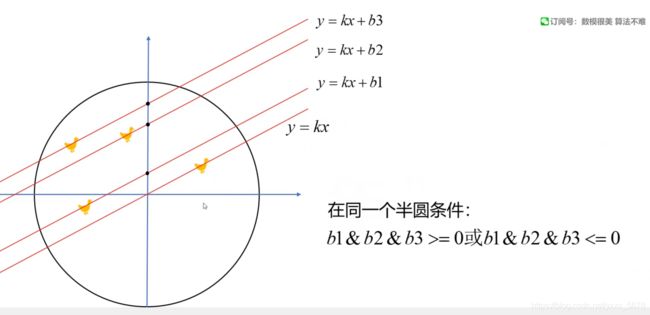
disp(sum(res));

4.圆中四只鸭子在同一个半圆的概率

参考思路:蒙特卡罗法（进行N次试验，每次试验生成4个随机点，统计四点在同一个半圆的个数)
关知识点: input、if...else、for循环或while循环、rand、disp

 

 4.1简单代码：存在冗余

N = 4;      %四只鸭子
total = 100000; %实验总数
count = 0;
for e = 1:total
    p1 = 2*[rand,rand] - 1;%rand[0,1] 把范围弄成[-1,1]
    p2 = 2*[rand,rand] - 1;
    p3 = 2*[rand,rand] - 1;
    p4 = 2*[rand,rand] - 1;
    
    %将p1作为第一点计算斜率，其余点计算截距
    k = p1(2) / p1(1); %k = y /x
    b1 = p2(2) - k*p2(1); %y = kx +b → b = y - kx
    b2 = p3(2) - k*p3(1); 
    b3 = p4(2) - k*p4(1); 
    if(b1 >= 0 &b2 >= 0 & b3 >=0) | (b1 <= 0 & b2 <= 0 & b3 <= 0)
        count = count + 1;
        continue;
        %如果在p1作为斜率满足截距的式子，下面的就不用走了
    end
    
    %将p2作为第一点计算斜率，其余点计算截距
    k = p2(2) / p2(1); %k = y /x
    b1 = p1(2) - k*p1(1); %y = kx +b → b = y - kx
    b2 = p3(2) - k*p3(1); 
    b3 = p4(2) - k*p4(1); 
    if(b1 >= 0 &b2 >= 0 & b3 >=0) | (b1 <= 0 & b2 <= 0 & b3 <= 0)
        count = count + 1;
        continue;
        %如果在p2作为斜率满足截距的式子，下面的就不用走了
    end
    
    k = p3(2) / p3(1); 
    b1 = p1(2) - k*p1(1); 
    b2 = p2(2) - k*p2(1); 
    b3 = p4(2) - k*p4(1); 
    if(b1 >= 0 &b2 >= 0 & b3 >=0) | (b1 <= 0 & b2 <= 0 & b3 <= 0)
        count = count + 1;
        continue; 
    end
    
    k = p3(2) / p3(1); 
    b1 = p1(2) - k*p1(1); 
    b2 = p2(2) - k*p2(1); 
    b3 = p4(2) - k*p4(1); 
    if(b1 >= 0 &b2 >= 0 & b3 >=0) | (b1 <= 0 & b2 <= 0 & b3 <= 0)
        count = count + 1;
        continue; 
    end
    
    k = p3(2) / p3(1); 
    b1 = p1(2) - k*p1(1); 
    b2 = p2(2) - k*p2(1); 
    b3 = p4(2) - k*p4(1); 
    if(b1 >= 0 &b2 >= 0 & b3 >=0) | (b1 <= 0 & b2 <= 0 & b3 <= 0)
        count = count + 1;
        continue; 
    end
end
res = count / total;
disp(res);

 4.2优化代码

N = 4;      %四只鸭子
total = 100000; %实验总数
count = 0;
for e = 1:total
    p1 = 2*[rand,rand] - 1;%rand[0,1] 把范围弄成[-1,1]
    p2 = 2*[rand,rand] - 1;
    p3 = 2*[rand,rand] - 1;
    p4 = 2*[rand,rand] - 1;
    p = [p1;p2;p3;p4]; %构造一个四行两列的数组
  
    for i = 1:N
        k = p(i,2) / p(i,1);
        b = [];%初始化b，为一个空数组，方便添加东西进里面
        for j = 1:N
            if j == i
                continue;
                %用我的这个作为斜率，那我不需要计算我当前的截距
            else
                b = [b,p(j,2) - k*p(j,1)];
                %将截距存入b
            end
        end
        if(b(1) >= 0 &b(2) >= 0 & b(3) >=0) | (b(1) <= 0 & b(2) <= 0 & b(3) <= 0)
            %记住将b后面的数字用()括起来
             count = count + 1;
             break;
             %已经判断在这个斜率下，b满足条件的，这个点就不用继续在其他斜率下判断了
             %跳出的是第二个for循环(i的那个for循环)
        end
    end

end
res = count / total;
disp(res);

08函数、匿名函数和脚本

1.1函数

%function[输出参数]= myfun(输入参数)
%   函数体;
%end
s = area(2);
s = area([1,2]); %调用时都要写到function的前面
[s,count] = areaAndLen(1,1);
%圆的面积
function s = area(r);
    s = pi * r.^2;
end

%圆的周长
function c = len(r);
    c = 2*pi*r;
end

%圆的面积和周长
function [s,c] = areaAndLen(r,pi) %视频里用PI
%但其实是有误的，还是有严格区分字母大小写的
    s = pi *r.^2;
    c = 2 * pi * r;
end

1.2匿名函数

%f = @(输入参数) 函数体
%f :函数句柄
f = @(x)x.^2;
f(2);
f([2,3]); %x可以是个数组，将数组里的数带入函数体
f1 = @(x,y)x.^2 + y.^2 + 2*x.*y; %(x+y)^2
f1(2,3);
f1([1,2,3],6); %广播机制f([1,2,3],[6,6,6])
%[1,2,3]各个作为x，6作为y

1.2.1匿名函数和函数的转化

f2 = @fun;
f2(5);
f3 = @(x)fun(x);
f3(6);
function y = fun(x)
    y = x.^2;
end

1.2.2使用场景

%函数体复杂时，使用函数
%函数体简单时，使用匿名函数
f4 = @fun;
f4 = (-3);
f5 = @(x)fun(x);
f5(-6);
function y = fun(x)
    if x >= 0
        y = x;
    else
        y = -x;
    end
end

a = 5;
f4 = @fun;
f4 = (-3,a);%这里调用就要写a
f5 = @(x)fun(x,a);%前面括号不用加a
f5(-6);%这里调用就不用写a
function y = fun(x,a)
    if x >= a
        y = x;
    else
        y = -x;
    end
end

 1.3脚本

实际上就是后缀m的文件;

当文件里只有函数时，就成为函数脚本文件或函数文件;

函数文件可被其他脚本调用（需要在同一文件目录下)，也可在命令行调用。

%area.m的文件下
function s = area(r)
    s = pi * r.^2;
end
%Script.mlx文件下
area(2)

%GetMatrix.m文件下
function s = GetMatrix(isInt,val,sz)
    if(isInt == 0)     %小数矩阵
        s = (val(2) - val(1))*rand(sz) + val(1) 
        %注意接收的是s,跟函数接受的值一样
    elseif(isInt == 1) %整数矩阵
        s = randi(val,sz);
    else
        disp('输入数字有误');
    end
end
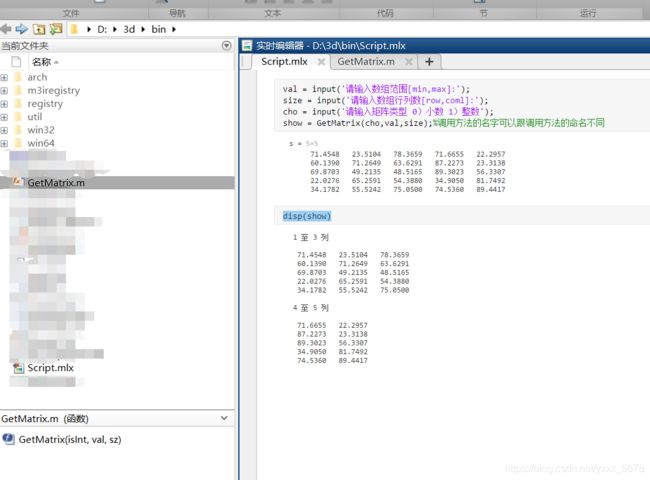
%Script.mlx文件下
val = input('请输入数组范围[min,max]:');
size = input('请输入数组行列数[row,coml]:');
cho = input('请输入矩阵类型 0）小数 1）整数');
show = GetMatrix(cho,val,size);%调用方法的名字可以跟调用方法的命名不同
disp(show)

 1.3.1练习题

圆中N只鸭子在同一个半圆的概率

参考思路:蒙特卡罗法(进行M次试验，每次试验生成N个随机点，统计N点在同一个半圆的个数)

要求使用函数脚本文件。

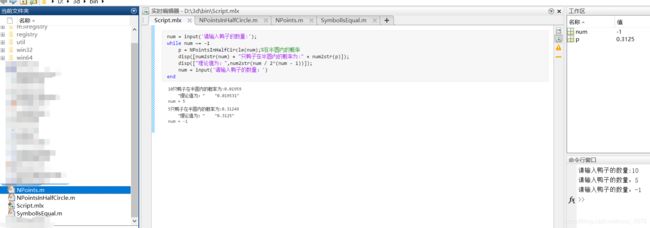
%在Script.mlx文件下
num = input('请输入鸭子的数量:');
while num ~= -1
    p = NPointsInHalfCircle(num);%在半圆内的概率
    disp([num2str(num) + "只鸭子在半圆内的概率为:" + num2str(p)]);
    disp(["理论值为：",num2str(num / 2^(num - 1))]);
    num = input('请输入鸭子的数量：')
end

%在NPointsInHalfCircle.m文件下
function p = NPointsInHalfCircle(num)
    N = num;      %num只鸭子
    total = 100000; %实验总数
    count = 0;
    for e = 1:total
        %生成N个随机点
        p = NPoints(N);
        %依此让每个点作为第一个点，计算斜率
        for i = 1:N
            k = p(i,2) / p(i,1);
            b = [];%初始化b，为一个空数组，方便添加东西进里面
            %计算截距
            for j = 1:N
                if j == i
                    continue;
                %用我的这个作为斜率，那我不需要计算我当前的截距
                else
                    b = [b,p(j,2) - k*p(j,1)];
                %将截距存入b
                end
            end
        %判断N-1个截距的符号一致性
            if SymbolIsEqual(b)
                count = count + 1;
                break;
            end
        end
    
    end
    p = count / total;

end

%在NPoints.m文件下
function p = NPoints(N)
    p = [];
    for i = 1:N
        p = [p;2*[rand,rand]-1]; %[N,2]
        %范围在[-1,1]
    end
end

%在SymbolIsEqual.m文件下
function isEqual = SymbolIsEqual(b)
    isEqual = 1;
    %首先判断b的首元素的正负号，根据首元素正负号分两种情况，判断后面元素的正负号
    if b(1) >= 0
        for i = 2:length(b)
            if b(i) < 0
                isEqual = 0;
                break;
            end
        end
    else %b(1) <  0
        for i = 2:length(b)
            if b(i)>=0
                isEqual = 0;
                break;
            end
        end
    end
end

 09Matlab绘图与图形界面GUI

基本思想：连点成线

1.1二维绘图命令plot

绘制y = sin (x)

x = linspace(0,2*pi,100);
y = sin(x);
plot(x,y);

1.2一幅图形绘制多条曲线

%方式一：hold
%hold on    开启图像保持功能，绘制多个图形对象
%hold off   关闭图形保持功能
x = linspace(0,2*pi,100);
y = sin(x);
y2 = cos(x);
plot(x,y);
hold on;
plot(x,y2);
hold off;
%方式二：plot(x1,y1,x2,y2,……)
plot(x,y,x,y2);

1.3添加坐标轴标签（label）、标题（title）、图例（legend）

x = linspace(0,2*pi,100);
y = sin(x);
y2 = cos(x);
plot(x,y,x,y2);
xlabel('x');
ylabel('y = sin(x) , y2 = cos(x)');
title('y =  sin(x) , y2 = cos(x)');
legend('y = sin(x) , y2 = cos(x)');

1.4绘制多幅图figure

x = linspace(0,2*pi,100);
y = sin(x);
y2 = cos(x);
figure;plot(x,y);
figure;plot(x,y2);

1.5绘制多个子图subplot

%subplot(m,n,i):m行n列 第i个图形
x = linspace(0,2*pi,100);
y = sin(x);
y2 = cos(x);
y3 = x.^2;
y4 = x.^0.5;
subplot(2,2,1);plot(x,y); %两行两列的第一个
subplot(2,2,2);plot(x,y2);%两行两列的第二个
subplot(2,2,3);plot(x,y3);%两行两列的第三个
subplot(2,2,4);plot(x,y4);%两行两列的第四个

1.6绘图修饰

线型、线宽、颜色、描点类型、网格、坐标轴刻度……

%plot(x,y,'- r o') 线性、颜色、描点类型（顺序可变）
%线型：-实线、--虚线、:电线、-.点画线
%描点类型：.点、o圆、x叉号、+加号、*星号
%           <、>、^、v（三角形）
%           s方形、d菱形、p五角星、h六角星
%颜色：      r红色、g绿色、b蓝色、y黄色、w白色、k黑色
x = linspace(0,2*pi,30);
y = sin(x);
plot(x,y,'- r x');
plot(x,y,'- b p',...
    'LineWidth',1,...           %线宽
    'MarkerEdgeColor','r',...   %描点边框颜色
    'MarkerFaceColor','y',...   %描点内部填充颜色
    'MarkerSize',10)            %描点大小

% grid on添加网格
% grid off取消网格
%axis on 显示坐标轴、刻度线和坐标轴标签
%axis off关闭坐标轴、刻度线、坐标轴标签
%axis([xmin,xmax,ymin,ymax]) 设置x轴和y轴的显示范围
%axis equal 沿每个坐标轴使用相同的数据单位长度
%axis square 使用相同长度的坐标轴线。相应调整数据单位之间的增量
x = linspace(0,2*pi,100);
y = sin(x);
y2 = cos(x);
y3 = x.^2;
y4 = x.^0.5;
subplot(2,2,1);plot(x,y);grid on;
subplot(2,2,2);plot(x,y2);axis off;
subplot(2,2,3);plot(x,y3);axis ([-10,10,0,100]);
subplot(2,2,4);plot(x,y4);axis equal;

1.7绘制GIF动图

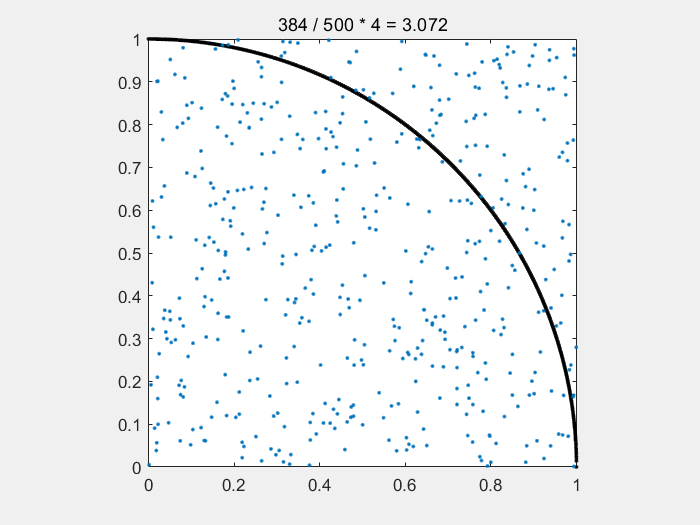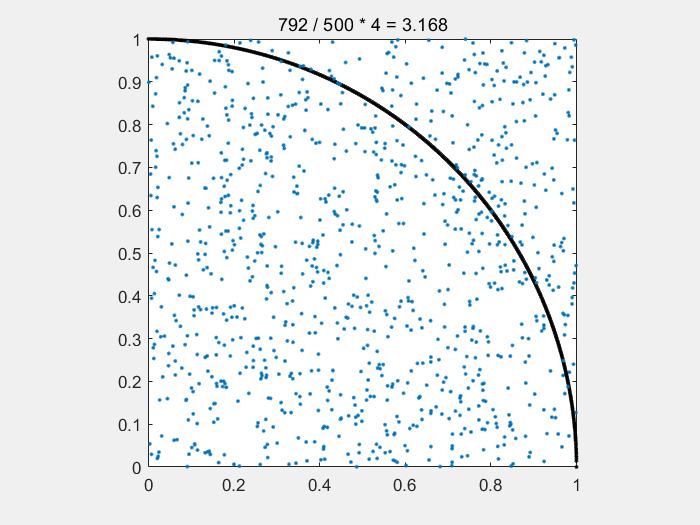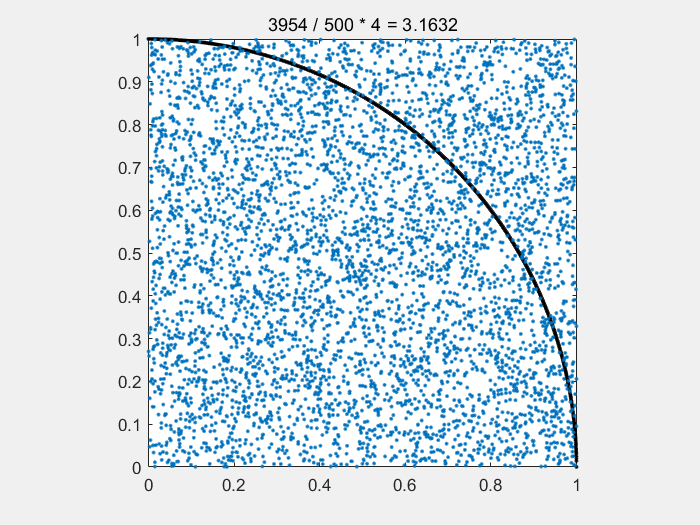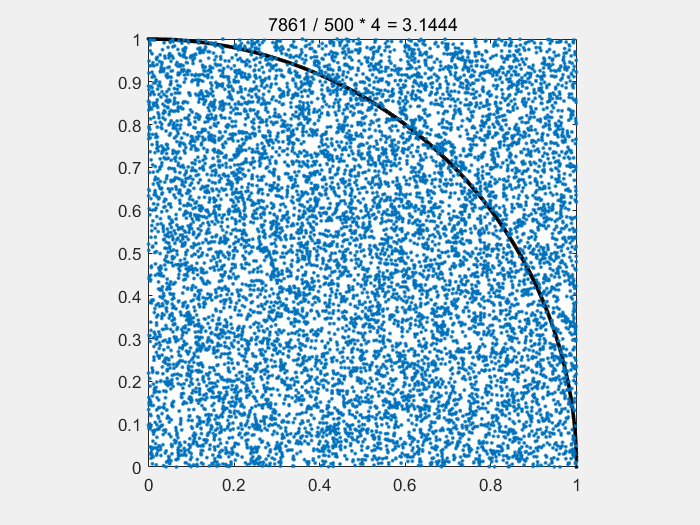
基本思想:先生成多张静态图，然后组合成 gif图

for i = [500,1000,2000,5000,10000]
    x1 = linspace(0,1,10000);
    y1 = (1-x1.^2).^0.5;
    x2 = rand([1,i]);
    y2 = rand([1,i]);
    count = 0;
    for j = 1:i
        if x2(j)^2 + y2(j)^2 <=1
            count = count + 1;
        end
    end
    plot(x1,y1,'k.',x2,y2,".");
    title([num2str(count) + " / " + num2str(500) + " * " + "4" + " = " + num2str(count/i*4)]);
%在1/4圆里面，所以除4
    axis square;  

    frame = getframe(gcf);%捕获坐标区或图窗作为影片帧
    I = frame2im(frame);%返回与影片帧关联的图像数据
    [I,map] = rgb2ind(I,256);%将RGB图像转换为索引图像I，关联颜色图为map
    if i == 500
        imwrite(I,map,'test.gif','gif','Loopcount',inf,'DelayTime',0.2);
    else
        imwrite(I,map,'test.gif','gif','WriteMode','append','DelayTime',0.2);
    end
end

1.8更多二维绘图命令

1.8.1errorbar 含误差条的线图

%errorba：含误差条的线图
%errorbar(x,y,err) 绘制y对x的图，并在每个数据点处绘制一个垂直误差条
x = linspace(0,100,10);
y = x.^0.5;
err = rand(size(x));
errorbar(x,y,err,'both');%both对x、y轴都显示了误差

1.8.2histogram 直方图

%histogram:直方图
%histogram(x,n) 基于x创建直方图，n为区间数量
x = randn([1,10000]);
n = 10;
histogram(x,n);%10000个点在[-5,5]的分布

1.8.3scatter 散点图

%scatter(x,y) 在向量 x 和 y 指定的位置创建一个包含圆形的散点图
%用法类似plot
x = linspace(0,2*pi,30);
y = sin(x);
scatter(x,y,'o','MarkerEdgeColor','b','MarkerFaceColor','r');

1.8.4bar 柱状图

%bar(y) 创建一个条形图，y中的每个元素对应一个条形
%如果y是m×n矩阵，则bar创建每组包含n个条形的m个组
y = [2 3 6;11 23 26];
bar(y);

1.8.5pie 饼图

%pie(x,explode) 使用X中的数据绘制饼图，饼图的每个扇区代表x中的每一个元素
%explode 将扇区从饼区偏移一定位置
x = [1 3 0.5 2.5 2];
explode = [0 1 0 1 0];%每个数对应每个数所占比值偏移的位置量
pie(x,explode);

1.9三维绘图之曲线、曲面和散点图

1.9.1三维曲线plot3

% plot3(X1,Y1,Z1,LineSpec1,.. . ,Xn , Yn,Zn,LineSpecn)
% %用法类似plot
X = linspace(0,6*pi,200);
y = sin(x);
z = cos(x);
xlabel('x');
ylabel('sin(x)');
zlabel('cos(x)');
title('y = sin(X) , z = cos(X)');
plot3(y,z,x);

1.9.2散点图scatter3

%scatter3 用法类似scatter
x = linspace(0,6*pi,300);
y = sin(x);
z = cos(x);
scatter3(x,y,z,'o','MarkerEdgeColor','b',"MarkerFaceColor",'r');

1.9.3三维曲面mesh、surf

基本思想:连点成面

%meshgrid：网格

%[x,y]=meshgrid(a,b);meshgrid函数生成x乘y的矩阵

%X：通过将a复制length(b)-1行得到

%Y：首先对b进行转置得到b'，将b'复制（length(a)-1）次得到
x = 1:3;
y = 1:5;
[x,y] = meshgrid(x,y);

%mesh 网格图
%surf 曲面图
%绘制z = x * e^(-(x^2 + y^2))
[x,y] = meshgrid(-10:1:10);%跟meshgrid(-10:1:10,-10:1:10)一样的
z = x.*exp(-x.^2 - y.^2);
mesh(x,y,z);
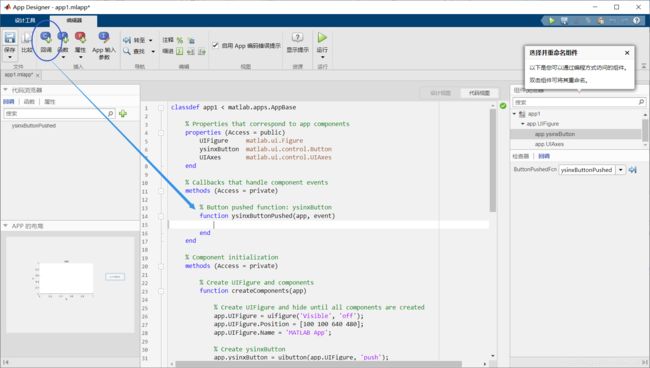
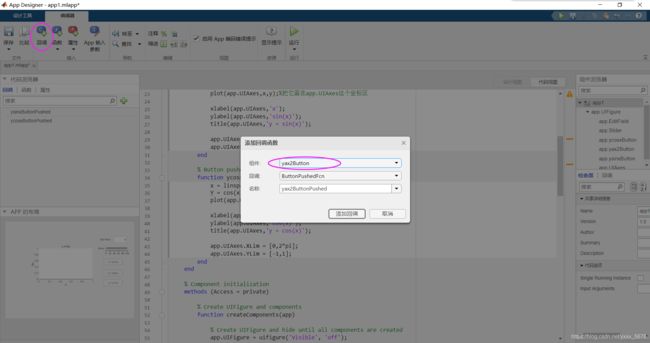
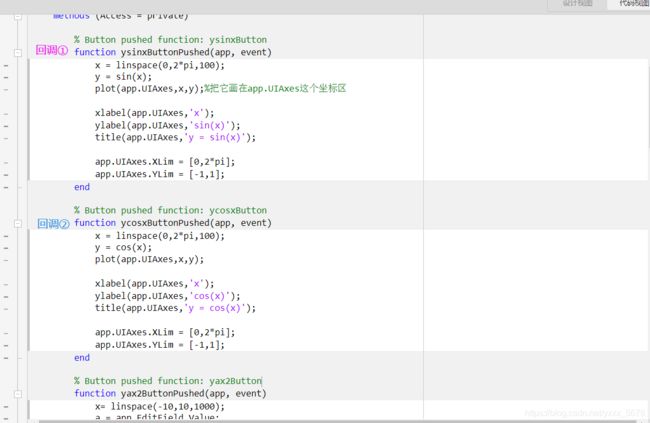
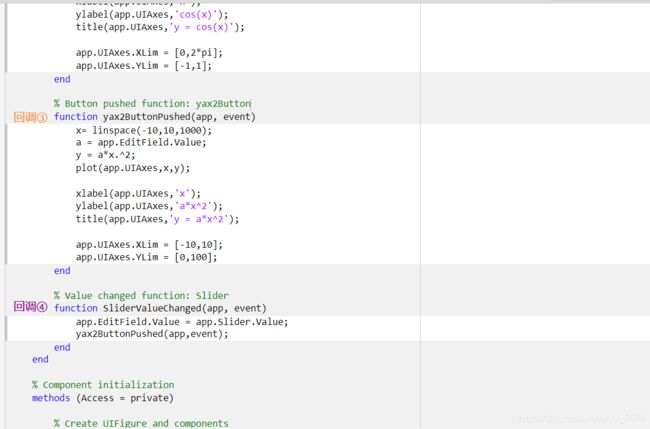
surf(x,y,z)

1.10图形用户界面

(Graphical User Interface，简称GUI)

 

 

 

 

 

 

 

 其余的代码，代码试图已写好。

10文件读写

将数据写入文件: writetable (txt、Excel)

从文件读取数据: readtable (txt、Excel)

1.1将数据写入文件

基本步骤:首先构造 table，然后将table写入文件

% writetable(m,filename):将m写入名为filename的文件
% %支持的文件扩展名: .txt、.csv、.xls、.xlsm或 .xlsx
m = rand(4) +1;%返回一个 4×4 的随机数矩阵
% %rand输出（0，1）范围的数，广播机制，将随机生成的数加1
%"decimals"：小数点后的位数
%"significant"：有效数字的位数
%m = round(m,2,"decimals");
m = round(m,2,"significant");
t = table(m)
writetable(t,'m.txt');%相对地址
writetable(t,'D:\3d\bin\m.txt');%绝对路径
%delimiter（指定分隔符）：“，”（默认）、“ ”、“\t”、“；”、“|”
writetable(t,'m.txt',"Delimiter","\t");%\t将数据进行水平对齐
type m.txt;

%"WriteVariableNames":是否写入变量名
writetable(t,'m.txt',"Delimiter","\t","WriteVariableNames",false);
type m.txt;

%将多个矩阵保存在同一个文件
t2 = table(eye(4));%4*4单位矩阵
writetable(t2,'m.txt',"Delimiter","\t","WriteVariableNames",false," WriteMode","append");%追加进m.txt
type m.txt;

1.2从文件读取数据

% t = readtable(filename)从filename文件中读取数据
%支持的扩展名: .txt、.cs;v、.xls、.xlsb、.xlsm、.xlsx、.xltm、.xltx
%t = readtable( "m.txt");
t = readtable( "D:\3d\bin\m.txt")
m = table2array(t)

 

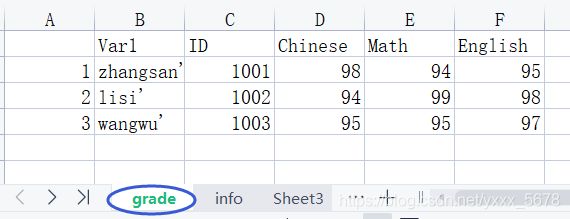
 两表如图所示，以下代码利用上表

t_grade = readtable("Student.xls","Sheet","grade");
t_info = readtable("Student.xls","Sheet","info");
t_grade = readtable("Student.xls","Sheet",1);%第一个表；其实就是grade表
t_info = readtable("Student.xls","Sheet",2);%第二个表；其实就是grade表
readtable("Student.xls","Sheet",3);%因为第三个表没有，所以显示空
sheetnames("student.xls");%输出excel里面表的名称
length(sheets);%输出excel里面有多少个表
table2array(t_grade);%表中有两种类型 一个是double 一个是cell
%数组有个要求就是类型要一样，所以这句话会报错

1.3table更多用法

%table的构造
Names = {'zhangsan';'lisi';'wangwu'};
ID = {1001;1002;1003};
Chinese = {98;94;95};
Math = {94;99;95};
English = {95;98;97};
t_grade = table(Names,ID,Chinese,Math,English);
table(ID,Chinese,Math,English,'RowNames',Names);%将names空
%访问表格元素
%1.通过索引（和矩阵一致）
t_grade(1,2);
t_grade(1,1:5);
t_grade(1,:);%跟上面的结果是一样的
t_grade(:,[1,3]);%所有行都输出，指定列为1跟3
%2.通过列名获取
t_grade(:,"ID");
t_grade(:,{'Names','Chinese'});
%修改列名
t_grade.Properties.VariableNames(1) = {'Name'};%把第一行的Names改为Name
%增加行
%t_grade(4,:) = {'zhao',1004,95,98,100};%有些编译器可以实现
%报错：无法从double转换为cell
%增加列 报错:cell类型的操作数不支持运算符+
%t_grade.total = t_grade.Chinese + t_grade.Math + t_grade.English;
%合并表格
t_grade1 = readtable("Student.xls","Sheet","grade");
t_info = readtable("Student.xls","Sheet","info");
t_student = join(t_grade1,t_info);%将两表合并，相同内容会进行舍弃
t_student.Properties.VariableNames(1) = {'Number'};
writetable(t_student,'Student.xls',"Sheet",'student');%将上表写入Student.xls

11图像

1.1图片的读写和显示

%彩色图像：200*200*3，RGB三通道，每个通道值的范围0：255
pic = imread("pic.jpg");%读取图片
%200*200:像素点的个数，对应矩阵大小
%矩阵元素值的范围:0:255  0:黑色 255:白色
%uint8：unsigned int 8：无符号整型
imshow(pic);%显示图片
temp = pic(60:100,60:100);%截取pic图片的一部分
imshow(temp);
%随机生成一个图像
m = randi([0,255],[400,400]);
m = uint8(m);%将double类型转为uint8
imshow(m);
%创建一个渐变（0-255）图像并保存
bw = zeros([256,400]);
for i = 1:256
    for j = 1:400
        bw(i,j) = i - 1;%因为像素最多是255 所以要减一
    end
end
bw = uint8(bw);
imshow(bw);
%格式：jpg，png，jpeg，tif，bmp，ico
imwrite(bw,"bw.jpg");%将bw图片保存到当前路径下

1.2彩色图、灰度图和二值化

1.2.1RGB分离与合并

pepper = imread("flower.jpg");
imshow(pepper);

R = pepper(:,:,1);
G = pepper(:,:,2);
B = pepper(:,:,3);

subplot(2,2,1);%分块输出四个图像
imshow(pepper);
title("original");

subplot(2,2,2);
imshow(R);
title("R");

subplot(2,2,3);
imshow(G);
title("G");

subplot(2,2,4);
imshow(B);
title("B");

1.2.2彩色图转灰度图 rgb2gray

%彩色图转灰度图 rgb2gray()
%原理：通过计算R G B分量的加权和，将RGB值转换为灰度值
pepper = imread("flower.jpg");
pepper_gray = rgb2gray(pepper);%里面不能直接传照片 要用imread转换为数组
imshow(pepper_gray);

1.2.3二值化 imbinarize

%方法一：自己写
pepper = imread("flower.jpg");
pepper_gray = rgb2gray(pepper);%里面不能直接传照片 要用imread转换为数组
[row,col] = size(pepper_gray);
for i = 1:row
    for j = 1:col
        if pepper_gray(i,j) > 128
            pepper_gray(i,j) = 1;
        else
            pepper_gray(i,j) = 0;
        end
    end
end
pepper_bw = logical(pepper_gray);
imshow(pepper_bw);

%方法二：编译自带函数

%method - 用于二值化图像的方法：'global'（默认） | 'adaptive'
%'Sensitivity' - 自适应阈值的敏感度银子：0.50（默认） | [0,1]范围内的数值
%'ForegroundPolarity' - 确定哪些像素被视为前景像素：'bright'（默认) | 'dark'
%'bright':前景比背景亮
%'dark'：前景比背景暗
pepper_gray1 = rgb2gray(pepper);
bw = imbinarize(pepper_gray1,'adaptive','ForegroundPolarity',"bright","Sensitivity",0.4);
imshow(bw);

作用：有一些照片，文字部分存在一部分暗，一部分亮，可用此方法来区分背景与文字内容。

1.3MATLAB中图像处理相关函数

1.3.1调整图像大小imresize

%I = imresize(pic,scale);scale为缩放倍数
%I = imresize(pic,[row,col]);调整大小为row * col
I = imread("flower.jpg");
imshow(I);

J = imresize(I,0.5);%将图片缩小一半
imshow(J);

K = imresize(I,[200,200]);
imshow(K);

1.3.2旋转图像imrotate

%I = imrotate(pic,angle);angle为旋转的角度
I = imread("flower.jpg");
J = imrotate(I,30);%逆时针旋转了30°
imshow(J);

1.3.3图像的加减乘除

%imadd() 两幅图像相加时，要求大小一致
%imsubtract()
%immultiply() 矩阵的点乘
%imdivide() 矩阵的点除
I = imread("flower.jpg");
J = imadd(I,30);
imshow(J);
%也能实现两图片相加，前提：数组的容量相同row、col都一样
J1 = imread("flower.jpg");
K = imadd(J,J1);
imshow(K);

L = imsubtract(J,J1);
imshow(L);

M = immultiply(J,J1);
imshow(M);

1.3.4直方图图imhist和直方图均衡化histeq

I = imread("flower.jpg");
imshow(I);
imhist(I);%直方图是实现RGB数值的分布图
J = histeq(I);
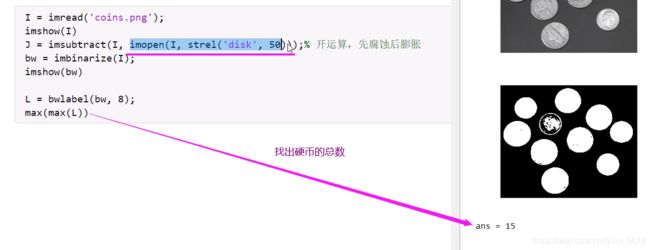
imshow(J);

1.3.5标注连通分量bwlabel

BW = logical([1 1 1 0 0 0 0 0 ;...
              1 1 1 0 1 1 0 0 ;...
              1 1 1 0 1 1 0 0 ;...
              1 1 1 0 0 0 1 0 ;...
              1 1 1 0 0 0 1 0 ;...
              1 1 1 0 0 0 1 0 ;...
              1 1 1 0 0 1 1 0 ;...
              1 1 1 0 0 0 0 0]);
imshow(BW);
L = bwlabel(BW,4);%四联通
max(max(L));
%找硬币的个数

12方程

12.1方程和方程组的解析解(solve)

solve函数用法：solve(方程1，方程2……，变量1，变量2……)

多项式合并：（x + 3x - 5x）x/4

syms x;
a = (x+3*x-5*x)*x/4;
%解得a = -x^2/4

syms a b c x;
y = a*x^2 + b*x + c;
solve(y,x)%x这个还能换成a b c 进而求出a b c

 

syms x;
y = 2*x - x^2 - exp(-x);
solve(y,x)

 

syms a b x y;
y1 = x + b*y - 5;
y2  = a*x-y-x;
res = solve(y1,y2,x,y);
res.x
res.y

 

syms x1 x2;
y1 = exp(-exp(-x1-x2)) - x2*(1+x1^2);
y2  = x1*cos(x2)+x2*sin(x1)-1/2;
res = solve(y1,y2,x1,x2);
res.x1
res.x2

1.2方程和方程组的数值解（fsolve）

fsolve函数用法：fsolve(函数句柄，初值)

初值一般是通过经验给出

f = @(x)2*x-x^2-exp(-x);%函数句柄 匿名函数
fsolve(f,0)%x赋初值为0

 

a = 3;
b = 5;%给a b赋初值
f = @(x)funs(x,a,b);
fsolve(f,[0,0])%x,y赋初值0

function y = funs(x,a,b)%x = [x,y]
    y(1) = x(1) + b*x(2) - 5;%x(1):x x(2):y
    y(2) = a*x(1) - x(2) - x(1);
end

f = @fun;
fsolve(f,[0,0])

function y = fun(x)% x = [x1,x2]
y(1) = exp(-exp(-x(1)-x(2))) - x(2)*(1+x(1)^2);
y(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 1/2;
end

1.3常微分方程和常微分方程组的解析解(dsolve)

dsolve函数用法：dsolve（方程1，方程2，……，初值1，初值2……）

syms y(x)
dsolve(diff(y) == 2*x,y(0) == 1)%diff(y)是y的一阶常微分方程

 

syms y(x) mu
eqn = diff(y,2) == mu*diff(y) + y;
cond1 = y(0) ==1;
Dy = diff(y);
cond2 = Dy(0) == 0;
dsolve(eqn,cond1,cond2)

 

syms y1(x) y2(x)
eqn1 = diff(y1) == y2;
eqn2 = diff(y2) == -y1;
cond1 = y1(0) == 1;
cond2 = y2(0) == 1;
res = dsolve(eqn1,eqn2,cond1,cond2);
res.y1
res.y2

syms y1(x) y2(x) a b
eqn1 = diff(y1) == a-(b+1)*y1+y1^2*y2;
eqn2 = diff(y2) == b*y1 - y1^2*y2;
dsolve(eqn1,eqn2);%这个方程式过于复杂，找不到解析式

 1.4常微分方程和常微分方程组的数组解

有许多常微分方程，从理论上讲解存在，但无法求出其解析解，此时，需要寻求数值解。

基本思想：

 也因此，数值解法必须提供初值。

常微分方程(组)求解solver = ode45, ode23, ode113, ode15s, ode23s

        ode45：4-5阶Runge-Kutta法

        ode23：2-3阶Runge-Kutta法

        ode113: Adams-Bashforth-Moutlon PECE算法

        ode15s:后向差分

        ode23s:修正的二阶Rosenbrock公式

函数用法: ode45(函数句柄，积分区间，初值)

​​​​​​​

%匿名函数必须同时接受两个输入（x，y），即使其中一个输入未使用也是如此
%虽然函数里面没有y 注意这里必须写两个输入
f = @(x,y)2*x;
tspan = [0,10];
y0 = 10;
[x,y] = ode45(f,tspan,y0);
plot(x,y)

%匿名函数必须同时接受两个输入（x，y），即使其中一个输入未使用也是如此
%虽然函数里面没有y 注意这里必须写两个输入
mu = 1;
f = @(x,y)fun(y,mu);
tspan = [0,20];%写成[0 20]也可以
y0 = [1 0];
[x,y] = ode45(f,tspan,y0);
plot(x,y(:,1),"r",x,y(:,2),"g")%y1'用红线画，y2'用绿线画

function ydot = fun(y,mu)
    ydot = [y(2);mu*(1-y(1)^2)*y(2)+y(1)];
end

 

a = 100;
b = 50;
f = @(x,y)fun(y,a,b);
tspan = [0,10];
y0 = [3 4];
[x,y] = ode45(f,tspan,y0);
plot(x,y(:,1),"r",x,y(:,2),"g")%y1'用红线画，y2'用绿线画

function ydot = fun(y,a,b)
    ydot = [a - (b + 1)*y(1)+y(1)^2*y(2);b*y(1) - y(1)^2*y(2)];
end