矩阵论公式总结
在线latex公式编辑
https://private.codecogs.com/latex/eqneditor.php?lang=zh-cn
矩阵云算网
http://www.yunsuan.info/matrixcomputations/index.html
文章目录
- 一、 λ \lambda λ 矩阵与 Jordan 标准形
-
- 1.1 零多项式、零次多项式
- 1.2 不变因子、行列式因子、初等因子
- 1.3 相抵
- 1.4 相似
- 1.5 初等因子与Jordan标准形的关系
-
- Jordan标准形例题
- 1.6 Cayley-Hamilton 定理
- 四、矩阵的因子分解
-
- 4.1 初等矩阵
-
- 4.1.1 初等矩阵
- 4.1.2 初等下三角矩阵
- 4.2 满秩分解
- 4.3 三角分解(LU分解)
- 4.4 QR分解
- 4.5 Schur定理与正规矩阵
- 4.6 奇异值分解
- 五、Hermite矩阵与正定矩阵
-
- 5.1 Hermite矩阵概念引入
- 5.2 Hermite矩阵二次型、正定(非负定)矩阵
- 5.3 矩阵不等式
- 六、范数与极限
-
- 6.1 向量范数
- 6.2 矩阵范数
- 6.3 矩阵序列与矩阵级数
- 七、矩阵函数
- 八、广义逆矩阵
一、 λ \lambda λ 矩阵与 Jordan 标准形
1.1 零多项式、零次多项式
零多项式: 0(没有次数)
零次多项式: 常数(次数为0,也就是 λ \lambda λ次数为0)
1.2 不变因子、行列式因子、初等因子
(1)不变因子 d ( λ ) d(\lambda) d(λ)
初等变换后得到的 d 1 ( λ ) d_{1}(\lambda) d1(λ), d 1 ( λ ) d_{1}(\lambda) d1(λ)都是首项系数为1的多项式,并且 d 1 ( λ ) ∣ d 2 ( λ ) d_{1}(\lambda)|d_{2}(\lambda) d1(λ)∣d2(λ), d 2 ( λ ) d_{2}(\lambda) d2(λ)整除 A 2 ( λ ) A_{2}(\lambda) A2(λ)的全部元素. d 1 ( λ ) d_{1}(\lambda) d1(λ), d 1 ( λ ) d_{1}(\lambda) d1(λ)…称为不变因子.

(2)行列式因子 D ( λ ) D(\lambda) D(λ)
A ( λ ) A(\lambda) A(λ)全部 k k k阶子式的最大公因式称为 A ( λ ) A(\lambda) A(λ)的 k k k阶行列式因子,记为 D k ( λ ) D_{k}(\lambda) Dk(λ).(K阶子式是指行列式)
① 先看1阶子式,假设现在是3阶矩阵,然后看9个多项式行列式的最大公因式.
② 2阶子式共9个2阶行列式,先算每个的2阶的行列式,然后综合9个求最大公因式(假如是m*n的矩阵,则共有 C m 2 ∗ C n 2 C_{m}^{2}\ast C_{n}^{2} Cm2∗Cn2 个 ).
③ 3阶子式就是直接算这个矩阵的行列式.
(3)初等因子
在得到不变因子后,除去 1 之后的因子 称为矩阵的初等因子.
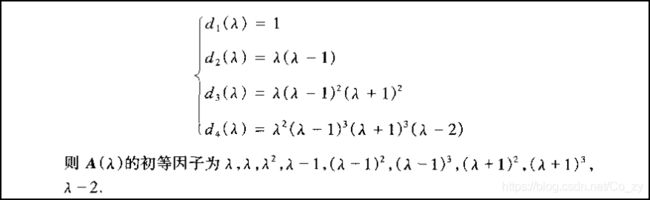
行列式因子和不变因子的关系

根据初等因子得不变因子
秩和初等因子可以唯一确定不变因子.

先从第一个开始 λ \lambda λ看,看后面有没有次数比它高的因式,有是 λ 2 \lambda^{2} λ2,往后看是 λ − 1 \lambda-1 λ−1,后面有次数更高的因式 ( λ − 1 ) 3 (\lambda-1)^{3} (λ−1)3,于是它们相乘得到 d 4 ( λ ) d_{4}(\lambda) d4(λ) ,按此方法直到最后一个.
1.3 相抵
定理3.3.1 相抵的 λ \lambda λ矩阵具有相同的秩、相同的各阶行列式因子、不变因子.
定理3.3.3 A ( λ ) A(\lambda) A(λ)和 B ( λ ) B(\lambda) B(λ)相抵<=>它们有相同的行列式因子,或者相同的不变因子.
1.4 相似
-
定理3.4.1 n阶矩阵A与B相似
<=>λ I − B \lambda I-B λI−B 和 λ I − A \lambda I-A λI−A相抵(等价). -
定义3.4.1 设A是n阶数字矩阵,其特征矩阵 λ I − A \lambda I-A λI−A 的行列式因子、不变因子、初等因子分别称为 A 的行列式因子、不变因子、初等因子.
-
定理3.4.2 n阶矩阵A与B相似
<=>它们有相同的行列式因子或者相同的不变因子或者初等因子.(两个矩阵都不可相似对角化时用这个判断,下面便是这种情况)

-
定理3.5.3 A与一个对角矩阵相似
<=>A的初等因子都是一次的.
1.5 初等因子与Jordan标准形的关系

假如现在得到的初等因子为 λ − 1 \lambda-1 λ−1, ( λ − 1 ) 2 (\lambda-1)^{2} (λ−1)2,则Jordan标准型如下:
[ 1 0 0 0 1 1 0 0 1 ] \begin{bmatrix} 1 &0 &0 \\ 0 &1 &1 \\ 0 &0 &1 \end{bmatrix} ⎣⎡100010011⎦⎤
①首先 λ − 1 \lambda-1 λ−1是一次,Jordan块是一行一列, λ \lambda λ减去的是1所以值为1,
②然后 ( λ − 1 ) 2 (\lambda-1)^{2} (λ−1)2是二次,Jordan块是两行两列,对角线值为1,因为是 ( λ − 1 ) (\lambda-1) (λ−1),对角线上面斜线内填入非零常数.
例题
求矩阵的Jordan标准形的两种方法
https://wenku.baidu.com/view/d9700a18482fb4daa58d4b60.html
Jordan标准形例题
(1) 求矩阵的Jordan标准形
方法一:

上面例子得到,对任意的n阶矩阵 A A A ,存在 n n n 阶可逆矩阵P使得 P − 1 A P = J P^{-1}AP=J P−1AP=J 为Jordan标准形.
方法二:
还有方法就是求出特征值,就得到了Jordan标准形.
代码计算Jordan标准形、变换矩阵P
import numpy as np
from sympy import Matrix
import sympy
import pprint
# 设置输出结果不用科学计数法表示
np.set_printoptions(suppress=True)
# A为要分解的矩阵
A = np.array([[1,-5,0],[0,2,0],[-2,-19,1]])
a = Matrix(A)
P, Ja = a.jordan_form()
pprint.pprint(Ja)
pprint.pprint(P)
# 这里可以输入自己计算出来的p进行验算
p = np.array([[5/9,0,-1/2],[-1/9,0,0],[1,1,1]])
p_ = np.linalg.inv(p)
J = np.dot(np.dot(p_,A),p)
pprint.pprint(J)
(2) 求变换矩阵P的方法



(3) 求完变换矩阵P后,可以用来求解 e A , e A t , s i n A t e^{A} ,e^{At} ,sinAt eA,eAt,sinAt.后面有例题.
1.6 Cayley-Hamilton 定理
定理3.6.1 设A是n阶矩阵, f ( λ ) f(\lambda) f(λ)是A的特征多项式,则 f ( A ) = 0 f(A)=0 f(A)=0.
定义3.6.1 设A为n阶矩阵, 如果存在多项式 φ ( λ ) \varphi(\lambda) φ(λ) 使得 φ ( A ) = 0 \varphi(A)=0 φ(A)=0 则称 φ ( λ ) \varphi(\lambda) φ(λ)为A的化零多项式.
对任意n阶矩阵A, f ( λ ) f(\lambda) f(λ)是A的特征多项式,由定理3.6.1知 f ( λ ) f(\lambda) f(λ)为A的化零多项式,如果 g ( λ ) g(\lambda) g(λ)是任意多项式,则 g ( λ ) g(\lambda) g(λ) f ( λ ) f(\lambda) f(λ)也是A的化零多项式(共有无穷多个).
定理3.6.2 n阶矩阵A的所有化零多项式中,次数最低且首项系数为1的多项式称为A的最小多项式.
例题 : 矩阵最小多项式的特征多项式求法 (最小多项式要去一个个试)
https://wenku.baidu.com/view/291b2e8d5fbfc77da369b145.html
四、矩阵的因子分解
4.1 初等矩阵
4.1.1 初等矩阵
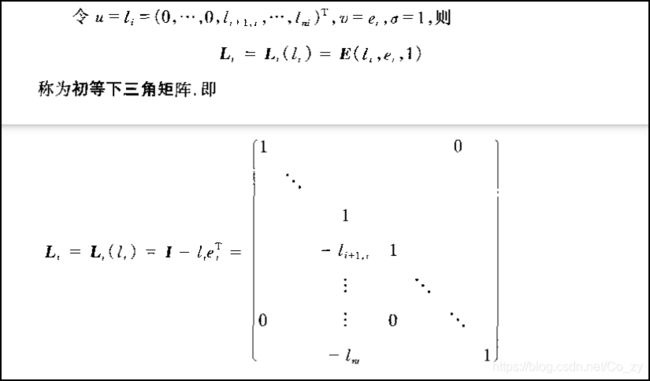
设 u , v ϵ C n u,v\epsilon \mathbb{C}^{n} u,vϵCn, σ \sigma σ为一复数,如下形式的矩阵
E ( u , v , σ ) = I − σ u v H E(u,v,\sigma)=I-\sigma uv^{H} E(u,v,σ)=I−σuvH
称为初等矩阵.
线性代数中所用的初等矩阵都可以用初等矩阵 E ( u , v , σ ) E(u,v,\sigma) E(u,v,σ) 表示,也就是用这个式子,通过给 u , v , σ u,v,\sigma u,v,σ 赋不同的值,可以倒出其他形式的矩阵,例如初等下三角矩阵、Householder矩阵(Hermite初等矩阵).
4.1.2 初等下三角矩阵
4.2 满秩分解
定理 4.2.1 满秩分解定理 设 m × n m\times n m×n 矩阵的秩为 r > 0 r>0 r>0, 则存在 m × r m\times r m×r 矩阵B和 r × n r\times n r×n 矩阵C使得 A = B C A=BC A=BC, 并且 r a n k ( B ) = r a n k ( C ) = r rank(B)=rank(C) = r rank(B)=rank(C)=r.
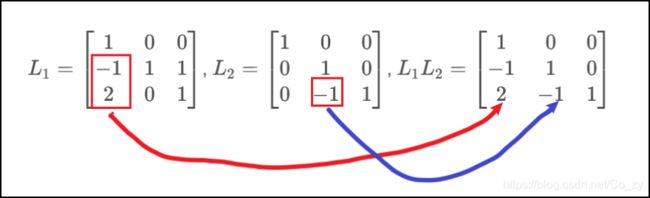
知识点1
如果
L 1 = [ 1 0 0 − 1 1 0 2 0 1 ] L_{1}=\begin{bmatrix} 1 &0 &0 \\ -1 &1 &0 \\ 2 &0 &1 \end{bmatrix} L1=⎣⎡1−12010001⎦⎤ L 2 = [ 1 0 0 0 1 0 0 − 1 1 ] L_{2}=\begin{bmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &-1 &1 \end{bmatrix} L2=⎣⎡10001−1001⎦⎤
则:
L 1 L 2 = [ 1 0 0 − 1 1 0 2 − 1 1 ] L_{1}L_{2}=\begin{bmatrix} 1 &0 &0 \\ -1 &1 &0 \\ 2 &-1 &1 \end{bmatrix} L1L2=⎣⎡1−1201−1001⎦⎤
知识点2
用初等下三角矩阵左乘一个矩阵,等于高斯消元操作
A = [ 1 2 − 1 2 − 3 4 − 2 1 2 ] → [ 1 2 − 1 0 − 7 6 0 5 0 ] A=\begin{bmatrix} 1 &2 &-1 \\ 2 &-3 &4 \\ -2 &1 &2 \end{bmatrix} \rightarrow \begin{bmatrix} 1 &2 &-1 \\ 0 &-7 &6 \\ 0 &5 &0 \end{bmatrix} A=⎣⎡12−22−31−142⎦⎤→⎣⎡1002−75−160⎦⎤
等价于
[ 1 0 0 − 2 1 0 2 0 1 ] ⋅ A = [ 1 2 − 1 0 − 7 6 0 5 0 ] \begin{bmatrix} 1 &0 &0 \\ -2 &1 &0 \\ 2 &0 &1 \end{bmatrix}\cdot A=\begin{bmatrix} 1 &2 &-1 \\ 0 &-7 &6 \\ 0 &5 &0 \end{bmatrix} ⎣⎡1−22010001⎦⎤⋅A=⎣⎡1002−75−160⎦⎤
⇒ [ 1 0 0 − 2 1 0 2 0 1 ] ⋅ [ 1 2 − 1 2 − 3 4 − 2 1 2 ] = [ 1 2 − 1 0 − 7 6 0 5 0 ] \Rightarrow \begin{bmatrix} 1 &0 &0 \\ -2 &1 &0 \\ 2 &0 &1 \end{bmatrix}\cdot \begin{bmatrix} 1 &2 &-1 \\ 2 &-3 &4 \\ -2 &1 &2 \end{bmatrix}=\begin{bmatrix} 1 &2 &-1 \\ 0 &-7 &6 \\ 0 &5 &0 \end{bmatrix} ⇒⎣⎡1−22010001⎦⎤⋅⎣⎡12−22−31−142⎦⎤=⎣⎡1002−75−160⎦⎤
A左侧的矩阵左下角的值,求法如下:

下面看一个满秩分解的例题:

4.3 三角分解(LU分解)
定理4.3.1 LU分解定理 设 A A A 是n阶非奇异矩阵,则存在唯一的单位下三角矩阵 L L L 和上三角矩阵 U U U 使得 A = L U A=LU A=LU 的充分必要条件是 A A A 的所有顺序主子式均非零.


用待定系数法,先写出LU的格式,然后一点点算.或者看下面的:

定理4.3.2 LDU分解定理 设 A A A 是 n n n阶非奇异矩阵,则存在惟一的单位下三角矩阵 L L L,对角矩阵 D = d i a g ( d 1 , d 2 , . . . , d n ) D=diag(d_{1},d_{2},...,d_{n}) D=diag(d1,d2,...,dn) 和单位上三角矩阵 U U U 使得 A = L D U A=LDU A=LDU.
接上面的例题,对U再次分解
U = [ 2 0 0 0 3 0 0 0 6 ] [ 1 1 / 2 3 / 2 0 1 1 / 3 0 0 1 ] U=\begin{bmatrix} 2 &0 &0 \\ 0 &3 &0 \\ 0 &0 &6 \end{bmatrix}\begin{bmatrix} 1 &1/2 &3/2 \\ 0 &1 &1/3 \\ 0 &0 &1 \end{bmatrix} U=⎣⎡200030006⎦⎤⎣⎡1001/2103/21/31⎦⎤
LDU分解参考 https://zhidao.baidu.com/question/988941708785428419.html
LU分解在求解线性方程组中的应用:
4.4 QR分解
定理4.4.1 设A是n阶非奇异(复)矩阵,则存在正交矩阵Q(也称酉矩阵)和非奇异实(复)上三角矩阵R使得 A = Q R A = QR A=QR, 且除去相差一个对角元绝对值(模)全等于1的对角矩阵因子外分解式(4.4.1)是惟一的.
下面先看一个例题:
例题 https://wenku.baidu.com/view/6872ac728e9951e79b892700.html

施密特正交化:

另外参考:
计算方法(三)矩阵分解1-正交分解(QR分解)
https://blog.csdn.net/weixin_33802505/article/details/91741893
4.5 Schur定理与正规矩阵
定义2.7.1 如果n阶实矩阵A满足 A T A = A A T = I A^{T}A=AA^{T}=I ATA=AAT=I则称A为正交矩阵.如果n阶复矩阵A满足 A H A = A A H = I A^{H}A=AA^{H}=I AHA=AAH=I则称A为酉矩阵.
定义4.5.1 设A,B ϵ R n × n \epsilon R ^ { n \times n} ϵRn×n ,如果存在n阶正交(酉)矩阵U使得
U T A U = U − 1 A U = B U^{T}AU=U^{-1}AU=B UTAU=U−1AU=B则称A正交(酉)相似与B.
定理4.5.1(考试不考分解计算) 任何一个 n n n阶复矩阵 A A A 都酉相似于一个上三角矩阵,即存在一个 n n n阶酉矩阵 U U U 和一个n阶上三角矩阵 R R R 使得
U H A U = R U^{H}AU = R UHAU=R其中 R R R 的对角元是 A A A 的特征值,它们可以按要求的次序排列.
定义4.5.2 设 A ϵ C m × n A\epsilon \mathbb{C}^{m\times n} AϵCm×n,如果
A A H = A H A AA^{H}=A^{H}A AAH=AHA则称A为正规矩阵.
4.6 奇异值分解
参考李航P283例题
手写求解注意:
假如 A A A 为4x2的矩阵, 分解后 U Σ V T U\Sigma V^{T} UΣVT, 分别为4x4,4x2,2x2
A A T AA^{T} AAT或者 A H A A^{H}A AHA 是去求 V T V^{T} VT,此时 V T V^{T} VT是2x2,所以 A A T AA^{T} AAT或者 A H A A^{H}A AHA需要是2x2
通过判断应该计算 A H A A^{H}A AHA,2x2
得到的特征向量需要单位化, 因为 U U U 和 V T V^{T} VT 都是正交矩阵.
下面是最早记录的内容,可能有误!
① A A H AA^{H} AAH 还是 , 这取决于A的形状,如果是 2 × 3 2 \times 3 2×3 的则用 A A H AA^{H} AAH,这样得到 2 × 2 2 \times 2 2×2,如果是后者 3 × 2 3 \times 2 3×2的,则用 A H A A^{H}A AHA.
② 求矩阵U时,先用非零特征值求 1 σ i A v i \frac{1}{\sigma_{i} }Av_{i} σi1Avi,之后再用 A T x = 0 A^{T}x=0 ATx=0 求解另一组标准正交基.
矩阵云算网
http://www.yunsuan.info/matrixcomputations/index.html
五、Hermite矩阵与正定矩阵
5.1 Hermite矩阵概念引入
定理5.1.1 A = a j k ϵ C m × n A=a_{jk} \epsilon C^{m\times n} A=ajkϵCm×n, A是Hermite矩阵的充分必要条件是对任意 x ϵ C n x\epsilon C^{n} xϵCn, x H A x x^{H}Ax xHAx是实数.
相合的定义 对两个n阶实矩阵 A A A和 B B B,若存在一个可逆实方阵 P P P,使得 B = P T A P B=P^{T}AP B=PTAP,则称 B B B和 A A A为实相合的。
矩阵的惯性 π ( A ) , v ( A ) , δ ( A ) \pi(A),v(A),\delta (A) π(A),v(A),δ(A) 分别为矩阵A的正特征值、负特征值、虚特征值的个数,记 l n ( A ) = π ( A ) , v ( A ) , δ ( A ) ln(A)={\pi(A),v(A),\delta (A)} ln(A)=π(A),v(A),δ(A)则称 l n ( A ) ln(A) ln(A) 为矩阵A的惯性.
定理5.1.6 Sylvester惯性定律 设A,B均为n阶Hermite矩阵,则A与B相合的充分必要条件是 l n ( A ) = l n ( B ) ln(A)=ln(B) ln(A)=ln(B)
紧跟着上一条如下,简单点说: 实对称矩阵的秩 等于 非零特征值的个数.
5.2 Hermite矩阵二次型、正定(非负定)矩阵
先看一下实数中的二次型
https://wenku.baidu.com/view/c993a930783e0912a3162a0b.html


( s = Π ( A ) s= \Pi(A) s=Π(A) 代表的是正特征值的个数,看上面这里r-s就好理解了,因为实对称矩阵的秩 等于 非零特征值的个数).
正定的充分必要条件

以下内容在证明中用的较多:

证明过程:

接上一张


定理5.2.3 n阶Hermite矩阵A正定的充分必要条件是A的顺序主子式均为正数
定理5.2.3 n阶Hermite矩阵A正定的充分必要条件是A的所有主子式全大于零.
例题5.2.2

注解1: 若 A C = C A AC=CA AC=CA 这个条件去掉,则AC特征值大于0
注解2: 若 A > 0 , C ⩾ 0 A>0,C\geqslant 0 A>0,C⩾0且 A C = C A AC=CA AC=CA,则 A C ⩾ 0 AC\geqslant0 AC⩾0
定理5.2.6 n阶Hermite矩阵A正定的充分必要条件是存在n阶非奇异下三角矩阵L使得 A = L L H A=LL^{H} A=LLH这个式子称为正定矩阵A的Cholesky分解.
注解: 若 A > 0 , A H = A A>0,A^{H}=A A>0,AH=A , 则A的对角元 a i j > 0 a_{ij}>0 aij>0.
另外可参考 Cholesky分解及一个例子
定义5.2.2 设 A , B ∈ C m × n A,B\in C ^{ m \times n} A,B∈Cm×n,如果存在负数 λ \lambda λ 和非零向量 x ∈ C n x \in C^{n} x∈Cn使得 A x = λ B x ( 5.2.5 ) Ax=\lambda Bx \qquad (5.2.5) Ax=λBx(5.2.5)则称 λ \lambda λ为广义特征值问题 A x = λ B x Ax=\lambda Bx Ax=λBx 的特征值,非零向量 x x x 称为对应于特征值 λ \lambda λ的特征向量.
★定理5.2.7 设A,B均为n阶Hermite矩阵,且 B > 0 B>0 B>0,则存在非奇异矩阵P使得 P H A P = d i a g ( λ 1 , . . . , λ n ) , P H B P = I P^{H}AP=diag(\lambda_{1},...,\lambda_{n}), P^{H}BP=I PHAP=diag(λ1,...,λn),PHBP=I其中 λ 1 , . . . , λ n \lambda_{1},...,\lambda_{n} λ1,...,λn是广义特征值问题(上面5.2.5)的特征值.
(注意:这里A,B是实对称矩阵, B > 0 B>0 B>0,对于A不知道.)

5.3 矩阵不等式
定义5.3.1 设A,B都是n阶Hermite矩阵,如果 A − B ≥ 0 A-B\geq0 A−B≥0,则称A大于或等于B,记作 A ≥ B A\geq B A≥B.
定理5.3.1 设A,B,C均为n阶Hermite矩阵,则 A ≥ B ( A B > B ) A\geq B(AB>B) A≥B(AB>B)的充分必要条件是对任意n阶可逆矩阵P都有
⑴ P H A P ≥ P H B P ( P H A P > P H B P ) P^{H}AP\geq P^{H}BP(P^{H}AP> P^{H}BP) PHAP≥PHBP(PHAP>PHBP)
⑵ 若 A > 0 ( A ≥ 0 ) , C > 0 ( C ≥ 0 ) A>0(A\geq 0),C>0(C\geq 0) A>0(A≥0),C>0(C≥0),且 A C = C A AC=CA AC=CA,则 A C > 0 ( A C ≥ 0 ) AC>0(AC\geq 0) AC>0(AC≥0)
定理5.3.3 设A是n阶Hermite矩阵,则 λ m i n ( A ) I ≤ A ≤ λ m a x ( A ) I \lambda _{min}(A)I\leq A \leq \lambda_{max}(A)I λmin(A)I≤A≤λmax(A)I, 这时 λ m a x ( A ) \lambda _{max}(A) λmax(A)和 λ m i n ( A ) \lambda _{min}(A) λmin(A)分别表示A的最大和最小特征值.
定理5.3.4 设A,B均为n阶Hermite正定矩阵,则
(1)若 A ≥ B > 0 A\geq B>0 A≥B>0,则 B − 1 ≥ A − 1 > 0 B^{-1} \geq A^{-1}>0 B−1≥A−1>0.
(2)若 A > B > 0 A> B>0 A>B>0,则 B − 1 > A − 1 > 0 B^{-1} > A^{-1}>0 B−1>A−1>0.

定理5.3.5 设A.B均为n阶Hermite正定矩阵,且AB=BA,则
(1)若 A ≥ B A\geq B A≥B,则 A 2 ≥ B 2 A^{2}\geq B^{2} A2≥B2.
(2)若 A > B A>B A>B,则 A 2 > B 2 A^{2} > B^{2} A2>B2.

六、范数与极限
6.1 向量范数
1范数: 各个元素的绝对值之和
∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ \parallel x\parallel _{1}=\sum_{i=1}^{n}\mid x_{i}\mid ∥x∥1=i=1∑n∣xi∣
2范数: 每个元素的平方和再开平方根
∥ x ∥ 2 = ( ∑ i = 1 n ∣ x i ∣ 2 ) 1 2 \parallel x\parallel _{2}=(\sum_{i=1}^{n}\mid x_{i}\mid^{2})^{\frac{1}{2}} ∥x∥2=(i=1∑n∣xi∣2)21
∞ \infty ∞范数
∥ x ∥ ∞ = m a x 1 ≤ i ≤ n ∣ x i ∣ \parallel x\parallel _{\infty}=\mathop{max}\limits_{1\leq i \leq n} \mid x_{i} \mid ∥x∥∞=1≤i≤nmax∣xi∣
p范数
∥ x ∥ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 p , 1 ≤ p < + ∞ \parallel x\parallel _{p}=(\sum_{i=1}^{n}\mid x_{i}\mid^{p})^{\frac{1}{p}},1\leq p<+\infty ∥x∥p=(i=1∑n∣xi∣p)p1,1≤p<+∞

6.2 矩阵范数
定义 6.2.2 相容范数

定理6.2.3
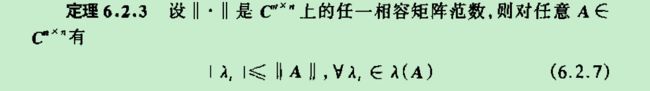

★ 其中 ρ ( A ) = m a x 1 ≤ i ≤ n ∣ λ i ∣ \rho(A)=\mathop{max} \limits_{1 \leq i \leq n}\mid \lambda_{i} \mid ρ(A)=1≤i≤nmax∣λi∣
矩阵的1-范数 (列和范数)(列模)
矩阵的每一列上的元素绝对值先求和,再从中取个最大的(列和最大)
∥ A ∥ 1 = m a x 1 ≤ j ≤ n ∑ i = 1 m ∣ a i j ∣ \parallel A\parallel _{1}=\mathop{max}\limits_{1\leq j \leq n} \sum_{i=1}^{m}\mid a_{ij} \mid ∥A∥1=1≤j≤nmaxi=1∑m∣aij∣
矩阵的2-范数 (谱范数)(谱模)
矩阵 A.T*A 的最大特征值开平方根
∥ A ∥ 2 = ( λ m a x ( A H A ) ) 1 2 \parallel A\parallel _{2}=(\lambda_{max}(A^{H}A))^{\frac{1}{2}} ∥A∥2=(λmax(AHA))21
矩阵的无穷范数 (行和范数)(行模)
矩阵的每一行上的元素绝对值先求和,再从中取个最大的(行和最大)
∥ A ∥ ∞ = m a x 1 ≤ i ≤ m ∑ j = 1 n ∣ a i j ∣ \parallel A\parallel _{\infty}=\mathop{max}\limits_{1\leq i \leq m} \sum_{j=1}^{n}\mid a_{ij} \mid ∥A∥∞=1≤i≤mmaxj=1∑n∣aij∣
矩阵的F范数
各元素绝对值和再开根号
∥ A ∥ F = t r ( A H A ) = ( ∑ i = 1 m ∑ j = 1 n ∣ a i j ∣ 2 ) 1 2 \parallel A \parallel _{F}= \sqrt{tr(A^{H}A)}=(\sum_{i=1}^{m} \sum_{j=1}^{n} \mid a_{ij}\mid^{2} )^{\frac{1}{2}} ∥A∥F=tr(AHA)=(i=1∑mj=1∑n∣aij∣2)21
6.3 矩阵序列与矩阵级数
矩阵序列收敛

![]()
矩阵级数收敛

矩阵幂级数

★★★下面一个重要的定理

补充
P199 T18



https://blog.csdn.net/u013457167/article/details/54564393
P199 T19
七、矩阵函数
八、广义逆矩阵
行满秩 列满秩矩阵一些性质

A是 m × n m\times n m×n行满秩矩阵,所以行秩r(A)=m, A A T AA^{T} AAT是 m × m m \times m m×m矩阵,此时是满秩.列满秩情况类似可推导.


课堂只讲了广义逆矩阵 A + A^{+} A+ 与线性方程组的极小最小二乘解


通过以上可以得到求广义逆的两种方法:
(1) 奇异值分解

(2) 满秩分解

A = C + B + A=C^{+}B^{+} A=C+B+ , C + = C T ( C C T ) − 1 C^{+}=C^{T}(CC^{T})^{-1} C+=CT(CCT)−1 , B + = ( B T B ) − 1 B T B^{+}=(B^{T}B)^{-1}B^{T} B+=(BTB)−1BT
这个公式有对称的特征.
相容方程组
(1) 验证 A A + b = b AA^{+}b=b AA+b=b 是否相等,相等则 A x = b Ax=b% Ax=b 有解,则相容.
(2) 方程组 A x = b Ax=b Ax=b 有解, 则称该方程组是相容方程组.
rank(A) = rank(A b),相容
rank(A) 不等于 rank(A b),不相容
相容时
- 通解 x = A + b + ( I − A + A ) y x=A^{+}b+(I-A^{+}A)y x=A+b+(I−A+A)y
- 极小范数解 x = A + b x=A^{+}b x=A+b
不相容时
- 最小二乘通解 x = A + b + ( I − A + A ) y x=A^{+}b+(I-A^{+}A)y x=A+b+(I−A+A)y
- 极小最小二乘解 x = A + b x=A^{+}b x=A+b