详解Transformer中的Positional Encoding

参考：

1. https://arxiv.org/abs/1706.03762
2. https://www.zhihu.com/question/347678607
3. https://kazemnejad.com/blog/transformer_architecture_positional_encoding/#what-is-positional-encoding-and-why-do-we-need-it-in-the-first-place
4. https://blog.csdn.net/Datawhale/article/details/119582757?utm_medium=distribute.pc_aggpa

证明部分：

1. https://kazemnejad.com/blog/transformer_architecture_positional_encoding/#what-is-positional-encoding-and-why-do-we-need-it-in-the-first-place
2. https://timodenk.com/blog/linear-relationships-in-the-transformers-positional-encoding/

一、为什么要有Positional Encoding？

像论文中介绍的，由于Transformer中没有循环以及卷积结构，为了使模型能够利用序列的顺序，作者们需要插入一些关于tokens在序列中相对或绝对位置的信息。因此，作者们提出了“Positional Encoding位置编码”的概念。

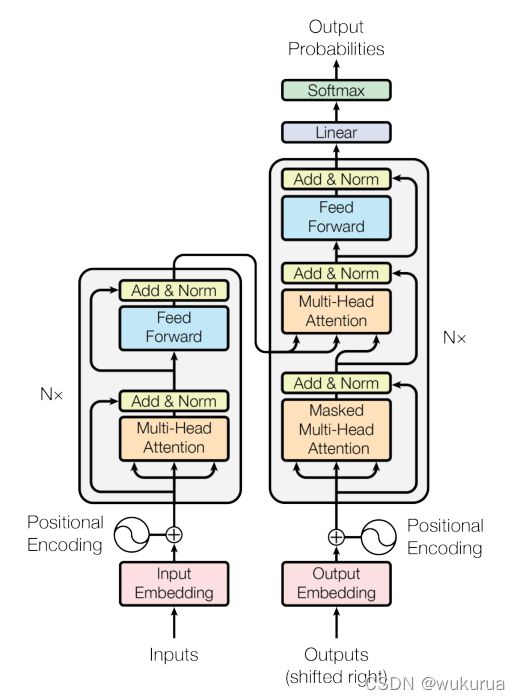
Positional Encoding和token embedding具有同样的维度，Positional Encoding和token embedding可以直接相加，结果作为Encoder和Decoder的底部输入。

二、怎么定义Positional Encoding？

现在知道我们需要Positional Encoding，那怎么定义它呢？

我们可以从头构思一下，直接编号行不？

直接编号

假设给定一个长度为 $T$ 的序列，token在序列中的位置记作 $pos$，那么token的位置编码
$$PE=pos=0,1,2,...,T-1$$
但是这就有个问题，如果有一段很长的序列（假如为1000），那么最后一个token的位置编码非常大，这是很不合适的：

1. 它比第一个token的编码大太多，和token embedding合并以后难免会出现特征在数值上的倾斜；
2. 它比一般的token embedding的数值要大，模型可能会把它当作主要信息，对模型可能有一定的干扰。

那么，位置编码最好具有一定的值域范围！

对每个位置 $pos$作归一化

我们可以使用序列长度 $T$ 对每个位置 $pos$ 作归一化，也就是$$PE=\frac{pos}{T-1}$$

上面两种方法都是建立一个长度为 $T$ 的词表，按词表的长度来分配position encoding，这两个方法都属于表格型。

这样固然使得所有位置编码都落入区间 $[0,1]$，但是问题也是显著的：
不同长度序列的位置编码的步长是不同的，在较短序列中相邻的两个token的位置编码的差异，会比长序列中相邻的两个token的位置编码差异更小。如果使用这种方法，那么在长文本中相对次序关系会被“稀释”。

我们关注的位置信息，最核心的就是相对次序关系，尤其是上下文中的次序关系。也就是关注一个token与另一个token距离的相对位置（距离差几个token）。应该让位置1和位置2的距离比位置3和位置10的距离更近，位置1和位置2与位置3和位置4都只相差1。

总结一下，position encoding的定义要满足下列需求：

1. 每个位置有一个唯一的positional encoding；
2. 最好具有一定的值域范围，否则它比一般的字嵌入的数值要大，难免会抢了字嵌入的「风头」，对模型可能有一定的干扰；
3. 需要体现一定的相对次序关系，并且在一定范围内的编码差异不应该依赖于文本长度，具有一定translation invariant平移不变性。

函数型

一种思路是使用有界的周期性函数。在前面的两种方法中，我们为了体现某个字在句子中的绝对位置，使用了一个单调的函数，使得任意后续的字符的位置编码都大于前面的字，如果我们放弃对绝对位置的追求，转而要求位置编码仅仅关注一定范围内的相对次序关系，那么使用一个sin/cos函数就是很好的选择，因为sin/cos函数的周期变化规律非常稳定，所以编码具有一定的平移不变性。如下：
$$PE(pos)=\sin \left(\omega \cdot pos\right)$$

其中，$\omega$ 越小，波长越长，即相邻的token的位置编码之间的差异越小。

但这样也存在一些问题：

1. 如果 $\omega$ 比较大，相邻token之间的位置差异不明显；
2. 如果 $\omega$ 比较小，在长序列中可能会有一些不同位置的token的位置编码一样，这是因为PE的值域 $[-1,1]$ 的表现范围有限。

既然token embedding的维度是 $d_{\text{model }}$（论文中$d_{\text{model }}=512$），那么也可以使用一个 $d_{\text{model }}$维向量来表示位置编码，这样的话，表示范围要远大于 $[-1,1]$ ，也方便后面和token embedding直接相加。

三、论文中的公式

论文中给出：positional encoding是一个向量，且${PE}_{pos}\in {\mathbb{R}}^{d_{\text{model }}}$，$f:\mathbb{N}\to {\mathbb{R}}^{d_{\text{model }}}$，${PE}_{pos}$ 定义为
$$\begin{array}{rl}P{E}_{(pos,2i)}& =\sin \left(pos/10000^{2i/d_{\text{model }}}\right)\\ P{E}_{(pos,2i+1)}& =\cos \left(pos/10000^{2i/d_{\text{model }}}\right)\end{array}$$

也可以写作：
$${PE}_{pos}^{(i)}=f(pos{)}^{(i)}:=\{\begin{array}{ll}\sin \left({\omega }_k\cdot pos\right),& \text{ if }i=2k\\ \cos \left({\omega }_k\cdot pos\right),& \text{ if }i=2k+1\end{array}$$

其中，$${\omega }_k=\frac{1}{10000^{2k/d_{\text{model }}}}$$

$i$ 表示 ${PE}_{pos}$ 的维度，$i$ 的取值范围是 $\left[0,\dots ,d_{\text{model }}/2\right)$。

具体描述

我们可以想象出这是一个由每一个频率产生的$\sin /\cos$对组成的向量（注意这里 $d_{\text{model }}$ 要除以 $2$ ）：
$${PE}_{pos}={\left[\begin{array}{c}\sin \left({\omega }_0\cdot pos\right)\\ \cos \left({\omega }_0\cdot pos\right)\\ \sin \left({\omega }_1\cdot pos\right)\\ \cos \left({\omega }_1\cdot pos\right)\\ ⋮\\ \sin \left({\omega }_{d_{\text{model }}/2-1}\cdot pos\right)\\ \cos \left({\omega }_{d_{\text{model }}/2-1}\cdot pos\right)\end{array}\right]}_{d_{\text{model }}\times 1}$$
论文说，频率沿着向量维度递减，波长 $10000^{2k/d_{\text{model }}}$ 呈几何级数增长，从从 $2\pi$ 增长到 $10000\cdot 2\pi$（不过我算着是到约 $9646.61612\cdot 2\pi$） 。
$${PE}_{pos}={\left[\begin{array}{c}\sin \left(pos/10000^{2\times \frac{0}{512}}\right)\\ \cos \left(pos/10000^{2\times \frac{0}{512}}\right)\\ ⋮\\ \sin \left(pos/10000^{2\times \frac{255}{512}}\right)\\ \cos \left(pos/10000^{2\times \frac{255}{512}}\right)\end{array}\right]}_{d_{\text{model }}\times 1}\approx {\left[\begin{array}{c}\sin \left(pos\right)\\ \cos \left(pos\right)\\ ⋮\\ \sin \left(9646.61612\cdot pos\right)\\ \cos \left(9646.61612\cdot pos\right)\end{array}\right]}_{d_{\text{model }}\times 1}$$

不过这样定义positional encoding，仍会陷入循环, 这里人为地将最大不重复序列长度限制为 512。例如，在 BERT 中就是这样做的（尽管值得一提的是他们使用了学习位置嵌入，但那是另一回事了）。 如果不这样做，模型确实无法区分序列中的第一个token和第513个token的位置编码。

四、为什么公式可以体现出相对次序关系？

1.相对次序关系怎么表示?

论文原文：

We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k, PEpos+k can be represented as a linear function of PEpos.

如果说Positional Encoding向量可以表示相对次序关系，那么 ${PE}_{pos}$ 应该满足 ${PE}_{pos+k}$ 是 ${PE}_{pos}$ 的线性变换，即：

对于任意固定的偏移量 $k$，存在线性变换 ${\mathbf{T}}^{(k)}\in {\mathbb{R}}^{d_{\text{model }}\times d_{\text{model }}}$，使得
$${\mathbf{T}}^{(k)}\cdot {PE}_{pos}={PE}_{pos+k}$$
这一等式对于序列中任何有效位置 $t\in \left\{0,1,\dots ,n-k-1\right\}$ 的任何位置偏移 $k\in \left\{1,\dots ,n\right\}$ 成立。

为什么满足这个公式，Positional Encoding向量就可以表示相对次序？

这里就谈到了对线性变换的理解，矩阵对向量的线性变换，其实是施加在其基底上的变换，而新的向量是关于新的基底的线性组合，与原来的向量关于原来的基底的线性组合，是一样的。是不是就可以对应上：新的向量 ${PE}_{pos+k}$ 是关于新的基底的线性组合，与原来的向量${PE}_{pos}$ 关于原来的基底的线性组合，是一样的。也就是说，他们之间的线性变换不受这个位置为 $pos$ 的token在序列中的绝对位置的影响，这个线性变换矩阵 ${\mathbf{T}}^{(k)}$ 可以表示出了不同距离的token的相对关系。

更多关于线性变换的直观理解：https://blog.csdn.net/xiaoyink/article/details/90705106

2.那论文公式满足这个相对次序关系的表示吗？

要使${\mathbf{T}}^{(k)}\cdot {PE}_{pos}={PE}_{pos+k}$，需要使 ${\mathbf{T}}^{(k)}$不依赖于 $pos$。

证明：

设 ${\mathbf{T}}^{(k)}$ 是一个 $2\times 2$矩阵， ${\mathbf{T}}^{(k)}=\left[\begin{array}{cc}{u}_1& v_1\\ u_2& v_2\end{array}\right]$，

则${\mathbf{T}}^{(k)}\cdot {PE}_{pos}={PE}_{pos+k}$可写作：
$$\left[\begin{array}{cc}{u}_1& v_1\\ u_2& v_2\end{array}\right].\left[\begin{array}{c}\sin ({\omega }_k\cdot pos)\\ \cos ({\omega }_k\cdot pos)\end{array}\right]=\left[\begin{array}{c}\sin ({\omega }_k\cdot (pos+\varphi ))\\ \cos ({\omega }_k\cdot (pos+\varphi ))\end{array}\right]$$
等式右边使用三角函数正余弦公式，可化为：
$$\left[\begin{array}{cc}{u}_1& v_1\\ u_2& v_2\end{array}\right].\left[\begin{array}{c}\sin ({\omega }_k\cdot pos)\\ \cos ({\omega }_k\cdot pos)\end{array}\right]=\left[\begin{array}{c}\sin ({\omega }_k\cdot pos)\cos ({\omega }_k\cdot \varphi )+\cos ({\omega }_k\cdot pos)\sin ({\omega }_k\cdot \varphi )\\ \cos ({\omega }_k\cdot pos)\cos ({\omega }_k\cdot \varphi )-\sin ({\omega }_k\cdot pos)\sin ({\omega }_k\cdot \varphi )\end{array}\right]$$

可以得到以下两个等式：
$$\begin{gathered} u_1\sin ({\omega }_k\cdot pos)+v_1\cos ({\omega }_k\cdot pos)=\cos ({\omega }_k\cdot \varphi )\sin ({\omega }_k\cdot pos)+\sin ({\omega }_k\cdot \varphi )\cos ({\omega }_k\cdot pos) \\ {u}_2\sin ({\omega }_k\cdot pos)+v_2\cos ({\omega }_k\cdot pos)=-\sin ({\omega }_k\cdot \varphi )\sin ({\omega }_k\cdot pos)+\cos ({\omega }_k\cdot \varphi )\cos ({\omega }_k\cdot pos) \end{gathered}$$

求解上述方程，得到：

$$T_{\varphi ,k}=\left[\begin{array}{cc}\cos ({\omega }_k.\varphi )& \sin ({\omega }_k.\varphi )\\ -\sin ({\omega }_k.\varphi )& \cos ({\omega }_k.\varphi )\end{array}\right]$$
即 ${\mathbf{T}}^{(k)}$ 不依赖于 $pos$。
而且可以发现，${\mathbf{T}}^{(k)}$ 跟旋转矩阵很相似。