《PWC-Net：CNNs for Optical Flow Using Pyramid,Warping,and Cost Volume》论文笔记

参考代码（official）：PWC-Net
参考代码（pytorch convert）：pytorch-pwc

1. 概述

导读：这篇文章给出了一种使用CNN网络实现光流估计的方法，在该方法中采用了经典的特征金字塔结构作为特征提取网络。之后在金字塔的某个层级上使用上一级的光流作为warp引导，第二幅图像的特征将被warp。进而使用第二幅图像warp之后的特征和第一幅图像的特征构建一个cost volume。在此基础之上，添加一个估计网络从而实现当前金字塔层的光流估计。文章的方法简单明了，在模型的体积上和infer时间上分别比FlowNet2小了17倍和2倍，并且相比FlowNet2繁琐的训练过程文章的方法训练起来更加容易。

将文章的方法与之前的一些光流估计网络进行infer时间与参数量上的比较：

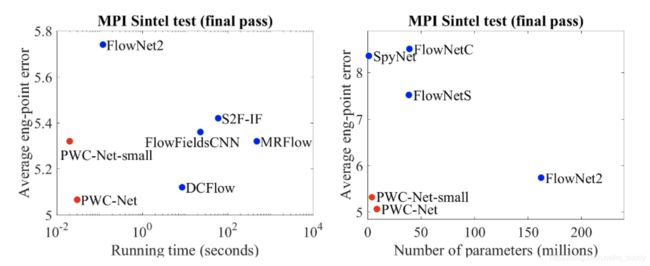
2. 方法设计

2.1 网络结构

文章方法的网络结构见上图的右图所示，其输入的图像表示为$I_1,I_2$，经过共享权重的CNN网络进行特征抽取（生成的特征描述为$feat=[c_t^1,c_t^2,c_t^3,c_t^4,c_t^5,c_t^6]$，其中$t$为图像的索引值），之后在$stride=[2,4,8,16,32,64]$的特征上进行迭代优化（这里的$channel=[16,32,64,96,128,192]$）生成最后的光流估计，最后会使用传统的中值滤波或是双边滤波作后处理得到最后的光流结果。

2.2 网络模块

特征warp操作：
这里使用上一层特征生成的光流估计对当前图像2特征进行warp操作，从而对几何形变进行补偿以及使得图像块在正确的尺度上，其warp的过程可以描述为：
$$c_w^l(x)=c_2^l(x+u{p}_2(w^{l+1})(x))$$
其中，$x$是像素的索引，$u{p}_2(w^{l+1})$是上采样之后的光流估计结果，$w^{l+1}$是上一个层的光流估计结果。

cost volume构建：
文章的cost volume采用的是在窗口内向量乘积的形式，这里的窗口大小指的是输入的两个图像相对移动的范围，表示为$|x_1-x_2{|}_{\infty }\le d$。则cost volume的计算描述为：
$$c{v}^l(x_1,x_2)=\frac{1}{N}(c_1^l(x_1){)}^T{c}_w^l(x_2)$$
其中，$N$是列向量$c_1^l(x_1)$的数量。生成的cost volume的维度为$d^2\ast H^l\ast W^l$。

光流估计模块：
这里是用生成的cost volume作为输入，之后接几个卷积从而得到光流估计结果。

context优化模块：
这部分网络是在金字塔网络的最后添加的，主要是添加了几个膨胀卷积用以增大感受野，其膨胀系数设置为$ratio=[1,2,4,8,16,1,1]$。

2.3 损失函数

训练的时候文章使用L2损失：
$$L(\theta )=\sum _{l=l_0}^L{\alpha }_l\sum _x|w_{\theta }^l(x)-w_{GT}^l(x){|}_2+\gamma |\theta {|}_2$$
而在finetune训练阶段文章使用的L1损失：
$$L(\theta )=\sum _{l=l_0}^L{\alpha }_l\sum _x|w_{\theta }^l(x)-w_{GT}^l(x)+\eta {|}^q+\gamma |\theta {|}_2$$

3. 实验结果

Sintel benchmark：

KITTI：