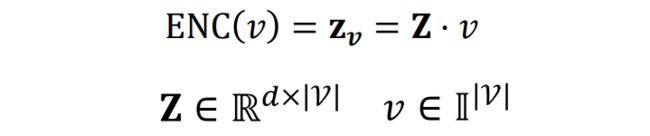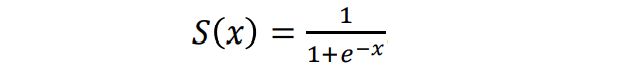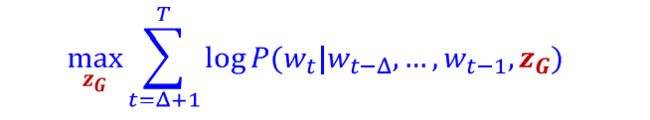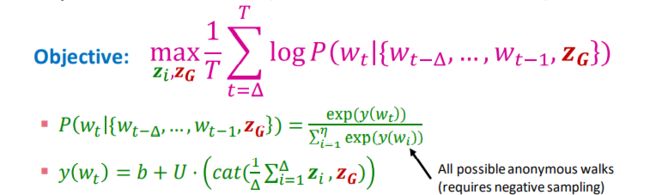【斯坦福大学公开课CS224W——图机器学习】三、节点和图嵌入

【斯坦福大学公开课CS224W——图机器学习】三、节点和图嵌入

1. 节点嵌入

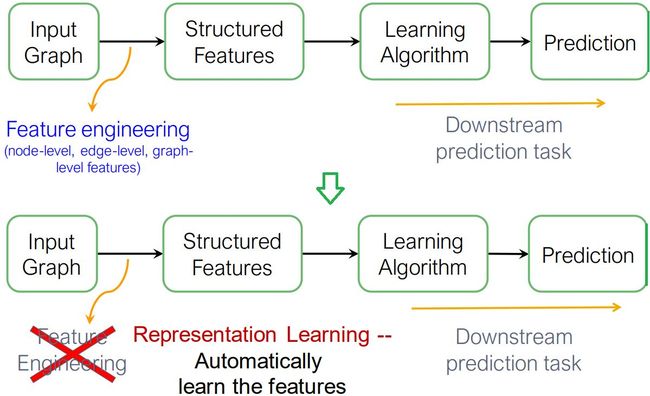
在传统的图机器学习中，将图数据作为模型的输入，再进行特征工程，从图中获取结构特征，之后将特征表示用于下游任务中。这样的设计流程（如下图所示）存在着一定的问题，即对于每一个新的图任务，我们需要重新为其设置特征，同时在一般情况下，特征工程比较耗时，获取的特征也不一定能准确地表示图数据，于是，便有了利用自动学习特征的方式来替换原有特征工程的思想。

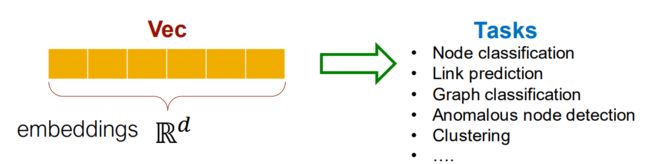
在自动特征学习的思想基础上，现在的目标在于使用图进行机器学习，并做到高效任务无关的特征学习。在这方面，一种自动特征学习的做法是，通过某一映射函数，将图结构信息自动表示成低维向量，且这种低维向量包含了图结构的信息，这个过程称为嵌入（Embedding）。

在上图中显示的是节点嵌入（node embedding）的过程，即将输入的图中的每一个节点表示成一个低维向量的过程，而将节点映射到成低维向量的好处在于这样的表示能够很好地被输入到下游任务中，在保持设计流程不变的情况下，完成特定的图任务。

另外，如果图中两个节点在结构信息上具有一定的相似性，那么在低维空间中主要体现在向量的空间紧密关系上，比如在提出DeepWalk模型的论文中，作者将实验结果可视化后，这种紧密关系可以被很好地体现出来，具体的论文插图如下图所示。

1.1 编码器与解码器

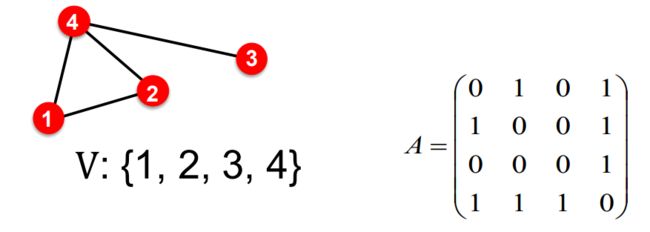
现假设存在一个图G，用V表示顶点集，用A表示邻接矩阵（其中元素为1表示两个节点之间相连接，元素为0表示互不相连），为了简化问题，这里只使用现有的信息，而不考虑其他节点信息和特征。

节点嵌入的目标是寻找一个方法将节点映射到嵌入空间（前文提及的低维空间），这一过程称为编码过程（encode），而这个方法称为编码器（encoder）。在编码过程中，需要确保原始图中节点相似性能在嵌入空间中得以体现。

而为了确保映射后相似性仍然存在，对于映射到嵌入空间的节点表示（低维向量），需要找到一个方法来衡量两个低维向量的相似性，即将两个低维向量映射到它们之间的相似得分上（similarity score），这个过程称为解码过程（decode），这个方法被称为解码器（decoder），上图中以向量内积（dot-product）为例。

根据前文的分析，目前对于节点嵌入的过程，可以归结为以下四个步骤：1）建立编码器（找到一种将节点映射到低维空间的方法）；2）建立解码器（找到一种将低维向量映射到相似得分的方法）；3）定义原图空间中节点的相似度（模型优化的方向是解码器计算得到的相似得分与原图中两个节点的相似度尽可能相等）；优化编码器的参数，使得原图中节点相似度尽可能与解码器求得的相似度保持一致。

为了说明建立编码器的过程，现在以一个简单的编码过程为例。这种方法需要事先建立一张嵌入向量表，而这里的编码器只是一个嵌入查找（embedding-lookup），对应的查找公式如下：

其中，Z是一个矩阵，Z的每一列表示一个节点的嵌入，Z的行数d表示嵌入的空间维度，v是指示向量，除表示节点 v 的列中为 1 外其余全为零，即利用向量v可以求出对应节点v的embedding。

在这种编码过程中，每一个节点都事先被表示成一个独一无二的嵌入向量，而模型训练的过程就是优化这个向量表示的过程。这种学习嵌入的方法包括DeepWalk和node2vec模型，但是这种编码过程有一个明显的缺点，即如果节点很多时，需要为每个节点都维护一个对应的嵌入向量，开销较大。这也是后来出现了深度编码器（Deep encoder——GNNs）的一个原因。

然而，在前文的描述中，仍然存在着一个需要解决的问题，即原图中节点的相似性需要如何被定义，是以是否相连来定义？还是以是否有共同的邻居来定义？或者是以某些结构相似规则来定义？针对这个问题，本文将使用随机游走（random walks）的节点相似性来定义，在后文中将讨论如何针对这种相似性度量优化嵌入。同时，需要注意的是以这种方式来学习节点嵌入是一种无监督或自监督（unsupervised/self-supervised）方式，因为在这个过程中不需要使用节点标签。

1.2 节点嵌入的游走策略

前文中提及的原图节点相似度衡量问题，一种思路是通过游走策略来生成节点序列（在图中从一个节点出发进行游走，并记录下游走经过的节点），然后通过在序列中两节点是否同时出现来作为衡量节点相似度的标准，这里的游走策略可以是随机游走（DeepWalk），也可以是依据某种策略来游走（node2vec）。而在进入游走策略的学习前，首先需要先定义一些符号：

• 节点u的嵌入向量

• 以节点u作为游走起点，访问节点v的可能性

• Softmax函数

• Sigmoid函数

（1）随机游走策略

给定一个图和一个起点，我们随机选择它的一个邻居，并移动到这个邻居；然后我们在当前节点继续随机选择一个该节点的邻居，并移动到这个节点，如此循环至序列达到一定长度后结束，以这种方式访问节点的策略称为随机游走。

使用随机游走策略的好处在于：1）从表达性上看，灵活随机的节点相似度定义包含了局部和高阶邻域信息，其思想是如果从节点 开始的随机游走以高概率访问 ，则 和 相似（高阶多跳信息）；2）从效率上看，训练时不需要考虑所有节点对，只需要考虑随机游走中同时出现的节点对。

在随机游走策略中，给定图G=(V,E)，其中V表示节点集，E表示边集，我们的目标是学习一种映射f，使得节点能准确映射到低维向量空间，在这个问题中，我们优化的目标是：

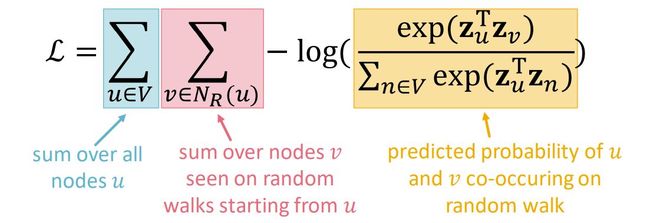
根据优化目标，结合Softmax函数，我们可以为游走算法设计一个损失函数L，其表达式为：

从表达式中可以发现一个问题，即计算的时间复杂度会很高，因为在log部分的分母中，需要计算所有的节点对，因此，解决这一问题，这里使用了负采样（Negative sampling）的方法来替代log部分：

在上式中，负样本数k的选择一般为k=5-20，且为了效率，在实际中经常采用任何节点，然而，最“正确”的方式是采用不在walk 上的节点。另外，在模型的训练过程中，主要采用随机梯度下降法（Stochastic Gradient Descent）来进行优化。

（2）node2vec

node2vec模型与DeepWalk模型的区别在于node2vec模型使用的游走策略不是单纯的随机游走策略，而是使用灵活的、有偏的随机游走，这种策略可以在网络的局部视图和全局视图之间进行权衡。

利用深度优先搜索（DFS）进行全局节点信息的访问，利用广度优先搜索（BFS）进行局部节点信息的访问，在这个过程中，需要设置两个概率参数来决定游走的策略：

• • Return参数p（从当前节点访问前一个访问节点的概率）
  • In-out参数q（用于选择BFS或DFS）

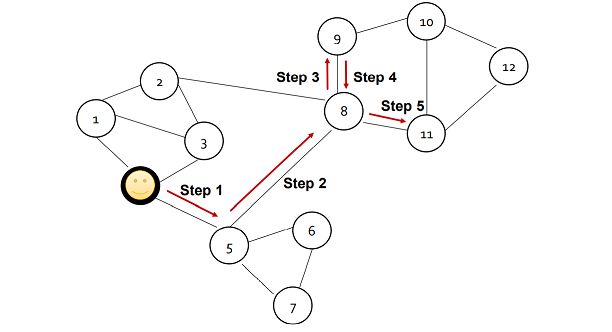
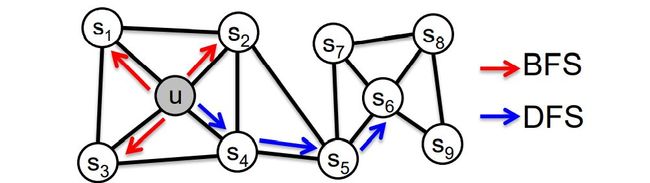
这种游走策略也称为二阶随机游走策略（second-order random walks），因为这种游走策略在选择节点时考虑了过去访问的节点信息，其具体的游走过程如下图所示：

当位于节点w处时，有1/p的可能返回已经访问过的节点S1，也有1/q的可能访问与起始节点u距离更远的节点S3和S4，同时也可能访问与起始节点u距离相同的节点S2。其中，当p的取值较低时，游走偏向于BFS-like walk，当q的取值较低时，游走偏向于DFS-like walk。

2. 图嵌入

在前文的论述中，主要围绕节点嵌入展开，现在将对完整的图嵌入进行讨论。而之所以希望对图进行嵌入，是因为有时可能需要对图进行分类，比如判断整个分子（由原子构成）是否具有毒性这样的任务，接下来将介绍几种可行的方法。

2.1 Approach 1

一种简单的图嵌入思想是在节点嵌入的基础上，利用节点嵌入向量相加后得到图嵌入向量，这种方法对应的公式如下：

2.2 Approach 2

第二种方法的思想是引入“虚拟节点”（virtual node）来表示（子）图并进行节点嵌入操作，之后获得整个“虚拟节点”的向量表示，以此向量来表示图。

2.3 Approach 3

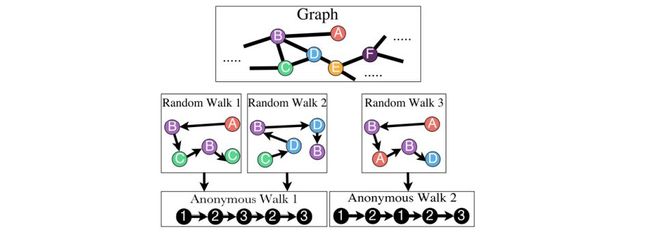
第三种方法是匿名游走嵌入（Anonymous Walk Embedding），匿名游走中的状态对应于我们第一次访问随机游走中的节点的索引，以论文Anonymous Walk Embeddings中的插图为例：

对于上面的图，随机游走策略可能会生成三种游走序列，对于三种游走序列，我们将序列中的节点匿名化，比如Random Walk 1，第一个节点是A，则将A映射为索引1，之后出现节点A的地方就用1代替，第二个节点是B，则将B映射为索引2，之后出现节点B的地方就用2代替，对于Random Walk 2和Random Walk 3 的分析同理。那么对于节点总数为n，游走序列长度为m（m

比如游走序列长度为3时，匿名序列有5种，分别是w1 = 111，w2 = 112，w3 = 121，w4 = 122，w5 = 123。匿名游走策略的思想是模拟 步的匿名游走 并记录他们的计数，将图表示为这些游走的概率分布。比如上面的例子中， = 3，则我们可以把图嵌入到一个5维空间中（即用5维的向量表示），其中，其中，第i维的值表示匿名游走wi在图中出现的概率，即：

对于上面这个方面，我们需要采样多少次随机游走序列呢？在Anonymous Walk Embeddings这篇论文中，作者给出了一个计算采样次数m的计算公式，如果希望分布的误差大于 时的可能小于 ，则计算公式为：

其中： 是长度为 的匿名游走的步行总数，比如上面 = 3时， = 5。之后作者在这一思想的基础上，提出了一种通过匿名游走 来学习嵌入的方法。这种方法在学习所有匿名游走 的同时也学习图的嵌入。

这种Learn Walk Embeddings的思想具体实现是这样的：这里以node1作为匿名随机游走采样的起始点，现在我们先采样4次，可得到如下图的游走序列：

之后我们预测在 大小的窗口中同时发生的游走序列，比如，给定w1，w2游走序列和初始的图嵌入，预测w3出现的概率，对应的目标函数为：

上面的描述是采样数为4的情况，现在假定采样数为T，起始节点为u，游走步长为l（即有T个以节点u为起点步长为l的游走序列），并设预测的窗口大小为 ，同时初始化图嵌入向量，则对应的目标函数为：

其中，cat操作是将窗口中的匿名游走向量求平均值，再与图嵌入向量进行拼接操作，参数b和参数U是需要学习的参数。这个方法对应的整体流程如下：