ironpython使用opencv_一起学opencv-python三十七（视频分析：光流）

光流

参考了https://blog.csdn.net/jobbofhe/article/details/80448961

https://my.oschina.net/u/3702502/blog/1815343

和https://blog.csdn.net/qq_38906523/article/details/80781242

和https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_video/py_lucas_kanade/py_lucas_kanade.html#lucas-kanade

亮度就是灰度值或者BGR通道的值，这个值不完全发生变化是不太可能的。

下面的Lucas-Kanade就是基于梯度的方法，基于匹配的方法问题其实上一讲也说过，如果我们要检测的特征点的匹配效果很差，那么光流的效果就会很差，，这个其实就是因为光流太稀疏，就是特征点太少导致的。

上面是对光流的一些简单介绍。下面就稍微来展开说一说。

也就是说，上一帧在x,y处的点现在到了x+dx,y+dy处，经过了dt时间，上式之所以可以舍弃二二阶以上的高阶项，就要满足运动微小假设。

上面给出了求u的一种方法。这种方法叫做Lucas-Kanade方法。用的其实就是最小二乘法。里面Ix,Iy就是图像在（x,y）点的梯度分量，It的话，就拿后一帧的(x,y)处的亮度减去前一帧的，然后帧之间的时间我们是知道的。

这里我再说说第三个条件，空间一致性的意思，其实说的意思是：比如我们要同时跟踪的是两只鸟，但是这两只鸟一只向左飞，一只向右飞，那最后得到的结果肯定是很奇葩的。就像上面的两个蓝点，它们不能同时作为跟踪的对象。

补充：http://blog.sina.com.cn/s/blog_50363a7901011215.html

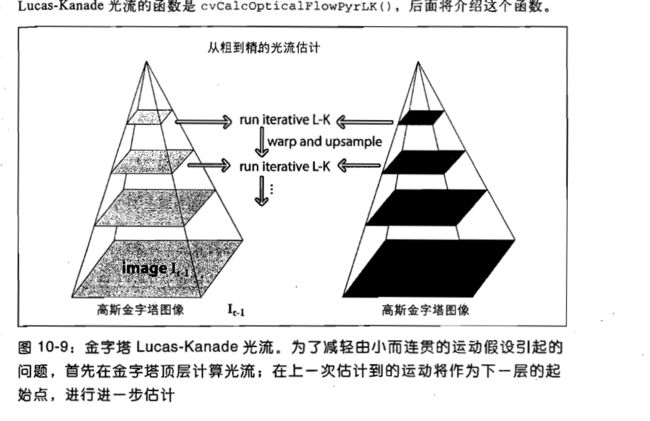
这个W我们还是一般用高斯或者其它的核，这个和meanshift的思想一样，就是为了减少噪声的影响。上面我们讨论的都是在小运动的情况下，但是如果有比较大的运动呢，所以我们用了金字塔，当我们使用图像金字塔的时候，小运动会被消除，这个我想应该是先缩小图片，然后再放大，用的是这个过程吧，这样的话，确实几乎看不出来小运动，但是这样能把大运动变成小运动？我还是比较存疑的，这里的大运动应该指的也不能是很大范围的运动吧。

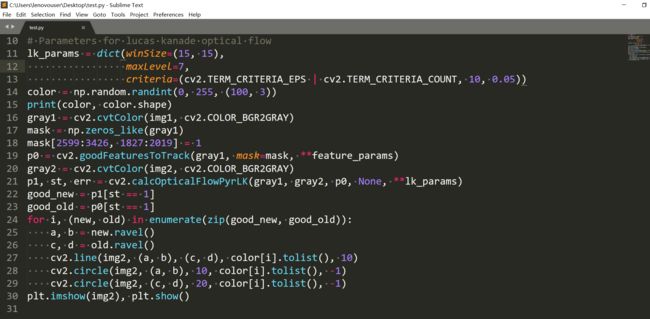
opencv中有函数,calcOpticalFlowPyrLK()可以用来做光流分析，其实光流法也是用于目标追踪的一种方法。首先我们需要指明需要跟踪物体的特征点，例子用的是Shi-Tomasi方法检测的，然后我们就用光流法来跟踪这些点。这里只用了一次特征检测，就是第一帧的时候或者预备帧的时候，第二帧的时候特征点的位置不是靠特征检测，而是根据Lucas-Kanade光流法计算出来的偏移量直接移动的，那么其实这样的误差是会累积的。这个函数里，输入参数有前一帧，后一帧，前一帧中特征点坐标。返回的是后一阵中的点，还有一些状态数，如果状态数为1，表示下一帧的点找到了，如果是0，则没有找到。我们先来看看这个函数：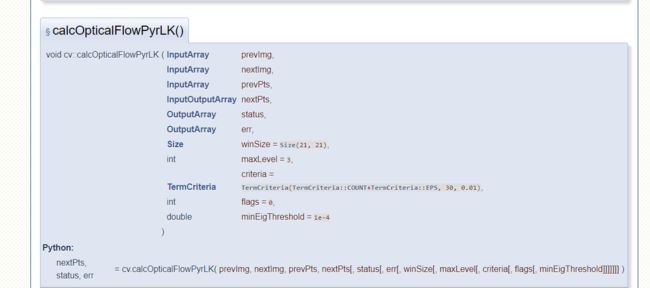

参数蛮多的，参考https://blog.csdn.net/qq_29541381/article/details/80154329

这个minEigThreshold参数的设立就是为了过滤调一些不好的特征点，虽然前面特征检测都已经过滤过了。这个矩阵指的是：

看到这个函数的输入参数，感觉其实有点懵逼。这个我还真的满看出来哪里用了迭代。这里推荐《学习opencv》这本书，里面对很多方法都有详细的介绍，下载方法在https://www.linuxidc.com/Linux/2011-08/39907.htm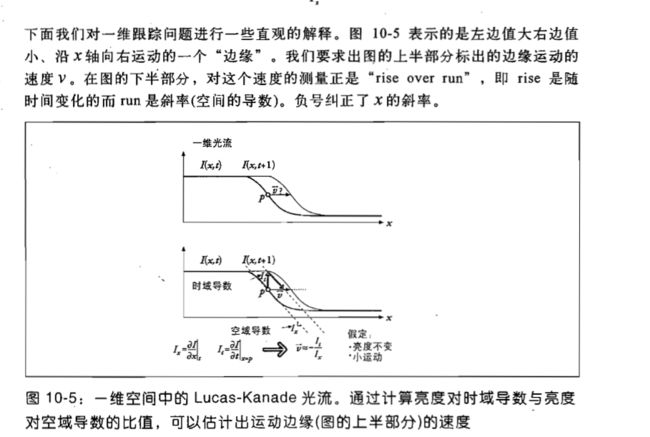

这个是一个一维的例子。

这里我们就看到了用牛顿法迭代的过程了，这个解决了亮度不变这个假设不能满足的问题，虽然可能结果并不收敛，所以说会出现找不到下一帧对应点的情况啊。

也就是说会对原图进行降采样，缩小图片大小，这样的话想想的确可以把大运动变成小运动，因为中间差的像素数少多了，原来可能差4个像素，一变小就差2个了。

先从小的图片开始用光流法，因为它容易满足小运动的假设。

这样稍微大一点的运动我们也能处理了。

这本书真的很不错呢，把原理都讲得很清楚，我很喜欢。真的是为什么不早点找这本书，这样查资料就不用那么费时了，左查一点，右查一点。opencv代码：

看到有人问我要代码，其实代码这些教程网站上都有啊。我还是只用两张图片(原来的眼镜清洗液的图片)来测试，其中修改了部分代码：

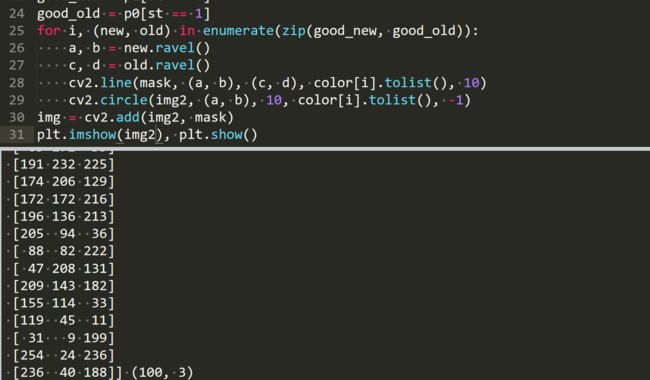
我在特征检测哪里加了掩模，只希望检测眼镜清洗液的特征点。color = np.random.randint(0, 255, (100, 3))是来产生随机颜色的，范围是在0,255之间，形状是100*3。zeros_like函数参考

https://blog.csdn.net/wuguangbin1230/article/details/72850333

返回的是和输入数组一样形状和数据类型的数组，不过元素都是0。

结果：

效果并不好，我来看看图一里面特征点检测得怎么样：

这个检测得其实挺好的嘛。

看来需要改一些参数呢，

不过效果还是不好呢，

那些比较大的点是前一帧中的特征点，小的点是这一帧的特征点，这次的点都偏左，而上次是偏右。金字塔的层数会是一个比较关键的参数，如果太小，可能即使降采样也不符合小运动，所以这个参数尽量大一些。

这个结果其实挺不错了。

其它参数不变，加大金字塔层数，结果反而更差了，这是因为每次降采样都要丢失信息，如果降采样次数太多，会连特征点的特征信息都被丢弃了，所以说金字塔层数要选择合适，不能太大也不能太小。

稠密光流

不过这两种方法似乎已经被opencv舍弃了，至少3.4.2里面我没找到这几个函数，好吧原来上面那本书是基于opencv1的。上面的Lucas-Kanade光流方法的特征点用的比较少。opencv还提供了另外一种算法来找到稠密光流，它计算这一帧的所有点的光流，用的方法是基于Gunner Fareback的算法，这种算法用的是基于多项式展开的两帧运动估计。

好吧，我重新找了学习opencv3的电子书，不过没找到中文版的。看一下里面对这个calcOpticalFlowFarneback方法的描述：

多项式展开算法基于把图像估计为一个连续平面的分析技术来尝试计算光流。当然，真正的图像是离散的，所以Farneback方法添加一些额外的复杂度来让我们可以把基本方法应用到真正的数字图像中去。Farneback算法的基本思想是在图像的每个点用分段多项式拟合的方法来估计图像（虽然我感觉应该是插值啊，但是用的是fit这个单词）。

这个算法的名字是从算法的第一步操作得来的，第一步是用二次多项式在每个点附近进行拟合。多项式是基于点附近的窗口来估计的，这个窗口的每个位置有相应的权重，这是为了让拟合对离窗口中心的点更敏感。所以，窗口的尺度决定了算法敏感的特征的尺度。理想情况下，图像可以按照光滑连续函数来对待。

如果把图像中两个位置的像素值互换，会导致在同一点多项式展开系数的变化。从这个变化

我们可以计算得到这个置换导致的一个幅值。当然，这对点的互换应该位置比较近才有意义。然而，有一个技巧可以处理很远的互换。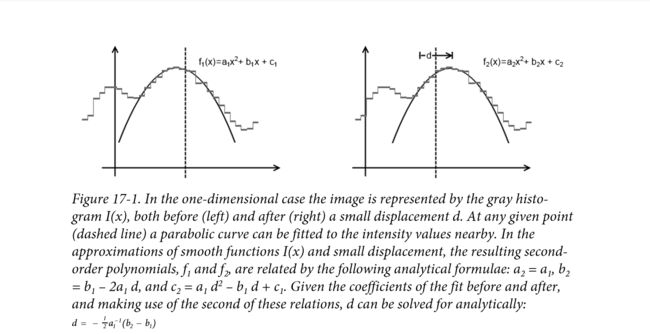

一维情况下：左边到右边的图，只是稍微换了一下中心点，中心点位置用虚线标出，两张都用二次曲线拟合，离中心点越近的点，和拟合出来的二次曲线越契合。由于中心点的移动，二次曲线发生了变化，系数关系是：a2=a1，b2=b1-2a1*d,c2=a1*d^2-b1*d+c1。d是中心点移动的距离。用这些关系，可以解出关于d的表达式，见上图。

关于这个技巧，首先，如果你知道一些有关这个置换的信息，也就是我们可以预估一个光流，那么你可以不在同一个点比较两幅图像的拟合系数，可以在那些你预估的地方比较。这种情况下，根据上面的分析技术，我们可以计算出一个比较小的修正值来修正预估值。实际上，这种机制有助于减少迭代次数。这种方法其实用于比较远的点的置换。其实还是用图像金字塔，先用分辨率比较低的，降采样很多次的结果，然后在用上一层降采样的结果。和上面Lucas-Kanade用金字塔的方法一样。

参数含义参考https://blog.csdn.net/ironyoung/article/details/60884929

4就是每次缩小的宽高的倍数，0.5是典型值，8就是每个窗口的权值要用的高斯分布参数，

关于flags，上面一种是用输入的作为估计值，下面是用高斯核对原来的估计值的窗口那里滤波一下，这种方法比较慢，高斯窗口的值要大一些为了保证鲁棒性。用例子中的参数，修改层数为6，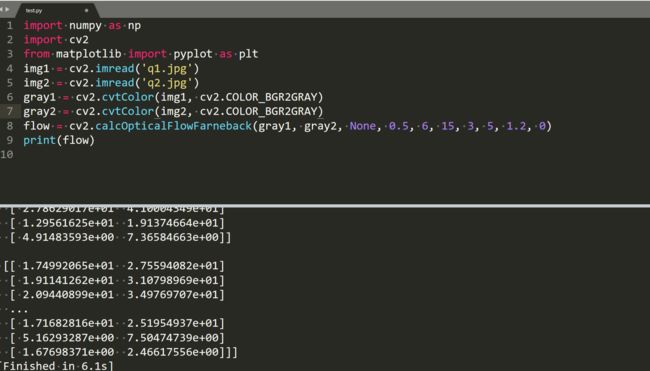

这个确实很花费时间。flow就是从上一帧到这一帧每个点对应的移动距离。

mag, ang = cv2.cartToPolar(flow[...,0], flow[...,1])

cartToPolar就是从直角坐标转极坐标的函数，以前也见过的，输出是幅值和相角（默认是弧度）。

hsv[...,0] = ang*180/np.pi/2

hsv[...,2] = cv2.normalize(mag,None,0,255,cv2.NORM_MINMAX)

rgb = cv2.cvtColor(hsv,cv2.COLOR_HSV2BGR)

opencv这么处理是为了可视化，这样的话，颜色就代表移动的方向，ang是弧度，需要转成角度，然后亮度代表移动的速度，这种处理还是比较好的一种方式。

例子里面，这个应该是用摄像头拍的，周围的景色不东，所以是黑色，这三个人的运动方向不同，所以颜色不同，亮度代表运动速度。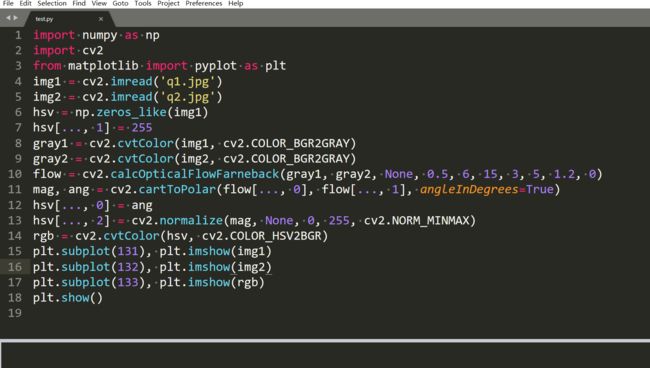

结果：

其它还有很多光流法和目标跟踪方法，这里不在介绍，都在第17章里面。