[论文阅读笔记17]MAT: Motion-Aware Multi-Object Tracking
前言:
论文地址: 论文
对于tracking-by-detection范式的MOT算法而言, 改进的重点在于目标特征的提取, 表示和关联策略上. 之所以做这篇文章的笔记, 是这篇文章在这些方面都做了改进, 针对相机运动和目标非刚性运动造成的运动特征不稳定, 针对目标长时间消失再匹配问题和轨迹平滑问题都做了改进, 并且提出了一种循环关联策略, 内容还是很充实的.
\space
1. Introduction
在引言部分. 作者重点交代了tracking-by-detection存在的问题, 正如前言部分所说. 后面论证了依靠外观特征的一些缺点, 例如依赖高精度检测, 耗时计算量大, 当目标相似或模糊的时候不稳定等. 进而提出为什么这篇文章用motion-aware, 一是外观特征不稳定, 二是运动特征就足够好.
文章的创新点主要是:
- 针对相机运动和目标非刚性运动问题, 提出了一个集成运动定位(Integrated motion localization, IML)模块
- 针对长期遮挡后目标重连接问题, 提出了一个轨迹平滑模块, 叫做动态重连接上下文(Dynamic reconnection context, DRC)
- 对于关联阶段, 利用** 3D integral image(3DII)**模块来去除多余的轨迹和检测的关联.
下面分别进行说明.
\space
2. 集成运动定位(Integrated motion localization, IML)
解决相机运动或者目标非刚性运动造成的Kalman恒定速度假设失效问题, 作者说大致有两种解决方式. 1. 对极几何, 但是对极几何在求解基本矩阵的时候要进行图像的特征点匹配, 然而图像的特征点往往分布在梯度信息丰富的地方, 也就是更容易分布在目标本身. 因此作者采取第二种: 2. 求解仿射变换, 借鉴了一篇08年的文献, 也是基于图像配准问题求解出仿射矩阵.
实际上, 这部分和BoT-SORT非常想象, 而且BoT-SORT为了解决特征点分布在目标本身, 在求解图像特征点的时候把目标扣去了, 比这个聪明一点.
与BoT-SORT相同, 得到仿射变换后修正Kalman的结果:

其中 w r a p ( ⋅ ) wrap(·) wrap(⋅)表示仿射变换, F , Q , P , s F, Q, P, s F,Q,P,s分别是状态转移矩阵, 噪声矩阵, 状态向量的协方差矩阵和状态向量.
\space
3. 动态重连接上下文(Dynamic reconnection context, DRC)
该部分有两个工作, 一是决定丢失轨迹动态存活时间(寿命)的基于运动的动态重连接机制, 二是轨迹平滑的循环伪观测轨迹填充.
3.1 基于运动的动态重连接机制
作者说, 在拥挤和目标相互遮挡的情形, 靠Re-ID是不可靠的. 怎么办呢? 当目标丢失的时候, 我们仍对它的状态进行预测, 以便将来某一帧再去恢复它. (其实其他的算法在实现上都是这么做的, 在轨迹inactive后, Kalman滤波依旧保持更新). 但是我们知道的是, 当轨迹没有观测(检测)的时候, Kalman的方差是会越走越大的(证明参见OCSORT). 然而这个工作不同之处是, 基于相机运动和目标非线性运动的程度, 动态地决定目标存活的时间.
于是针对每一个inactive的轨迹, 存活时间定义为:

其中, L m a x L_{max} Lmax为常数, 指最大存活时间. α \alpha α为系数, V b o x V_{box} Vbox为Kalman状态向量中bbox的速度(本工作状态向量表示为边界框及其导数, 即 x = [ b o x , V b o x ] ∈ R 8 x=[box, V_{box}]\in\mathbb{R}^8 x=[box,Vbox]∈R8). I c a m I_{cam} Icam指相机运动的强度, 按下式计算:

其中 W W W是第一个模块IML求解出的仿射矩阵, R R R是单位矩阵和零矩阵拼接成的矩阵. 因为论文中没有给 × \times ×的含义, 我们可以先把 I c a m I_{cam} Icam的公式的第二部分理解成余弦相似度, I c a m I_{cam} Icam即为1-余弦相似度. 我们知道, 仿射矩阵包含两部分(参见BoT-SORT), 一是旋转矩阵, 二是平移向量. 如果不发生任何的变化, 则仿射矩阵与 R = [ I ; O ] R= [I;O] R=[I;O]相同(即不旋转缩放, 也不平移). 如果旋转和平移的程度越大, 则 W W W和 R R R的相似度就会越低. I c a m I_{cam} Icam的值就会越大.
同样, 若边界框运动的越快, 则 V b o x V_{box} Vbox越大. 综上, 如果 I c a m I_{cam} Icam和 V b o x V_{box} Vbox越大, 则 L r e c L_{rec} Lrec就会越小. 也就是说, 作者给予运动不确定性更高的目标更小的存活寿命.
3.2 轨迹平滑的循环伪观测轨迹填充
当轨迹要恢复的时候, 我们知道Kalman滤波这时候误差已经大了很多了. OCSORT为了解决这个问题, 在目标消失处和再发现的地方建立了一个线性的虚拟轨迹来修正Kalman, 这里作者用了一个更复杂的策略来平滑轨迹.
![[论文阅读笔记17]MAT: Motion-Aware Multi-Object Tracking_第1张图片](http://img.e-com-net.com/image/info8/0199d4a29eb341c9a03415f82b75666f.jpg)
按照上图, 将过程做一个分解. 假定A为轨迹消失的地方, B为轨迹重新发现的地方.
- 根据AB的位置在中间帧对归集的位置和bbox大小线性填充, 这里的行为应该和OCSORT相似. 线性填充如蓝线所示.
- 利用IML模型从A点更新到B点, 也就是Inertia IML的紫色轨迹
- 利用IML模型从B点反向推理到A点, 并和第2步结合, 得到filled trajectory, 即黄色轨迹
可以看出, filled trajectory通过线性轨迹为基础, 经过双向IML平滑得到的. 因此比只利用Kalman(灰色轨迹)好很多.
\space
4. 3D集成图像模块(3D Intergal image, 3DII)
该部分解决的问题是, 当目标数量多的时候cost matrix的冗余计算问题. 因为这时候cost matrix会变得很大, 而作者的观点是不需要这么大, 因为有些detection-track对是可以舍弃的.
怎么舍弃呢? 其实还是根据位置的先验信息进行一个排除.
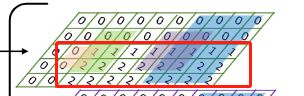
对于第 t t t帧图像, 我们把图像划分成 M × N M\times N M×N个网格, 假设有 m m m个detections, 我们就弄出 m m m层网格图, 在detection对应的位置上分别把网格的值给1, 否则给0:
![]()
比如对于Det1图, 有两个位置是1, 也就是说, 新图 I 3 D I_{3D} I3D的 ( m , n ) (m,n) (m,n)位置, 是原本 ( m , n ) (m,n) (m,n)位置左上角的所有值的和, 因此就得到了:
当然, 求解这个式子太麻烦了, 因为计算每个网格的时候, 存在着重复计算. 因此可以利用动态规划求解. 动态规划的转移方程:
该式的解读: (m,n)处左上角所有元素之和, 等于少一列,少一行的位置的对应和, 再减去少去一列一行的(因为重复算过一次了), 最后再加该位置(m,n)的.
那么, 如何计算轨迹和检测的重合度呢. 假定有一个轨迹, 将它的位置映射到 M × N M\times N M×N网格坐标(top-left bottom-right)为 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1, y_1), (x_2, y_2) (x1,y1),(x2,y2). 根据上面动态规划转移方程的启示, 我们可以快速算出轨迹的bbox中是否包含了检测:
![[论文阅读笔记17]MAT: Motion-Aware Multi-Object Tracking_第3张图片](http://img.e-com-net.com/image/info8/6d84ac52162843029d306f2fa65a789a.jpg)
因此, 如果上式的结果非0, 则说明有相交的检测, 否则, 这样的配对应该就被舍弃了, 从而简化了cost-matrix:
\space
5. 总体流程
![[论文阅读笔记17]MAT: Motion-Aware Multi-Object Tracking_第5张图片](http://img.e-com-net.com/image/info8/cd72ae7677234ef48d834c5f973f9900.jpg)
综上所述, IML模块负责运动修正, 之后在3DII模块精简detection-track对并进行数据关联, 最后对于inactive的轨迹进行恢复(判断动态寿命)以及轨迹平滑.
6. 评价
这篇文章的工作量可以, 分别对非线性运动相机运动, 目标长时间消失匹配等都做了改进, 但是有以下几个困惑, 愿大家解答:
- 对于运动特征不可靠的轨迹, 缩短了inactive存活寿命, 这是否与长时匹配的初衷相悖?
- IML是如何反向修正轨迹的, 论文并没有说清楚
- 3DII模块, 在计算 I 3 D I_{3D} I3D的时候, 左上角的检测也会使得网格图像右下角存在值, 这会不会和右下角的track关联? 目前的设计我的理解是右下的轨迹不太可能和左上的检测关联.
![[论文阅读笔记17]MAT: Motion-Aware Multi-Object Tracking_第2张图片](http://img.e-com-net.com/image/info8/e266395ae1574f1d9fd1a9e5f55c8db8.jpg)
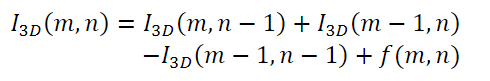

![[论文阅读笔记17]MAT: Motion-Aware Multi-Object Tracking_第4张图片](http://img.e-com-net.com/image/info8/4677b68884bd4080b310aa6f0db1600c.jpg)