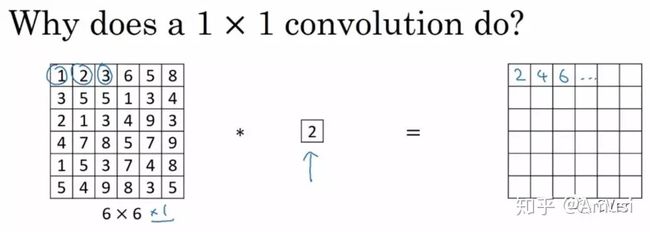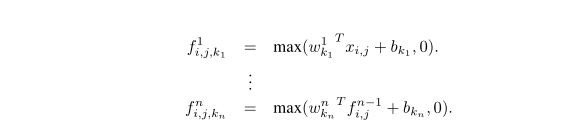卷积神经网络中的1x1卷积核的作用
前言
在介绍卷积神经网络中的1x1卷积之前,首先回顾卷积网络的基本概念[1]。
1. 卷积核(convolutional kernel):可以看作对某个局部的加权求和;它是对应局部感知,它的原理是在观察某个物体时我们既不能观察每个像素也不能一次观察整体,而是先从局部开始认识,这就对应了卷积。卷积核的大小一般有1x1,3x3和5x5的尺寸(一般是奇数x奇数)。
卷积核的个数就对应输出的通道数(channels),这里需要说明的是对于输入的每个通道,输出每个通道上的卷积核是不一样的。比如输入是28x28x192(WxDxK,K代表通道数),然后在3x3的卷积核,卷积通道数为128,那么卷积的参数有3x3x192x128,其中前两个对应的每个卷积里面的参数,后两个对应的卷积总的个数(一般理解为,卷积核的权值共享只在每个单独通道上有效,至于通道与通道间的对应的卷积核是独立不共享的,所以这里是192x128)。
2. 池化(pooling):卷积特征往往对应某个局部的特征。要得到global的特征需要将全局的特征执行一个aggregation(聚合)。池化就是这样一个操作,对于每个卷积通道,将更大尺寸(甚至是global)上的卷积特征进行pooling就可以得到更有全局性的特征。这里的pooling当然就对应了cross region。
与1x1的卷积相对应,而1x1卷积可以看作一个cross channel的pooling操作。pooling的另外一个作用就是升维或者降维,后面我们可以看到1x1的卷积也有相似的作用。
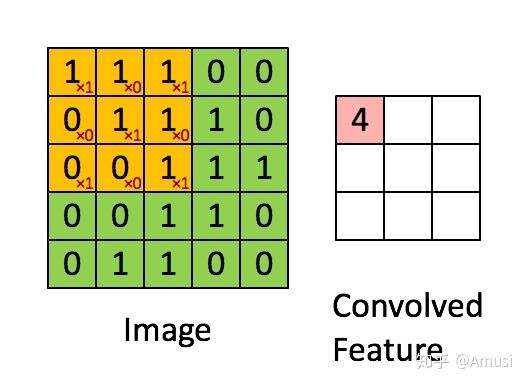
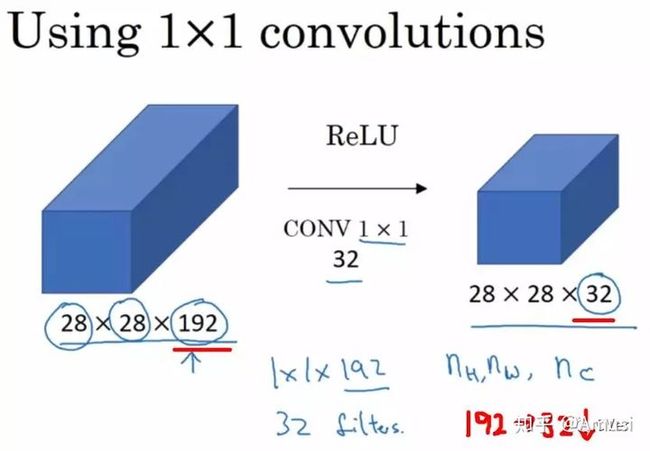
下面从一般卷积过程介绍1x1的卷积,下面图像来表示卷积的过程:
convolution
1x1卷积核
1x1卷积核,又称为网中网(Network in Network)[2]。
这里通过一个例子来直观地介绍1x1卷积。输入6x6x1的矩阵,这里的1x1卷积形式为1x1x1,即为元素2,输出也是6x6x1的矩阵。但输出矩阵中的每个元素值是输入矩阵中每个元素值x2的结果。
上述情况,并没有显示1x1卷积的特殊之处,那是因为上面输入的矩阵channel为1,所以1x1卷积的channel也为1。这时候只能起到升维的作用。这并不是1x1卷积的魅力所在。
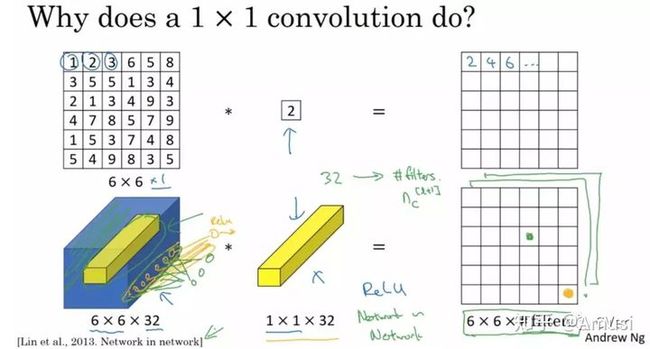
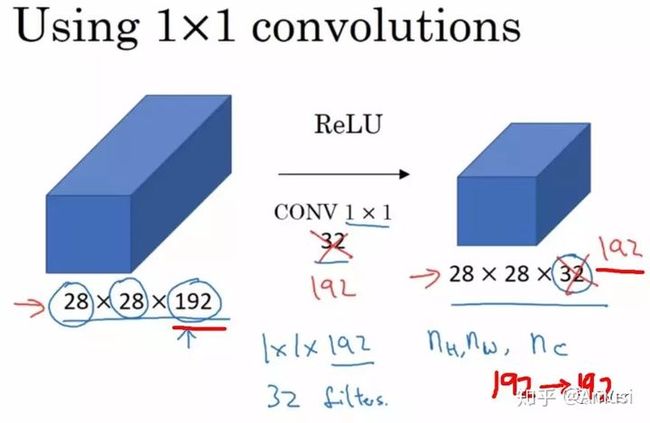
让我们看一下真正work的示例。当输入为6x6x32时,1x1卷积的形式是1x1x32,当只有一个1x1卷积核的时候,此时输出为6x6x1。此时便可以体会到1x1卷积的实质作用:降维。当1x1卷积核的个数小于输入channels数量时,即降维[3]。
注意,下图中第二行左起第二幅图像中的黄色立方体即为1x1x32卷积核,而第二行左起第一幅图像中的黄色立方体即是要与1x1x32卷积核进行叠加运算的区域。
其实1x1卷积,可以看成一种全连接(full connection)。
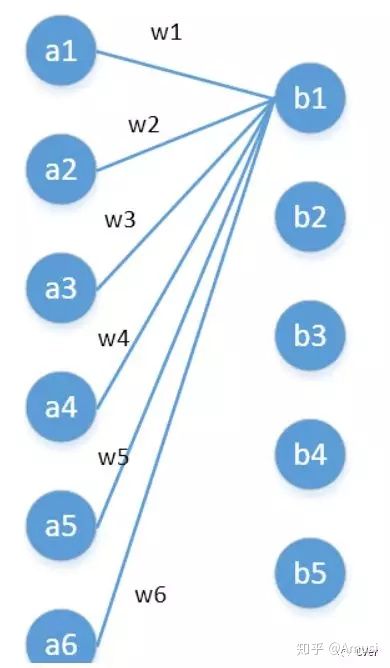
第一层有6个神经元,分别是a1—a6,通过全连接之后变成5个,分别是b1—b5,第一层的六个神经元要和后面五个实现全连接,本图中只画了a1—a6连接到b1的示意,可以看到,在全连接层b1其实是前面6个神经元的加权和,权对应的就是w1—w6,到这里就很清晰了。
第一层的6个神经元其实就相当于输入特征里面那个通道数:6,而第二层的5个神经元相当于1*1卷积之后的新的特征通道数:5。
w1—w6是一个卷积核的权系数,若要计算b2—b5,显然还需要4个同样尺寸的卷积核[4]。
上述列举的全连接例子不是很严谨,因为图像的一层相比于神经元还是有区别的,图像是2D矩阵,而神经元就是一个数字,但是即便是一个2D矩阵(可以看成很多个神经元)的话也还是只需要一个参数(1*1的核),这就是因为参数的权值共享。
注:1x1卷积一般只改变输出通道数(channels),而不改变输出的宽度和高度
1x1卷积核作用
降维/升维
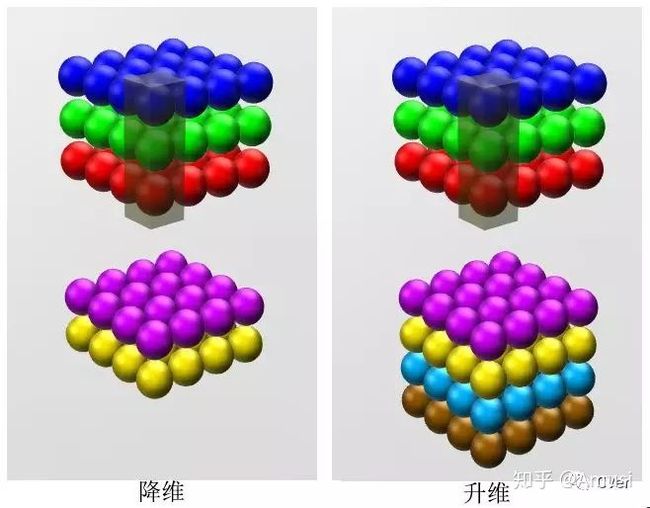
由于 1×1 并不会改变 height 和 width,改变通道的第一个最直观的结果,就是可以将原本的数据量进行增加或者减少。这里看其他文章或者博客中都称之为升维、降维。但我觉得维度并没有改变,改变的只是 height × width × channels 中的 channels 这一个维度的大小而已[5]。
图像来自知乎ID: YJango的回答[6]
增加非线性
1*1卷积核,可以在保持feature map尺度不变的(即不损失分辨率)的前提下大幅增加非线性特性(利用后接的非线性激活函数),把网络做的很deep。
备注:一个filter对应卷积后得到一个feature map,不同的filter(不同的weight和bias),卷积以后得到不同的feature map,提取不同的特征,得到对应的specialized neuron[7]。
跨通道信息交互(channal 的变换)
例子:使用1x1卷积核,实现降维和升维的操作其实就是channel间信息的线性组合变化,3x3,64channels的卷积核后面添加一个1x1,28channels的卷积核,就变成了3x3,28channels的卷积核,原来的64个channels就可以理解为跨通道线性组合变成了28channels,这就是通道间的信息交互[7]。
注意:只是在channel维度上做线性组合,W和H上是共享权值的sliding window
1x1卷积应用
Inception
1. 这一点孙琳钧童鞋讲的很清楚。1×1的卷积层(可能)引起人们的重视是在NIN的结构中,论文中林敏师兄的想法是利用MLP代替传统的线性卷积核,从而提高网络的表达能力。文中同时利用了跨通道pooling的角度解释,认为文中提出的MLP其实等价于在传统卷积核后面接cccp层,从而实现多个feature map的线性组合,实现跨通道的信息整合。而cccp层是等价于1×1卷积的,因此细看NIN的caffe实现,就是在每个传统卷积层后面接了两个cccp层(其实就是接了两个1×1的卷积层)。
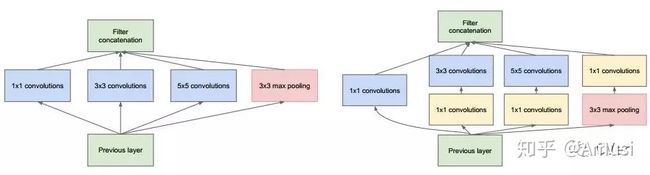
2. 进行降维和升维引起人们重视的(可能)是在GoogLeNet里。对于每一个Inception模块(如下图),原始模块是左图,右图中是加入了1×1卷积进行降维的。虽然左图的卷积核都比较小,但是当输入和输出的通道数很大时,乘起来也会使得卷积核参数变的很大,而右图加入1×1卷积后可以降低输入的通道数,卷积核参数、运算复杂度也就跟着降下来了。
以GoogLeNet的3a模块为例,输入的feature map是28×28×192,3a模块中1×1卷积通道为64,3×3卷积通道为128,5×5卷积通道为32,如果是左图结构,那么卷积核参数为1×1×192×64+3×3×192×128+5×5×192×32,而右图对3×3和5×5卷积层前分别加入了通道数为96和16的1×1卷积层,这样卷积核参数就变成了1×1×192×64+(1×1×192×96+3×3×96×128)+(1×1×192×16+5×5×16×32),参数大约减少到原来的三分之一。
同时在并行pooling层后面加入1×1卷积层后也可以降低输出的feature map数量,左图pooling后feature map是不变的,再加卷积层得到的feature map,会使输出的feature map扩大到416,如果每个模块都这样,网络的输出会越来越大。
而右图在pooling后面加了通道为32的1×1卷积,使得输出的feature map数降到了256。GoogLeNet利用1×1的卷积降维后,得到了更为紧凑的网络结构,虽然总共有22层,但是参数数量却只是8层的AlexNet的十二分之一(当然也有很大一部分原因是去掉了全连接层)[8]。
Inception
ResNet
ResNet同样也利用了1×1卷积,并且是在3×3卷积层的前后都使用了,不仅进行了降维,还进行了升维,参数数量进一步减少,如下图的结构[8]。
其中右图又称为”bottleneck design”,目的一目了然,就是为了降低参数的数目,第一个1x1的卷积把256维channel降到64维,然后在最后通过1x1卷积恢复,整体上用的参数数目:1x1x256x64 + 3x3x64x64 + 1x1x64x256 = 69632,而不使用bottleneck的话就是两个3x3x256的卷积,参数数目: 3x3x256x256x2 = 1179648,差了16.94倍。
对于常规ResNet,可以用于34层或者更少的网络中,对于Bottleneck Design的ResNet通常用于更深的如101这样的网络中,目的是减少计算和参数量(实用目的)[9]。
ResNet
参考
[1] 1*1的卷积核与Inception
[2] 《Network in network》
[3]https://www.coursera.org/lecture/convolutional-neural-networks/networks-in-networks-and-1x1-convolutions-ZTb8x)
[4] 如何理解卷积神经网络中的1*1卷积
[5]【CNN】卷积神经网络中的 1*1 卷积 的作用
[6] https://www.zhihu.com/question/56024942/answer/194997553
[7] 1×1 卷积核的作用?(附实例):
另一篇来自有三AI公众号:【模型解读】network in network中的1*1卷积,你懂了吗
Network In Network 是发表于2014年ICLR的一篇paper。这篇文章采用较少参数就取得了Alexnet的效果,Alexnet参数大小为230M,而Network In Network仅为29M,这篇paper主要两大亮点:
01
提出MLP卷积层
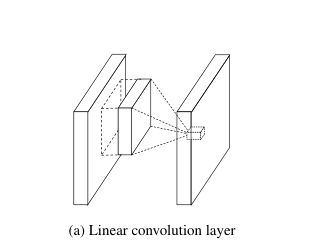
下图是传统卷积结构:
使用relu的一个非线性变换操作为:
i,j表示像素下标,xi,j表示像素值,wk表示卷积参数,k就是下标的索引。
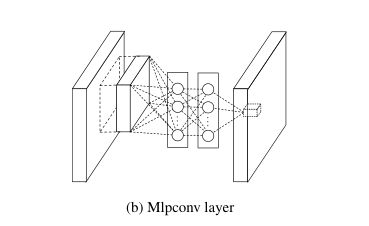
MLP卷积层结构如下图:
mlpconv层的计算公式为:
i,j表示像素下标,xi,j表示像素值,wk,n表示第n层卷积卷积参数。
从以上可以看出,MLP卷积层通过叠加"micro network"网络,提高非线性表达,而其中的"micro network"基本组成单元是1*1卷积网路,说到这,就要解释一下1*1卷积了,该篇论文是首次提出1*1卷积,具有划时代的意义,之后的Googlenet借鉴了1*1卷积,还专门致谢过这篇论文。
1*1卷积的意义:
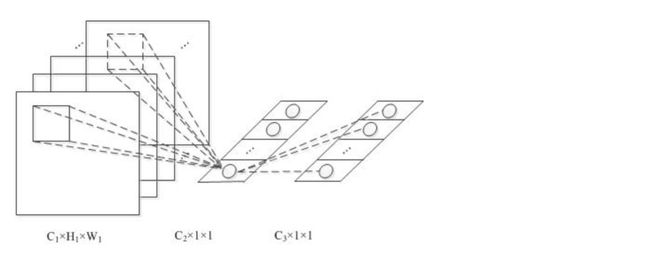
1. 实现了不同通道同一位置的信息融合
如上图,C2融合了C1不同通道同一位置的信息。
2. 可以实现通道数的降维或升维
1*1*n,如果n小于之前通道数,则实现了降维,如果n大于之前通道数,则实现了升维。
02
用全局均值池化代替全连接层
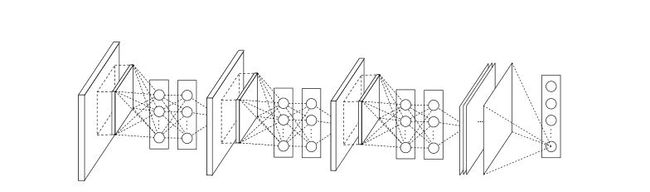
首先让我们看下Network In Network的网络结构,如下图。
上图看出,该网络结构有三个MLP卷积层组成,每个MLP卷积层分别是一个普通卷积,加两个1*1卷积。以1000分类为例,最后一个1*1卷积输出的featuremap大小为6*6*1000。之后每个featuremap采用全局均值池化,输出1000个分类。由于没有全连接的大量参数,使用全局均值池化不需要参数,极大的降低了参数量。
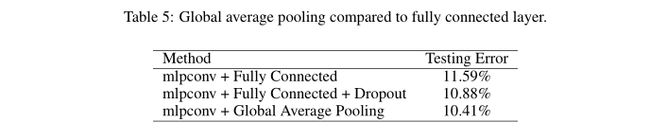
如下图是在CIFAR-10 数据集中 Global average pooling 和 fully connected测试对比图, 从下图可以看出无参数的Global average pooling层 相比较于有参数的全连接层错误率更低。
03
总结
Network In Network通过创新的创建MLP卷积层,提高了网络的非线性表达同时降低了参数量,用全局均值池化代替全连接层,极大的降低了参数量。
[8] 1X1卷积核到底有什么作用呢?ResNet解析 - CSDN博客blog.csdn.net [8] 1X1卷积核到底有什么作用呢?
[8] 1X1卷积核到底有什么作用呢?
[9] ResNet解析 - CSDN博客
扩展知乎话题:卷积神经网络中用1*1 卷积有什么作用或者好处呢?