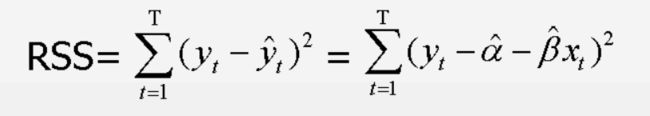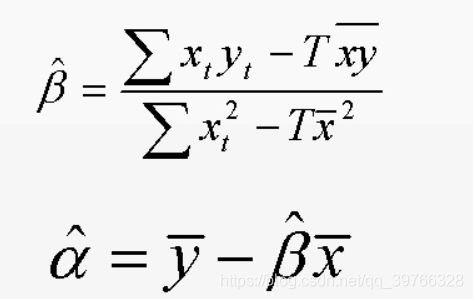二手房房价预测案例 -- 基本概念以及模型应用

1. 分离变量：二分类变量0，1 连续变量（有具体数值含义）

2. 查看样本量&数据描述（print("%d",datall.shape[0])/ dat0.describe(include="all").T ）

3. 二分类变量取频数 画箱线图分析，连续变量与Y变量（价格）同时取对数 相关系数矩阵 画散点图分析

4. 箱形图（Box-plot）  

    又称为盒须图、盒式图或箱线图，是一种用作显示一组数据分散情况资料的统计图。因形状如箱子而得名。它主要用于反映原始数据分布的特征，还可以进行多组数据分布特征的比较。箱线图的绘制方法是：先找出一组数据的上边缘、下边缘、中位数和两个四分位数；然后， 连接两个四分位数画出箱体；再将上边缘和下边缘与箱体相连接，中位数在箱体中间。它能显示出一组数据的最大值、最小值、中位数、及上下四分位数。

    有两种类型的箱图：单式箱图用于分析只有一个变量的数据分布，复式箱图用以分析具有两个或以上变量的数据分布。箱形图提供了一种只用5个点对数据集做简单总结的方式。箱形图很形象的分为中心、延伸以及分布状态的全部范围。箱形图中最重要的是对相关统计点的计算，相关统计点都可以通过百分位计算方法进行实现。

箱形图的分析有以下几个指标：

下四分位数Q1

（1）确定四分位数的位置。Qi所在位置=i（n+1）/4，其中i=1，2，3。n表示序列中包含的项数。

（2）根据位置，计算相应的四分位数。

例中：

Q1所在的位置=（14+1）/4=3.75，

Q1=0.25×第三项+0.75×第四项=0.25×17+0.75×19=18.5；

中位数（第二个四分位数）Q2

中位数，即一组数由小到大排列处于中间位置的数。若序列数为偶数个，该组的中位数为中间两个数的平均数。

例中：

Q2所在的位置=2（14+1）/4=7.5，

Q2=0.5×第七项+0.5×第八项=0.5×25+0.5×28=26.5

上四分位数Q3

计算方法同下四分位数。

例中：

Q3所在的位置=3（14+1）/4=11.25，

Q3=0.75×第十一项+0.25×第十二项=0.75×34+0.25×35=34.25。

上限

上限是非异常范围内的最大值。

首先要知道什么是四分位距如何计算的？

四分位距IQR=Q3-Q1，那么上限=Q3+1.5IQR

下限

下限是非异常范围内的最小值。

下限=Q1-1.5IQR

怎么分析箱形图？

5. 最小二乘线性（OLS）回归模型

基本原则：最优拟合曲线应该使各点到直线的距离的平方和（残差平方和RSS）最小

最小二乘线性（OLS）回归模型

利用最小化一阶条件，对参数求偏导，即可得到α，β的估计量

最小二乘线性（OLS）回归模型

估计量 指的是计算系数的方程，估计值指的是估计出来的系数的数值。

补充最小二乘估计量的性质

（1）最小二乘估计量的基本假设

1、E（μt）=0，即残差具有零均值

2、var（μt）=σ2 ，具有常数方差

3、cov（μi，μj）=0，即残差项之间在统计意义上是相互独立的

4、cov（μt，xt）=0，即残差项与变量无关

5、μt~N（0，σ2），即残差项服从正态分布。

（2）最小二乘法的性质---最优线性无偏性

无偏：意味着就平均意义而言，实际得到的α，β与真实值是一致的

最优：意味着在所有的线性无偏的估计量中，OLS的估计量具有最小方差

（3）估计量的方差、标准差及概率分布

OLS估计量的标准差

最小二乘线性（OLS）回归模型

可以得出：样本量T越大，标准差就越小

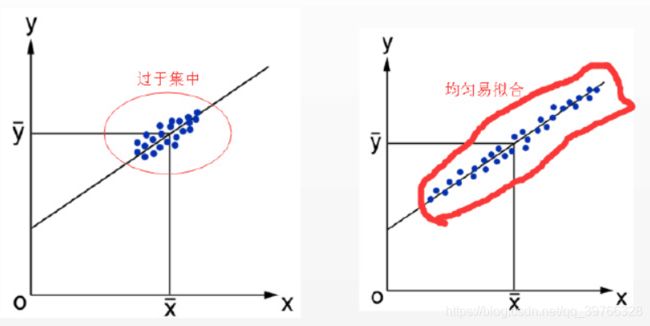
              标准差都取决于残差的方差估计量，残差越小，模型的拟合越好

              标准差还与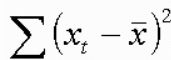有关，其值越小，意味着数据越集中，越难准确估计模型

 

OLS估计量的概率分布

由假设条件5，即μt~N（0，σ2），Yt也服从正态分布

系数估计量也服从正态分布：

值得注意的是：如果残差不服从正态分布，但只要其它假设条件成立，样本量足够大，通常认为系数估计量还是服从正态分布的。

但是，总体回归系数的真实的标准差是得不到的，只能得到样本的标准差。那么用样本的标准差去代替总体的标准差会产生不确定性，标准化的式子服从自由度为T-2的t分布。

正态分布与T分布的关系

t分布的自由度趋于无穷时，t分布就服从正态分布

所以，正态分布可以看做t分布的一个特例。

 

6. 用异方差消除模型误差

   在古典回归模型的假定下，普通最小二乘估计量是线性、无偏、有效估计量，即在所有无偏估量中，最小二乘估计量具有最小方差性——它是有效估计量。如果在其他假定不变的条件下，允许随机扰动项ui存在异方差性，即ui的方差随观测值的变化而变化，这就违背了最小二乘法估计的高斯——马尔柯夫假设，这时如果继续使用最小二乘法对参数进行估计，就会产生以下后果：

1.参数估计量仍然是线性无偏的，但不是有效的；

2.异方差模型中的方差不再具有最小方差性；

3.t检验失去作用；

4.模型的预测作用遭到破坏。

补救措施：

1. 对模型变换，当可以确定异方差 的具体形式时，将模型作适当变换有可能消除或减轻异方差的影响。

2. 加权最小二乘法，对原模型变换的方法与加权二乘法实际上是等价的，可以消除异方差。

3. 买模型的对数变换，运用对数变换能使测定变量值的尺度缩小。它可以将两个数值之间原来10倍的差异缩小到只有2倍的差异。其次，经过对数变换后的线性模型，其残差e表示相对误差，而相对误差往往比绝对误差有较小的差异。