cap2 加州房价预测模型

 获取所需数据集：

import os
import pandas as pd
import tarfile
from six.moves import urllib
DOWNLOAD_ROOT="https://raw.githubusercontent.com/ageron/handson-ml/master/"
HOUSING_PATH="datasets/housing"
HOUSING_URL=DOWNLOAD_ROOT+HOUSING_PATH+"/housing.tgz"

def fetch_housing_data(housing_url=HOUSING_URL,housing_path=HOUSING_PATH): #下载数据集
    if not os.path.isdir(housing_path):
        os.makedirs(housing_path)
    tgz_path=os.path.join(housing_path,"housing.tgz") #拼接路径
    urllib.request.urlretrieve(housing_url,tgz_path) #下载为 housing.tgz压缩文件
    housing_tgz=tarfile.open(tgz_path)
    housing_tgz.extractall(path=housing_path) # 解压
    housing_tgz.close()

def load_housing_data(housing_path=HOUSING_PATH): #加载数据集
    csv_path=os.path.join(housing_path,"housing.csv")
    return pd.read_csv(csv_path) #加载为csv数据类型

 快速查看数据结构（属性、特征信息）：

fetch_housing_data()
housing=load_housing_data()
# housing.head() #查看数据集前5行
# housing.info() #查看数据集的简单描述
# housing["ocean_proximity"].value_counts() #查看类型值属性的值的分类情况
# housing.describe() #显示数值属性摘要，不包括类型值属性
# housing.hist(bins=20,figsize=(20,15)) #各属性的直方图，bins参数设置直方个数

 纯随机抽样，产生测试数据集，占完整数据集的20%：

# from sklearn.model_selection import train_test_split
# train_set,test_set=train_test_split(housing,test_size=0.2,random_state=42) #纯随机抽样，未考虑按照某一属性分层抽样
# print(len(train_set),len(test_set))

 纯随机抽样获取测试集会产生偏差。因为纯随机抽样过程没有考虑不同特征值的分布情况。此例中，要预测的房价平均值与数据集中的收入中位数这一特征值有很大的关系，所以，抽样应符合收入中位数的分布情况，即基于收入中位数的分层抽样。

由于收入中位数是连续的数值属性，需要首先创建一个收入类别的属性，然后把每个类别当成一个层，才能分层抽样。

此例中，大多数收入中位数在2-5之间。数据集中，每一层都要有足够多的实例，所以不能将层数划分的太多。

创建收入类别属性：将收入中位数除以1.5（限制收入类别的数量），然后使用ceil函数取整得到离散类别，最后将所有大于5的类别合并为类别5：

import numpy as np
housing['income_type']=np.ceil(housing['median_income']/1.5)
housing['income_type'].where(housing['income_type']<5,5.0,inplace=True)

 根据收入类别进行分层抽样，使用sklearn的StratifiedShuffleSplit方法：

from sklearn.model_selection import StratifiedShuffleSplit

split=StratifiedShuffleSplit(n_splits=1,test_size=0.2,random_state=42)
for train_index,test_index in split.split(housing,housing['income_type']):
    strat_train_set=housing.loc[train_index]
    strat_test_set=housing.loc[test_index]
housing['income_type'].value_counts()/len(housing) #计算完整数据集中每个类别占的比例

 输出为：

3.0    0.350581
2.0    0.318847
4.0    0.176308
5.0    0.114438
1.0    0.039826
Name: income_type, dtype: float64

 分层抽样结束后，添加的收入中位数类别属性就用不到了，删除此属性：

for set in (strat_train_set,strat_test_set):
    set.drop(['income_type'],axis=1,inplace=True)

 至此，数据预处理完成。

---

 

从数据探索和可视化中获得洞见

创建训练集的副本用来操作，避免损坏训练集。

 

housing=strat_train_set.copy()

 

 将地理数据可视化，设置alpha参数为0.1，可以清楚的看出高密度数据点的位置。

housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.1)

 

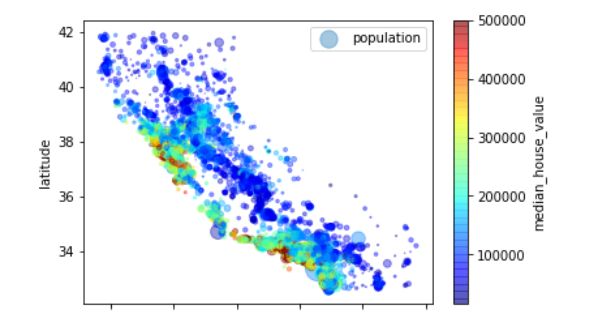
以下代码可以更清楚地可视化信息。每个圆的半径大小代表每个区的人口数量（选项s）；颜色代表价格（选项c）。使用一个名为jet的预定义颜色表（选项cmap）来进行可视化，颜色范围从蓝色（价格低）到红色（价格高）。

housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.4,s=housing['population']/100,
             label="population",c="median_house_value",cmap=plt.get_cmap("jet"),colorbar=True) #alpha表示点的透明度

 

 

---

 

寻找属性之间的相关性

方法1：使用corr()方法计算出每对属性之间的标准相关系数（皮尔逊相关系数）：

corr_mat=housing.corr()

 查看每个属性与房屋价格中位数之间的相关性：

corr_mat['median_house_value'].sort_values(ascending=False)

 输出：

median_house_value    1.000000
median_income         0.687160
total_rooms           0.135097
housing_median_age    0.114110
households            0.064506
total_bedrooms        0.047689
population           -0.026920
longitude            -0.047432
latitude             -0.142724
Name: median_house_value, dtype: float64

 可以看出，收入中位数与房屋价格中位数相关性最高。

 注意：

1、相关系数只能刻画线性相关性（如果x上升，则y上升/下降），所以它有可能彻底遗漏非线性相关性（例如正弦曲线）；

2、相关性大小和斜率大小完全无关。

方法2：使用pandas的scatter_matrix方法可视化每个数值属性相对于其他数值属性的相关性。

此例中有9个数值属性，会产生9*9=81个相关性图像，我们只关注与房屋价格中位数最相关的那些属性。

 

from pandas.plotting import scatter_matrix
attr=['median_house_value','median_income','total_rooms','housing_median_age']
scatter_matrix(housing[attr],figsize=(12,10),color='green',alpha=0.1) 

  输出：

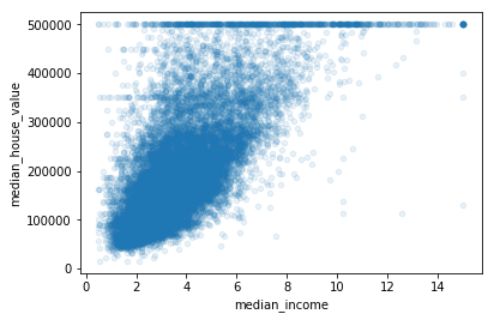
由上图可知，与房屋价格中位数最相关的是收入中位数，放大查看这两个属性的相关性：

housing.plot(kind='scatter',x='median_income',y='median_house_value',alpha=0.1)

 输出：

图中有50万美元、45万美元、35万美元三条直线，这些数据可能会影响算法学习效果，应该删除。

---

 试验不同属性的组合

 在准备给机器学习算法输入数据之前，应该尝试创建各种属性的组合，观察新的属性与目标值之间的相关性。

#添加新的组合属性
housing['rooms_per_household']=housing['total_rooms']/housing['households']
housing['bedrooms_per_room']=housing['total_bedrooms']/housing['total_rooms']
housing['population_per_household']=housing['population']/housing['households']
corr_matrix=housing.corr()
corr_matrix['median_house_value'].sort_values(ascending=False)

 输出：

median_house_value          1.000000
median_income               0.687160
rooms_per_household         0.146285
total_rooms                 0.135097
housing_median_age          0.114110
households                  0.064506
total_bedrooms              0.047689
population_per_household   -0.021985
population                 -0.026920
longitude                  -0.047432
latitude                   -0.142724
bedrooms_per_room          -0.259984
Name: median_house_value, dtype: float64

 表明新属性bedrooms_per_room比原始属性total_bedrooms和total_rooms更有价值。

---

机器学习算法的数据准备

分离训练集上的特征值和标签值：

housing=strat_train_set.drop("median_house_value",axis=1) #分离属性和标签 drop会创建一个副本，不会影响strat_train_set
housing_labels=strat_train_set["median_house_value"].copy()

 数据清理：处理缺失值

方法1：放弃缺失数据的实例

方法2 ：放弃缺失数据的属性

方法3 ：填充中位数值

# housing.dropna(subset=["total_bedrooms"])#方法1，放弃缺失数据的实例
# housing.drop("total_bedrooms",axis=1)#方法2 放弃确实数据的属性
median=housing["total_bedrooms"].median()#方法3 填充中位数值
housing["total_bedrooms"].fillna(median)

 使用sklearn的imputer处理缺失值：首先创建imputer实例，指定要用属性的中位数值替换该属性的缺失值

from sklearn.preprocessing import Imputer
imputer=Imputer(strategy="median")

 由于中位数只能在数值属性上计算，所以先创建一个没有文本属性值的数据集副本：

housing_num=housing.drop("ocean_proximity",axis=1)

 使用fit()方法将imputer实例适配到训练集：

 

imputer.fit(housing_num) #这里imputer只计算了每个属性的中位数，并将结果存储在其实例变量statistics_中。
# imputer.statistics_
# housing_num.median().values #以上两种方法输出的中位数值相同

 

 这里imputer应用于所有属性。虽然只有total_bedrooms属性存在缺失值，但是无法确定以后的新数据是完整的，为了稳妥起见，应用于所有属性。

然后，使用这个实例化的imputer将缺失值替换为中位数值完成训练集的转换：

X=imputer.transform(housing_num) #返回的是Numpy数组
#转换成pandas的DataFrame
housing_trans=pd.DataFrame(X,columns=housing_num.columns)

 注：sklearn的设计原则：1、实例化转换器；2、将转换器fit（适配）到具体的数据集；3、实行transform方法完成转换

 

---

处理文本和分类属性

之前排除了分类属性ocean_proximity，因为它是一个文本属性，我们无法计算它的中位数值。

将文本属性转换为数值属性：sklearn转换器LabelEncoder：

#将文本类别转换为整数类别
from sklearn.preprocessing import LabelEncoder #将文本属性转换为可以计算的数值属性
#使用LabelEncoder转换器来转换文本特征列的方式是错误的，该转换器只能用来转换标签（正如其名）
#在这里使用LabelEncoder没有出错的原因是该数据只有一列文本特征值，在有多个文本特征列的时候就会出错。应使用factorize()方法来进行操作
encoder=LabelEncoder()#实例化LabelEncoder
housing_cate=housing["ocean_proximity"]
housing_cate_encoded=encoder.fit_transform(housing_cate) #housing_cate_encoded是转换后的属性值，是个Numpy一维数组
# housing_cate_encoded
# print(encoder.classes_) #使用classes_属性查看此编码器已学习的映射（文本值映射到数值）

 这种属性值的转换存在一个问题：系统会认为数值间的差代表了文本间的距离，然而并非如此。为了避免由此带来的误差，可以采用独热编码的方式：

#将整数类别转换为独热向量
from sklearn.preprocessing import OneHotEncoder
encoder=OneHotEncoder()
housing_cate_1hot=encoder.fit_transform(housing_cate_encoded.reshape(-1,1)) #reshape(-1,1)表示转换为n行1列的二维数组，n由系统自己推断得出
#fit_transform需要一个二维数组，housing_cate_encoded是一维数组，需要重塑为二维数组
#housing_cate_1hot是一个稀疏矩阵，不是Numpy数组。稀疏矩阵仅存储非零元素的位置，而且可以像使用一个普通二位数组一样使用它。可以使用toarray方法将其转换为二维数组
housing_cate_1hot.toarray()

 输出：

array([[1., 0., 0., 0., 0.],
       [1., 0., 0., 0., 0.],
       [0., 0., 0., 0., 1.],
       ...,
       [0., 1., 0., 0., 0.],
       [1., 0., 0., 0., 0.],
       [0., 0., 0., 1., 0.]])

 可以使用LabelBinarizer一次性完成两个转换，将属性的文本值转换为整数类别再转换为独热向量：

from sklearn.preprocessing import LabelBinarizer
#该类也应用于标签列的转换。正确做法是使用sklearn即将提供的CategoricalEncoder类,下面自定义了这个类。
encoder=LabelBinarizer()
housing_cate_1hot=encoder.fit_transform(housing_cate) 
#housing_cate是属性的文本值，LabelBinarizer默认返回的就是Numpy数组。可以通过设置sparse_output=True得到稀疏矩阵

 

---

自定义转换器：保持与sklearn有一样的接口（fit,transform,fit_transform）

#自定义转换器,添加新的属性
from sklearn.base import BaseEstimator,TransformerMixin
rooms_ix, bedrooms_ix, population_ix, household_ix = 3, 4, 5, 6
class CombinedAttributesAdder(BaseEstimator,TransformerMixin):
    def __init__(self,add_bedrooms_per_room=True):
        self.add_bedrooms_per_room=add_bedrooms_per_room
    def fit(self,X,y=None):
        return self
    def transform(self,X,y=None):
        rooms_per_household=X[:,rooms_ix]/X[:,household_ix]
        population_per_household=X[:,population_ix]/X[:,household_ix]
        if self.add_bedrooms_per_room:
            bedrooms_per_room=X[:,bedrooms_ix]/X[:,rooms_ix]
            return np.c_[X,rooms_per_household,population_per_household,bedrooms_per_room]
        else:
            return np.c_[X,rooms_per_household,population_per_household]
attr_adder=CombinedAttributesAdder(add_bedrooms_per_room=True)
housing_extra_attribs=attr_adder.transform(housing.values)
# housing.head()
# pd.DataFrame(housing_extra_attribs,columns=housing.columns)#报错，housing.columns只有9列，新得到的housing_extra_attribs有12列
# pd.DataFrame(housing_extra_attribs,columns=['longitude', 'latitude', 'housing_median_age', 'total_rooms',
#        'total_bedrooms', 'population', 'households', 'median_income',
#        'ocean_proximity','rooms_per_household','population_per_household','bedrooms_per_room']).head()

 

---

特征缩放：最小最大缩放（MinMaxScaler）和标准化缩放（StandardScaler）。

标准化缩放：减去平均值然后除以方差。受异常值影响小。

转换流水线

数据转换大多需要正确的执行顺序，sklearn提供了Pipeline来支持这样的转换。

#转换流水线 sklearn.pipeline
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

num_pipeline=Pipeline([('imputer',Imputer(strategy='median')),
                       ('attribs_addr',CombinedAttributesAdder()),
                       ('std_scaler',StandardScaler()),
                       ])
housing_num_tr=num_pipeline.fit_transform(housing_num)

  Pipeline构造函数会通过一系列名字/估算器的配对来定义步骤的序列。除了最后一个是估算器之外，前面都必须是转换器（也就是说，必须要有fit_transform方法）。

当调用流水线的fit()方法时，会在所有转换器上按照顺序依次调用fit_transform方法，将一个调用的输出作为参数传递给下一个调用方法，直到传递到最终的估算器，则只会调用fit()方法。

流水线的方法与最终的估算器的方法相同。本例中，最后一个估算器是StandardScaler，这是个转换器，因此Pipeline有transform方法可以按照顺序将所有的转换应用到数据中。

#自定义转换器DataFrameSelector
from sklearn.base import BaseEstimator,TransformerMixin
class DataFrameSelector(BaseEstimator,TransformerMixin):
    def __init__(self,attribute_names):
        self.attribute_names=attribute_names
    def fit(self,X,y=None):
        return self
    def transform(self,X):
        return X[self.attribute_names].values

 一个完整的处理数值属性和分类属性的流水线如下：

 

#一个完整的处理数值属性和分类属性的流水线 
from sklearn.pipeline import FeatureUnion
num_attribs=list(housing_num) #返回的是housing_num的属性名称列表
cate_attribs=["ocean_proximity"]
num_pipeline=Pipeline([
    ('selector',DataFrameSelector(num_attribs)),
    ('imputer',Imputer(strategy='median')),
    ('attribs_adder',CombinedAttributesAdder()),
    ('std_scaler',StandardScaler()),
])
cate_pipeline=Pipeline([
    ('selector',DataFrameSelector(cate_attribs)),
    ('label_binarizer',CategoricalEncoder(encoding="onehot-dense"))
    ])
full_pipeline=FeatureUnion(transformer_list=[
    ('num_pipeline',num_pipeline),
    ('cate_pipeline',cate_pipeline)
])
housing_prepared=full_pipeline.fit_transform(housing)
# housing_prepared.shape

 

 输出：

(16512, 16)

 原书中有错误：参考链接

---

选择和训练模型

 模型一：线性回归模型

from sklearn.linear_model import LinearRegression

lin_reg=LinearRegression()
lin_reg.fit(housing_prepared,housing_labels)
some_data=housing.iloc[:5]
some_labels=housing_labels.iloc[:5]
some_data_prepared=full_pipeline.transform(some_data)
print("预测：\t",lin_reg.predict(some_data_prepared))
print(list(some_labels))

 输出为：

[210644.60459286 317768.80697211 210956.43331178  59218.98886849 189747.55849879]

[286600.0, 340600.0, 196900.0, 46300.0, 254500.0]

 预测结果误差较大。

#使用mean_squared_error函数来测量整个训练集上回归模型的均方误差
from sklearn.metrics import mean_squared_error
housing_preditions=lin_reg.predict(housing_prepared)
lin_mse=mean_squared_error(housing_labels,housing_preditions)
lin_rmse=np.sqrt(lin_mse)
lin_rmse
#误差大概68628，太大，表明模型对训练数据的拟合不足。拟合不足的原因：特征无法提供足够的信息；模型本身不够强大

 输出：

68628.19819848923

 模型二：决策树回归模型

#使用决策树回归模型
from sklearn.tree import DecisionTreeRegressor
tree_reg=DecisionTreeRegressor()
tree_reg.fit(housing_prepared,housing_labels)
#模型已经训练好了，用训练集来评估
housing_predictions=tree_reg.predict(housing_prepared)
tree_mse=mean_squared_error(housing_labels,housing_predictions)
tree_rmse=np.sqrt(tree_mse)
# tree_rmse
#模型的均方误差为0，说明很可能过拟合了

 

---

 

使用交叉验证来更好地进行评估：sklearn的交叉验证功能。

K-折交叉验证：将训练集随机分割成10个不同的子集，每个子集称为一个折叠（fold），然后对决策树模型进行10次训练和评估——每次选择一个折叠进行评估，使用另外9个折叠进行训练。产生的结果是一个包含十次评估分数的数组：

#拿出训练集中的一部分数据用来训练，另一部分用来模型的验证，不是测试集，测试集到最后才能用
#使用交叉验证来更好的评估模型
from sklearn.model_selection import cross_val_score
tree_scores=cross_val_score(tree_reg,housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=10)
tree_rmse_scores=np.sqrt(-tree_scores)

 

def display_scores(scores):
    print("scores:",scores)
    print("均值:",scores.mean())
    print("标准方差：",scores.std())
display_scores(tree_rmse_scores)

 输出：

scores: [68639.12147258 68393.93177789 70347.93898187 69868.17099302 70168.49479261 74439.55860023 70409.44377384 71004.05539331 77484.5192513  69591.386193  ]
均值: 71034.66212296358
标准方差： 2663.896863594895

 该决策树得出的评分为71000±2663.

查看线性回归模型的评分：

lin_scores=cross_val_score(lin_reg,housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=10)
lin_rmse_scores=np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)
#线性回归模型误差小于决策树，说明决策树过拟合了

 输出：

scores: [66782.73843989 66960.118071   70347.95244419 74739.57052552 68031.13388938 71193.84183426 64969.63056405 68281.61137997 71552.91566558 67665.10082067]
均值: 69052.46136345083
标准方差： 2731.6740017983425

 模型三：随机森林回归模型：对特征的随机子集进行许多个决策树的训练，然后对其预测取平均值。

 

#随机森林回归模型：通过对特征的随机子集进行许多个决策树的训练，然后对其预测取平均值。在多个模型的基础上建模，称为集成学习。
from sklearn.ensemble import RandomForestRegressor
forest_reg=RandomForestRegressor()
forest_reg.fit(housing_prepared,housing_labels)
forest_scores=cross_val_score(forest_reg,housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=5)
forest_rmse_scores=np.sqrt(-forest_scores)

 查看误差：

display_scores(forest_rmse_scores)

 输出：

scores: [51734.85224002 53859.50826802 54931.90982477 50658.10686427
 54182.19457144]
均值: 53073.31435370191
标准方差： 1607.9055556878998

 误差比前两个模型小很多。但是，训练集上的分数远低于验证集，这意味着该模型仍然过拟合。

---

微调模型：网格搜索

 

#网格搜索 寻找最优参数组合
from sklearn.model_selection import GridSearchCV
param_grid=[
    {"n_estimators":[3,10,30],'max_features':[2,4,6,8]},
    {'bootstrap':[False],'n_estimators':[3,10],'max_features':[2,3,4]}
]
forest_reg=RandomForestRegressor()
grid_search=GridSearchCV(forest_reg,param_grid,cv=5,scoring='neg_mean_squared_error')
grid_search.fit(housing_prepared,housing_labels)

 模型适配完毕，查看最优参数组合：

grid_search.best_params_

 输出：

{'max_features': 8, 'n_estimators': 30}

 获得最好的估算器：

grid_search.best_estimator_

 输出：

RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
                      max_features=8, max_leaf_nodes=None,
                      min_impurity_decrease=0.0, min_impurity_split=None,
                      min_samples_leaf=1, min_samples_split=2,
                      min_weight_fraction_leaf=0.0, n_estimators=30,
                      n_jobs=None, oob_score=False, random_state=None,
                      verbose=0, warm_start=False)

 GridSearchCV一旦通过交叉验证找到了最好的估算器，它将在整个训练集上重新训练。

评估分数：

cvres=grid_search.cv_results_
for mean_score,params in zip(cvres['mean_test_score'],cvres['params']):
    print(np.sqrt(-mean_score),params)

 输出：

64251.94359079724 {'n_estimators': 3, 'max_features': 2}
55246.84266820805 {'n_estimators': 10, 'max_features': 2}
52997.22536220621 {'n_estimators': 30, 'max_features': 2}
59934.06758448799 {'n_estimators': 3, 'max_features': 4}
53171.412586850485 {'n_estimators': 10, 'max_features': 4}
50707.81355194968 {'n_estimators': 30, 'max_features': 4}
58810.88120203619 {'n_estimators': 3, 'max_features': 6}
52224.71183878166 {'n_estimators': 10, 'max_features': 6}
49877.808283830265 {'n_estimators': 30, 'max_features': 6}
58115.427027082165 {'n_estimators': 3, 'max_features': 8}
52403.98104803142 {'n_estimators': 10, 'max_features': 8}
49792.78396154135 {'n_estimators': 30, 'max_features': 8}
63328.03315591807 {'max_features': 2, 'n_estimators': 3, 'bootstrap': False}
54702.422895264855 {'max_features': 2, 'n_estimators': 10, 'bootstrap': False}
59419.64831075833 {'max_features': 3, 'n_estimators': 3, 'bootstrap': False}
52905.06196990888 {'max_features': 3, 'n_estimators': 10, 'bootstrap': False}
58735.75624311694 {'max_features': 4, 'n_estimators': 3, 'bootstrap': False}
52337.45490553392 {'max_features': 4, 'n_estimators': 10, 'bootstrap': False}

 最好的估算器是：49792.78396154135 {'n_estimators': 30, 'max_features': 8}。效果比随机森林回归模型（53073）好一些。

---

 分析最佳模型极其误差

在进行准确预估时，随机森林回归模型可以指出每个属性的相对重要程度：

 

feature_importances=grid_search.best_estimator_.feature_importances_
# feature_importances
extra_attribs=['rooms_per_household','population_per_household','bedrooms_per_room']
cate_one_hot_attribs=list(encoder.classes_)
attributes=num_attribs+extra_attribs+cate_one_hot_attribs
# print(cate_one_hot_attribs) #['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN']
# print(attributes)
sorted(zip(feature_importances,attributes),reverse=True)

 输出：

[(0.3480653498042381, 'median_income'),
 (0.15894305983142457, 'INLAND'),
 (0.11635023955219795, 'population_per_household'),
 (0.08957448679100119, 'bedrooms_per_room'),
 (0.06447386079398161, 'longitude'),
 (0.06057574679696584, 'latitude'),
 (0.048903786133097385, 'rooms_per_household'),
 (0.04467593231348087, 'housing_median_age'),
 (0.015739859854289447, 'population'),
 (0.01523307512931314, 'total_bedrooms'),
 (0.01485221274387034, 'total_rooms'),
 (0.013451965675787643, 'households'),
 (0.004103803666271844, '<1H OCEAN'),
 (0.0032723332919900815, 'NEAR OCEAN'),
 (0.0017184589373356314, 'NEAR BAY'),
 (6.58286847544412e-05, 'ISLAND')]

 本例中ocean_proximity属性只有INLAND类别是有用的，其他四个类别对预测的贡献很小。

---

 通过测试集评估系统

#使用测试集评估系统
final_models=grid_search.best_estimator_
x_test=strat_test_set.drop('median_house_value',axis=1)
y_test=strat_test_set['median_house_value'].copy()
x_test_prepared=full_pipeline.transform(x_test)
final_predictions=final_models.predict(x_test_prepared)
final_mse=mean_squared_error(y_test,final_predictions)
final_rmse=np.sqrt(final_mse)
final_rmse

 输出：

48029.20843002119

 系统在测试集上表现良好。

 

转载于:https://www.cnblogs.com/zhhy236400/p/11111180.html