leetcode笔记

输入处理

详细可以看这个网址：https://ac.nowcoder.com/acm/contest/5652

输入如下：
a,c,bb
f,dddd
nowcoder
输出如下：
a,bb,c
dddd,f
nowcoder

#include 
#include 
#include 
#include 
using namespace std;
int main()
{
    string s;
    while (getline(cin,s))
    {
        stringstream ss(s);   //赋值给它
        string ans;
        vector vec;
        while (getline(ss,ans,','))   //注意这个语法
        {
            vec.emplace_back(ans);    
        }
        sort(vec.begin(),vec.end());
        for (int i = 0;i


自定义排序
大根堆的自定义排序
/*自定义一个结构体，按其中一个元素排序*/
#include 
#include 
using namespace std;

typedef struct node {
	int x;
	int y;
	struct node(int a,int b) :x(a), y(b){}
}Node;

struct cmp {
	bool operator ()(Node &a,Node &b) {
		return a.xb.y;
	}
};

int main()
{
	priority_queue, cmp> myheal;
	int n;
	cin >> n;
	for (int i = 0;i> a >> b;
		myheal.push(Node(a,b));
	}
	cout << "输出：" << endl;
	
	while (!myheal.empty())
	{
		cout << myheal.top().x << ' ' << myheal.top().y << endl;
		myheal.pop();
	}
	return 0;
}

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XAjaH5TV-1631787002261)(C:\Users\1\AppData\Local\Temp\WeChat Files\b8db3467810c3f55cd47ab689177426.png)]
451. 根据字符出现频率排序
给定一个字符串，请将字符串里的字符按照出现的频率降序排列。
输入:
"tree"

输出:
"eert"

解释:
'e'出现两次，'r'和't'都只出现一次。
因此'e'必须出现在'r'和't'之前。此外，"eetr"也是一个有效的答案。

struct node{
    char ch;
    int nums;
    node(char a,int b):ch(a),nums(b){}
};
struct cmp{
    bool operator ()(node &a,node&b)
    {
        return a.nums hstable;
        for (int i = 0;isecond++;
            }
        }
        priority_queue,cmp> b_heal;
        for(auto i:hstable)
        {
            b_heal.emplace(node(i.first,i.second));
        }
        string ans;
        while(!b_heal.empty())
        {
            for(int i = b_heal.top().nums;i>0;i--)
            {
                ans.push_back(b_heal.top().ch);
            }
            b_heal.pop();
        }
        return ans;
    }
};

vector的自定义排序
#include 
#include 
#include 

using namespace std;

struct node {
	int x;
	int y;
	node(int a, int b) :x(a), y(b) {}
};

bool cmp(node &a, node &b) { return a.x > b.x || (a.x == b.y) && a.y > b.y; }
int main()
{
	int n;
	cin >> n;
	vector vec;
	int a, b;
	for (int i = 0;i> a >> b;
		vec.emplace_back(node(a,b));
	}
	//sort(vec.begin(), vec.end(), [=](node &a, node &b)->bool {return a.x > b.x || (a.x == b.y) && a.y > b.y; });
	sort(vec.begin(), vec.end(), cmp);
	cout << "输出：" << endl;
	for (int i = 0;i< vec.size();i++)
	{
		cout << vec[i].x << ' ' << vec[i].y << endl;
	}

	return 0;
}

map,set存放 类或结构体
map,set 底层是有序的所以要存放结构体、类都需要重载操作符，确定以结构体或者类中的哪个参数排序才可以存放结构体、类了。
#include 
#include 

using namespace std;

struct node {
	int x;
	int y;
	node(int a, int b) :x(a), y(b) {}
	bool operator < (const node& a)const   //需要进行操作符重载   表明待会是这个节点以x为key
	{
		return x < a.x;
	}
};

int main()
{
	map mymap;
	int a, b, w;
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a >> b >> w;
		mymap.emplace(node(a,b),w);
	}
	cout << "find:" << endl;
	int g, h;
	cin >> g >> h;
	if (mymap.find(node(g, h)) != mymap.end())
	{
		cout << "true" << endl;
		cout << "w:" << mymap.find(node(g, h))->second << endl;
	}
	else
		cout << "false" << endl;
	cout << "输出map:" << endl;
	for (auto i = mymap.begin();i!=mymap.end();i++)
	{
		cout << i->first.x << ' ' << i->first.y << ' ' << i->second << endl;
	}
	return 0;
}

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wTplEBtH-1631787002265)(C:\Users\1\AppData\Local\Temp\WeChat Files\476680d3a1bcd968d9f432461492a96.png)]
981. 基于时间的键值存储
创建一个基于时间的键值存储类 TimeMap，它支持下面两个操作：

1. set(string key, string value, int timestamp)

    存储键 key、值 value，以及给定的时间戳 timestamp。

2. get(string key, int timestamp)

    返回先前调用 set(key, value, timestamp_prev) 所存储的值，其中 timestamp_prev <= timestamp。
    如果有多个这样的值，则返回对应最大的  timestamp_prev 的那个值。
    如果没有值，则返回空字符串（""）。
    输入：inputs = ["TimeMap","set","get","get","set","get","get"], inputs = [[],["foo","bar",1],["foo",1],["foo",3],["foo","bar2",4],["foo",4],["foo",5]]
输出：[null,null,"bar","bar",null,"bar2","bar2"]
解释：  
TimeMap kv;   
kv.set("foo", "bar", 1); // 存储键 "foo" 和值 "bar" 以及时间戳 timestamp = 1   
kv.get("foo", 1);  // 输出 "bar"   
kv.get("foo", 3); // 输出 "bar" 因为在时间戳 3 和时间戳 2 处没有对应 "foo" 的值，所以唯一的值位于时间戳 1 处（即 "bar"）   
kv.set("foo", "bar2", 4);   
kv.get("foo", 4); // 输出 "bar2"   
kv.get("foo", 5); // 输出 "bar2"  

struct node{
    int time;
    string value;
    node(int a,string b):time(a),value(b){}
    bool operator < (const node& a)const    //以time为key值
    {
        return timevalue; 
        }
        return "";                                                   //没找到
    }
private:
    unordered_map> hstable;
};

/**
 * Your TimeMap object will be instantiated and called as such:
 * TimeMap* obj = new TimeMap();
 * obj->set(key,value,timestamp);
 * string param_2 = obj->get(key,timestamp);
 */

哈希表存放 类或结构体
对于int string 可以直接使用，底层模板是支持这两个类的。需要指定用结构体中哪个成员作为key;
需要重载。
#include 
#include 
#include 
using namespace std;

struct node {
	int x;
	int y;
	node(int a,int b) :x(a), y(b) {}
};
bool operator == (const node& a,const node &b)  //需要重载这两个函数
{
	return a.x == b.x && a.y == b.y;
}
struct cmp {
	size_t operator()(const node& a)const {  //size_t改为int也是可以的
		int zhi = a.x;
		return std::hash()(zhi);
	}
};
int main()
{
	unordered_set hs;  //第二个函数是确定根据哪个key进行排序
	int n;
	cin >> n;
	int a, b;
	for (int i = 0;i> a >> b;
		hs.emplace(node(a,b));
	}
	cout << "find输入：" << endl;
	int g, h;
	cin >> g >> h;
	if (hs.find(node(g, h)) != hs.end())
	{
		cout << "ture" << endl;
	}
	else
		cout << "false" << endl;
	//cout << hs.find(node(1, 2))->x << hs.find(node(1 ,2))->y << endl;

	return 0;
}

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-r4fm7NCb-1631787002268)(C:\Users\1\AppData\Local\Temp\WeChat Files\0ed2b94a0d0f08736fe1a7b61f7b95f.png)]
56. 合并区间
class Solution {
public:
    vector> merge(vector>& intervals) {
        vector> ans;
        sort(intervals.begin(),intervals.end(),[=](vector &a,vector &b)->bool{
            return a[0] mid;
        for(int i = 0;i=intervals[i+1][0] && end<=intervals[i+1][1]){
                end = intervals[i+1][1];
            }
            else if(end

剑指 Offer 45. 把数组排成最小的数
class Solution {
public:
    string minNumber(vector& nums) {
        vector mystr;
        for(int i = 0 ;ibool{
            return a+b

剑指 Offer 50. 第一个只出现一次的字符
typedef struct node{
    int index;
    int nums;
    node(int a,int b):index(a),nums(b){}
}Node;
class Solution {
public:

    char firstUniqChar(string s) {
        vector mynode(26,Node(0,0));
        char ans = ' ';
        for(int i = 0;i myvec;
        for(int i =0;ibool{
            return a.index

排序
冒泡排序
选择排序
插入排序
希尔排序
归并排序
堆排序
底层是一个完全二叉树，可以用一个数组来表示一颗完全二叉树
表示规则如下：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rgUZX8Ab-1631787002271)(C:\Users\1\AppData\Local\Temp\WeChat Files\badd172212405b7bdaa33814f4ceae4.png)]
桶排序

快排
快排思想：先在数组中选择一个数字，接下来把数组中的数字分为两部分，比选择的数字小的数字移到数组的左边，比选择的数字大的数字移到数组的右边。
void swap(int &a, int &b)
{
	int temp = a;
	a = b;
	b = temp;
}
//快排
void quicksort(vector& arr,int left, int right)
{
	if (arr.size() <= 1 || left > right)return;  //去除无效数据
	int l = left;
	int r = right;
    //其中arr[left] 就是key
	while (l!=r)
	{
		while (arr[r] >= arr[left] && r > l)r--;
		while (arr[l]<=arr[left] && r>l)l++;
		if (l < r)swap(arr[r],arr[l]);
	}
	swap(arr[l],arr[left]);
	quicksort(arr,left,l-1);
	quicksort(arr,l+1,right);
}

应用：
面试题 17.14. 最小K个数
class Solution {
public:
    vector ans;
    void swap(int *a,int *b)   //交换
    {
        int temp = *a;
        *a = *b;
        *b = temp;
    }
    void qsort(vector& arr,int k,int left,int right)
    {
        if (left>right)return ;     //base case 
        int l = left;
        int r = right;
        int key = left;
        while (l=arr[key]&&lk){
            qsort(arr,k,left,l-1);
        }else{
            qsort(arr,k,l+1,right);
        }   
    }
    vector smallestK(vector& arr, int k) {
        qsort(arr,k,0,arr.size()-1);
        return ans;
    }
};

查找
二分查找
题目特征：有序，或者部分有序
一般二分查找的过程：
1.找到中间的关键字 (选取关键字是很重要的一步)
2.比较查找的关键字与中间关键字的大小关系
3.如果相等就相当于已经找到
4.如果查找的关键字小于中间关键字则在前半部分进行同样的过程（从小到大存储）
5.如果查找的关键字大于中间的关键字则在后半部分进行同样的过程（从小到大存储）
一般二分查找要求：
1.顺序存储
2.元素有序 ，局部有序也是可以的
lower_bound:返回数组中第一个****大于等于该元素的下标，auto aa = lower_bound(array,array+arrayLen,num) ;
upper_bound:返回数组中第一个****大于该元素的下标：auto aa = upper_bound(array,array+arrayLen,num) ;
按从小到大的顺序
返回的是指针，是vector中内置的二分查找法
//vector存放结构体。自定义以哪个为key值
bool cmp (int time,const node& a)
    {
        return time

剑指 Offer 11. 旋转数组的最小数字
class Solution {
public:
    int minArray(vector& numbers) {
        int left = 0,right = numbers.size()-1;
        int mid =(left+right)/2;
        while(leftnumbers[right]){
               left = mid+1;
           }else if(numbers[mid]==numbers[right]){
               right--;
           }
            mid = (left+right)/2;
        }
        return numbers[mid]; 
    }
};
//2021.5.21

上面这道题，numbers[right] 就是就是关键字，numbers[mid]与之相比较，确定4，5步的移动策略
顺序查找
哈希表查找
128. 最长连续序列
给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。
进阶：你可以设计并实现时间复杂度为 O(n) 的解决方案吗？

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

方法一：先排序后判断
class Solution {
public:
    int longestConsecutive(vector& nums) {
        if(nums.size() == 0)return 0;
        sort(nums.begin(),nums.end());
        int ans = 1;
        int temp = 1;
        for (int i = 0;i

方法2：哈希表法
用set储存，有序且方便快速查找
首先，要找到 nums 中有哪些元素能够当做连续序列的左边界。
假设 a 为一个连续序列的左边界，则 a - 1 就不可能存在于数组中。 因为，若 a - 1 存在于 nums 数组中，则 aaa 不可能成为连续序列的左边界。
所以，若一个元素值 a 满足：a - 1 不在 nums 数组中，则该元素值 a 就可以当做连续序列的左边界。
要利用一个可以快速查找的数据结构来存储 nums 数组中的元素，并且遍历（因为 set 在存储时有去重的功能，所以运行时间要比 listlistlist 快的多）。
若 a - 1 存在于 list（set） 中，则 a 不可能是左边界，直接跳过；
class Solution {

    public int longestConsecutive(int[] nums) {

        int n = nums.length;
        if (n == 0) return n;
        //List list = new ArrayList<>();
        HashSet set = new HashSet<>();

        for (int i=0;i list

            if (set.contains(a - 1)) {

                continue;
            } else {

                int len = 0;
                while (set.contains(a++)) { //注意这里的处理  a++

                    len++;
                }
                maxLength = Math.max(len, maxLength);
            }
        }
        return maxLength;
    }
}

二叉排序树查找
对应的数据结构是二叉搜索树
双指针
167.给定一个已按照 升序排列 的整数数组 numbers ，请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ，所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length 。
你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。
eg:输入：numbers = [2,7,11,15], target = 9
 输出：[1,2]
 解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
class Solution {
public:
    vector twoSum(vector& numbers, int target) {
        /*vector ans;
        int zhi = 0;
        for(int i = 0;izhi)break;
            }
        }
        return ans;*///这种时间复杂度（考虑最差情况下）n2
        /*双指针法*/  //这个方法的时间复杂度为on
        vector ans;
        int left = 0,right = numbers.size()-1;
        while(left!=right)
        {
            if((numbers[left]+numbers[right])==target)
            {
                ans.push_back(left+1);
                ans.push_back(right+1);
                return ans;
            }
            if((numbers[left]+numbers[right])>target)right--;
            else if ((numbers[left]+numbers[right])

leetcode 11.15.16都是双指针的题目
11. 盛最多水的容器
class Solution {
public:
    int maxArea(vector& height) {
        int ans=0;
        int left = 0,right = height.size()-1;//定义左右指针
        while(left!=right)
        {
            int sum = min(height[left],height[right])*(right-left);
            ans = sum>ans?sum:ans;
            if(height[left]

综上的两道题，都有目标值，在移动过程中要考虑从如何移动指针，与逼近目标值的策略。通常还要考虑需不需要给数组排序
209. 长度最小的子数组
class Solution {
public:
    int minSubArrayLen(int target, vector& nums) {
        int ans =0;
        int max =10000;
        int left = 0,right = 0;  //定义左右指针
        int sum = nums[left];//定义一个存放总和的数
        while(1)
        {
            if(sum>=target)
            {
                ans = (right-left+1)(nums.size()-1))return ans;
                sum+=nums[right];
            }
        }
        return ans;
    }
};
//2021.3.3双指针   --感觉是用快慢指针来解决
//很经典的一道题，只遍历了一遍数组，所以时间复杂度On。注意怎么移动两根指针是这道题的关键

面试题 16.16. 部分排序
双指针中一道快慢指针，很是经典。
class Solution {
public:
    vector subSort(vector& array) {
        int left = 0 ,right = 0,max = 0;//定义双指针   这里选用快慢指针
        int right_chrid = 0;
        vector ans(2,-1);
        if(array.size()<=2)return ans;
        while((left>=0)&&((right+1)<=(array.size()-1)))
        {
           if(array[right+1]>=array[right])
           {
               left++;
               right++;  //左右指针都自加
           }
           else
           {
               max = array[right];
               right++;
               while(((right+1)<=array.size()-1))
               {
                    if(left!=0&&array[right]=max)//大于max值时就要开始判断了，这个时候就有可能出现答案中的右值，需要将进一步判断
                    {
                        //std::cout<<"max:"<=array[right])right++;
                            if(right==array.size()-1)  //最后一个位置了
                            {
                                right= right_chrid-1;//right--;   //note
                                ans.clear();
                                ans.push_back(left);
                                ans.push_back(right);
                                return ans;
                            }
                            else{//不是最后一个位置的时候就要更新右指针的位置。
                                max = array[right];
                            } 
                        }
                        else
                            break;
                    }
               }
               ans.clear();
               ans.push_back(left);
               ans.push_back(right);
               return ans;
           }
        }
        return ans;
    }
};
//2021.3.3 自我感觉是用双指针实现
//难度左右指针的移动策略  快慢指针
//只遍历了一遍数组，所以时间复杂的为On，空间复杂度上看 O1

时间复杂度和空间复杂度均为最佳。
链表
知识点：1.旋转链表 2.判断链表有无换 3.入环结点
删除链表的倒数第 N 个结点
解法一。
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        /*法一*/
        ListNode* ans  = new ListNode;
        ans = head;
        int num = 0;
        while(head!=nullptr)
        {
            num++;
            head=head->next;
        }
        int m = num-n;
        if(m==0)return ans->next;//指向第一个节点
        ListNode* out = ans;
        for(int i=0;i<(m-1);i++)
        {
            ans = ans->next;
        }
        ans->next = ans->next->next;//修改
        return out;
    }
};
//2021.3.2 暴力解法  法一


//牛客上  2021.7.8
/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head ListNode类 
     * @param n int整型 
     * @return ListNode类
     */
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        
        if(n == 0)return head;
        ListNode* temp = new ListNode(0);
        temp->next = head;
        ListNode* ans = head;
        ListNode* temp2 = temp;
        for (int i = 0;inext;
        }
        if(temp2->next == nullptr)return ans->next;
        while (temp2->next != nullptr)
        {
            temp2 = temp2->next;
            temp = temp->next;
        }
        ListNode *temp3 = temp->next->next;
        temp->next = temp3;
        return ans;
    }
};

上面这个做法是暴力解法，遍历两次链表。所以时间复杂度为On2。进阶做法是只是遍历一次链表，时间复杂度就是On.
61. 旋转链表
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
        if(head == nullptr ||head->next == nullptr || k == 0){
            return head;
        }
        ListNode* left = head;
        ListNode* right = head;    //定义了快慢指针
        int zhi = k;
        int mid = k;
        while(k){      
            if(right->next == nullptr && k!=1){   //这一步用于确定k的值，这是当k值远大于链表长度的情况
                k--;
                zhi = zhi-k;  //得到整个链表的长度
                k = mid%zhi;  //摸运算
                if(k == 0) return head;  //这种情况已经可以说明，后面无需再移动了 ， 直接退出
                right = head;
                //std::cout<next == nullptr && k == 1){
                right = right->next;
                break;
            }
            if(right->next!=nullptr){
                right = right->next;
            }
            k--;
        }
        ListNode* ans = nullptr;
        if(right == nullptr)return head;
        while(right->next!=nullptr){
            left = left->next;     //移动左指针
            right= right->next;      //移动右指针
        }
        ans = left->next;
        right->next = head;
        left->next = nullptr;   
        return ans;
    }
};
//2021.3.27 快慢指针法 = 分治+ 链表操作

分治的思想，每一步都要考虑清楚，把题目中提供的信息尽可能的挖掘出来，比如实例，说明等等。。。
coding的时候，应该把握主方向，不要在一个代码思路上死干
剑指 Offer 35. 复杂链表的复制
用了左程云的那种做法，
/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/
class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(head == nullptr)return nullptr;
        Node* mid = nullptr;
        Node* thenext = nullptr;
        Node* root = head;
        Node* yushi = head;
        while(head != nullptr)  //复制next 插入节点
        {
            mid = head->next;
            thenext = new Node(head->val);
            head->next = thenext;
            thenext->next = mid;
            head = mid;
        }
        Node* out = root->next;
        while(root != nullptr)  //复制random
        {
            if(root->random == nullptr) root->next->random = nullptr;
            else
                root->next->random = root->random->next;
            root = root->next->next;
        }
        //剥离
        Node* ans = out;
        head = yushi;
        while(out->next != nullptr)
        {
            mid = out->next;
            yushi->next = mid;
            yushi = mid;
            out->next = mid->next;
            out = mid->next;
        }
        yushi->next = nullptr;
        return ans;
    }
};
//2021.4.2
//法一
//法二 哈希表法

可以尝试用哈希表法，unordered_map,key是存放原始节点，value是放复制后的节点
1721. 交换链表中的节点
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapNodes(ListNode* head, int k) {
        ListNode* left = head;
        ListNode* right = head;
        int zhi = 1;
        while(zhi != k && right->next != nullptr)
        {
            zhi++;
            right = right->next;
        }
        ListNode* first = right;
        while(right->next != nullptr)
        {
            right = right->next;
            left = left->next;
        }
        ListNode* second = left;
        //交换值
        int mid=0;
        mid = first->val^second->val;
        second->val = mid^second->val;
        first->val = mid^first->val;
        return head;
    }
};
//2021.4.2 快慢指针  找到节点，交换值，返回链表头节点即可

24. 两两交换链表中的节点
双指针+辅助结点（选好一个辅助节点是很重要的）
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(head == nullptr) return nullptr;
        if(head->next == nullptr) return head;   //去除无效数据
        ListNode* yaba = new ListNode();
        yaba->next = head;
        ListNode* left = head;
        ListNode* right = left->next;
        bool flag = false;
        while(left->next!=nullptr)
        {
            left->next = right->next;
            right->next = left;
            yaba->next = right;
            if(!flag){
                flag = true;
                head = right;
            }
            yaba = left;
            left = left->next;
            if(left == nullptr || left->next == nullptr)break;
            right = left->next;
        }
        return head;
    }
};
//2021.4.2

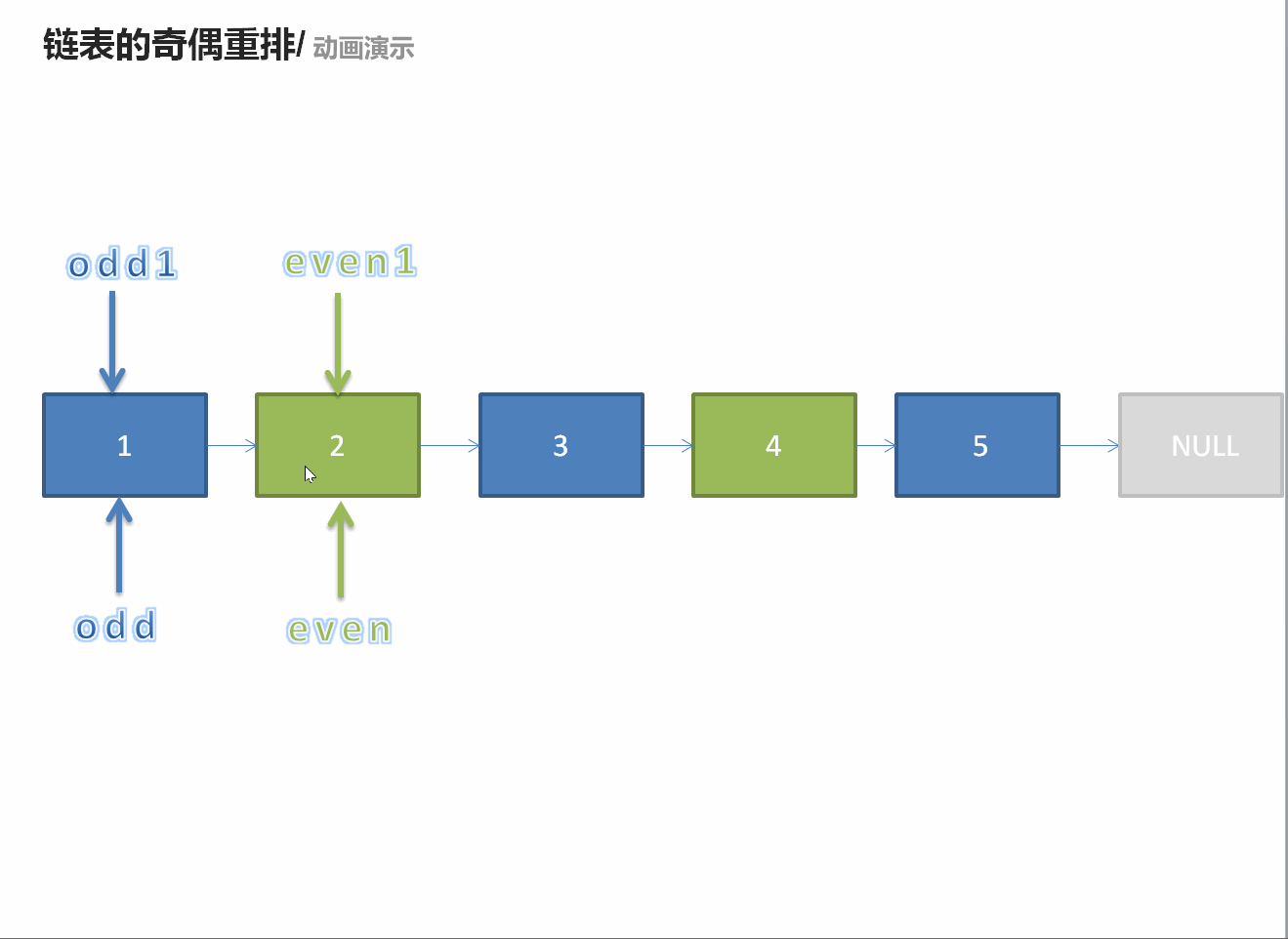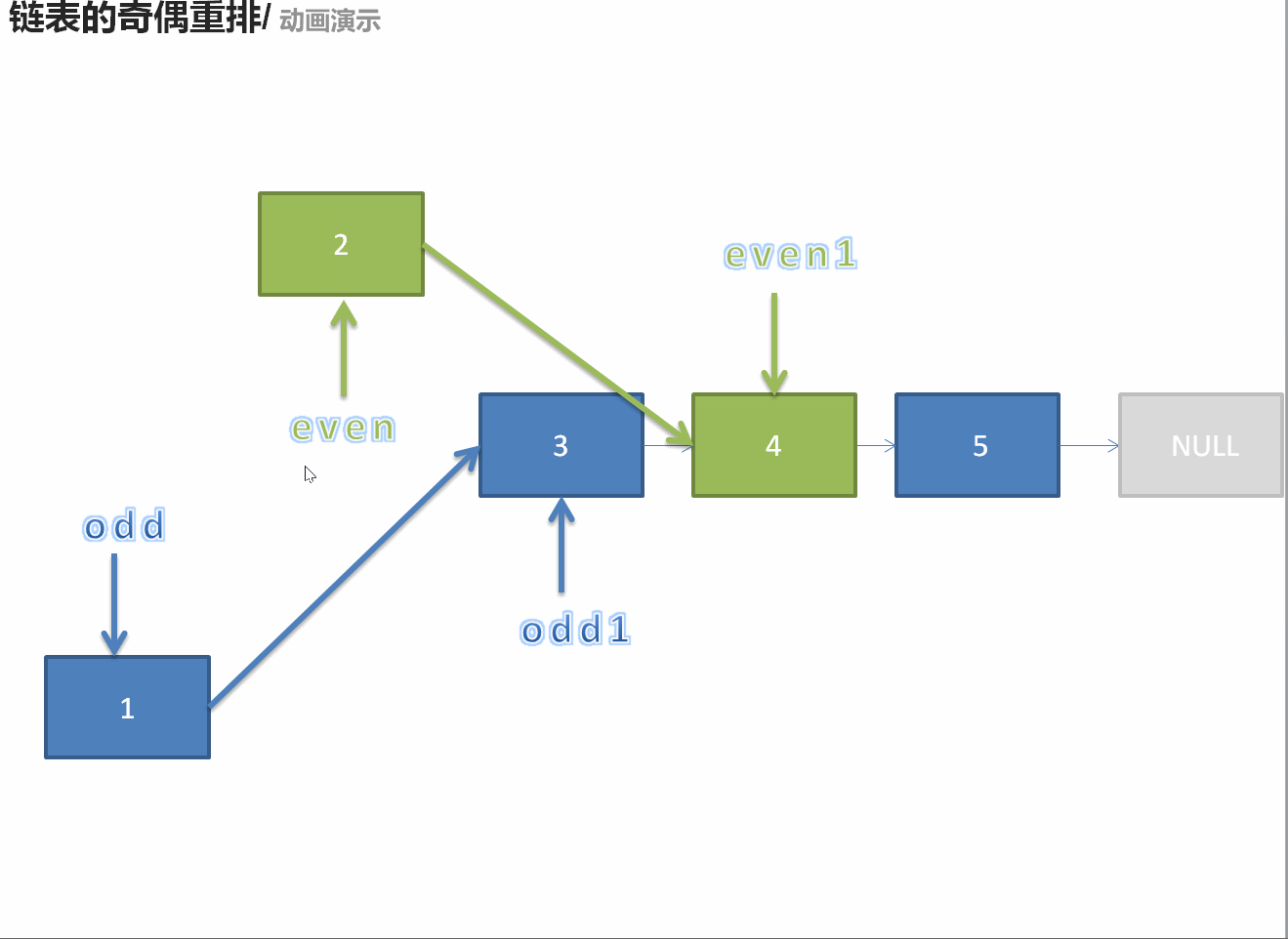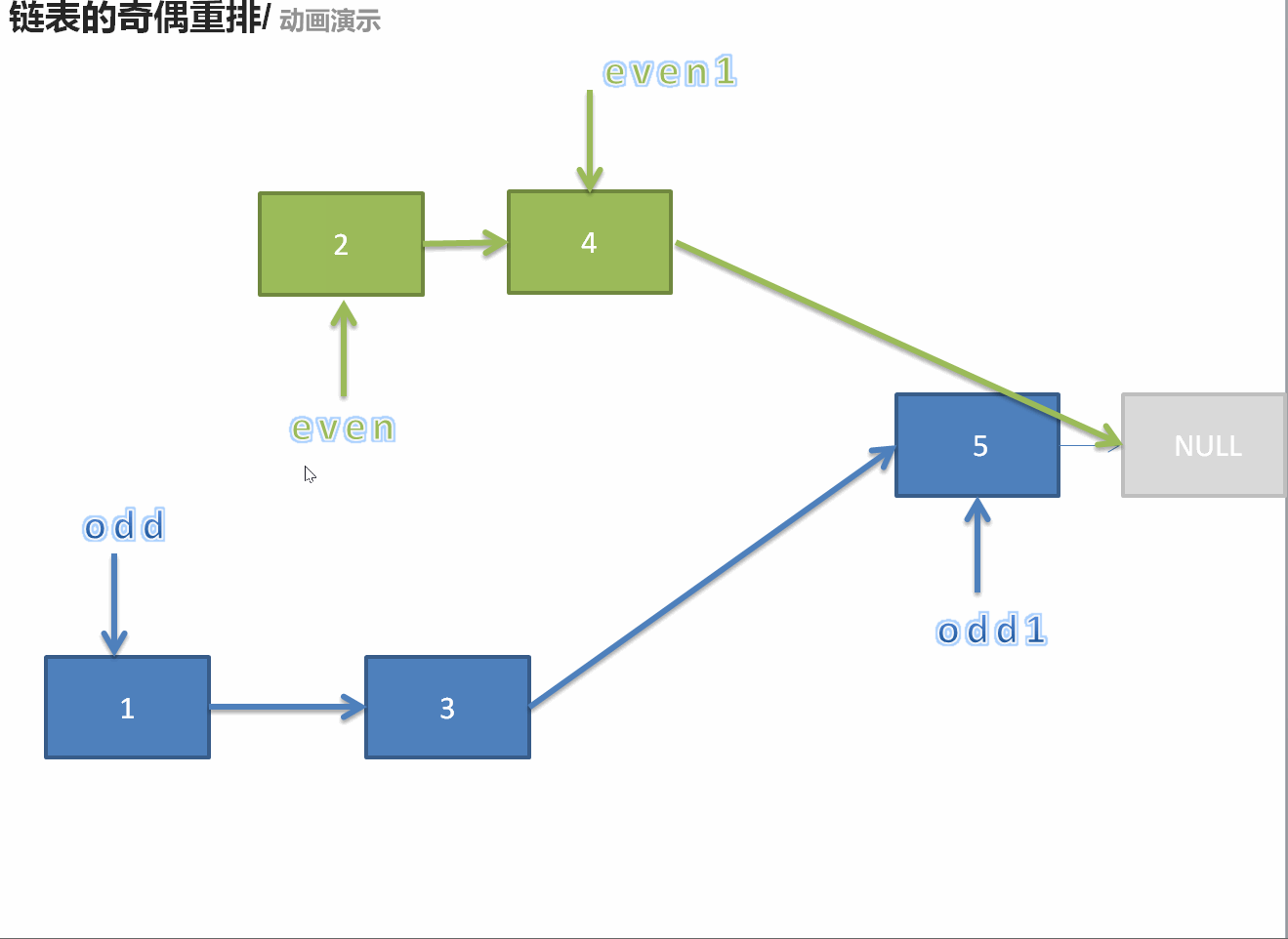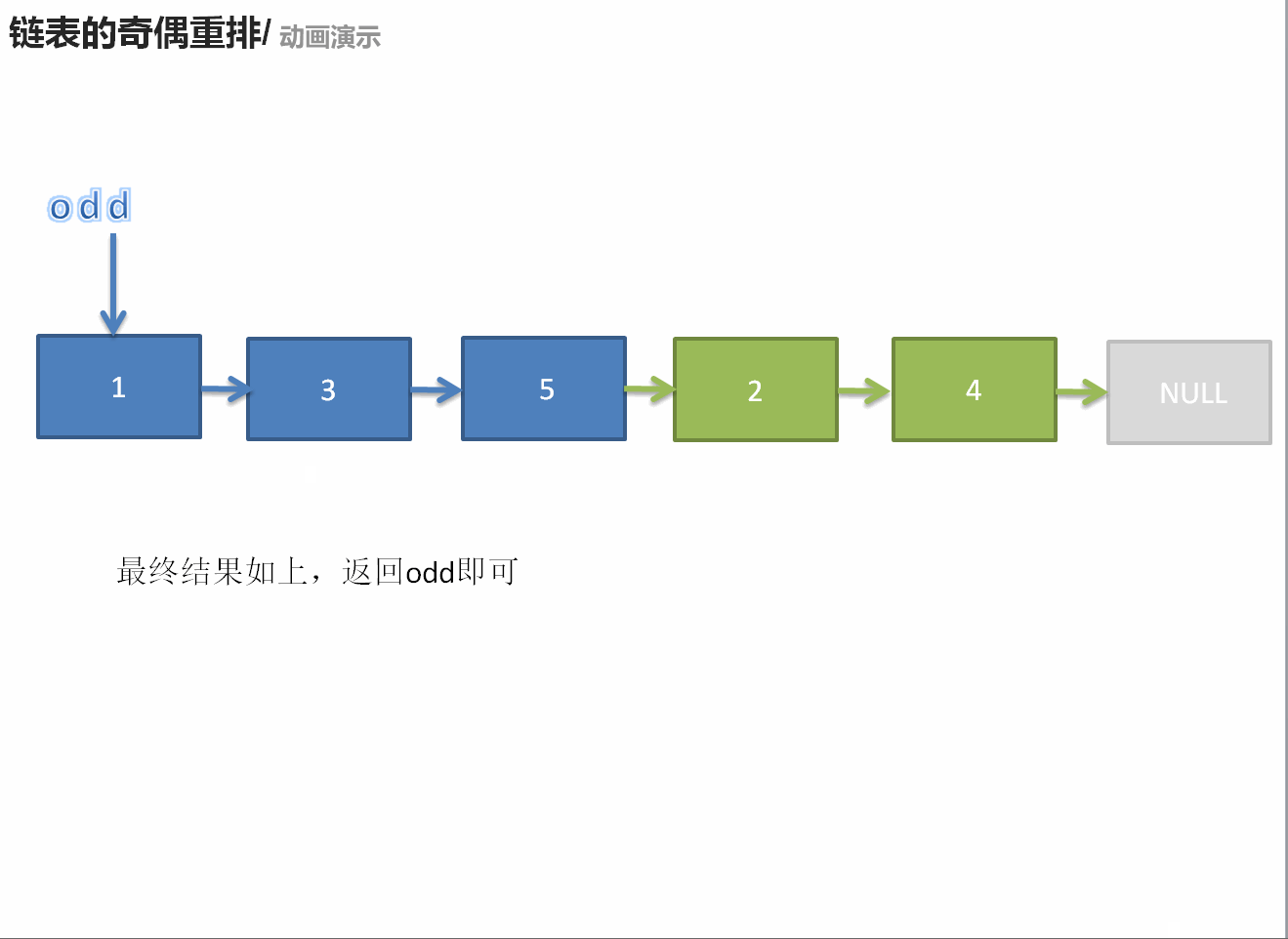
328. 奇偶链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* oddEvenList(ListNode* head) { 
        if(head == nullptr || head->next == nullptr)return head;
        ListNode* odd = head;
        ListNode* ans = odd;
        ListNode* even = head->next;
        ListNode* temp = even;
        while(even != nullptr && even->next != nullptr){
            odd->next = even->next;
            odd = even->next;
            even->next = odd->next;
            even = even->next;
        }
        odd->next = temp;
        return ans;
    }
};

链表中倒数最后k个结点
描述
输入一个链表，输出一个链表，该输出链表包含原链表中从倒数第k个结点至尾节点的全部节点。
如果该链表长度小于k，请返回一个长度为 0 的链表。

输入：

{1,2,3,4,5},1 

返回值：
{5}

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 *	ListNode(int x) : val(x), next(nullptr) {}
 * };
 */
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param pHead ListNode类 
     * @param k int整型 
     * @return ListNode类
     */
    ListNode* FindKthToTail(ListNode* head, int k) {
        // write code here
        ListNode *temp = new ListNode(0);
        temp->next = head;   //辅助节点
        ListNode *cur = temp;
        ListNode *ptr = temp;      //双指针节点
        for (int i = 0;inext == nullptr)return nullptr;
            ptr = ptr->next;
        }
        while (ptr!=nullptr)
        {
            ptr = ptr->next;
            cur = cur->next;
        }
        
        return cur;
    }
};

剑指offer
数组
剑指 Offer 03. 数组中重复的数字f
class Solution {
public:
    int findRepeatNumber(vector& nums) {
         //法一
        /*sort(nums.begin(),nums.end());//排序   Onlogn
        for(int i = 0;i<(nums.size()-1);i++)    //On
        {
            if(nums[i] == nums[i+1])return nums[i];
        }
        return 0;*/  //时间复杂度为On  ， 空间复杂度为On
        
        //法二  哈希表法
       /* unordered_set biao;  //定义了一个哈希表
        for(int i = 0 ;i < nums.size() ; i++)
        {
            if(biao.find(nums[i]) != biao.end())return nums[i];
            else
                biao.insert(nums[i]);
        }
        return 0;*/

        //原地置换法  最佳方案
        int zhi = 0;
        while(zhinums[zhi])return nums[zhi];   //前面已经排序了
                if(nums[zhi] == nums[nums[zhi]])return nums[zhi];  //在交换位置之前做一次判断。
                swap(nums[zhi],nums[nums[zhi]]);   //swap 这个可以直接用
            }
        }
        return 0;

    }
};
//2021.3.11  朴素法
//2021.3.12  哈希表法
//2021.3.12  原地置换法  最佳方案

法三是因为题目中已经有提示，一定要好好审题，这比什么都重要
二叉树
这一部分有一些常规问题如下：
1.前序、中序、后序遍历，输出tree的值
先说一下这几种遍历的概念：
前序：根节点在最前面，接着是左孩子，右孩子
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
//迭代解法
class Solution {
public:
    vector preorderTraversal(TreeNode* root) {
        vector ans;
        stack mystack;
        if (root!=nullptr)mystack.push(root);
        while (!mystack.empty())
        {
            TreeNode* temp = mystack.top();
            mystack.pop();
            ans.emplace_back(temp->val);
            if (temp->right!=nullptr)mystack.push(temp->right);
            if (temp->left!= nullptr)mystack.push(temp->left);
        }
        return ans;
    }
};

中序：左孩子，根节点，右孩子
class Solution {
public:
    vector inorderTraversal(TreeNode* root) {
        vector ans;
        stack mystack;
        while (root!= nullptr||!mystack.empty())
        {
            while (root!=nullptr)
            {
                mystack.push(root);
                root = root->left; //先压入根节点和做结点
            }
            ans.emplace_back(mystack.top()->val);
            root = mystack.top()->right;
            mystack.pop();
        }
        return ans;
    }
};

后序：左孩子，右孩子，根节点
前序结果取反就行
class Solution {
public:
    vector postorderTraversal(TreeNode* root) {
        vector ans;
        stack mystack;
        stack temp_stack;
        if (root != nullptr)mystack.push(root);
        while (!mystack.empty())
        {
            TreeNode* temp = mystack.top();
            mystack.pop();
            temp_stack.push(temp->val);  //前插
            if (temp->left != nullptr)mystack.push(temp->left);
            if (temp->right != nullptr)mystack.push(temp->right);
        }
        while (!temp_stack.empty())
        {
            ans.emplace_back(temp_stack.top());l
            temp_stack.pop();
        }
        return ans;
    }
};

下面提供一个模板代码：
//递归解法
void bianli(TreeNode* root,vector& nums){   //root为一颗树的头节点，nums是要保存数据的数组
        if(root == nullptr){
            return ;   //返回空，意思是结束，返回了
        }
        //1
        bianli(root->left,nums);
        //2
        bianli(root->right,nums);   //中序遍历  递归
        //3
    }
//1.处为前序
//2.处为中序
//3.处为后序  操作数组的位置

2.重新构建一颗二叉树
106. 从中序与后序遍历序列构造二叉树
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector& inorder, vector& postorder) {
        if(inorder.size() == 0 || postorder.size() == 0){
            return nullptr;
        }
        int temp = postorder[postorder.size()-1];
        TreeNode* head = new TreeNode(temp);
        auto ptr = find(inorder.begin(),inorder.end(),temp);
        int mid = ptr-inorder.begin();
        vector il(inorder.begin(),inorder.begin()+mid);
        vector ir(inorder.begin()+mid+1,inorder.end());
        vector pl(postorder.begin(),postorder.begin()+mid);
        vector pr(postorder.begin()+mid,postorder.end()-1);
        head->left = buildTree(il,pl);
        head->right = buildTree(ir,pr); 
        return head;
    }
};
//需要注意数组的拷贝范围，要知道 （begin，end）begin是起始位置，end是结束位置的下一个位置。

3.序列化和反序列化：空处要用标识符标记，将一颗树转换成字符串表示，反序列化是将字符串转换成一颗二叉树
剑指 Offer 37. 序列化二叉树
序列化：用前序遍历，生成字符串。
反序列化：将字符串根据分隔符（逗号），切割成子字符串
需要注意的是，遍历时我们一般用void 返回值，将遍历值保存在数组中
 ，生成树时，一般用树节点作为返回值，
 //遍历的模板
void proess(TreeNode* root,vector& my_vec)
    {
        if(root == nullptr)return ;
        proess(root->left,my_vec);
        my_vec.emplace_back(root->val);
        proess(root->right,my_vec);
    }  


//生成树模板
 TreeNode* preoss(vector& nums,int left,int right){   //递归建立一个二叉树
        if(rightleft = preoss(nums,left,mid-1);  //根据递归规则，如果base case 不满足，这个节点就有值
        head->right = preoss(nums,mid+1,right);
        return head;
    }

根据上面分析：有如下代码：
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Codec {
public:

    //序列化  //遍历的过程 使用前序遍历
    string serialize(TreeNode* root) {
        string  my_str = "";
        proess(root,my_str);
        //my_str.pop_back();
        //std::cout< my_str;
        vector my_str;
        vector index;
        for(int i = 0;i& my_str,int& index)   //建立一颗二叉树，返回树节点
    {
        if(my_str[index] == "null" || index>=(my_str.size()-1))
        {
            return nullptr;
        }
        TreeNode* head = new TreeNode(atoi(my_str[index].c_str()));
        index++;
        head->left = pro(my_str,index);
        index++;
        head->right = pro(my_str,index);
        return head;
    }
    void proess(TreeNode* root, string& my_str)
    {
        if(root == nullptr)
        {
            my_str +="null,";
            return ;
        }
        my_str += std::to_string(root->val); //转换成字符串的格式
        my_str.push_back(',');
        proess(root->left,my_str);
        proess(root->right,my_str);
    }
};
//2021.4.16
// Your Codec object will be instantiated and called as such:
// Codec codec;
// codec.deserialize(codec.serialize(root));

4.BST 搜索二叉树：左节点比根节点小，右节点比根节点大。左子树的最大值比根节点小，右子树的最小值比根节点大。二叉搜索树（BST）的中序遍历是有序的
700. 二叉搜索树中的搜索
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        return proess(root,val);
    }
    TreeNode* proess(TreeNode* root,int val){    //递归
        if(root==nullptr)return nullptr;         //递归到叶节点，还是没有找到，返回空  //递归终止条件
        if(root->val == val){
            return root;                    //找到了 ，直接返回了
        }
        TreeNode* ans = nullptr;
        if(root->val > val){                //利用bst的特性
            ans = proess(root->left,val);   
        }
        if(root->val < val){
            ans = proess(root->right,val);  //如果没有没有找到就会返回空
        }
        return ans;
    }
};
//2021.3.27 使用中序遍历 根据它是一颗bst的这个特性。

考虑好递归怎么去写，递归终止条件。当然也是可以使用迭代法，去处理递归的题目的，递归的空间复杂度比较大。
783. 二叉搜索树节点最小距离
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDiffInBST(TreeNode* root) {
        vector my_vec;
        int min = INT_MAX;
        int zhi = 0;
        proess(root,my_vec);
        //sort(my_vec.begin(),my_vec.end());
        for(int i = 0;izhi?zhi:min;
        }
        return min;
    }
    void proess(TreeNode* root,vector& my_vec)
    {
        if(root == nullptr)return ;
        proess(root->left,my_vec);
        my_vec.emplace_back(root->val);
        proess(root->right,my_vec);
       
    }
};
//2021.4.13 中序遍历 BST用中序遍历

897. 递增顺序搜索树
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* increasingBST(TreeNode* root) {
        vector nums;
        proess(root,nums);
        int zhi = 0;
        //build(root,nums,zhi);
        return build(nums,zhi);
    }
    void proess(TreeNode* head,vector &nums){
        //base case
        if(head == nullptr){
            return;
        }
        //中序遍历
        proess(head->left,nums);
        nums.emplace_back(head->val);
        proess(head->right,nums);
    }
    TreeNode* build(vector &nums,int &index){
        //base case
        if(index == nums.size()){
            return nullptr;
        }
        //处理
        TreeNode* head = new TreeNode(nums[index]);
        head->right = build(nums,++index);
        return head;
    }
};

5.平衡二叉树：左子树和右子树的高度相差小于1
110. 平衡二叉树
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
struct info{
        int height;
        bool isb;
        info(int h,bool is):height(h),isb(is){}
    };   //定义一个类型肯定要在一个类的外面定义呀，类中才可以使用之
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        info ans = proess(root);
        return ans.isb;
    }
    info proess(TreeNode* root){
        if(root == nullptr)return info(0,true);
        
        info leftinfo = proess(root->left);
        info rightinfo = proess(root->right);

        int height = max(leftinfo.height,rightinfo.height)+1;
        bool isb = leftinfo.isb && rightinfo.isb && abs(leftinfo.height-rightinfo.height)<2;

        return info(height,isb);
    }
    
};
//2021.3.31

6.满二叉树：深度h 和 节点个数n 满足：2^h-1 = n
7.求两节点的公共祖先
使用深度优先搜索的做法。模板是死的，方法是活的，模板会帮助快速做题，但也会限制住自己的思路
236. 二叉树的最近公共祖先
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode *ans = nullptr;
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        isans(root,p,q);
        return ans;
    }
    bool isans(TreeNode* head,TreeNode* p,TreeNode* q){
        if(head == nullptr)return false;
        bool leftnode = isans(head->left,p,q);
        bool rightnode = isans(head->right,p,q);
        if(leftnode&& rightnode||(head->val == p->val || head->val == q->val )&& (leftnode ||rightnode)){
            ans = head;
        }
        return leftnode || rightnode || head->val == p->val ||head->val == q->val;
    }
};

 /**
 * struct TreeNode {
 *    int val;
 *    struct TreeNode *left;
 *    struct TreeNode *right;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param root TreeNode类 
     * @param o1 int整型 
     * @param o2 int整型 
     * @return int整型
     */
    TreeNode* dfs(TreeNode* root,int o1,int o2){
        //如果当前节点为空，或者当前节点等于o1或者等于o2就返回值给父亲节点
        if(root == NULL || root->val == o1 || root->val == o2) return root;
        //递归遍历左子树
        TreeNode *left = dfs(root->left,o1,o2);
        //递归遍历右子树
        TreeNode *right = dfs(root->right,o1,o2);
        //如果left、right都不为空，那么代表o1、o2在root的两侧，所以root为他们的公共祖先
        if(left != NULL && right != NULL) return root;
        //如果left、right有一个为空，那么就返回不为空的哪一个
        return left != NULL? left : right;

    }
    int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
       return dfs(root,o1,o2)->val;
    }
};


8.求前驱或者后继节点 ：前驱后继指的是中序遍历中的顺序
9.宽度优先遍历：需要用到到queue这个结构辅助
模板：利用到队列，弹出一个，压入两个，迭代起来就可以实现宽度优先遍历
if(root == nullptr)return ans;  //清除无效数据
        queue my_queue;
        my_queue.push(root);
        TreeNode* zhi = nullptr;
        //ans.push_back(mid);
        while(!my_queue.empty()){
            zhi = my_queue.front();
            my_queue.pop();             //从队列中弹出
            std::cout<val<left!=nullptr){
                my_queue.push(zhi->left);
            }
            if(zhi->right!=nullptr){
                my_queue.push(zhi->right);
            }
        }

记录层数、最宽一层的节点个数----->利用辅助容器，哈希表（比较复杂）–》更加优的方案：每次压入下一层节点之前。把队列中的元素个数记录下来，然后下一轮就弹出所记的个数次，这种方法更加优秀。
每个节点进队列的时候记录层数，下一层的就用哈希表查询上一层的层数（用键值），unordered_map中的find传入的是键值，返回的是迭代器，这个迭代器的第一个值就是key,第二值就是value。查询后就得到上一层的层数，下一层的节点同理压入到哈希表中。具体如下：
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        vector> ans;
        if(root == nullptr)return ans;  //清除无效数据
        queue my_queue;       //队列
        unordered_map level;     //定义一个哈希表  第一个参数是key,第二个是value
        level.emplace(root,1); //
        int ceng = 0;      //层数
        my_queue.push(root);
        TreeNode* zhi = nullptr;
        while(!my_queue.empty()){
            zhi = my_queue.front();        //队列中的第一个值
            auto ptr = level.find(zhi);   //返回的是查询得到的迭代器
            ceng = ptr->second;           //第二值是value
            my_queue.pop();
            //std::cout << zhi->val << ' ' << ceng << std::endl;
            if(zhi->left!=nullptr){
                my_queue.push(zhi->left);
                level.emplace(zhi->left,ceng+1);   //插入到哈希表中，层数加一
            }
            if(zhi->right!=nullptr){
                my_queue.push(zhi->right);
                level.emplace(zhi->right,ceng+1);
            }
        }
        return ans;
    }
};
//2021.3.27  宽度优先遍历  ： 队列做辅助容器 迭代法

剑指 Offer 32 - II. 从上到下打印二叉树 II
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        vector> ans;
        if(root == nullptr)return ans;  //清除无效数据
        queue my_queue;       //队列
        unordered_map level;     //定义一个哈希表  第一个参数是key,第二个是value
        level.emplace(root,1); //
        int ceng = 0;      //层数
        my_queue.push(root);
        vector mid;
        //mid.push_back(root->val);
        TreeNode* zhi = nullptr;
        //ans.push_back(mid);
        int nums = 1;
        while(!my_queue.empty()){
            zhi = my_queue.front();
            auto ptr = level.find(zhi);
            ceng = ptr->second;                          //层数相关操作
            my_queue.pop();
            //std::cout << zhi->val << ' ' << ceng << std::endl;
            if(nums!=ceng){                              //保存到数组中
                nums++;
                ans.push_back(mid);
                mid.clear();
                mid.push_back(zhi->val);
            }
            else{
                mid.push_back(zhi->val);
            }
            if(zhi->left!=nullptr){    //宽度优先遍历
                my_queue.push(zhi->left);
                level.emplace(zhi->left,ceng+1);
            }
            if(zhi->right!=nullptr){
                my_queue.push(zhi->right);
                level.emplace(zhi->right,ceng+1);
            }
        }
        ans.emplace_back(mid);    //将最后的数组压入
        return ans;
    }
};
//2021.3.27  宽度优先遍历  ： 队列做辅助容器 迭代法

用到了哈希表、队列，动态数组，所以空间复杂度会挺大的。迭代法，用额外容器栈辅助
9.完全二叉树：不存在只有右子树没有左子树的情况。如果孩子不双全，那么后面的节点都是叶几点。
1382. 将二叉搜索树变平衡
/**
 * Definition for a binary tree node.
 * struct TreeNode { 
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* balanceBST(TreeNode* root) {
        //1.将搜索树中的数据b保存在一个数组中  递归法  中序遍历
        vector nums;
        bianli(root,nums);
        return preoss(nums,0,nums.size()-1);
       /* for(auto i:nums){
            std::cout<& nums){    //遍历
        if(root == nullptr){
            return ;   //返回空，意思是结束，返回了
        }
        bianli(root->left,nums);
        nums.push_back(root->val);
        bianli(root->right,nums);   //中序遍历  递归
    }
    TreeNode* preoss(vector& nums,int left,int right){   //递归建立一个二叉树
        if(rightleft = preoss(nums,left,mid-1);
        head->right = preoss(nums,mid+1,right);
        return head;
    }
};
//2021.3.26 法一 暴力法 = 分治+递归

剑指 Offer 26. 树的子结构
此题分两步走，第一步找根节点，找到根节点再递归，寻找B的子结构是否相同。
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        if(B == nullptr) return false; // 去除无效数据
        bool ans = false;
        proess(A,B,B->val,ans);
        return ans;
    }
    void proess(TreeNode* A ,TreeNode*B,int num,bool& flag)
    {
        if(A == nullptr) return ;
        if(A->val == B->val)flag = chuli(A,B);   //前序遍历 ，寻找相同根节点 ，若相同，进递归
        proess(A->left,B,num,flag);
        proess(A->right,B,num,flag);
    }
    bool chuli(TreeNode* roota,TreeNode* rootb)
    {
        if(rootb == nullptr)return true;
        if(roota == nullptr)return false;
        if(roota->val != rootb->val) return false;    //不符合马上退出
        bool flag1 = chuli(roota->left, rootb->left);
        bool flag2 = chuli(roota->right, rootb->right);  //采用前序遍历的方法，不断递归
        return flag1&&flag2;   //将左右节点的返回值，并起来，得到最终结果
    }
};
//2021.4.6 题不在多，而是在精

深度优先搜索（DFS）
104. 二叉树的最大深度
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr)return 0;
        int max = 0;
        int height = 0;
        dfs(root,height,max);
        return max;
    }
    void dfs(TreeNode* head, int &height,int &max){
        if(head == nullptr){
            return ;
        }
        height++;
        max = height>max?height:max;
        dfs(head->left,height,max);
        dfs(head->right,height,max);
        height--;
    }
};
//2021.6.13

位运算
位运算这一块，会的就很简单，不会的话，就算是简单题，也是困难题
左移：>>
右移：<<
位与：&
位或：|
异或：^
190. 颠倒二进制位
cclass Solution {
public:
    uint32_t reverseBits(uint32_t n) {
        uint32_t ans = 0;
        for(int i = 0;i<32;i++){
            ans = (ans<<1)+(n&1);    //y移动，+的b部分就室加在后面
            n = n>>1;                 //左移
        }
        return ans;
    }
};
//2021.3.29位运算

9. 回文数
class Solution {
public:
    bool isPalindrome(int x) {        
		if(x<0)return false;
        long  y = 0;  //如果y用int定义的话，下面*10会c越界，
        int flag = x;
        while(x!=0){
            y = y*10+x%10;  //*10就是相当于整数右移 后加就是补充部分
            x = x/10;    //相当于整数左移
        }
        if(flag == y)return true;
        return false;
    }
};

504. 七进制数
此类题型，涉及到位运算，/表示左移 *表示右移，%则可以提取对应的位。
class Solution {
public:
    string convertToBase7(int num) {
        if(num == 0)return "0";
        bool flag = true;
        if(num<0){
            flag = false;
            num = abs(num);
        }
        string temp = "0123456";
        string ans;
        while(num !=0){
            ans.push_back(temp[num%7]);
            num /=7;
        }
        reverse(ans.begin(),ans.end());
        if(!flag)ans = "-"+ans;
        return ans;
    }
};
//2021.6.7

进制转换
描述
给定一个十进制数M，以及需要转换的进制数N。将十进制数M转化为N进制数

class Solution {
public:
    /**
     * 进制转换
     * @param M int整型 给定整数
     * @param N int整型 转换到的进制
     * @return string字符串
     */
    string solve(int M, int N) {
        // write code here
        if(M == 0)return "0";
        bool flag = true;
        if(M<0){
           flag = false; 
           M = abs(M);
        }
        string temp = "0123456789ABCDEF";
        string mid;
        while(M != 0){
            mid.push_back(temp[M%N]);
            M /= N;
        }
        string ans;
        for(int i = mid.size()-1;i>=0;i--){
            ans.push_back(mid[i]);
        }
        if(!flag)ans.insert(0,"-");
        return ans;
    }
};

滑动窗口
class Solution {
public:
    vector maxSlidingWindow(vector& nums, int k) {
        int left = 0;
        int right = 0;
        deque my_deque;
        vector ans;
        if(nums.size() == 0)return ans;
        while(right=nums[my_deque.back()])my_deque.pop_back();
            my_deque.push_back(right);
            right++;
        }
        ans.emplace_back(nums[my_deque.front()]);
        while(right=nums[my_deque.back()])
            //{
                while(!my_deque.empty() && nums[right]>=nums[my_deque.back()])my_deque.pop_back();
                my_deque.push_back(right);
            //}
            //if(my_deque.empty())my_deque.push_back(right);
            ans.emplace_back(nums[my_deque.front()]);
            right++;
        }
        return ans;
    }
};
//2021.4.3  滑动窗口

用deque,单调栈，存放index
生成窗口最大值数组
描述
有一个整型数组arr和一个大小为w的窗口从数组的最左边滑到最右边，窗口每次向右边滑一个位置，求每一种窗口状态下的最大值。（如果数组长度为n，窗口大小为w，则一共产生n-w+1个窗口的最大值）
输入描述：
第一行输入n和w，分别代表数组长度和窗口大小
第二行输入n个整数XiX_iXi，表示数组中的各个元素
输出描述：
输出一个长度为n-w+1的数组res，res[i]表示每一种窗口状态下的最大值
输入：

8 3
4 3 5 4 3 3 6 7

输出：
5 5 5 4 6 7
说明：
例如，数组为[4，3，5，4，3，3，6，7]，窗口大小为3时：
[4 3 5] 4 3 3 6 7        窗口中最大值为5
4 [3 5 4] 3 3 6 7        窗口中最大值为5
4 3 [5 4 3] 3 6 7        窗口中最大值为5
4 3 5 [4 3 3] 6 7        窗口中最大值为4
4 3 5 4 [3 3 6] 7        窗口中最大值为6
4 3 5 4 3 [3 6 7]        窗口中最大值为7
输出的结果为{5 5 5 4 6 7}

#include 

using namespace std;

int main()
{
    int n,w;
    cin>>n>>w;
    vector vec;
    for (int i = 0;i>temp;
        vec.emplace_back(temp);
    }
    deque sing;
    for (int i = 0;ivec[i])
            {
                while(vec[sing.back()](w-1))sing.pop_front();
            if(vec[sing.front()]>vec[i])
            {
                while(vec[sing.back()]

using namespace std;

int main()
{
    int n,w;
    cin>>n>>w;
    vector vec;
    for (int i = 0;i>temp;
        vec.emplace_back(temp);
    }
    deque sing;
    for (int i = 0;i(w-1))sing.pop_front();
            
                while(!sing.empty()&&vec[sing.back()]

using namespace std;

int main()
{
    int n,w;
    cin>>n>>w;
    vector vec;
    for (int i = 0;i>temp;
        vec.emplace_back(temp);
    }
    deque sing;
    sing.push_back(0);
    for (int i = 1;i(w-1))sing.pop_front();
                while(!sing.empty()&&vec[sing.back()]=(w-1))
        cout<

数组、字符串
给定一个 mmm 行、nnn 列的矩阵，请按照顺时针螺旋的顺序输出矩阵中所有的元素（从[0][0]位置开始，具体请参见下图）。

输入格式
测评机会反复运行你写的程序。每次程序运行时，首先在第一行输入 222 个整数，分别对应题目描述中的 mmm 和 nnn（1≤m,n≤1001 \leq m,n \leq 1001≤m,n≤100），之间用一个空格分隔。接下来输入 mmm 行，每行包含 nnn 个整数（−10000≤a,b,c≤10000-10000 \leq a, b, c \leq 10000−10000≤a,b,c≤10000），每两个整数之间用一个空格分隔。
输出格式
输出为一行，包括 m×nm\times nm×n 个整数，按照题目要求的顺序依次输出所有矩阵元素，任意两个整数之间用一个空格分隔，最后一个整数后面没有空格。
#include 
int cnt = 0;
int matrix[100][100];    
int m;
int n;
int printf_matrix(int i,int j)
{
    printf("%d",matrix[i][j]);
    cnt++;
    if(cnt == n*m)return 1;
    printf(" ");  //就不输出空格了
    return 0;
}
int main() {
    

    scanf("%d %d",&m,&n);
    for(int i =0;i=l;j--)  //从左到右
        {
            flag = printf_matrix(i,j);
            if(flag == 1)break;
        }
        b--; //下边界减减
        if(flag == 1)break;
        for(i = l,j=b;j>=t;j--)  //从下到上
        {
            flag = printf_matrix(j,i);
            if(flag == 1)break;
        }
        l++;//左边界加加 
        if(flag == 1)break;
    }
    printf("\n");
    return 0;
}

二维数组的操作，将一个大循环拆成4个
179. 最大数
给定一组非负整数 nums，重新排列每个数的顺序（每个数不可拆分）使之组成一个最大的整数。
注意：输出结果可能非常大，所以你需要返回一个字符串而不是整数。
示例 1：
输入：nums = [10,2]
 输出：“210”
示例 2：
输入：nums = [3,30,34,5,9]
 输出：“9534330”
示例 3：
输入：nums = [1]
 输出：“1”
示例 4：
输入：nums = [10]
 输出：“10”
提示：
1 <= nums.length <= 100
0 <= nums[i] <= 109

class Solution {
public:
    string largestNumber(vector& nums) {
        //vector ans;
        priority_queue,cmp> ans;
        string my_ans;
        for(int i = 0 ;i

c中的scanf(),gets(),的读取速度比cin,getline,速度更加快快，cin,cout的速度比scanf和printf速度慢
scanf不能接受空格、制表符Tab、回车等；
而gets能够接受空格、制表符Tab和回车等； 这两个函数都在stdio.h,头文件中。
sprintf() 可以被我们广泛地应用于各种数据的格式化，第一个参数是被写入的字符串，第二个参数是写入的格式，之后的参数是依次回被写入的数据。
sprintf(information,"%s is a %s. He is %d-year-old and %fcm tall.",name,gender,age,height);

strlen() //返回字符串的长度
strcpy(目的，源) //字符串拷贝 在string.h这个头文件中
strcmp()函数用于比较两个字符串的大小 strcmp(input,string);.返回值小于0，则inputstring;
strcat ：函数将第二个参数的字符串（含\0）拷贝到第一个参数的字符串\0所在的内存位置之后。
strcat：将字符串连接在另一字符串后
strncpy：复制某一字符串的前 nnn 个字符到另一字符串
strcpy：复制某一字符串到另一字符串
strcmp：对字符串进行比较
strlen：获得字符串的长度
前缀树-查、建操作
208. 实现 Trie (前缀树)
构建一个多叉树，这种数据结构在前缀时，非常便利。
1.每一次插入数据时就是在新建这颗树的枝叶。
2.寻找查找，寻找前缀，都是对这颗树的枝叶的遍历。
struct node{
        int pass;
        int end;
        node* next[26] = {nullptr};  //初始化为0
        node(int a,int b):pass(a),end(b){
        }
    };  //自己定义一个结构体，，需要定义在类外
class Trie {
    public:
    Trie() {
       //memset(node_shou, 0,sizeof(struct node));
       node_shou = new node(0,0);  //初始化首节点
    }
    /** Inserts a word into the trie. */
    void insert(string word) {
        node* node_1 = node_shou; //首节点
        for(int i = 0;inext[index] != nullptr)  //不为空
            {
                node_1->next[index]->pass++;
                if(i==word.size()-1)node_1->next[index]->end++;
            }
            else{//创建
                if(i == word.size()-1)node_1->next[index] = new node(1,1);
                else
                node_1->next[index] = new node(1,0);
            }
            node_1 = node_1->next[index];
        }
    }
    /** Returns if the word is in the trie. */
    bool search(string word) {
        node* node_2 = node_shou;
        for(int i = 0;inext[index] != nullptr)
            {
                if(i == word.size()-1){
                    if(node_2->next[index]->end != 0)return true;
                    else 
                        return false;
                }
            }else{
                return false;
            }
            node_2 = node_2->next[index];
        } 
        return true;
    }
    /** Returns if there is any word in the trie that starts with the given prefix. */
    bool startsWith(string prefix) {
        node* node_3  = node_shou;
        for(int i = 0;inext[index] != nullptr)
            {
                if(i == prefix.size()-1){
                    if(node_3->next[index]->pass != 0)return true;
                    else 
                        return false;
                }
            }else{
                return false;
            }
            node_3 = node_3->next[index];
        }
        return true;
    }
private:
    node* node_shou;  //首节点
};

自定义的数据类型，如类，结构体，都必须定义在类外。这题只有26个小写字符，所以用数据表示next就行，如果，数据量过大，就得使用哈希表，这种结构，时间，空间复杂度都会得到优化。
648. 单词替换
typedef struct node{
    int pass;
    int end;
    //bool flag = false;       //判断是否结束
    struct node* next[26] = {nullptr};
    node(int a,int b):pass(a),end(b){}
}Node;
class Solution {
public:
    Solution() //构造函数
    {
        node_shou = new Node(0,0);
    }
    string replaceWords(vector& dictionary, string sentence) {
        //建立前缀树
        build_trie(dictionary);
        //将句子切分
        vector mystr;
        vector biaoding;
        for(int i = 0;inext[index] != nullptr )
            {
                if(node_2->next[index]->pass != 0)out.push_back(words[i]);
                if(node_2->next[index]->end != 0)return out;
            }
            else
            {
                return words;
            }
            node_2 = node_2->next[index];       
        }
        return words;
    }
    void build_trie(vector& dictionary)   //建树
    {
        for(int i = 0;inext[index] == nullptr)//为空
            {
                if(i  == str.size()-1)node_1->next[index] = new Node(1,1); 
                else
                    node_1->next[index] = new Node(1,0); 
            }
            else//不为空
            {
                if(i == str.size()-1)
                {
                    node_1->next[index]->end++;
                }
                node_1->next[index]->pass++;
            }
            node_1 = node_1->next[index];
        }
    }
    
private:
    Node* node_shou;
};

这道题也是一道前缀树类型的题目。主要在于如何去利用这个数据结构，这个结构的主要操作是，建树、查找。
要处理的地方在于怎么迁移到这道题目上面来。
观察题意，我们可以用pass 和end 来辅助处理。如何理解？
首先是建树，建树的过程和上一道的前缀树是一样的（当然在处理之前，要思考，是字典作为树，还是句子中的单词作为树），用句子中单词建树，数据量会很大，而且有多余的部分（分析实例，其中有很多没有词根的是直接输出的，因此我们建树的话，待会这个树会很庞大，且很多枝干是多余的存在的），反过来看，用词根建树，每个词根在树中是有存在的意义的。用句子中的单词在这颗树中查询。效率很高很多，比如首字母就查找不到，直接退出！
其次，如何用上pass end ，pass 代表词根中有经过这个字母，end代表词根中有以此字母为结束的（是遍历每个词根中的每个字母，建树的过程）
第三将句子中的单词提取出来。
第四，在建好的词根树中，查询每个单词。pass不为0时，加入到一个新的字符串中（加入到尾部），如果end不为0 ，说明词根存在，赶紧输出前面的新字符串中。
第五，如果没有找到词根（其中包括，1.首字母就不匹配。2.词根前部分匹配，后半部分不匹配），则输出原来的单词。
基本数学
1.求质数；
质数的定义：质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。否则称为合数。
求质数就有三种方法：
1.定义法：
#include 
int main() {
    int zhi;
    int num;
    int mid;
    scanf("%d",&zhi);
    if(zhi>=2)
    {
        printf("%d\n",2);   //2先输出
    }
    for(num = 3;num<=zhi;num+=2)  //除了外没有质数是偶数了
    {
        for(mid = 2;mid

2.奇数筛：质数中，2是唯一的偶数。
#include 
int main() {
    printf("2\n");  //输出2
    int digit;
    int divisor;
    for (digit = 3; digit <= 15; digit += 2) {  //2是唯一的偶数，
        for (divisor = 3; divisor < digit; divisor += 2) {
           if(digit % divisor ==0)//奇数，不能被偶数筛选
           {
               break;
           }
        }
          if(digit == divisor)
           {
               printf("%d\n",digit);
           }
    }
    return 0;
}

3.质数筛法：牺牲空间，换取速度
用筛法求素数的基本思想是：把从2到N的一组正整数从小到大按顺序排列。从中依次删除2的倍数、3的倍数、5的倍数，直到根号N的倍数为止，剩余的即为2~N之间的所有素数。如有：
2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
去掉2的倍数（不包括2），余下的数是：
3 5 7 9 11 13 15 17 19 21 23 25 27 29
剩下的数中3最小，去掉3的倍数，如此下去直到所有的数都被筛完，求出的素数为：
2 3 5 7 11 13 17 19 23 29
1 <=c**c <= n 因为后面回用倍数去筛，所以不用到最大到c*c
void judge_prime()
{
    init();
    for(int i = 2;i*i<100;++i)  //将i的倍数，从100中筛掉，所以最大只能到10*10
    {
        if(is_prime[i] == 1)  //代表数还没被筛掉，进入
        {
            for(int j = i*i;j<100;j+=i) //i的倍数，全部筛掉  j+=i就是实现倍数
            {
                is_prime[j] = 0;   
            }
        }
    }
}

    for (c = 2; c * c <= n; c++) {      //另一种做法
		if(mark[c]!=1)
        {
            for(j=2;j<=n/c;j++)
            {
                mark[c*j] =1;
            }
        }
    } // 也是同样的做法

2.求最大公因数、最小公倍数
我们学习了函数和函数的递归调用后，我们可以用它们来实现一个求两个整数最大公因数和最小公倍数的程序。
我们都知道，对于两个整数 n,mn,mn,m，它的最大公因数 gcd(n,m)\mathrm{gcd}(n,m)gcd(n,m) 是 nnn 和 mmm 最大的公共因数。我们可以通过 辗转相除法 的方式将它求出。
而最小公倍数 lcm(n,m)\mathrm{lcm}(n,m)lcm(n,m) 则是 nnn 和 mmm 的公共倍数中最小的数。可以通过下面的式子求出：
  $l c m (n, m) = (n * m) / g c d (n, m);$ 
 在这里，你完成的程序将被输入两个正整数 nnn 和 mmm（你可以认为测评机给出的 nnn 和 mmm 均小于 100010001000），程序需要求出 nnn 和 mmm 最大公因数和最小公倍数，并把它们输出出来。
输入格式
测评机会反复运行你的程序。每次程序运行时，输入为一行，包括一组被空格分隔开的符合描述的正整数 mmm 和 nnn。
输出格式
输出为两行，每行为一个数字。第一行为 nnn 和 mmm 的最大公因数，第二行为 nnn 和 mmm 的最小公倍数。
辗转相除法：求两个正整数最大公约数的算法

欧几里得算法是用来求两个正整数最大公约数的算法。古希腊数学家欧几里得在其著作《The Elements》中最早描述了这种算法,所以被命名为欧几里得算法。
扩展欧几里得算法可用于RSA加密等领域。
假如需要求 1997 和 615 两个正整数的最大公约数,用欧几里得算法，是这样进行的：
1997 / 615 = 3 (余 152)
615 / 152 = 4(余7)
152 / 7 = 21(余5)
7 / 5 = 1 (余2)
5 / 2 = 2 (余1)
2 / 1 = 2 (余0)
至此，最大公约数为1
以除数和余数反复做除法运算，当余数为 0 时，取当前算式除数为最大公约数，所以就得出了 1997 和 615 的最大公约数 1。


#include 
int gcd(int n, int m);
int lcm(int n, int m);
int main() {
    int n, m;
    scanf("%d%d", &n, &m);  
    printf("%d\n", gcd(n, m));
    printf("%d\n", lcm(n, m));
    return 0;
}
int gcd(int n, int m) {
    if (m <= n) {
    // 请在这里继续完成 gcd 函数
    int mid = m;
    int yu = n%mid;
    int n = mid;
    m = yu;
    if(yu == 0)return mid;
    else 
        return gcd(n,m);
    } else {
        return gcd(m, n);  //递归
    }
}
int lcm(int n, int m) {
// 请在这里继续完成 lcm 函数
  return (n*m)/gcd(n,m);
}

并查集
1.概念
对集合的操作：1.合并集合 2.搜索两元素是否再同一个集合中
利用并查集这种数据结构 可以实现上面这两个操作的时间复杂度均为O1
经典应用：最小生成树 , 无向连通块的数量。
树中的每个节点有两部分组成：数值加父节点。用一个数组表示这个节点，如P[i] = a 这里的i就是数值，a就是父节点。一开始节点的父节点都是指向自己的。
路径压缩：使得集合合并的时间复杂度变为O1。就是将所有的父节点反向指向其领导。后续的查询的速度就会变成O1;
const int N = 1e5+10;//根据题意可调整，尽量预留大一些
int parent[N];       //父节点   //就是并查集
//查操作 -- 反向路径压缩
int find(int x)
{
    if(parent[x] != x) parent[x] = find(parent[x]);  //不同，说明要找到他的领导
    return x;  //如果父节点就是他自己，就返回自身节点。
    //retrurn parent[x]!=x?x=find(parent[x]):x
}

//并操作
void to_uion(int i,int j)
{
    parent[find(j)] = find(i);  //表示j 的领导改为i 的领导，这样的话就实现的合并的操作了
}

class Find_union{
    public:
    	Find_union() 
        {
            for(int i = 1;i

2020年 真题 地铁打卡
地铁迷在某个城市组织了地铁打卡活动。活动要求前往该城市中的所有地铁站进行打卡。打卡可以在站外或者站内进行。地铁的计价规则如下：只要不出站，就不计费；出站时，只计算进站和出站站点的距离。如在同一个站点进出站，按照最低票价 a 元计算。假设地铁票不会超时。大部分站点都是通过地铁线连通的，而且地铁站的连通是双向的（若 A，B 连通，则 B，A连通），且具有传递性的（若 A，B 连通，且 B，C 连通，则 A，C连通）。但并不是所有的地铁站都相互连通，在不能通过坐地铁达到的两个地点间，交通的花费则提高到 b 元。地铁迷从酒店起点出发，再回到酒店。假设从酒店到达任意地铁站的交通花费为 b 元。请计算地铁迷完成打卡最小交通花费。

每组输入包括m + 1行。第1行包含4个整数n，m，a，b，其中n表示地铁站点数，m表示连通的地铁站点对数，a代表地铁最低票价，b代表非地铁方式票价，其中0 < a < b。第2到m + 1行，每行2个整数Hi，Ti代表站点Hi和Ti站点是连通的（0 <= i< m）。
8 7 3 6
0 1
1 2
2 3
0 3
4 5
5 6
4 7

输出只有一行，包含一个整数，表示打卡的最小交通花费。

24

#include 

using namespace std;


const int N = 1e5+50;
int parent[N];
int n,m,a,b;
int h,t;

int find(int x)
{
    if(parent[x] != x)parent[x] = find(parent[x]);
    return parent[x];
}

void to_union(int i, int j)
{
    parent[find(i)] = find(j);
}

int main()
{
    cin>>n>>m>>a>>b;
    for(int i = 0;i>h>>t;
        to_union(h,t); // 合并        合并后有两个不连通的块
    }
    int size = 0;
    for(int k = 0;k

在解上面这道题的时候，我陷入了一个误区，因为前面讲的路径压缩，我以为最终，合并后的的parent[n]中的值的类别会是块的数量。实际上，根据确认领导的原则，我们知道parent[k] = k;k才是领导，而后面的合并如果出现直接领导与领导合并，而没有没有从出现原来集合中元素再并入的情况，这是是不会有路径压缩。从这个过程中我们也可以知道路径压缩时出现在什么时候：最低端的节点后续合并时，才会出现路径压缩。
547. 省份数量
有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。


输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2


输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

class Solution {
public:
    int find(int x)
        {
            if(p[x] != x) p[x] = find(p[x]);
            return p[x];
        }
    void to_union(int i , int j)
        {
            p[find(i)] = find(j);
        }
    int findCircleNum(vector>& isConnected) {
        //确定城市数量，初始化并查集
        for(int i = 0;i

1319. 连通网络的操作次数
用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b。

网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。

给你这个计算机网络的初始布线 connections，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。 



输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。


输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
输出：2

输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
输出：-1
解释：线缆数量不足。

输入：n = 5, connections = [[0,1],[0,2],[3,4],[2,3]]
输出：0

提示：
	1 <= n <= 10^5
	1 <= connections.length <= min(n*(n-1)/2, 10^5)
	connections[i].length == 2
	0 <= connections[i][0], connections[i][1] < n
	connections[i][0] != connections[i][1]
	没有重复的连接。
	两台计算机不会通过多条线缆连接.

class Solution {
public:
    int makeConnected(int n, vector>& connections) {
        //判断线缆数够不够
        if(n-1>connections.size())return -1;
        //根据计算机数量，初始化并查集
        for(int i = 0 ;i

/** 滴滴二面代码题：
*       输入：[1, 5, 7, 3, 9, 8, 10]
* [(1, 3), (5, 7), (7, 1), (9, 8)]
* --表示1和3有关，5和7有关，7和1有关，9和8有关。
*       输出：[(1, 3, 7, 5), (8, 9), (10)]*/

#include 
#include 
#include 
#include 
using namespace std;

const int N = 1e5;
int p[N];

int find(int x)
{
	if (p[x] != x) p[x] = find(p[x]);
	return p[x];
}

void to_union(int i,int j)
{
	p[find(i)] = find(j);
}

int main()
{
	vector myvec = {1,5,7,3,9,8,10};
	unordered_set hs;
	
	
	for (int i = 0;i< myvec.size();i++)
	{
		hs.emplace(myvec[i]);
	}
	sort(myvec.begin(), myvec.end());
 
	for (int i = 0;i<=myvec[myvec.size()-1];i++)
	{
		p[i] = i;
	}

	vector> in2 = { {1,3},{5,7},{7,1},{9,8} };
	for (int i = 0;i leader;
	for (int i = 0;i<=myvec[myvec.size()-1];i++)
	{
		if (hs.find(i) != hs.end() && p[i] == i)
		{
			leader.push_back(i);
		}
	}
	vector> out;
	vector mid;
	for (int k = 0; k < leader.size(); k++)
	{
			for (int i = 0; i <= myvec[myvec.size() - 1]; i++)
			{
				if (find(i)== leader[k])
				{
					mid.push_back(i);
					cout << i << ' ';
				}
			}
			out.emplace_back(mid);
			mid.clear();
			cout << endl;
	}
	//cout << p[5] << endl;
	return 0;
}

695. 岛屿的最大面积
给定一个包含了一些 0 和 1 的非空二维数组 grid 。

一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

class Solution {
public:
    //并
    void to_union(int a,int b)
    {
        p[myfind(a)] = myfind(b);
    }
    //查
    int myfind(int x)
    {
        if (p[x]!=x)p[x] = myfind(p[x]);
        return p[x];
    }
    int maxAreaOfIsland(vector>& grid) {
        //初始化
        const int row = grid.size();
        const int col = grid[0].size();
        for (int i = 0;i hstable;
        for (int i = 0;i

暴力递归（回溯）：DFS算法
一般的问题是：求所有的可行解；而动态规划的题目一般都是求最优解；
概念：一种暴力穷举算法。穷举的过程就是遍历一颗多叉树的过程。
回溯法非常适合由多个步骤组成的问题，并且每个步骤都有多个选项。在某一步有n个可能的选项，那么该步骤可以看成是树状结构的一个结点，每个选项看成树中节点连接线，经过这些连接线到达该节点的n个子节点。树的叶节点对应着终结状态。如果在叶节点，的状态满足题目的约束条件，那么我们找到了一个可行的解决方案。
回溯算法的代码框架喝多叉树遍历的代码框架类似；
//回溯算法框架
vector result;
void backtrack(路径，选择列表)
{
    if(满足结束条件)    //base case
    {
        result.push_back(路径);
        return;
    }
    for(选择：选择列表)
    {
        做选择；
        backtrack(路径，选择列表);  //这里的选择列表需要根据实际题目做修改
        撤销选择；
    }
}

//多叉树的遍历代码框架
void traverse(TreeNode root)
{
    if(root == nullptr)return ;
    for(TreeNode child:root.children){
        traverse(child);
    }
}

1.汉诺塔问题：
定义：必须是小压大
2.全排列问题
剑指 Offer 38. 字符串的排列
class Solution {
public:
    vector permutation(string s) {
        vector ans;
        vector biaoding(s.size(),false);  //注意这个数组的作用
        unordered_set hs;
        string mid;
        backtrack(s,ans,mid,biaoding,hs);
        return ans;
    }
    void backtrack(string &s,vector &ans, string & mid ,vector &biaoding,unordered_set &hs)
    {
        //base case
        if(mid.size() == s.size()){
            if(hs.find(mid) == hs.end())
            {
                ans.push_back(mid);
                hs.emplace(mid);
            }
            return ;
        }
        //候选条件
        for(int i = 0;i

46. 全排列
class Solution {
public:
    vector> permute(vector& nums) {
        vector bd(nums.size(),false);
        vector> ans;
        vector mid;
        backtrack(nums,mid,ans,bd);
        return ans;
    }
    void backtrack(vector &nums,vector &mid,vector>& ans,vector& bd)
    {
        //base case
        if(nums.size() == mid.size()){
            ans.emplace_back(mid);
            return ;
        }
        //候选条件
        for(int i = 0;i

二维平买面的dfs
完成「力扣」第 130 题：被围绕的区域（中等）；深度优先遍历、广度优先遍历、并查集。
 完成「力扣」第 200 题：岛屿数量（中等）：深度优先遍历、广度优先遍历、并查集；
 完成「力扣」第 417 题：太平洋大西洋水流问题（中等）：深度优先遍历、广度优先遍历；
 完成「力扣」第 1020 题：飞地的数量（中等）：方法同第 130 题，深度优先遍历、广度优先遍历；
 完成「力扣」第 1254 题：统计封闭岛屿的数目（中等）：深度优先遍历、广度优先遍历；
 完成「力扣」第 1034 题：边框着色（中等）：深度优先遍历、广度优先遍历；
动态规划
动态规划的特点：
1.重叠子问题； (动态规划题型的特点)当我们在递归地寻找每个子问题的最优解的时候，有可能会重复地遇到一些更小的子问题，而且这些子问题会重叠地出现在子问题里，出现这样的情况，会有很多重复的计算，动态规划可以保证每个重叠的子问题只会被求解一次。当重复的问题很多的时候，动态规划可以减少很多重复的计算。
2.状态转移方程；
3.最优子结构；（动态规划 题型的特点）当我们在求一个问题最优解的时候，如果可以把这个问题分解成多个子问题，然后递归地找到每个子问题的最优解，最后通过一定的数学方法对各个子问题的最优解进行组合得出最终的结果。
题型：1.求最值；2.穷举
总结： 解决动态规划问题最难的地方有两点：
如何定义 f(n)f(n)f(n)
如何通过 f(1)f(1)f(1), f(2)f(2)f(2), … f(n−1)f(n - 1)f(n−1) 推导出 f(n)f(n)f(n)，即状态转移方程

解题套路：
1.明确状态；2.明确选择；3.明确dp函数和数组的含义；4.明确base case;
状态定义 就是定义子问题，如何表示目标规模的问题和更小规模的问题。例如常见的方法：定义状态 dp[n]，表示规模为 nnn 的问题的解，dp[n - 1] 就表示规模为 n−1n - 1n−1 的子问题的解。在实战中 dp[n] 的具体含义需要首先整理清楚再往下做。
状态转移 就是子问题之间的关系，例如定义好状态 dp[n]，此时子问题是 dp[n-1] 等，并且大规模的问题的解依赖小规模问题的解，此时需要知道怎样通过小规模问题的解推出大规模问题的解。这一步就是列状态转移方程的过程。一般的状态转移方程可以写成如下形式
按照状态定义和状态转移的常见形式，可以对动态规划进行分类，线性、区间、树形
线性动态规划的主要特点是状态的推导是按照问题规模 i 从小到大依次推过去的，较大规模的问题的解依赖较小规模的问题的解 dp[n]的问题
按照问题的输入格式，线性动态规划解决的问题主要是单串，双串，矩阵上的问题，因为在单串，双串，矩阵上问题规模可以完全用位置表示，并且位置的大小就是问题规模的大小。因此从前往后推位置就相当于从小到大推问题规模。
//动态规划解法代码框架
//初始化 base case
dp[0][0][...] = base;
//进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：     //穷举状态
        for ...
            dp[状态1][状态2][....] = 求最值 （选择1 ，选择2 ，，，）  //状态转移

详细的做题步骤：
1.判断题意是否找到一个问题的最优解；
2.判断问题是否能切分为小问题，小问题是否能切为更加的子问题；
3.定义dp,找到状态转移方程；1.明确状态；2.明确选择；3.明确dp函数和数组的含义；4.明确base case;
4.判断边界条件
5.写代码
空间压缩问题：
用一个一维数组代替二维数组，使得空间得到优化
四个出题模型
1.左->右（背包问题）
2.范围问题（回文问题）
博弈问题
3.样本问题（最长公共子序列）
4.分支限界
设计思路（原则）：
1.可变参数最好是一个整数
f（int a,int b）这样的话就可以推出一张二维数组。但是如果是f(int a ,vector b),那么推出来是什么东西呢
一般来说都是这种一个整数的问题模型（所有题型都要往这个方向发展），tsp问题（复杂度很高）是另一个一系列可变问题组成的
2.尽量使用少个可变参数的个数
2个就是2维表，3个就是3维表。。。。
题型：
1.机器人运动问题
a.N 1-N格子
b. start 机器人开始时的位置
c. end 机器人要去哪（目的）
d . K 机器人一定要走的步数
按着上面这个思路：在每一次移动中，改变的参数事start,剩下可以走的步数，不变的是N ，和end .
关注一下这两个可变参数的范围，确定其取值范围
套路：1.尝试 2.可变参数的组合（分析），表的大小确定 3.给具体参数的例子 4. 在表中最终想要的位置（看主函数怎么调用）5.最简单位置填好（base case） 6.分析普遍位置依赖（看尝试方法）
CD17机器人达到指定位置方法数
只能走到2位置，如果机器人在N位置，那么下一步机器人只能走到N-1位置。规定机器人只能走k步，最终能来到P位置的方法有多少种。由于方案数可能比较大，所以答案需要对1e9+7取模。
输入描述：
输出包括一行四个正整数N（2<=N<=5000）、M(1<=M<=N)、K(1<=K<=5000)、P(1<=P<=N)。
输出描述：
输出一个整数，代表最终走到P的方法数对109+710^9+7109+7取模后的值。

5 2 3 3
输出：

3
说明：
1).2->1,1->2,2->3

2).2->3,3->2,2->3

3).2->3,3->4,4->3
输入：

1000 1 1000 1
输出：
591137401
说明：
注意答案要取模
备注：
时间复杂度O(n∗k)O(n*k)O(n∗k),空间复杂度O(N)O(N)O(N)。

思路：确定状态的方法1.思考最后一个状态是什么 ？可以拆分什么子结构 2.观察一下整个过程中那些参数是可变参数（一般1-2个），由此可以知道状态如何转移，使思路更加清晰。
由这可变参数确定dp表的大小，先用示例自己推演一下，接下来就是写代码的过程了




1
2
3
4
5




0
0
1
0
0
0


1
1
0
1
0
0


2
0
2
0
1
0


3
2
0
@(2+1)
0
1



@处就是表示我们要求的位置的，以上就是示例一的推演过程，不难理解
#include 
#define P 1000000007

using namespace std;

int main(){
    int n,m,k,p;
    cin>>n>>m>>k>>p;
    vector dp;
    //初始化base case
    for(int i = 0;i temp(dp);
        for(int j = 0;jO(n)

64. 最小路径和
class Solution {
public:
    int minPathSum(vector>& grid) {
        int dp[grid.size()][grid[0].size()];
        //初始化
        dp[0][0] = grid[0][0];
        for(int i =1;idp[i][j-1]?dp[i][j-1]:dp[i-1][j];
                dp[i][j] = grid[i][j] + temp;
            }
        }
        //返回
        return dp[grid.size()-1][grid[0].size()-1];
    }
};
//2021.6.7动态规划

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VybTSMmw-1631787002281)(C:\Users\1\Desktop\微信图片_20210607120234.png)]

求路径
class Solution {
public:
    /**
     * 
     * @param m int整型 
     * @param n int整型 
     * @return int整型
     */
    int uniquePaths(int m, int n) {
        // write code here
        int dp[m][n];
        //初始化base case
        for(int i = 0;i

63. 不同路径 II
class Solution {
public:
    int uniquePathsWithObstacles(vector>& obstacleGrid) {
        if(obstacleGrid[0][0] ==1 || obstacleGrid[obstacleGrid.size()-1][obstacleGrid[0].size()-1] ==1)return 0;
        //确定状态，明确选择
        int dp[obstacleGrid[0].size()];
        //初始化base case
        dp[0] = 1;
        for(int i = 1;i

剑指 Offer 47. 礼物的最大价值
class Solution {
public:
    int maxValue(vector>& grid) {
        int dp[grid[0].size()];
        //初始化base case
        dp[0] = grid[0][0];
        for(int i = 1;i

样本问题
53. 最大子序和
class Solution {
public:
    int maxSubArray(vector& nums) {
        if(nums.size() == 1)return nums[0];
        
        int dp[nums.size()];
        //初始化base case
        dp[0] = nums[0];
        int max = dp[0];
        //状态转移
        for(int i = 1;i=0){
                dp[i] = (nums[i]+dp[i-1])>0?(nums[i]+dp[i-1]):0;
            }else{
                dp[i] = nums[i];
            }
            max = dp[i]>max?dp[i]:max;
        }
        //返回
        return max;
    }
};

dp规划问题，有些是返回dp最后一个元素，或者要查询的元素。像上面这道题，就是返回这个dp数组的最大值
所以解题的思路是，确立base case ,初始化base case。然后根据题意，确定如何生成这个dp数组，其实就是确定如何状态转移方程（状态转移方程可能是有多个的）。最后返回这个dp数组中你要的数据，即答案即可。
背包问题
剑指 Offer 46. 把数字翻译成字符串
给定一个数字，我们按照如下规则把它翻译为字符串：0 翻译成 “a” ，1 翻译成 “b”，……，11 翻译成 “l”，……，25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数，用来计算一个数字有多少种不同的翻译方法。

示例 1:
输入: 12258
输出: 5
解释: 12258有5种不同的翻译，分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"

class Solution {
public:
    int translateNum(int num) {
        string str(std::to_string(num));
        if(num ==0)return 1;

        int dp[str.size()+1];
        //初始化base case
        dp[0] = 1;
        dp[1] = 1;
        int temp = 0;
        //状态转移
        for(int i = 2; i <= str.size(); i++){
            temp = (str[i-2]-'0')*10+(str[i-1]-'0');
            if(temp<=25 && temp>=10){
                dp[i] = dp[i-1]+dp[i-2];
            }else{
                dp[i] = dp[i-1];
            }
        }
        //返回答案
        return dp[str.size()];
    }
};
//2021.6.9 动态规划

把数字翻译成字符串(二)
描述
有一种将字母编码成数字的方式：'a'->1, 'b->2', ... , 'z->26'。
现在给一串数字，返回有多少种可能的译码结果
示例1
输入：

"12"
返回值：2
说明：
2种可能的译码结果（”ab” 或”l”）
示例2
输入："31717126241541717"
返回值：192
说明：192种可能的译码结果

class Solution {
public:
    /**
     * 解码
     * @param nums string字符串 数字串
     * @return int整型
     */
    int solve(string nums) {
        // write code here
        //去除无效数据
        if(nums[0] == '0')return 0;
        int dp[nums.size()+1];
        //初始化base case
        dp[0] = 1;
        dp[1] = 1;
        //状态转移
        int temp = 0;
        for(int i = 2;i<=nums.size();i++){
            temp = (nums[i-2]-'0')*10+(nums[i-1]-'0');
            if(temp<=26){
                if(nums[i-2] == '0')dp[i] = dp[i-1];
                else
                    dp[i] = dp[i-2]+dp[i-1];
                if(nums[i-1]=='0'){
                    dp[i] = dp[i-2];
                    dp[i-1] = dp[i-2];
                }
                if(temp == 0)return 0;
            }else{
                if(nums[i-1]=='0')return 0;
                dp[i] = dp[i-1];
            }
        }
        //返回答案
        return dp[nums.size()];
    }
};
//时间复杂度是On,空间复杂度是On,空间上可以优化为O1，但是时间复杂度On的系数会发生改变，变大。在较小样本上，时间复杂度发生的改变会体现的比较明显

上面这两道题其实很显示，但是一道是‘a’->1,一道是’a’->0,由此在状态转移那有很多特殊的例子要考虑到，一定要手写示意图，好好理解特殊例子的处理。比如第二题是出现0 的情况，100，2010，023，3012等情况都要在状态转移方程中好好考虑清楚。总而言之，上面这两道题状态转移方程大致是一样，不同的地方是在于特殊位置的处理，稍有不同。
换钱的最少货币数
描述
给定数组arr，arr中所有的值都为正整数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张，再给定一个aim，代表要找的钱数，求组成aim的最少货币数。
如果无解，请返回-1.
【要求】
时间复杂度O(n×aim)O(n \times aim)O(n×aim)，空间复杂度On。


class Solution {
public:
    /**
     * 最少货币数
     * @param arr int整型vector the array
     * @param aim int整型 the target
     * @return int整型
     */
    int minMoney(vector& arr, int aim) {
        int max = aim+1;
        int dp[aim+1];
        //初始化base case 
        dp[0] = 0;
        for(int i = 1;i<=aim;i++){
            dp[i] = max;
        }
        //状态转移
        for(int i =1;i<=aim;i++){
            for(int j = 0;j=0){
                    dp[i] = min(dp[i],dp[i-arr[j]]+1);
                }
            }
        }
        //return;
        return (dp[aim]!=max)?dp[aim]:-1;
    }
};

//解法二
#include 

using namespace std;

int main(){
    int n;
    int aim;
    cin>>n>>aim;
    vector choose;
    for(int i = 0;i>temp;
        choose.emplace_back(temp);
    }
    const int zhi = aim+1;
    int dp[zhi];
    //初始化base case
    dp[0] = 0;
    for(int i = 1;i<=aim;i++){
        dp[i] = (i%choose[0])==0?i/choose[0]:-1;
    }
    //状态 转移
    for(int i = 1;i=choose[i]){
                if(dp[j]!=-1)
                    dp[j] = (dp[j-choose[i]]!=-1)?min(dp[j],1+dp[j-choose[i]]):dp[j];
                else
                    dp[j] = (dp[j-choose[i]]!=-1)?max(dp[j],1+dp[j-choose[i]]):dp[j];
            }
        }
    }
    //return
    cout<

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-53VJFXiZ-1631787002284)(C:\Users\1\AppData\Local\Temp\WeChat Files\d492143173622e74c83abecc47ee259.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FPDy6pun-1631787002285)(C:\Users\1\AppData\Local\Temp\WeChat Files\42687ef31d1363e9e12a3d5142b0cc6.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jVmd9HeX-1631787002285)(C:\Users\1\AppData\Local\Temp\WeChat Files\50d07a5b01ac1c1592d460f31a7a8c8.png)]

01背包问题
物品顺序是固定
推出重叠子问题，那么从最基础的base case 开始就是一步一步由子结构推算到最终答案
描述
已知一个背包最多能容纳物体的体积为V
现有n个物品第i个物品的体积为viv_ivi 第i个物品的重量为wiw_iwi
求当前背包最多能装多大重量的物品

示例1
输入：
10,2,[[1,3],[10,4]]
返回值：
4
说明：
第一个物品的体积为1，重量为3，第二个物品的体积为10，重量为4。只取第二个物品可以达到最优方案，取物重量为4 

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 计算01背包问题的结果
     * @param V int整型 背包的体积
     * @param n int整型 物品的个数
     * @param vw int整型vector> 第一维度为n,第二维度为2的二维数组,vw[i][0],vw[i][1]分别描述i+1个物品的vi,wi
     * @return int整型
     */
    int knapsack(int V, int n, vector >& vw) {
        int dp[n+1][V+1];
        //初始化base case
        for(int i = 0;i<=V;i++){
            dp[0][i] = 0;
        }
        for(int i = 0;i<=n;i++){
            dp[i][0] = 0;
        }
        //状态转移  dp[i][j] = max{dp[i-1][j],dp[j-]}
        for(int i = 1;i<=n;i++){
            for(int j = 1;j<=V;j++){
                if(j>=vw[i-1][0]){
                    dp[i][j] = max(dp[i-1][j],vw[i-1][1]+dp[i-1][j-(vw[i-1][0])]);
                }else{
                    dp[i][j] = dp[i-1][j];
                }
            }
        }
        //返回
        return dp[n][V];
    }
};

279. 完全平方数
class Solution {
public:
    int numSquares(int n) {
        //明确状态与选择
        int dp[n+1];
        //初始化base case
        for(int i = 0;i<=n;i++){
            dp[i] = i; 
        }
        //状态转移
        int zhi = 2;
        while((zhi*zhi)<=n)
        {
            for(int i = 0;i<=n;i++){
                if(i>=(zhi*zhi)){
                    dp[i] = min(dp[i],1+dp[i-(zhi*zhi)]);
                }
            }
            zhi++;
        }
        //return
        return dp[n];

    }
};

这段题是01背包的思想，迁移一下就会了
股票问题
121. 买卖股票的最佳时机
class Solution {
public:
    int maxProfit(vector& prices) {
        //确定状态，明确选择
        int dp[prices.size()][3];
        //base case
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        dp[0][2] = 0;
        for(int i = 1;i

上面这道题可以优化至空间复杂度为O1。
123. 买卖股票的最佳时机 III
class Solution {
public:
    int maxProfit(vector& prices) {
        //确定状态，明确选择
        int dp[5];
        //初始化base case
        dp[0] = 0;           //不操作
        dp[1] = -prices[0];  //第一次买入
        dp[2] = 0;           //第一次卖出
        dp[3] = -prices[0];  //第二次买入
        dp[4] = 0;           //第二次卖出
        //状态转移
        for(int i = 1;i

演练一下dp表格，在做空间复杂度上的优化，时间复杂度On
188. 买卖股票的最佳时机 IV
class Solution {
public:
    int maxProfit(int k, vector& prices) {
        //确定状态，明确选择
        int dp[2*k+1];
        if(prices.size() == 0)return 0;
        //初始化base case
        for(int i = 0;i<(2*k+1);i++){
            if(i%2 == 0){
                dp[i] = 0;
            }else{
                dp[i] = -prices[0];
            }
        }
        //状态转移
        for(int i = 1;i

关于股票问题的几道题，原理很相似，知道第一的解法，便可以触类旁通
392. 判断子序列
给定字符串 s 和 t ，判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。
输入：s = "abc", t = "ahbgdc"
输出：true
输入：s = "axc", t = "ahbgdc"
输出：false

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int len_s = s.size();
        int len_t = t.size();
        //洗除无效数据
        if(len_s == 0)return true;
        if(len_t == 0)return false;
        //明确状态和选择
        bool dp[len_s+1][len_t+1];   //一定要想好这里的每一个元素代表的意义
        //初始化base case
        for(int i = 0;i<=len_t;i++)
        {
            dp[0][i] = true;
        }
        for(int i = 1;i<=len_s;i++)
        {
            dp[i][0] = false;
        }
        //状态转移
        for(int i = 1;i<=len_s;i++)
        {
            for(int j = 1;j<=len_t;j++)
            {
                dp[i][j] = ((dp[i][j-1])||((s[i-1] == t[j-1]) && dp[i-1][j-1]))?true:false;
            }
        }
        //返回结果
        return dp[len_s][len_t];
    }
};

找出可以参数，确定dp表格，明确状态与选择是要明白这个表格每一格代表的意思，理解好（这一步对状态转移方程的确定很重要）
打家劫舍系列
分类线性动态规划–单串
198. 打家劫舍
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。


0.判断是否为动态规划的题型：最后一个状态原则，即f(n)是否可以拆成其他子状态，且无后效性
1.可变参数是，[0-n],代表的是0到n子数组 ，n<数组的长度
2.明确状态：dp[i] 的实际意义 比如这里的意义是代表 子数组从0-i处的最优选择
3.确定选择：选择即是状态有由哪些状态转换而来，根据实际确定有哪些选择
（1）偷窃第 kkk 间房屋，那么就不能偷窃第 k-1 间房屋，偷窃总金额为前 k-2间房屋的最高总金额与第 k 间房屋的金额之和。
（2）不偷窃第 k 间房屋，偷窃总金额为前 k-1 间房屋的最高总金额。
这是选择，这道题是求最优，那就要在两个选择之间选择最优，因为这两个选择是互不影响的，也不是累加起来到达下一下状态，
dp[i]=max(dp[i−2]+nums[i],dp[i−1]) 这就是状态转移方程；
4.确定base case 根据实际，确定，dp[0] dp[1] 两个状态的初始值，因为值两个值，可以人为确定，且无法有子状态转移过来
5.确定返回值。根据状态的实际意义，确定在表格中，我们要返回的位置
class Solution {
public:
    int rob(vector& nums) {
        const int len  = nums.size();
        if (len == 1) return nums[0];
        if (len == 2) return max(nums[0],nums[1]);
        int dp[len];   //代表带n家处，最多金额数  //这一步是明确状态，就是要明白状态代表什么意思
        //初始化base case
        dp[0] = nums[0];
        dp[1] = max(nums[0],nums[1]);                    //状态最开始的情况
        //状态转移方程 f() = max(nums[i]+f(i-2),f(i-1));
        for (int i=2; i

213. 打家劫舍 II
你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。
输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

输入：nums = [1,2,3,1]
输出：4
解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
     偷窃到的最高金额 = 1 + 3 = 4 。

思路：这道题在前面那道题理解的情况下就很好做，做这种题要理解好状态代表的实际意思。
根据题意，理解，这道题其实就是头元素和尾元素，不能同时取得，其他元素的做法其实就是第一道题的思路。
所以就是考虑没有头元素是的最优解，和没有尾元素的最优解，两者比较得到答案
class Solution {
public:
    int rob(vector& nums) {
        const int len = nums.size();
        if (len == 1) return nums[0];
        if (len == 2) return max(nums[0],nums[1]);
        if (len == 3) return max(nums[0],max(nums[1],nums[2]));
        int dp[len-1];
        dp[0] = nums[0];
        dp[1] = max(nums[0],nums[1]);

        for (int i = 2;i my(nums.begin()+1,nums.end());
        dp2[0] = my[0];
        dp2[1] = max(my[0],my[1]);
        
        for (int i = 2;i

740. 删除并获得点数
给你一个整数数组 nums ，你可以对它进行一些操作。

每次操作中，选择任意一个 nums[i] ，删除它并获得 nums[i] 的点数。之后，你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。

开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。

输入：nums = [3,4,2]
输出：6
解释：
删除 4 获得 4 个点数，因此 3 也被删除。
之后，删除 2 获得 2 个点数。总共获得 6 个点数。

输入：nums = [2,2,3,3,3,4]
输出：9
解释：
删除 3 获得 3 个点数，接着要删除两个 2 和 4 。
之后，再次删除 3 获得 3 个点数，再次删除 3 获得 3 个点数。
总共获得 9 个点数。



struct node{
    int val;
    int nums;
    node(int a,int b):val(a),nums(b){};
};
class Solution {
public:
    int deleteAndEarn(vector& nums) {
        unordered_map hstable;
        //先统计值，及其总量
        for (int i = 0;isecond+=nums[i];
            }
        }
        vector vec;
        //保存并排序
        for (auto i:hstable)
        {
            vec.emplace_back(node(i.first,i.second));
        }
        sort(vec.begin(),vec.end(),[=](node &a,node &b)->bool{
            return a.val

这道题也是打家劫舍的一道经典的题，做题时要根据题意，将题意转换成比较容易处理的样子。这是一种技巧，也需要多刷题才能培养出这种感觉。
先将相同值的元素统一起来，之后在是排序，排序的顺序的好处在于将小于1和大于1，转化成只需要考虑大于1的情况。
后续的处理就是打家劫舍1的思路了
串的问题
5. 最长回文子串
给你一个字符串 s，找到 s 中最长的回文子串。
输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

输入：s = "cbbd"
输出："bb"

这是一道很重要的题目，也很经典
dp【i】【j】 表示的状态是字符串i到j 字串是否为回文串
其思想就是盘窜i+1,到j-1之间的子串是否为回文串，然后再比较i 和j 处的字符是否相等
class Solution {
public:
    string longestPalindrome(string s) {
        const int len = s.size();
        bool dp[len][len]; //每个状态是代表在字符串中i  到  j 是否为回文串
        //初始化base case 
        for (int i = 0;i=0;j--)   //行
            {
                if (j == (i-1))
                {
                    dp[j][i] = (s[i] == s[j])?true:false;
                }
                else
                {
                    dp[j][i] = dp[j+1][i-1] && (s[j] == s[i])?true:false;  //状态转移方程
                }
                if (dp[j][i])     //为回文串，则判断一下回文串的大小
                {
                    //std::cout<

队列、栈
队列的特点是先进先出，栈的特点是先进后出。队列的front()是指向要先出来的那个元素，栈的top元素是指向栈顶。
size()是容器的中的元素个数
用两个栈实现队列
class Solution
{
public:
    void push(int node) {
        stack1.push(node);
    }

    int pop() {
        if(stack2.empty()){
            while(!stack1.empty()){
                stack2.push(stack1.top());
                stack1.pop();
            }
        }
        int ans = stack2.top();
        stack2.pop();
        return ans;
    }

private:
    stack stack1;
    stack stack2;
};

设计getMin功能的栈
描述
实现一个特殊功能的栈，在实现栈的基本功能的基础上，再实现返回栈中最小元素的操作。
示例1
输入：

[[1,3],[1,2],[1,1],[3],[2],[3]]

返回值：

[1,2]

备注：

有三种操作种类，op1表示push，op2表示pop，op3表示getMin。你需要返回和op3出现次数一样多的数组，表示每次getMin的答案

1<=操作总数<=1000000
-1000000<=每个操作数<=1000000
数据保证没有不合法的操作

我的做法是用两个数组来模拟 这个栈
其中一个数组用来保存值，一个用于保存存入的最小值（用了单调栈的思想），保存的值是另一个数字的最小值的索引。
在弹出和压入时均要判断最小值是否被弹出
class Solution {
public:
    /**
     * return a array which include all ans for op3
     * @param op int整型vector> operator
     * @return int整型vector
     */
    vector getMinStack(vector >& op) {
        // write code here
        vector ans;
        for(int i = 0;i mystack;
        vector nstack;
};

739. 每日温度
请根据每日 气温 列表，重新生成一个列表。对应位置的输出为：要想观测到更高的气温，至少需要等待的天数。如果气温在这之后都不会升高，请在该位置用 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

这是一道华为面试算法题
单调栈的思想，其实栈栈中存放的是index就行，后续用数组的值去索引就行，这样就可以减少内存资源了。
我下面的做法是用了一个节点结构体，结构体中存放值和索引，比较值，放节点，算是单调栈的思想
struct node{
    int val;
    int index;
    node(int a,int b):val(a),index(b){}
};
class Solution {
public:
    vector dailyTemperatures(vector& t) {
        const int len = t.size();
        vector ans(len,0);
        stack temp;
        for (int i = 0;i=t[i])
                {
                    temp.push(node(t[i],i));
                }else{
                    while (!temp.empty() && temp.top().val

前缀和
题目描述

牛牛拿到了一个长度为  的数组 , 作为一个魔法师，他可以每次选择一个 ，施展一次魔法使  加1或者减1。现在对于每一个  ，牛牛想知道将  中所有的数字变成  最少要施展几次魔法。

函数传入一个数组，你需要返回一个数组，假设数组为，则是将  中所有的数字变成  最少施展魔法的次数。
样例1
输入

[3,1,4,5,3]

返回值

[5,11,6,9,5]


[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Kf5x1zVn-1631787002288)(upload\image-20210625104414403.png)]
struct node{
    int val;
    int index;
    node(int a,int b):val(a),index(b){}
};
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param h int整型vector 
     * @return int整型vector
     */
    vector Magical_NN(vector& h) {
        vector mynode;
        for(int i = 0;ibool{
            return a.val myvec;//前缀和
        myvec.emplace_back(mynode[0].val);
        for(int i = 1;i ans(myvec.size(),0);
        for(int i = 0;i

前缀和就是在建立一个数组，每个数组中i位置保存的值是，数组前i个元素之和
用在那种需要多次求和的情况，是一种编程技巧，用空间替换时间
贪心算法
767. 重构字符串
给定一个字符串S，检查是否能重新排布其中的字母，使得两相邻的字符不同。

若可行，输出任意可行的结果。若不可行，返回空字符串。
输入: S = "aab"
输出: "aba"
输入: S = "aaab"
输出: ""

在重新构建字符串时，用到贪心思想
首先是判断是否需要重构嘛
其次如果需要重构，则用贪心思想去重构
struct node{
    char ch;
    int val;
    node(char a,int b):ch(a),val(b){}
};

struct cmp{
    bool operator () (node &a,node &b)
    {
        return a.val str(26,0);
        for (int i = 0;i,cmp> b_heal;   //大根堆
        for (int i = 0;i<26;i++)
        {
            if(str[i] != 0)
            {
                b_heal.emplace(node('a'+i,str[i]));
            }
        }
        string ans;
        if (s.size()%2 ==0)  //偶数
        {
            if(b_heal.top().val>s.size()/2)
            return ans;
        }else{               //奇数
            if(b_heal.top().val>(s.size()/2+1))
            return ans;
        }
        //重新排序    贪心思想
        while (b_heal.size()>=2)
        {
            node a = b_heal.top();
            b_heal.pop();
            node b = b_heal.top();
            b_heal.pop();
            ans.push_back(a.ch);
            a.val--;
            if (a.val != 0)b_heal.push(a);
            ans.push_back(b.ch);
            b.val--;
            if (b.val != 0) b_heal.push(b);
        }
        if(!b_heal.empty())
            ans.push_back(b_heal.top().ch);
        return ans;
    }
};

图
dijkstra (单源最小路径)
NC158 单源最短路
描述
在一个有向无环图中，已知每条边长，求出1到n的最短路径，返回1到n的最短路径值。如果1无法到n，输出-1 
输入：

5,5,[[1,2,2],[1,4,5],[2,3,3],[3,5,4],[4,5,5]]

返回值：
9
两个整数n和m,表示图的顶点数和边数。
一个二维数组，一维3个数据，表示顶点到另外一个顶点的边长度是多少
每条边的长度范围[0,1000]。
注意数据中可能有重边

class Node;
class Edge;
class Graph;
class Creator;

class Node{
public:
    int value;
    int in;
    int out;
    vector nodes;
    vector edges;
    Node(int a):value(a),in(0),out(0){}
    bool operator <(const Node &a)const
    {
        return value *nodes;
    unordered_map *edges;
    Graph()
    {
        nodes = new unordered_map();
        edges = new unordered_map();
    }
    ~Graph()
    {
        delete nodes;
        delete edges;
    }
};
class Creator{
public:
    Creator(const vector> &vec)
    {
        mygraph = new Graph();
        for (int i = 0;inodes->find(from) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(from,Node(from));
            }
            if (mygraph->nodes->find(to) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(to,Node(to));
            }
            Node *fromNode = &mygraph->nodes->at(from);
            Node *toNode = &mygraph->nodes->at(to);
            Edge newEdge = Edge(weight,fromNode,toNode);
            fromNode->out++;
            toNode->in++;
            fromNode->nodes.emplace_back(*toNode);
            fromNode->edges.emplace_back(newEdge);
            string key = to_string(to);
            key.push_back('-');
            key += to_string(from);
            mygraph->edges->emplace(key,newEdge);
        }
    }
    ~Creator()
    {
        delete mygraph;
    }
    Node getminunuesd(const map &distance,const set &hstable)
    {
        int minval = INT_MAX;
        Node ans = Node(0);
        for (auto i:distance)
        {
            if (hstable.find(i.first) == hstable.end() && i.second dijkstra()
    {
        Node *node = &mygraph->nodes->at(1);
        map distance;
        if (node == nullptr)
        {
            return distance;
        }
        set hstable;
        distance.emplace(*node,0);
        Node minNode = getminunuesd(distance,hstable);
        while (minNode.value != 0)
        {
            int dis = distance[minNode];
            for (Edge i: minNode.edges)
            {
                Node toNode = *i.to;
                if (distance.find(toNode) == distance.end())
                {
                    distance.emplace(toNode,dis+i.weight);
                }else{
                    distance[toNode] = min(distance[toNode],dis+i.weight);
                }
            }
            hstable.emplace(minNode);
            minNode = getminunuesd(distance, hstable);
        }
        return distance;
    }
private:
    Graph *mygraph;
};
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param n int 顶点数
     * @param m int 边数
     * @param graph intvector> 一维3个数据，表示顶点到另外一个顶点的边长度是多少
     * @return int
     */
    int findShortestPath(int n, int m, vector >& graph) {
        // write code here
        Creator zj = Creator(graph);
        map ans = zj.dijkstra();
        if (ans.find(Node(n)) == ans.end())
        {
            return -1;
        }
        return ans[Node(n)];
    }
};

743. 网络延迟时间
有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。
输入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出：2
输入：times = [[1,2,1]], n = 2, k = 1
输出：1
输入：times = [[1,2,1]], n = 2, k = 2
输出：-1

单源最短路径算法，其中最大值就是答案。
class Node;
class Edge;
class Graph;
class Creator;
class Node{
public:
    int value;
    vector *edge = nullptr;
    Node(int a):value(a)
    {
        edge = new vector();
    }
    bool operator<(const Node &a)const
    {
        return value* nodes = nullptr;
    Graph()
    {
        nodes = new unordered_map();
    }
    ~Graph()
    {
        for (auto i:*nodes)
        {
            delete i.second.edge;
        }
        delete nodes;
    }
};
class Creator{
public:
    Creator(const vector>& vec)
    {
        mygraph = new Graph();
        for (int i = 0;inodes->find(from)==mygraph->nodes->end())
            {
                mygraph->nodes->emplace(from,Node(from));
            }
            if (mygraph->nodes->find(to) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(to,Node(to));
            }
            Node* fromNode = &mygraph->nodes->at(from);
            Node* toNode = &mygraph->nodes->at(to);
            Edge newedge = Edge(weight,toNode);
            fromNode->edge->emplace_back(newedge);
        }
    }
    ~Creator()
    {
        delete mygraph;
    }
    //核心
    Node getminunuse(map &distance,set &hstable)
    {
        int maxval = INT_MAX;
        Node ans = Node(0);
        for (auto i:distance)
        {
            if (hstable.find(i.first) == hstable.end() && i.second distance;
        set hstable;
        Node temp = mygraph->nodes->at(k);
        distance.emplace(temp,0); //自己到自己为0；
        Node node = getminunuse(distance,hstable);
        while (node.value !=0)
        {
            int dis = distance[node];
            for (Edge i:*node.edge)
            {
                if (distance.find(*i.toNode) == distance.end())
                {
                    distance.emplace(*i.toNode,i.weight+dis);
                }else{
                    distance[*i.toNode] = min(distance[*i.toNode],i.weight+dis);
                }
            }
            hstable.emplace(node);
            node = getminunuse(distance,hstable);
        }
        if(distance.size() != n)return -1;
        int ans = 0;
        for (auto i:distance)
        {
            ans = max(i.second,ans);
        }
        return ans;
    }
private:
    Graph* mygraph;
};
class Solution {
public:
    int networkDelayTime(vector>& times, int n, int k) {
        Creator zj = Creator(times);
        return zj.dijkstra(n,k);
    }
};

深度优先
树的前、中、后都是深度优先遍历。后序遍历的思想在解读一些树的问题中非常有用，需要在做题的过程中不断总结和体会
。深度优先遍历 只要前面有可以走的路，就会一直向前走，直到无路可走才会回头；
「无路可走」有两种情况：① 遇到了墙；② 遇到了已经走过的路；
在「无路可走」的时候，沿着原路返回，直到回到了还有未走过的路的路口，尝试继续走没有走过的路径；
有一些路径没有走到，这是因为找到了出口，程序就停止了；
「深度优先遍历」也叫「深度优先搜索」，遍历是行为的描述，搜索是目的（用途）；
遍历不是很深奥的事情，把 所有 可能的情况都看一遍，才能说「找到了目标元素」或者「没找到目标元素」。遍历也称为 穷举，穷举的思想在人类看来虽然很不起眼，但借助 计算机强大的计算能力，穷举可以帮助我们解决很多专业领域知识不能解决的问题
129. 求根节点到叶节点数字之和
给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumNumbers(TreeNode* root) {
        int ans = 0;
        int num = 0;
        proess(root,num,ans);
        return ans;
    }
    void proess(TreeNode* head,int &num,int& ans)
    {
        if (head == nullptr)return ; 
        num*=10;
        num+=head->val;
        proess(head->left,num,ans);
        proess(head->right,num,ans);
        if(head->left == nullptr && head->right == nullptr)ans+=num;
        num-=head->val;
        num/=10;
    }
};

广度优先
863. 二叉树中所有距离为 K 的结点
给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 K 。

返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。
输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
输出：[7,4,1]
解释：
所求结点为与目标结点（值为 5）距离为 2 的结点，
值分别为 7，4，以及 1

注意，输入的 "root" 和 "target" 实际上是树上的结点。
上面的输入仅仅是对这些对象进行了序列化描述。


1.先遍历树，用层序遍历
2.建图
3.图的层序遍历
4.注意特殊例子
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Node;
class Graph;
class Creator;
class Node{
public:
    int value;
    vector* next = nullptr;
    Node(int v):value(v)
    {
        next = new vector();
    }
    bool operator<(const Node& a)const
    {
        return value* nodes = nullptr;
    Graph()
    {
        nodes = new unordered_map();
    }
    ~Graph()
    {
        for (auto i:*nodes)
        {
            delete i.second.next;
        }
        delete nodes;
    }
};
class Creator{
public:
    Creator(const vector>& vec)
    {
        mygraph = new Graph();
        for (int i = 0;inodes->find(from) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(from,Node(from));
            }
            if (mygraph->nodes->find(to) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(to,Node(to));
            }
            Node* fromNode = &mygraph->nodes->at(from);
            Node* toNode =  &mygraph->nodes->at(to);
            fromNode->next->emplace_back(*toNode);
            toNode->next->emplace_back(*fromNode);
        }
    }
    ~Creator()
    {
        delete mygraph;
    }
    vector bfs(int target,int K)
    {
        Node temp = mygraph->nodes->at(target);
        queue myqueue;
        set hstable;
        myqueue.push(temp);
        hstable.emplace(temp);
        vector ans;
        int cen = 0;
        while (!myqueue.empty())
        { 
            int n = myqueue.size();
            for (int i = 0;i distanceK(TreeNode* root, TreeNode* target, int k) {
        if (root->left == nullptr && root->right == nullptr) return vector();  //左右节点为空的情况
        int mytarget = target->val;
        vector ans;
        ans.emplace_back(mytarget);
        if(k == 0)return ans;    //注意特殊例子要优先考虑  等于0 的情况
        vector> vec;
        proess(root,vec);
        
        Creator zj = Creator(vec);   //建图
        return zj.bfs(mytarget,k);   
        /*for (auto i:vec)
        {
            cout<();*/
    }
    void proess(TreeNode* head,vector>& vec)  //层序遍历
    {
       //层序遍历
       vector temp;
       queue myqueue;
       myqueue.push(head);
       TreeNode* mid = nullptr;
       while (!myqueue.empty())
       {
           mid = myqueue.front();
           myqueue.pop();
           temp.emplace_back(mid->val);
           if (mid->left != nullptr)
           {
               myqueue.push(mid->left);
               temp.emplace_back(mid->left->val);
               vec.emplace_back(temp);
               temp.pop_back();
           }
           if (mid->right != nullptr)
           {
               myqueue.push(mid->right);
               temp.emplace_back(mid->right->val);
               vec.emplace_back(temp);
               temp.clear();
           }else{
               temp.clear();
           }
       }
    }
};

拓扑排序
做了leetcode中的课程表，我晕了，，，手贱，把顶点结构中的vector 这个成员我定义成变量，导致在初始化生成图时，不断的拷贝值，导致占用大量时间，整个建图的过程，2000个顶点的图耗时700ms,每次运行代码都会报错时间超时了。后发现将vector 变量定义成指针变量，之后再之后的emplace_back时，更为高效，耗时4ms.
207. 课程表
你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程  bi 。
    例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。
输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。


class Node;
class Graph;
class Creator;
class Node{
public:
    int value;
    int in;
    vector *nexts = nullptr;   
    Node(int a):value(a),in(0){
        nexts = new vector();
    }
    bool operator <(const Node &a)const
    {
        return value *nodes;
    Graph()
    {
        nodes = new unordered_map();
    }
    ~Graph()
    {
        for (auto i:*nodes)   //释放内存
        {
            delete i.second.nexts;
        }
        delete nodes;
    }
};

class Creator{
public:
    Creator(const vector> &vec)   //生成图  只保留对题目有用的图信息
    {
        mygraph = new Graph();
        for (int i = 0;inodes->find(from) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(from,Node(from));
            }
            if (mygraph->nodes->find(to) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(to,Node(to));
            }
            Node *fromNode = &mygraph->nodes->at(from);
            Node *toNode  = &mygraph->nodes->at(to);
            toNode->in++;
            fromNode->nexts->emplace_back(*toNode);  //
        }
    }
    //核心
    bool tpsort()
    {
        queue myqueue;    ///队列保存入度为零的点
        set hstable;
        for (auto i: *mygraph->nodes)
        {
            hstable.emplace(i.second);
            if (i.second.in == 0)
            {
                hstable.erase(hstable.find(i.second));
                myqueue.push(i.second);
            }
        }
        //std::cout<in == 0)
                    {
                        myqueue.push(*hstable.find(i));
                        hstable.erase(hstable.find(i)); 
                        
                    }
                }
        }
       // std::cout<>& prerequisites) {
        if (prerequisites.size() == 0)return true;    //清除无效数据
        Creator zj = Creator(prerequisites);
        return zj.tpsort();
    }
};

210. 课程表 II
现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。

可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。
输入: 2, [[1,0]] 
输出: [0,1]
解释: 总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

输入: 4, [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
     因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。


class Node;
class Graph;
class Creator;
class Node{
public:
    int value;
    int in;   //入度
    vector *nexts = nullptr;
    Node(int a):value(a),in(0)
    {
        nexts = new vector();
    }
    bool operator <(const Node &a)const
    {
        return value *nodes;  //点集
    Graph()
    {
        nodes = new unordered_map();
    }
    ~Graph()
    {
        for (auto i:*nodes)
        {
            delete i.second.nexts;
        }
        delete nodes;
    }
};
class Creator{
public:
    Creator(const vector> &vec)
    {
        mygraph = new Graph();
        for (int i = 0;inodes->find(from) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(from,Node(from));
            }
            if (mygraph->nodes->find(to) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(to,Node(to));
            }
            Node* fromNode = &mygraph->nodes->at(from);
            Node* toNode = &mygraph->nodes->at(to);
            toNode->in++;
            fromNode->nexts->emplace_back(*toNode);
        }
    }
    ~Creator()
    {
        delete mygraph;
    }
    vector tpsort(const int &nums)
    {
        vector ans;
        //实际需要  没有依赖关系的课程可以先学或者后学都可以
        for (int i = 0;inodes->find(i) == mygraph->nodes->end())
            {
                ans.emplace_back(i);
            }
        }
        queue myqueue;
        set hstable;
        for (auto i:*mygraph->nodes)
        {
            hstable.emplace(i.second);
            if (i.second.in == 0)
            {
                myqueue.push(i.second);
                ans.emplace_back(i.second.value);
                hstable.erase(hstable.find(i.second));
            }
        }
        while (!myqueue.empty())
        {
            Node temp = myqueue.front();
            myqueue.pop();
            for (Node i:*temp.nexts)
            {
                Node node = *hstable.find(i);
                hstable.erase(hstable.find(i));
                node.in--;
                hstable.emplace(node);
                if (node.in == 0)
                {
                    myqueue.push(node);
                    ans.emplace_back(node.value);
                    hstable.erase(hstable.find(node));
                }
            }
        }
        if (!hstable.empty())return vector{};
        return ans;
    }
private:
    Graph *mygraph;
};
class Solution {
public:
    vector findOrder(int numCourses, vector>& prerequisites) {
        Creator zj = Creator(prerequisites);
        return zj.tpsort(numCourses);
    }
};

851. 喧闹和富有
在一组 N 个人（编号为 0, 1, 2, ..., N-1）中，每个人都有不同数目的钱，以及不同程度的安静（quietness）。

为了方便起见，我们将编号为 x 的人简称为 "person x "。

如果能够肯定 person x 比 person y 更有钱的话，我们会说 richer[i] = [x, y] 。注意 richer 可能只是有效观察的一个子集。

另外，如果 person x 的安静程度为 q ，我们会说 quiet[x] = q 。

现在，返回答案 answer ，其中 answer[x] = y 的前提是，在所有拥有的钱不少于 person x 的人中，person y 是最安静的人（也就是安静值 quiet[y] 最小的人）。
输入：richer = [[1,0],[2,1],[3,1],[3,7],[4,3],[5,3],[6,3]], quiet = [3,2,5,4,6,1,7,0]
输出：[5,5,2,5,4,5,6,7]
解释： 
answer[0] = 5，
person 5 比 person 3 有更多的钱，person 3 比 person 1 有更多的钱，person 1 比 person 0 有更多的钱。
唯一较为安静（有较低的安静值 quiet[x]）的人是 person 7，
但是目前还不清楚他是否比 person 0 更有钱。

answer[7] = 7，
在所有拥有的钱肯定不少于 person 7 的人中(这可能包括 person 3，4，5，6 以及 7)，
最安静(有较低安静值 quiet[x])的人是 person 7。

其他的答案也可以用类似的推理来解释。


有两个前提条件，一是比当前点富有，二是安静度最小，
第一个条件，用图表示，富有的指向穷的。然后拓扑排序，来比较安静度，拓扑排序就是在用富有的安静度和穷的安静度做比较。
最终的答案是要求返回满足两个条件的点的索引值。
答案数组中初始答案就是本身的点的索引，应该如果没有比它富有的点，那么就不管安静度了，只有它本身了。
用拓扑排序的思想，入度为0的就是富有的，入度为0的点就是表示当前最富有。富有的下一个点就开始比较安静值
比较的思想用符合第一个条件的的点与下一个点的安静度做比较，符合条件就更新答案数组，ans数组里面就是存放着符合条件的点的索引，所以每次比较就用答案数组的值（当前点的最佳索引）所指向的安静度做比较，符合条件就，更新ans数组中的索引。以此类推
class Node;
class Graph;
class Creator;
class Node{
public:
    int index;
    int in;
    vector *nexts = nullptr;
    Node(int a):index(a),in(0)
    {
        nexts = new vector();
    }
    bool operator <(const Node &a)const
    {
        return index *nodes = nullptr;
    Graph()
    {
        nodes = new unordered_map();
    }
    ~Graph()
    {
        for (auto i:*nodes)
        {
            delete i.second.nexts;
        }
        delete nodes;
    }
};
class Creator{
public:
    Creator(const vector> &vec)
    {
        mygraph = new Graph();
        for (int i = 0;inodes->find(from) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(from,Node(from));
            }
            if (mygraph->nodes->find(to) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(to,Node(to));
            }
            Node *fromNode = &mygraph->nodes->at(from);
            Node *toNode = &mygraph->nodes->at(to);
            toNode->in++;
            fromNode->nexts->emplace_back(*toNode);
        }
    }
    vector tpsort(const vector &vec)
    {
        vector ans;
        for (int i = 0;i myqueue;
        set hstable;
        for (auto i:*mygraph->nodes)
        {
            if (i.second.in == 0)
            {
                myqueue.push(i.second);
            }else{
                hstable.emplace(i.second);
            }
        }
        while (!myqueue.empty())
        {
            Node temp = myqueue.front();
            myqueue.pop();
            for (Node i:*temp.nexts)
            {
                if (vec[ans[temp.index]] loudAndRich(vector>& richer, vector& quiet) {
        Creator zj = Creator(richer);
        return zj.tpsort(quiet);
    }
};

最小生成树p 算法
描述
一个有n户人家的村庄，有m条路连接着。村里现在要修路，每条路都有一个代价，现在请你帮忙计算下，最少需要花费多少的代价，就能让这n户人家连接起来。
输入：
3,3,[[1,3,3],[1,2,1],[2,3,1]]
返回值：
2

尽量根据实际情况舍弃一些多余的结构，比如顶点，边，图数据类型，只保存对实际情况有用的数据，使空间复杂度尽可能的小。
class Node;
class Edge;
class Graph;
class Creator;
 
class Node{
public:
    int value;
    /*int in ;
    int out;*/
    //vector nodes;
    vector edges;
    Node(int a):value(a){}
    bool operator <(const Node &a) const
    {
        return valueb.weight;
    }
};
class Graph{
public:
    unordered_map *nodes;
    //unordered_map *edges;
    Graph()
    {
        nodes = new unordered_map();
        //edges = new unordered_map();
    }
    ~Graph()
    {
        delete nodes;
        //delete edges;
    }
};
 
class Creator{
public:
    Creator(const vector> &vec)
    {
        mygraph = new Graph();
        for (int i = 0;inodes->find(from) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(from,Node(from));
            }
            if (mygraph->nodes->find(to) == mygraph->nodes->end())
            {
                mygraph->nodes->emplace(to,Node(to));
            }
            Node *fromNode = &mygraph->nodes->at(from);
            Node *toNode = &mygraph->nodes->at(to);
            Edge newEdge = Edge(weight,toNode);
            /*fromNode->out++;
            toNode->in++;*/
            //fromNode->nodes.emplace_back(*toNode);
            fromNode->edges.emplace_back(newEdge);
            /*string key = to_string(from);
            key.push_back('-');
            key += to_string(to);*/
            //mygraph->edges->emplace(key,newEdge);
        }
    }
    int ptree()
    {
        int ans = 0;
        priority_queue,cmp> s_heal;
        set hstable;
        for (auto i:*mygraph->nodes)
        {
            Node &node = i.second;
            hstable.emplace(node);  //一个点解锁一堆边
            for (Edge j:node.edges)
            {
                s_heal.emplace(j);
            }
            while (!s_heal.empty())
            {
                Edge minedge = s_heal.top();
                s_heal.pop();
                Node &minnode = *minedge.toNode;
                if (hstable.find(minnode) == hstable.end())
                {
                    hstable.emplace(minnode);
                    //ans.emplace_back(minedge);
                    ans+=minedge.weight;
                    for (Edge j:minnode.edges) //解锁一票边
                    {
                        s_heal.emplace(j);
                    }
                }
            }
            break;
        }
        return ans;
    }
    ~Creator()
    {
        delete mygraph;
    }
private:
    Graph *mygraph;
};
 
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 返回最小的花费代价使得这n户人家连接起来
     * @param n int n户人家的村庄
     * @param m int m条路
     * @param cost intvector> 一维3个参数，表示连接1个村庄到另外1个村庄的花费的代价
     * @return int
     */
    int miniSpanningTree(int n, int m, vector >& cost) {
       
        for (int i = 0;i{cost[i][1],cost[i][0],cost[i][2]});
        }
        Creator zj = Creator(cost);
        return zj.ptree();
    }
};

1168. 水资源分配优化
村里面一共有 n 栋房子。我们希望通过建造水井和铺设管道来为所有房子供水。

对于每个房子 i，我们有两种可选的供水方案：

    一种是直接在房子内建造水井，成本为 wells[i]；
    另一种是从另一口井铺设管道引水，数组 pipes 给出了在房子间铺设管道的成本，其中每个 pipes[i] = [house1, house2, cost] 代表用管道将 house1 和 house2 连接在一起的成本。当然，连接是双向的。

请你帮忙计算为所有房子都供水的最低总成本。
输入：n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
输出：3
解释： 
上图展示了铺设管道连接房屋的成本。
最好的策略是在第一个房子里建造水井（成本为 1），然后将其他房子铺设管道连起来（成本为 2），所以总成本为 3。


最小生成树，树形结构，可以借用技巧，加辅助点，就像这道一样，将wells[i]转换成连向一个特殊点的权重，这样就转换成求最小生成树的问题，不然的话，还要考虑还要考虑要用那个水井，如果建一个水井的成本比连通的成本还要低的情况，就会变得很复杂。学习这种灵活转变的思想。一种技巧
class Node;
class Edge;
class Graph;
class Creator;
class Node{
public:
    int value;
    vector *edges = nullptr;
    Node(int a):value(a){
        edges = new vector();
    }
    bool operator <(const Node& a)const
    {
        return valueb.weight;
    }
};
class Graph{
public:
    unordered_map *nodes = nullptr;
    Graph()
    {
        nodes = new unordered_map();
    }
    ~Graph()
    {
        for (auto i:*nodes)
        {
            delete i.second.edges;
        }
        delete nodes;
    }
};
class Creator{
public:
    Creator(const vector& wells,const vector>& pipes)
    {
        mygraph = new Graph();
        mygraph->nodes->emplace(-1,Node(-1));  //水库,这个思想最重要
        for (int i = 0;inodes->emplace(to,Node(to));
            Node* fromNode = &mygraph->nodes->at(from);
            Node* toNode = &mygraph->nodes->at(to);
            fromNode->edges->emplace_back(move(Edge(weight,fromNode,toNode)));
            toNode->edges->emplace_back(move(Edge(weight,toNode,fromNode)));
        }
        for (int i = 0;inodes->at(from);
            Node* toNode = &mygraph->nodes->at(to);
            fromNode->edges->emplace_back(move(Edge(weight,fromNode,toNode)));
            toNode->edges->emplace_back(move(Edge(weight,toNode,fromNode)));
        }
    }
    ~Creator()
    {
        delete mygraph;
    }
    int pmintree()
    {
        priority_queue,cmp> s_heal;
        set hstable;
        for (Edge i:*mygraph->nodes->at(-1).edges)
        {
            s_heal.emplace(i);
        }
        hstable.emplace(mygraph->nodes->at(-1));
        int ans = 0;
        while (!s_heal.empty())
        {
            Edge temp = s_heal.top();
            s_heal.pop();
            Node node = *temp.toNode;
            if (hstable.find(node) == hstable.end())
            {
                ans+=temp.weight;
                hstable.emplace(node);
                for (Edge i: *node.edges)
                {
                    s_heal.emplace(i);
                }
            }
        }
        return ans;
    }
private:
    Graph *mygraph;
};
class Solution {
public:
    int minCostToSupplyWater(int n, vector& wells, vector>& pipes) {
        Creator zj = Creator(wells,pipes);
        return zj.pmintree();
    }
};

1584. 连接所有点的最小费用
给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。

struct Myedges{
    int from;
    int to;
    int weight;
    Myedges(int from,int to,int weight):from(from),to(to),weight(weight){}
};
struct cmp{
    bool operator()(Myedges &a,Myedges &b)
    {
        return a.weight>b.weight;
    }
};
class Solution {
public:
    int minCostConnectPoints(vector>& points) {
        int myvec[points.size()][points.size()];   //出发点与点之间的边权重值
        for (int i = 0;i hstable;                                     //点
        priority_queue,cmp> s_heal;   //边
        int out = 0;
        hstable.emplace(0);                                   //从第0个点开始
        for (int i = 1;i

{
 public:
 /**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 返回最小的花费代价使得这n户人家连接起来
 * @param n int n户人家的村庄
 * @param m int m条路
 * @param cost intvector> 一维3个参数，表示连接1个村庄到另外1个村庄的花费的代价
 * @return int
 */
 int miniSpanningTree(int n, int m, vector& cost) {
    for (int i = 0;i{cost[i][1],cost[i][0],cost[i][2]});
    }
    Creator zj = Creator(cost);
    return zj.ptree();
}

};

#### [1168. 水资源分配优化](https://leetcode-cn.com/problems/optimize-water-distribution-in-a-village/)


村里面一共有 n 栋房子。我们希望通过建造水井和铺设管道来为所有房子供水。
对于每个房子 i，我们有两种可选的供水方案：
一种是直接在房子内建造水井，成本为 wells[i]；
另一种是从另一口井铺设管道引水，数组 pipes 给出了在房子间铺设管道的成本，其中每个 pipes[i] = [house1, house2, cost] 代表用管道将 house1 和 house2 连接在一起的成本。当然，连接是双向的。

请你帮忙计算为所有房子都供水的最低总成本。
 输入：n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
 输出：3
 解释：
 上图展示了铺设管道连接房屋的成本。
 最好的策略是在第一个房子里建造水井（成本为 1），然后将其他房子铺设管道连起来（成本为 2），所以总成本为 3。

最小生成树，树形结构，可以借用技巧，加辅助点，就像这道一样，将wells[i]转换成连向一个特殊点的权重，这样就转换成求最小生成树的问题，不然的话，还要考虑还要考虑要用那个水井，如果建一个水井的成本比连通的成本还要低的情况，就会变得很复杂。学习这种灵活转变的思想。一种技巧

```c++
class Node;
class Edge;
class Graph;
class Creator;
class Node{
public:
    int value;
    vector *edges = nullptr;
    Node(int a):value(a){
        edges = new vector();
    }
    bool operator <(const Node& a)const
    {
        return valueb.weight;
    }
};
class Graph{
public:
    unordered_map *nodes = nullptr;
    Graph()
    {
        nodes = new unordered_map();
    }
    ~Graph()
    {
        for (auto i:*nodes)
        {
            delete i.second.edges;
        }
        delete nodes;
    }
};
class Creator{
public:
    Creator(const vector& wells,const vector>& pipes)
    {
        mygraph = new Graph();
        mygraph->nodes->emplace(-1,Node(-1));  //水库,这个思想最重要
        for (int i = 0;inodes->emplace(to,Node(to));
            Node* fromNode = &mygraph->nodes->at(from);
            Node* toNode = &mygraph->nodes->at(to);
            fromNode->edges->emplace_back(move(Edge(weight,fromNode,toNode)));
            toNode->edges->emplace_back(move(Edge(weight,toNode,fromNode)));
        }
        for (int i = 0;inodes->at(from);
            Node* toNode = &mygraph->nodes->at(to);
            fromNode->edges->emplace_back(move(Edge(weight,fromNode,toNode)));
            toNode->edges->emplace_back(move(Edge(weight,toNode,fromNode)));
        }
    }
    ~Creator()
    {
        delete mygraph;
    }
    int pmintree()
    {
        priority_queue,cmp> s_heal;
        set hstable;
        for (Edge i:*mygraph->nodes->at(-1).edges)
        {
            s_heal.emplace(i);
        }
        hstable.emplace(mygraph->nodes->at(-1));
        int ans = 0;
        while (!s_heal.empty())
        {
            Edge temp = s_heal.top();
            s_heal.pop();
            Node node = *temp.toNode;
            if (hstable.find(node) == hstable.end())
            {
                ans+=temp.weight;
                hstable.emplace(node);
                for (Edge i: *node.edges)
                {
                    s_heal.emplace(i);
                }
            }
        }
        return ans;
    }
private:
    Graph *mygraph;
};
class Solution {
public:
    int minCostToSupplyWater(int n, vector& wells, vector>& pipes) {
        Creator zj = Creator(wells,pipes);
        return zj.pmintree();
    }
};

1584. 连接所有点的最小费用
给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。

struct Myedges{
    int from;
    int to;
    int weight;
    Myedges(int from,int to,int weight):from(from),to(to),weight(weight){}
};
struct cmp{
    bool operator()(Myedges &a,Myedges &b)
    {
        return a.weight>b.weight;
    }
};
class Solution {
public:
    int minCostConnectPoints(vector>& points) {
        int myvec[points.size()][points.size()];   //出发点与点之间的边权重值
        for (int i = 0;i hstable;                                     //点
        priority_queue,cmp> s_heal;   //边
        int out = 0;
        hstable.emplace(0);                                   //从第0个点开始
        for (int i = 1;i

leetcode笔记

输入处理

自定义排序

大根堆的自定义排序

451. 根据字符出现频率排序

vector的自定义排序

map,set存放 类或结构体

981. 基于时间的键值存储

哈希表存放 类或结构体

56. 合并区间

剑指 Offer 45. 把数组排成最小的数

剑指 Offer 50. 第一个只出现一次的字符

排序

冒泡排序

选择排序

插入排序

希尔排序

归并排序

堆排序

桶排序

快排

面试题 17.14. 最小K个数

查找

二分查找

剑指 Offer 11. 旋转数组的最小数字

顺序查找

哈希表查找

128. 最长连续序列

二叉排序树查找

双指针

167.给定一个已按照 升序排列 的整数数组 numbers ，请你从数组中找出两个数满足相加之和等于目标数 target 。

11. 盛最多水的容器

209. 长度最小的子数组

面试题 16.16. 部分排序

链表

删除链表的倒数第 N 个结点

61. 旋转链表

剑指 Offer 35. 复杂链表的复制

1721. 交换链表中的节点

24. 两两交换链表中的节点

328. 奇偶链表

链表中倒数最后k个结点

剑指offer

数组

剑指 Offer 03. 数组中重复的数字f

二叉树

1.前序、中序、后序遍历，输出tree的值

2.重新构建一颗二叉树

106. 从中序与后序遍历序列构造二叉树

剑指 Offer 37. 序列化二叉树

4.BST 搜索二叉树：左节点比根节点小，右节点比根节点大。左子树的最大值比根节点小，右子树的最小值比根节点大。二叉搜索树（BST）的中序遍历是有序的

700. 二叉搜索树中的搜索

783. 二叉搜索树节点最小距离

897. 递增顺序搜索树

5.平衡二叉树：左子树和右子树的高度相差小于1

110. 平衡二叉树

6.满二叉树：深度h 和 节点个数n 满足：2^h-1 = n

7.求两节点的公共祖先

236. 二叉树的最近公共祖先

8.求前驱或者后继节点 ：前驱后继指的是中序遍历中的顺序

9.宽度优先遍历：需要用到到queue这个结构辅助

剑指 Offer 32 - II. 从上到下打印二叉树 II

9.完全二叉树：不存在只有右子树没有左子树的情况。如果孩子不双全，那么后面的节点都是叶几点。

1382. 将二叉搜索树变平衡

深度优先搜索（DFS）

104. 二叉树的最大深度

位运算

190. 颠倒二进制位

9. 回文数

504. 七进制数

滑动窗口

数组、字符串

输入格式

输出格式

前缀树-查、建操作

648. 单词替换

基本数学

1.求质数；

2.求最大公因数、最小公倍数

输入格式

map,set存放类或结构体

哈希表存放类或结构体

167.给定一个已按照升序排列的整数数组 numbers ，请你从数组中找出两个数满足相加之和等于目标数 target 。

6.满二叉树：深度h 和节点个数n 满足：2^h-1 = n

8.求前驱或者后继节点：前驱后继指的是中序遍历中的顺序

2020年真题地铁打卡