机器学习(四)
一、特征的预处理——归一化
(一)、归一化数值运算
为了便于后续算法的计算,我们将原始数据进行归一化,归一化主要是为了数据处理方便,把数据映射到0~1范围之内处理,更加便捷快速。公式如下:

X表示某一个元素的数值大小。max为该特征的最大值,min为该特征的最小值。在机器学习的数据中,往往一列为一个特征。mx和mi为默认指定区间,我们往往默认为是1,0
例如有三个样本,具体如下:
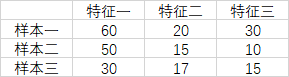
我们现在计算第一个样本的第一个特征归一化之后的数据:
X’=(60-30)/(60-30)=1
x’’=1*(1-0)+0=1
则最终的归一化结果为1.
(二)归一化的优点:
(1)归一化后加快了梯度下降求最优解的速度。
(2)归一化有可能提高精度(归一化是让不同维度之间的特征在数值上有一定的比较性,例如同一批样本下两个特征相比,第一个特征为万级数字,第二个特征为小数级数字,则在后续的预测的结果往往受第一个特征的影响较大。我们将所有特征归一化之后则消除了这样的弊端)。
(三)sklearn中的归一化API——MinMaxScaler
具体实现代码如下:
from sklearn.preprocessing import MinMaxScaler
def mm():
"""
对特征进行归一化处理
"""
# 需要处理的原始数据
data = [[1, 2, 3],
[8, 9, 7],
[5, 7, 9]]
# 实例化,feature_range不进行设定时默认为0,1。也可以自己设定一个区间
MM = MinMaxScaler(feature_range=(0, 1))
result = MM.fit_transform(data)
print(result)
处理后的结果如下:
[[0. 0. 0. ]
[1. 1. 0.66666667]
[0.57142857 0.71428571 1. ]]
(四)归一化应用场景

从上述公式我们可以看出,归一化处理对样本的最大最小值的影响较大,因此,这种方法的鲁棒性较弱。故这种方式只适合小数据样本的操作。
二、特征预处理——标准化
归一化由于受样本数据的影响较大,故在实际应用场景中并不是很常用。下面再简单介绍一下在实际场景中应用较多的一个预处理方法——标准化。标准化也是将数据变化到均值为0,标准差为1的范围内。
(一)、标准化的计算

与归一化的处理范围一样,标准化作用于样本中的某一特征。mean为平均值,σ为标准差。
方差公式如下:
![]()
其M为平均值,即为上式中的mean,n为样本总个数。标准差(σ)即为方差的开方。方差的目的主要是评估数据的稳定性,方差越大数据的稳定性越弱。
(二)、标准化优点
相较于归一化来讲,在大规模的数据处理的情况下,其鲁棒性较强。从公式可以看出,由于数据量较大,少量的异常点对整个特征的平均值影响较小,故对方差差的影响也会变小。
(三)、sklearn中标准差的API——StandardScaler
def stand():
"""
对特征进行标准化
:return:
"""
data = [[1, 2, 3],
[8, 9, 7],
[5, 7, 9]]
std = StandardScaler()
result = std.fit_transform(data)
# 打印标准化后的数据
print(result)
运算后的结果为:
[[-1.27872403 -1.35873244 -1.33630621]
[ 1.16247639 1.01904933 0.26726124]
[ 0.11624764 0.33968311 1.06904497]]
(四)、标准化应用补充
标准化主要应用于数据量较大,且数据比较嘈杂的情况下。但是随着数据量的增大,难免会有些数据的缺失,这里我们需要对缺失数据的样本进行删除或补充缺失值。补充缺失值的方法有以下几种,第一种就是可以将每一列的平均值补充到缺失值的位置,第二种方法就是将每一列的中值补充到缺失值的位置,第三种方法就是将每一列的众数补充到缺失值的位置,第四种方法就是将指定的数值补充到缺失值的位置
在sklearn也有其对应的API。即为:SimpleImputer
def im():
"""
特征中缺失值的处理
:return:
"""
data = [[1, 2, 3],
[8, np.NAN, 7],
[5, 7, 9]]
mm = SimpleImputer(missing_values=np.NAN, strategy='mean', fill_value=1)
""" missing_values默认为np.nan格式的,也可以按照自身情况自行设定,
strategy有四种情况:
mean均值补充、median中值补充、most_frequent众数补充、constant按照fill_value中的内容补充"""
result = mm.fit_transform(data)
print(result)
输出结果为:
[[1. 2. 3. ]
[8. 4.5 7. ]
[5. 7. 9. ]]