深度学习笔记
深度学习笔记
- 前言
- 学习内容
-
- 什么是深度学习？
- * 监督式学习supervised learning和非监督式学习
- * 数据类型的两种形式
- * Binary Classification 二分类
- * Logistic Regression
- * Computation graph计算图
- * Broadcasting Python 中的广播
- * Neural Networks 浅层神经网络
- * Deep L - Layer neural network 深层神经网络
- * 优化神经网络模型
- * Vanishing and Exploding gradients 梯度消失 和 梯度爆炸
- * 梯度检查 Numerical approximation of gradients
- * Exponentially weighted averages 指数加权平均
- * Gradient descent with momentum 动量梯度下降算法
- * Tuning Process 调整超参数
- * TensorFlow
- * 卷积神经网络基础
- * 深度卷积模型：案例研究
- 后记
前言
- 补档，此前为用幕布软件记录，转到这里可能有格式上的问题
- 学习主要为依靠吴恩达视频
学习内容
本周主要认真学习了吴恩达深度学习第二周视频，内容包括：逻辑回归、梯度下降、损失函数、广播等内容以及其相关的Python代码的落实。
什么是深度学习？
-
什么是深度学习？
-
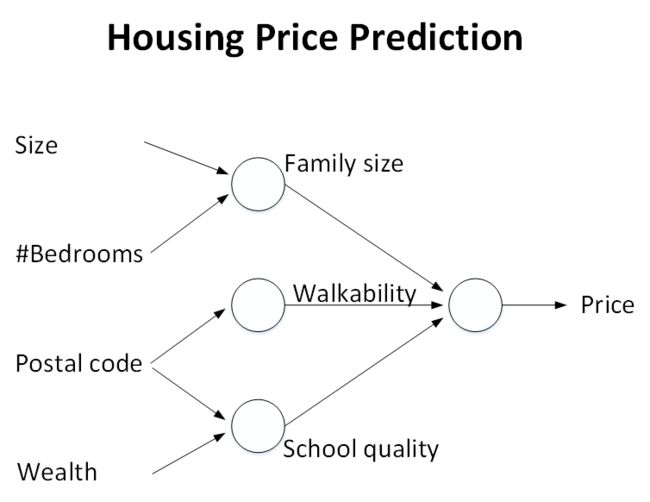
深度学习就是一个更复杂的神经网络
-
神经网络
-
如图所示是，一个最简单的例子，就是输入X，可以弄出来y，y= f(x)
-
就是说，有一些已知的面积x和价格的数据集y，而网络的目的就是做一条直线来拟合。这种模型和拟合的曲线就可以理解为一个简单的神经网络
-
大型的神经网络就是由一堆的这样的神经元组成，就像下面这个图片，大型的的神经网络是由一大堆的神经元组成的，就每一个小神经元都是有输入有输出的一个函数；最终形成输出
-
-
左边的输入的地方是输入层，中间的神经元所在的地方是隐藏层，
-
-
-
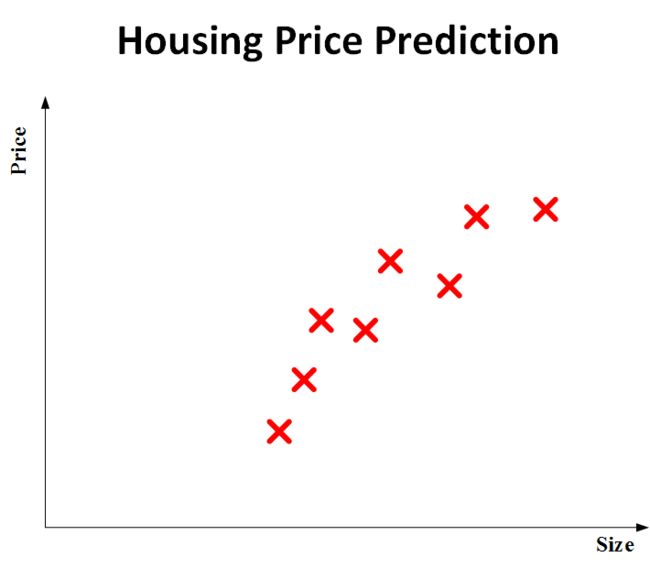
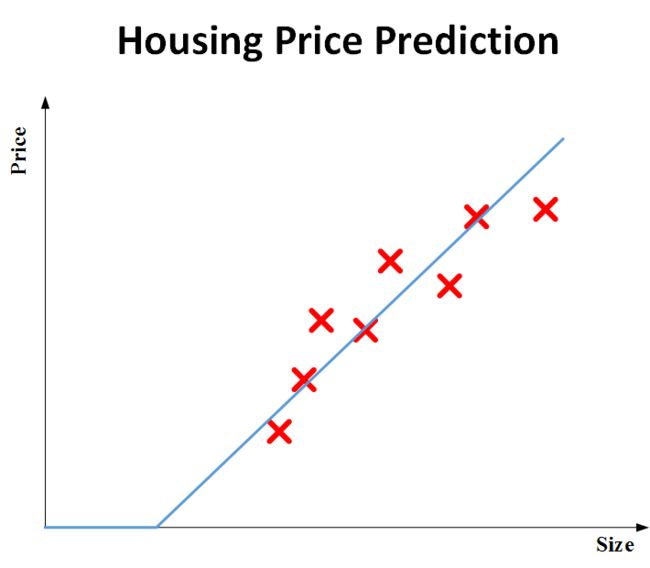
神经元neuron
- 上面这个拟合的曲线就是一个神经元，神经元的功能就是实现这个曲线函数f(x)的功能
-
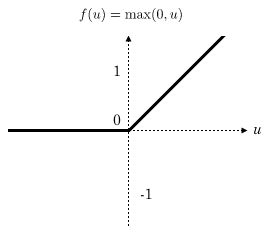
ReLU 函数 Rectified Linear Unit
-
比较常见的神经网络应用函数
-
f(x) = max(0,u)
-
-
-
* 监督式学习supervised learning和非监督式学习
* 有监督和非监督的本质区别就是，是否已知训练样本的输出y
* 对于图像处理，需要卷积神经网络CNN
* 数据类型的两种形式
* Structured Data 和 Unstructured Data 结构式数据和非结构式数据
* 结构式数据就是有实际意义的数据，是实际的数字，有实际的现实意义和物理意义
* 非结构式数据就是比如图片、音频等这些，不能用实际的物理来描述的
* Binary Classification 二分类
* 二分类就是输出y只有{0，1}或者{-1，1}两耳光离散值的情况，比如看图片是否有猫，就是有或者没有
* 
* 如上面的第二个图，这是一个比较经典的二分类问题。对于一个图片，RGB三个通道。在输入时候，要将（64，64，3）的输入值转换为一维再计算，转化为（64\*64\*3，1）的一维向量
* x是列向量，维度一般记为nx，如果训练样本共有m张图片，那么整个训练样本x就是一个矩阵，维度就是（nx,m)
* 这里使用的是nx，m是为了方便
* 所有的输出y就是（1，m）
* Logistic Regression
* 逻辑回归的线性预测输出：
* 公式如下: y^=wT+b\\widehat{y} = w^T + by=wT+b
* 这个线性的预测的结果区间是整个实数，由于要求整个在【0，1】之间，由此必须引入Sigmoid函数
* Sigmoid函数：
* 11+e−z\\frac{1}{1 + e^{-z}}1+e−z1
* 该函数曲线如图所示。可以看到，可以将输出限制在0和1之间，在z等于0的时候，函数值是0.5
* 
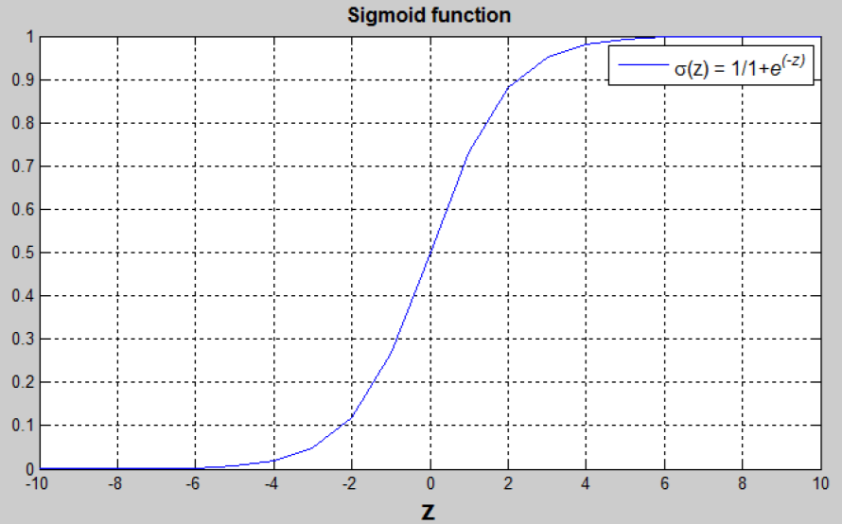
* 意义：将逻辑回归的输出限定在【0，1】之间
* sigmoid函数的一阶导数：σ′(z)=σ(z)(1−σ(z))\\sigma ' (z) = \\sigma (z)(1-\\sigma(z))σ′(z)=σ(z)(1−σ(z))
* 在引入Sigmoid函数之后，逻辑回归的公式变成了
* y^=Sigmoid(wTx+b)=σ(wTx+b)\\widehat y = Sigmoid(w^T x + b) = \\sigma(w^Tx + b)y=Sigmoid(wTx+b)=σ(wTx+b)
* 在上述公式中，www和 bbb 都是未知数，我们想要得到最优解的话，就必须使用 Cost function 来进行优化，也就是说这个Cost function是为了找到最合适的W和B
* 如果有多个训练样本，那么一般是使用上标来表示对应的样本。比如(x(i),y(i))(x^{(i)} ,y^{(i)})(x(i),y(i)) 就是表示第iii个样本
* Cost function损失函数
* 损失函数的意义是为了衡量错误大小，也就是说，这个函数的值越小越好；
* 针对逻辑回归，我们为了得到全局最优解，构建了一个convex的Loss function，具体公式如下
* L(y^,y)=−(ylogy^+(1−y)log(1−y^))L(\\widehat y, y) = - (y log\\widehat y + (1-y)log(1-\\widehat y))L(y,y)=−(ylogy+(1−y)log(1−y))
* 具体的逻辑是这样的
* 如果你y=1，那么函数就变成了L(y^,y)=−logy^L(\\widehat y, y ) = -log\\widehat yL(y,y)=−logy,这个函数，当你的预测 y^\\widehat yy 接近1，那么损失函数就接近0
* 如果你 y = 0, 那么函数就变成了L(y^,y)=−log（1−y^）L(\\widehat y, y ) = -log（1-\\widehat y）L(y,y)=−log（1−y），就是你的预测接近0，最终结果也接近0
* 针对m个样本的话，Cost function应该转化为下面这个形式，就是普通的损失函数加一起求平均值，最终的公式如下：
* J(w,b)=1m∑i=1mL(y^(i),y(i))=−1m∑i=1m\[y(i)logy^(i)+(1−y(i)log(1−y(i))\]J(w,b) = \\frac{1}{m} \\sum_{i=1}{^m}{L(\\widehat y^{(i)}, y^{(i)}}) = - \\frac{1}{m} \\sum_{i=1}{^m}{\[ y^{(i)} log \\widehat y^{(i)} + (1-y^{(i)}log (1-y^{(i) })\]}J(w,b)=m1∑i=1mL(y(i),y(i))=−m1∑i=1m\[y(i)logy(i)+(1−y(i)log(1−y(i))\]
* Gradient Descent 梯度下降
* 梯度下降算法是用来计算最合适的w和b的值的算法，从而可以来最小化m个训练样本的Cost function，也就是J(w,b)J(w,b)J(w,b)
* 我们的损失函数的形状大概如下图所示，梯度下降算法的思想就是分别沿着w和b的偏导数的反方向前进一小步，不断修正w和b的取值，不断接近全局最小值。
* 
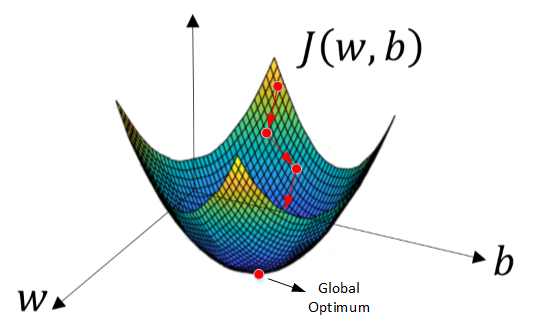
* w和b的修正算法表达如下：
* w:=w−α∂J(w,b)∂ww:=w-\\alpha \\frac{\\partial J(w,b)}{\\partial w}w:=w−α∂w∂J(w,b)
* b:=b−α∂J(w,b)∂bb: =b-\\alpha\\frac{\\partial J(w,b)}{\\partial b}b:=b−α∂b∂J(w,b)
* α\\alpha α是学习因子，表示梯度下降的不乏长度，α\\alphaα越大，更新的越大，反之更小。
* Computation graph计算图
* 神经网络的训练过程是包括两个过程：
* Forward Propagation正向传播
* 从输入到输出，通过神经网络计算得到预测输出
* Back Propagation 反向传播
* 从输出到输入，通过这个过程对参数w和b进行优化并计算梯度
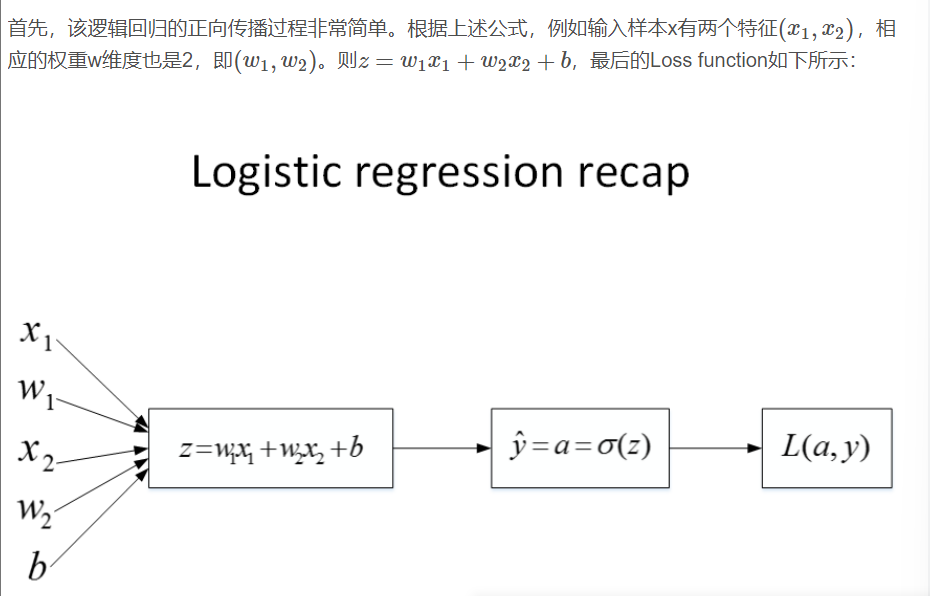
* 逻辑回归的梯度计算 Logistic Regression Gradient Descent
* 推导过程如图
* 
* 
* 最终结果：
* w1:=w1−αdw1w1:=w1 - \\alpha dw1w1:=w1−αdw1
* w2:=w2−αdw2w2:=w2-\\alpha dw2w2:=w2−αdw2
* b:=b−αdbb:=b-\\alpha dbb:=b−αdb
* 就是这么个正向/反向传递过程
* 
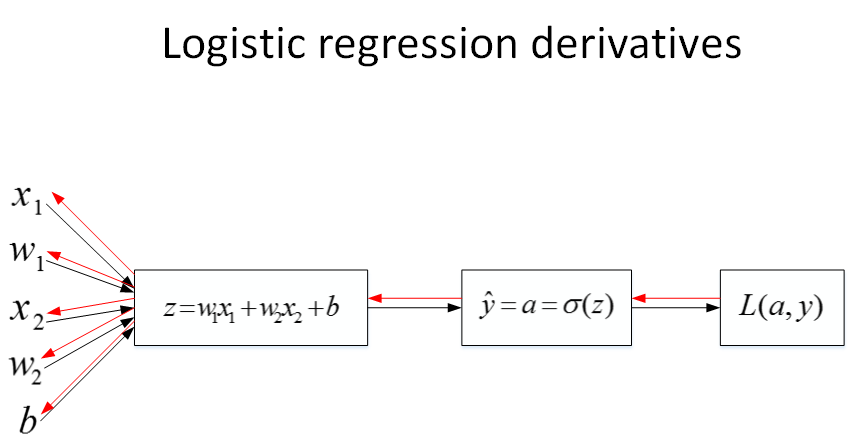
* 如果训练样本有m个，那么最终结果就是
* dw1=1m∑i=1mx1(i)(a(i)−y(i))dw1 = \\frac{1}{m} \\sum_{i=1}^{m} {x_1^{(i)}(a^{(i)}-y^{(i)})}dw1=m1∑i=1mx1(i)(a(i)−y(i))
* dw2=1m∑i=1mx2(i)(a(i)−y(i))dw2 = \\frac{1}{m} \\sum_{i=1}^{m} {x_2^{(i)}(a^{(i)}-y^{(i)})}dw2=m1∑i=1mx2(i)(a(i)−y(i))
* db=1m∑i=1m(a(i)−y(i))db = \\frac{1}{m} \\sum_{i=1}^{m}(a^{(i)}-y^{(i)})db=m1∑i=1m(a(i)−y(i))
* 最终迭代过程
* w1:=w1−αdw1w1:=w1 - \\alpha dw1w1:=w1−αdw1
* w2:=w2−αdw2w2:=w2-\\alpha dw2w2:=w2−αdw2
* b:=b−αdbb:=b-\\alpha dbb:=b−αdb
* 实际的计算过程就是不断重复n次
* Broadcasting Python 中的广播
* 广播机制就是，输入中的所有的数组都自动向最长最大的数组看起，不足的或者少的都自动补齐
* 简单理解就是，Python可以对不同的维度的矩阵做各种四则混合运算，但是要至少保证有一个维度是相同的
* 
* Neural Networks 浅层神经网络
* 神经网络与逻辑回归类似，比逻辑回归多了一层隐藏层或者中间层，就是多重复了一次计算
* 单隐藏层的神经网络结构
* 具体示意图如下图所示：
* 
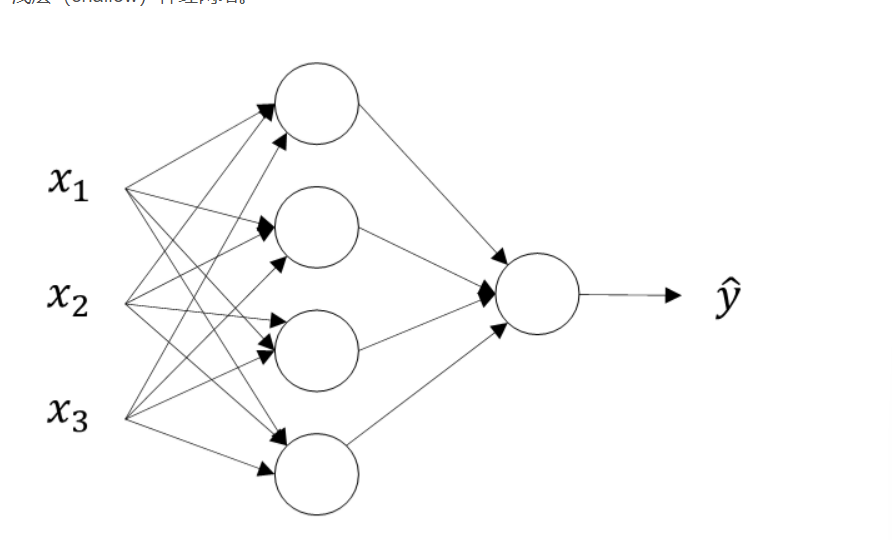
* 看这个图也比较容易理解，就是，先把每一个x都计算过了之后，结果统一作为一个矩阵再计算一次。
* 上图从左到右计算，x那一层就是输入层input layer，第二层就是隐藏层Hidden Layer，第三层是输出层 Output layer
* 通常把输入矩阵x记为a\[0\]a^{\[0\]}a\[0\]，把隐藏层输出记为a\[1\]a^{\[1\]}a\[1\]，用下标表示第一个神经元。如：a1\[0\]a^{\[0\]}_{1}a1\[0\]表示隐藏层第一个神经元，就是最上面的那个。
* 那么隐藏层的最终输出如下
* a\[1\]a^{\[1\]}a\[1\] = \[a1\[1\]a2\[1\]a3\[1\]a4\[1\]\]\\left\[\\begin{matrix} a^{\[1\]}\_1\\\a^{\[1\]}\_2\\\a^{\[1\]}\_3\\\a^{\[1\]}\_4\\end{matrix}\\right\]⎣⎢⎢⎢⎢⎡a1\[1\]a2\[1\]a3\[1\]a4\[1\]⎦⎥⎥⎥⎥⎤
* 这种神经网络被叫做两层神经网络，因为输入层的神经网络是不被记入的，所以输入层上面被记录为【0】
* 最终的输出层的输出标记为a\[2\]a^{\[2\]}a\[2\]，也被称作 y^\\widehat yy
* 正向传播：
* 第一层：从输入层到隐藏层，用上标【1】表示
* z\[1\]=Q\[1\]x+b\[1\]z^{\[1\]} = Q ^ {\[1\]} x + b ^ {\[1\]}z\[1\]=Q\[1\]x+b\[1\]
* a\[1\]=σ(z\[1\])a^{\[1\]} = \\sigma(z^{\[1\]})a\[1\]=σ(z\[1\])
* 第二层：从隐藏层到输出层，用上标【2】表示
* z\[2\]=W\[2\]a\[1\]+b\[2\]z^{\[2\]} = W^{\[2\]}a^{\[1\]} + b^{\[2\]}z\[2\]=W\[2\]a\[1\]+b\[2\]
* a\[2\]=W\[2\]a\[1\]+b\[2\]a^{\[2\]} = W^{\[2\]}a^{\[1\]} + b^{\[2\]}a\[2\]=W\[2\]a\[1\]+b\[2\]
* 看这个图就是一个正向传播的流程，就是先正常算一次逻辑回归，这个结果作为新的x输入进去，然后再结合新的权重w喝b，重新计算一遍逻辑回归，最终计算损失函数
* 
* 神经网络的计算 Computing
* 两层神经网络的计算，就是从输入层到隐藏层对应一次的逻辑回归运算，从隐藏层到输出层对应一次逻辑回归运算
* 从输入层到隐藏层的计算公式
* zn\[1\]=wn\[1\]Tx+bn\[1\]z^{\[1\]}\_n = w^{\[1\]T}\_n x + b^{\[1\]}_nzn\[1\]=wn\[1\]Tx+bn\[1\]
* an\[1\]=σ(zn\[1\])a^{\[1\]}\_n = \\sigma(z^{\[1\]}\_n)an\[1\]=σ(zn\[1\])
* 这里的下标n是从1到4，上标永远为1，因为是隐藏层
* 从隐藏层到输出层
* z1\[2\]=w1\[2\]Ta\[1\]+b1\[2\]z^{\[2\]}\_1 = w^{\[2\]T}\_1 a^{\[1\]} + b^{\[2\]}_1z1\[2\]=w1\[2\]Ta\[1\]+b1\[2\]
* a1\[2\]=σ(z1\[2\])a^{\[2\]}\_1 = \\sigma(z^{\[2\]}\_1)a1\[2\]=σ(z1\[2\])
* 其中，a\[1\]a^{\[1\]}a\[1\] = \[a1\[1\]a2\[1\]a3\[1\]a4\[1\]\]\\left\[\\begin{matrix} a^{\[1\]}\_1\\\a^{\[1\]}\_2\\\a^{\[1\]}\_3\\\a^{\[1\]}\_4\\end{matrix}\\right\]⎣⎢⎢⎢⎢⎡a1\[1\]a2\[1\]a3\[1\]a4\[1\]⎦⎥⎥⎥⎥⎤
* 为了提升计算效率，往往采取矩阵运算的方式
* 
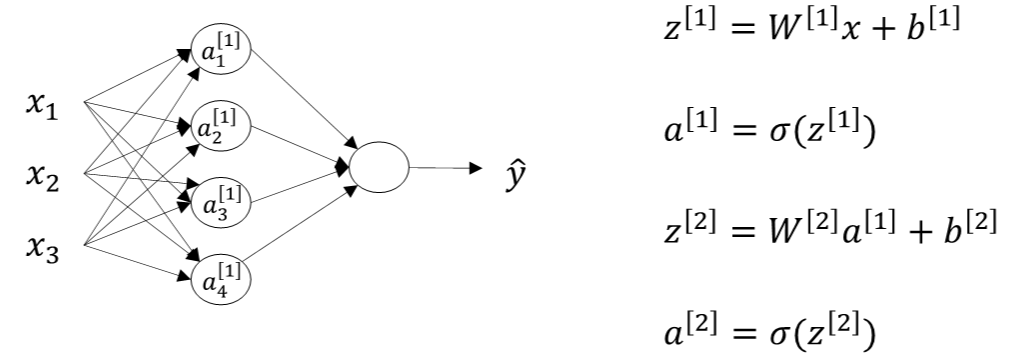
* 激活函数 Activation Function
* 其实就是之前的那个sigmoid函数就是激活函数的一种，这种激活函数的作用就是把输出限制在0 - 1 或者-1 到 1 之间，有多种激活函数，不同的有不同的优劣点，也有不同的取值范围
* 激活函数一定要非线性激活函数，如果全是现行的激活函数，那么整个结构就类似一个简单的逻辑回归模型，就没啥用价值了；
* 如果是预测问题而不是分类问题，y是连续的话，可以用线性函数；
* 如果输出y恒为正数，可以用ReLU激活函数
* sigmoid 函数
* 公式： a=11+e−za = \\frac{1}{1 + e^{-z}}a=1+e−z1
* 图像：
* 
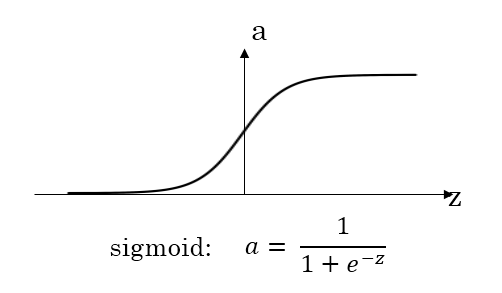
* 优点：二分类的输出取值为从0到+1，所以输出层的激活函数一般取sigmoid函数
* 缺点：当z很大的时候，函数的斜率很平，这样的话梯度下降特别慢，应该让z的取值在零附近，从而提高梯度下降算法的运算速度；这也是为什么隐藏层用tanh更好
* 梯度（导数）
* g(z)=11+e−zg(z) = \\frac{1}{1 + e^{-z}}g(z)=1+e−z1
* g′(z)=ddzg(z)=g(z)(1−g(z))=a(1−a)g'(z) = \\frac{d}{dz}g(z) = g(z) (1-g(z)) = a(1-a)g′(z)=dzdg(z)=g(z)(1−g(z))=a(1−a)
* tanh 函数
* 公式：tanh:a=ez−e−zez+e−ztanh: a = \\frac{e^z - e^{-z}}{e^z + e^{-z}}tanh:a=ez+e−zez−e−z
* 图像：
* 
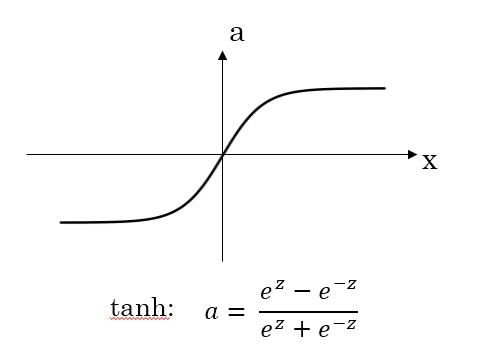
* 优点：这个函数的取值范围是【-1，+1】，那么隐藏层的输出就被限定在这个区间里了；这样的均值是0的一组数据传到输出层，数据就可以归一化。所以这个函数一般用在隐藏层。
* 缺点：当z很大的时候，函数的斜率很平，这样的话梯度下降特别慢，应该让z的取值在零附近，从而提高梯度下降算法的运算速度；这也是为什么隐藏层用tanh更好
* 梯度（导数）
* tanh:a=g(z)=ez−e−zez+e−ztanh: a = g(z) = \\frac{e^z - e^{-z}}{e^z + e^{-z}}tanh:a=g(z)=ez+e−zez−e−z
* g′(z)=ddzg(z)=1−(g(z))2=1−a2g'(z) = \\frac{d}{dz} g(z) = 1 - (g(z))^2 = 1 - a^2g′(z)=dzdg(z)=1−(g(z))2=1−a2
* ReLU 函数
* 公式： a=max(0,z)a = max(0,z)a=max(0,z)
* 图像：
* 
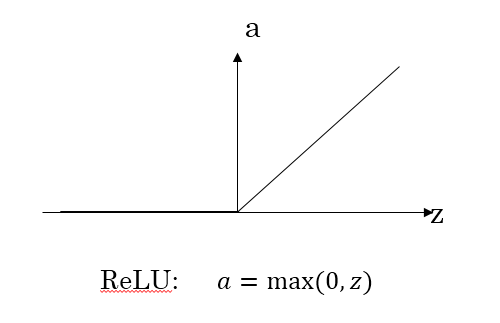
* 优点：z大于零的时候，梯度始终为1，不会影响梯度下降的速率
* 缺点：在z小于零的时候梯度始终为0 ， - 》Leaky ReLU
* 梯度（导数）
* a=g(z)=max(0,z)a = g(z) = max(0,z)a=g(z)=max(0,z)
* g′(z)={0,z<01,z≥0g'(z) = \\begin{cases} 0, &z<0\\\1, &z≥0\\end{cases}g′(z)={0,1,z<0z≥0
* Leaky ReLU 函数
* 公式：a=max(0.01z,z)a = max(0.01z, z)a=max(0.01z,z)
* 图像：
* 
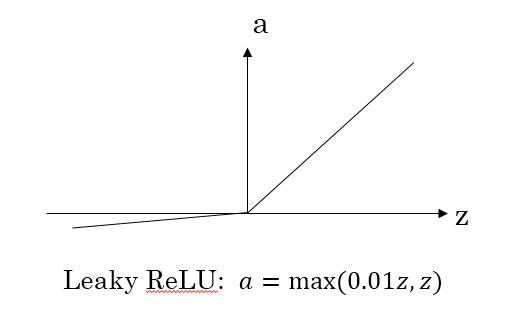
* 优点：
* z小于零的时候，梯度不是零
* 梯度（导数）
* g′(z)={0.01,z<01,z≥0g'(z) = \\begin{cases} 0.01, &z<0\\\1, &z≥0\\end{cases}g′(z)={0.01,1,z<0z≥0
* 总结：
* 如果是分类问题，输出层的激活函数一般选择sigmoid，隐藏层的激活函数一般是tanh，但是实际应用一般选择ReLU或者Leaky ReLU函数从而保证梯度下降的速度；
* 反向传播计算梯度
* 由于有两层，就是每个的w和b都要计算
* 最终结果：
* 输出层的参数：
* dZ\[2\]=A\[2\]−YdZ^{\[2\]} = A^{\[2\]} - YdZ\[2\]=A\[2\]−Y
* dW\[2\]=1mdZ\[2\]A\[1\]TdW^{\[2\]} = \\frac{1}{m} dZ^{\[2\]}A^{\[1\]T}dW\[2\]=m1dZ\[2\]A\[1\]T
* db\[2\]=1mnp.sum(dZ\[2\],axis=1,keepdim=Truedb^{\[2\]} = \\frac{1}{m} np.sum(dZ^{\[2\] },axis = 1, keepdim = Truedb\[2\]=m1np.sum(dZ\[2\],axis=1,keepdim=True
* 隐藏层的参数：
* dZ\[1\]=W\[2\]TdZ\[2\]∗g′(Z1)dZ^{\[1\]} = W^{\[2\]T}dZ^{\[2\]} * g'(Z^{1})dZ\[1\]=W\[2\]TdZ\[2\]∗g′(Z1)
* dW\[1\]=1mdZ\[1\]XTdW^{\[1\]} = \\frac{1}{m}dZ^{\[1\]} X^TdW\[1\]=m1dZ\[1\]XT
* db\[1\]=1mnp.sum(dZ\[1\],axis=1,keepdim=Truedb\[1\] = \\frac{1}{m}np.sum(dZ^{\[1\]},axis=1,keepdim = Truedb\[1\]=m1np.sum(dZ\[1\],axis=1,keepdim=True
* 图示
* 
* Random Initialization
* 意义
* 之前的逻辑回归的w和b都初始化为0，但是神经网络里不可以将W设置为零，但是可以将B全部初始化为0
* 如果权重W\[1\]W^{\[1\]} W\[1\] 和 W\[2\]W^{\[2\]}W\[2\] 全部为0，那么隐藏层的多个神经元就会永远一模一样，那么设置多个隐藏层神经元就没有意义了
* 解决方法：
* 将W随机初始化就好了
* 使用np.random,randn()函数
* 注意要×0.01，让他比较小，比较靠近0
* 就是如果用sigmoid函数，最好初始化到比较小的值
* Deep L - Layer neural network 深层神经网络
* 深层神经网络就是包含更多的隐藏层的神经网络，这个图片就是给出了两层和五层的例子
* 
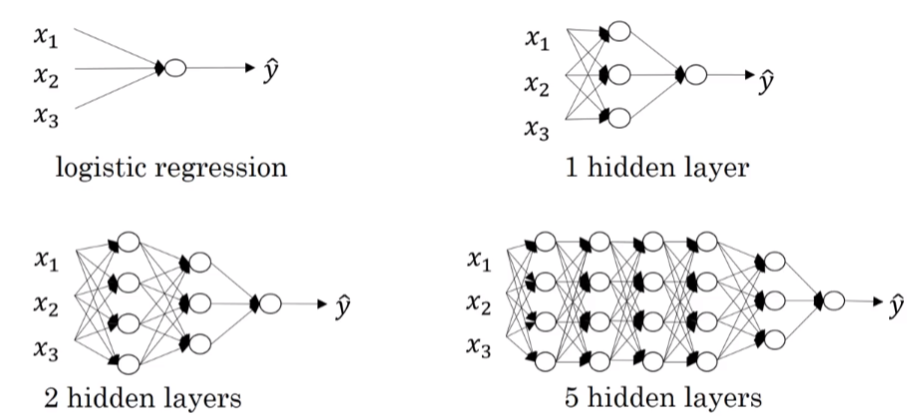
* 我们的命名规则只考虑隐藏层和输出层的个数，也就是说，上次学的浅层的神经网络是两层的，就只有一个隐藏层；L - layer 就是 L-1 个隐藏层
* 深层神经网络的正向传播 Forward Propagation
* 对于第一层
* z\[1\]=W1x+b\[1\]=W\[1\]a\[0\]+b\[1\]z^{\[1\] } = W^{1} x + b^{\[1\]} = W^{\[1\]} a^{\[0\]} + b^{\[1\]}z\[1\]=W1x+b\[1\]=W\[1\]a\[0\]+b\[1\]
* a\[1\]=g\[1\](z\[1\])a^{\[1\]} = g^{\[1\]} (z^{\[1\]})a\[1\]=g\[1\](z\[1\])
* 对于后续的几层
* z\[n\]=Wna+bn−1=W\[n\]a\[n−1\]+bnz^{\[n\]} = W^na + b^{n-1} = W^{\[n\]} a ^{\[n-1\]} + b^{n}z\[n\]=Wna+bn−1=W\[n\]a\[n−1\]+bn
* a\[n\]=g\[n\](z\[n\])a^{\[n\]} = g^{\[n\]} (z^{\[n\]})a\[n\]=g\[n\](z\[n\])
* 就是说，直接输入的内容在第一层经过逻辑回归的计算，然后后续的每一层的计算的输入值都是上一层的输出值
* 深层神经网络的反向传播： Backward Propagation
* 输入是da\[l\]da^{\[l\]}da\[l\]，输出是da\[l−1\],dw\[l\],db\[l\]da^{\[l-1\]}, dw^{\[l\]}, db^{\[l\]}da\[l−1\],dw\[l\],db\[l\]
* dz\[l\]=da\[l\]∗g\[l\]′(z\[l\])dz^{\[l\]} = da^{\[l\]} * g^{\[l\]'}(z^{\[l\]})dz\[l\]=da\[l\]∗g\[l\]′(z\[l\])
* dW\[l\]=dz\[l\]∗a\[l−1\]dW^{\[l\]} = dz^{\[l\]}* a^{\[l-1\]}dW\[l\]=dz\[l\]∗a\[l−1\]
* db\[l\]=dz\[l\]db^{\[l\]} = dz^{\[l\]}db\[l\]=dz\[l\]
* da\[l−1\]=W\[l\]T∗dz\[l\]da^{\[l-1\]} = W^{\[l\] T} * dz^{\[l\]}da\[l−1\]=W\[l\]T∗dz\[l\]
* dz\[l\]=W\[l+1\]T∗dz\[l+1\]∗g\[l\]′(z\[l\])dz^{\[l\]} = W^{\[l+1\]T} * dz^{\[l+1\] } * g^{\[l\]'}(z^{\[l\]})dz\[l\]=W\[l+1\]T∗dz\[l+1\]∗g\[l\]′(z\[l\])
* 深层神经网络的必要性与意义
* 一个人脸识别的例子
* 如下图所示。经过训练，神经网络第一层所做的事就是从原始图片中提取出人脸的轮廓与边缘，即边缘检测。这样每个神经元得到的是一些边缘信息。神经网络第二层所做的事情就是将前一层的边缘进行组合，组合成人脸一些局部特征，比如眼睛、鼻子、嘴巴等。再往后面，就将这些局部特征组合起来，融合成人脸的模样。
* 就是说，这么多层，每一层都有自己的功能和作用，每一层都能提取出一定的特征。模型从浅到深，可以从边缘到局部特征到整体，从简单到复杂。
* 深层网络还可以减少神经元的数量，从而减少计算量
* 在实际问题中，先选择层数较少的神经网络模型，对于复杂的问题再使用深层的神经网络模型，符合“奥卡姆剃刀定律”，如无必要，勿增实体
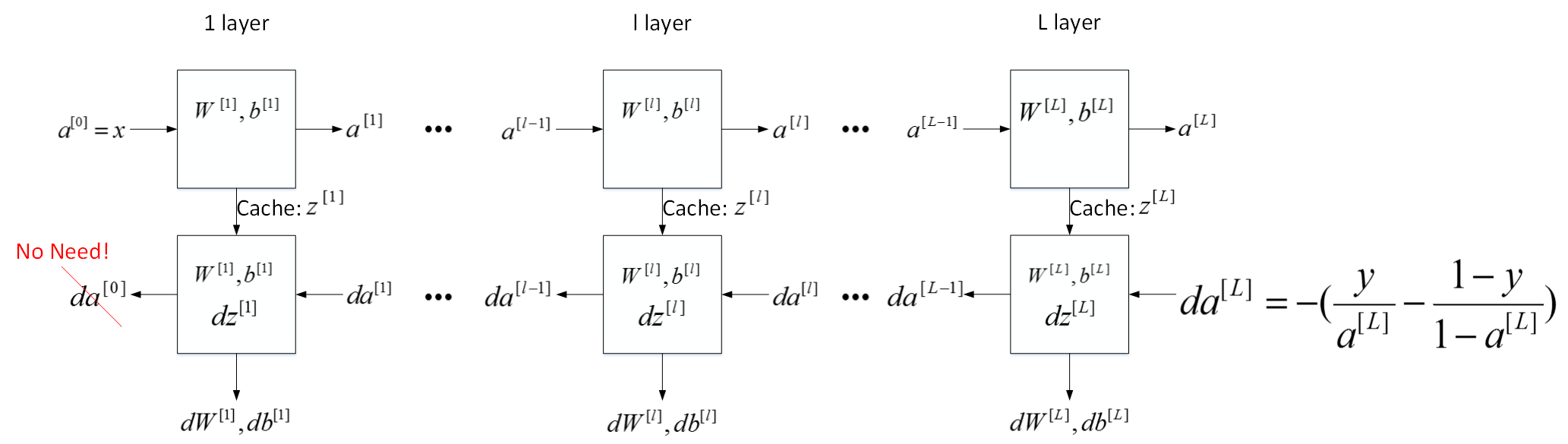
* 对于神经网络的所有层，整体的流程块图正向传播的过程和反向传播的示意图
* 
* 参数parameter和超参数Hyperparameters
* 参数就是W和b，超参数就是学习速率α\\alphaα 迭代次数NNN，神经网络层数LLL，各层神经元个数n\[l\]n^{\[l\]}n\[l\]，激活函数g(z)g(z)g(z)
* 超参数就是可以决定参数W和b的值，所以叫超参数
* 优化神经网络模型
* 样本数据集
* Train sets
* 训练集，用来训练算法模型
* Dev sets
* 用来验证不同算法的表现情况，从中选择表现最好的算法模型
* Test sets
* 用来测试最好算法的实际表现
* 一般情况下，Train: Test = 7:3; 如果有Dev sets， 比例设置为6：2：2
* 对于大数据样本，Train: Dev: Test sets = 98:1:1这样的比例，就是说，数据量越大，相应的Dev/Test的比例可以设置相对较低
* 常常在实际中，训练样本和测试样本的分布不匹配，就是可能训练样本时网络下载的高清版本，而实际的用户上传的低画质版本
* 通常可以将现有的训练样本做处理来扩大样本数量，比如图片翻转，随机噪声
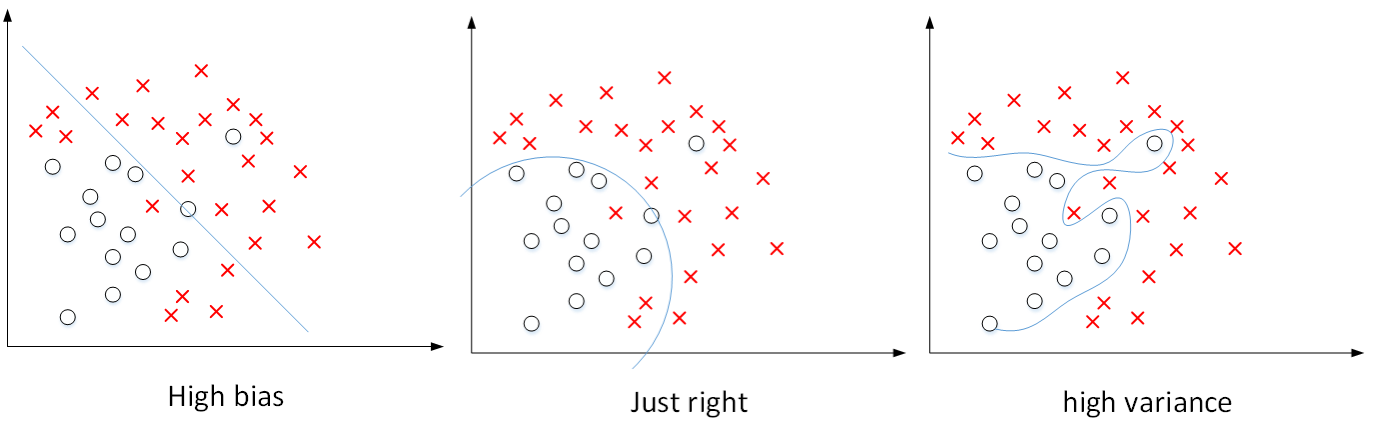
* Bias / Variance 偏差、方差Vanishing and Exploding gradients 梯度消失 和 梯度爆炸
* High Bias偏差是对应着欠拟合，就是拟合的效果太差了，离想要的效果差的太多了。
* High Variance 高方差是对应着过拟合，就是拟合度太高了，有一些需要舍弃掉的点都考虑到了
* 
* 对于神经网络
* 如果训练集的错误比较低，验证集的错误比较高，那么就是说过拟合了
* 如果训练集和验证集的错误都差不多，那就是欠拟合了
* 如果训练集已经够差了，然后验证集更差了，那就是过拟合和欠拟合都存在
* 
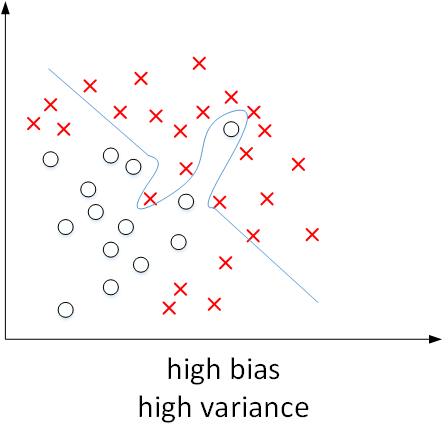
* 对于神经网络，避免欠拟合的方式是增加神经网络的隐藏层个数以及神经元个数从而延长训练时间。避免过拟合的方式是增加训练样本数据，正则化等
* 正则化 Regulation
* 就是在机器学习中，对原始的损失函数引入额外的信息，可以防止过拟合，也可以提高模型泛化性能
* 在逻辑回归中，两种常用的Logistic Regression
* L2 regularization
* J(w,b)=1m∑i=1mL(y^(i),y(i))+λ2m∣∣w∣∣22J(w,b) = \\frac {1}{m} \\sum^m_{i=1} L(\\widehat y^{(i)}, y^{(i)}) + \\frac {\\lambda}{2m} ||w||^2_2J(w,b)=m1∑i=1mL(y(i),y(i))+2mλ∣∣w∣∣22
* ∣∣w∣∣22=∑j=1nxwj2=wTw||w||^2\_2 = \\sum^{n\_x} _{j=1} w^2_j = w^Tw∣∣w∣∣22=∑j=1nxwj2=wTw
* L1 regularization
* J(w,b)=1m∑i=1mL(y^(i),y(i)+λ2m∣∣w∣∣1J(w,b) = \\frac {1}{m} \\sum ^m _{i =1} L(\\widehat y^{(i)} ,y^{(i)} + \\frac {\\lambda}{2m} ||w||_1J(w,b)=m1∑i=1mL(y(i),y(i)+2mλ∣∣w∣∣1
* ∣∣w∣∣1=∑j=1nx∣wj∣||w||\_1 = \\sum ^{n\_x}_{j=1} |w_j|∣∣w∣∣1=∑j=1nx∣wj∣
* L1 正则化得到的W更加稀疏，就是很多的w为零；可以节省存储空间，但是由于L1在微分求导的方面更加复杂，所以L2更常用
* λ\\lambdaλ是正则化参数，可以设置不同的值，通过Dev set进行验证。
* 在深度学习中，L2被表达为
* J(w\[1\],b\[1\],..........,w\[L\],b\[L\]=1m∑i=1mL(y^(i),y(i))+λ2m∑i=1L∣∣w\[l\]∣∣2J(w^{\[1\]}, b^{\[1\]},.........., w^{\[L\]},b^{\[L\]} = \\frac {1}{m}\\sum ^m_{i=1} L(\\widehat y ^{(i)}, y^{(i)}) + \\frac {\\lambda}{2m} \\sum^L_{i=1} ||w^{\[l\]} ||^2J(w\[1\],b\[1\],..........,w\[L\],b\[L\]=m1∑i=1mL(y(i),y(i))+2mλ∑i=1L∣∣w\[l\]∣∣2
* ∣∣w\[l\]∣∣2=∑i=1nl∑n\[l−1\](wij\[l\])2||w^{\[l\]}||^2 = \\sum ^{n^{l}}_{i=1}\\sum ^{n\[l-1\]}(w^{\[l\]} _{ij})^2∣∣w\[l\]∣∣2=∑i=1nl∑n\[l−1\](wij\[l\])2 Frobenius范数，就是计算所有元素平方和再开方
* ∣∣A∣∣F=∑i=1m∑j=1n∣aij∣2||A||\_F = \\sqrt {\\sum ^m \_{i = 1} \\sum ^n _ {j=1} |a_{ij}|^2}∣∣A∣∣F=∑i=1m∑j=1n∣aij∣2
* 如果加入了正则化项，梯度下降的算法中的dwldw^{l} dwl要改变
* dw\[l\]=dwbefore\[l\]+λmw\[l\]dw^{\[l\]} = dw^{\[l\]}_{before} + \\frac {\\lambda}{m}w^{\[l\]}dw\[l\]=dwbefore\[l\]+mλw\[l\]
* w\[l\]:=w\[l\]−α∗dw\[l\]=w\[l\]−α∗(dwbefore\[l\]+λmw\[l\])=(1−αλm)w\[l\]−α∗dwbefore\[l\]w^{\[l\]} : = w^{\[l\]} - \\alpha * dw^{\[l\]} = w^{\[l\]} - \\alpha * (dw^{\[l\]}_{before} + \\frac {\\lambda}{m} w^{\[l\]}) = (1-\\alpha \\frac {\\lambda}{m}) w^{\[l\]} - \\alpha *dw^{\[l\]}_{before}w\[l\]:=w\[l\]−α∗dw\[l\]=w\[l\]−α∗(dwbefore\[l\]+mλw\[l\])=(1−αmλ)w\[l\]−α∗dwbefore\[l\]
* 其中，(1−αλm<1(1-\\alpha \\frac {\\lambda}{m} <1(1−αmλ<1
* 就是其实L2是最常用的
* 正则化为什么可以有效防止过拟合
* 当λ\\lambdaλ 很大的时候，w^{\[l\]} 约为0，就是这些神经元的作用就很小了忽略不计了；但是如果太大了，就被简化成逻辑回归模型了，就从过拟合变成欠拟合了
* Dropout Regularization
* 在深度学习网络的训练过程中，对于每层的神经元，按照一定的概率将其暂时从网络中丢弃，就是说，每次训练的时候，每一层都有部分的神经元不工作，可以减少工作做得神经元从而简化复杂的网络模型
* 
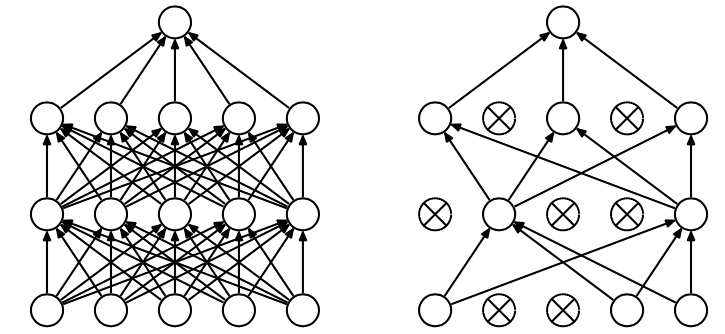
* 实现Dropout 的方法：
* Inverted dropout
* dl = np.random.rand(al.shape\[0\],al.shape\[1\])* Vanishing and Exploding gradients 梯度消失 和 梯度爆炸
* 就是在训练一个层数非常多的神经网络的时候，计算得到的梯度可能非常小也可能非常大
* 就是说，如预测输出是如图所示的样子，那么如果每层权重都大于一，那么就会数值爆炸，如果每层权重都小于一，就会数值消失
* 
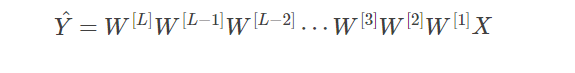
* 对权重w进行一些初始化处理 Weight Initialization
* 就是说，不同的激活函数对应着不同的初始化方法
* tanh,
* 
* ReLU
* 
* 梯度检查 Numerical approximation of gradients
* 可以验证反向传播过程中梯度下降算法是否正确
* 就是用这个简单的算法去近似计算函数在某点处的梯度值
* 
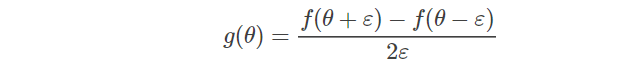
* 对于反向传播过程
* dθapprox\[i\]=J(θ1,θ2,..,θi+ε,....)−J(θ1,θ2,.....,θi−ε,.....)2εd\\theta _{approx} {\[i\]} = \\frac {J(\\theta\_1, \\theta\_2, ..,\\theta\_i + \\varepsilon,....) - J(\\theta\_1, \\theta\_2,.....,\\theta\_i - \\varepsilon,.....)}{2\\varepsilon}dθapprox\[i\]=2εJ(θ1,θ2,..,θi+ε,....)−J(θ1,θ2,.....,θi−ε,.....)
* 通过计算两者的欧氏距离来计算两者的相似度
* ∣∣dθapprox−dθ∣∣2∣∣dθapprox∣∣2+∣∣dθ∣∣2\\frac{||d\\theta_{approx} -d\\theta||\_2}{||d\\theta\_{approx||\_2 }+||d\\theta||\_2}∣∣dθapprox∣∣2+∣∣dθ∣∣2∣∣dθapprox−dθ∣∣2
* 就是如果这个欧式距离小，就是两者接近计算正确，如果较大就出问题了得修bug
* 梯度检查不应该在整个过程中都是用，只能在debug的时候使用；检查的时候应该包括正则化，但是应该关闭dropout
* Mini-batch gradient descent 迷你batch 梯度下降
* 就是把m个训练样本分成一堆子集，每一个都是mini-batches，这样每个数据子集的包含的数据量变小，速度就会大大提高。
* 一些符号字母：
* X(i)X^{(i)}X(i) 第iii个样本
* Z\[l\]Z^{\[l\]}Z\[l\]：神经网络第lll层网络的输出
* Xt,Yt:X^{t}, Y^{t}:Xt,Yt: 第ttt组mini-batch
* 具体实施的时候，就是对每个子集挨个轮询
* 
* 所有m个训练样本都进行了一次梯度下降计算，轮一次就是一个epoch，每次epoch，都将所有的总体训练数据重新打乱
* 对于mini batch 的一些更深层次的理解：
* 如下图，就是左边是所有的整体一批出了，右边的是一组一组一组一组的去挨个做的；min-batch这种，是震荡下降的，是因为不同的子集之间的情况有所不同，有可能有的有噪声noise
* 
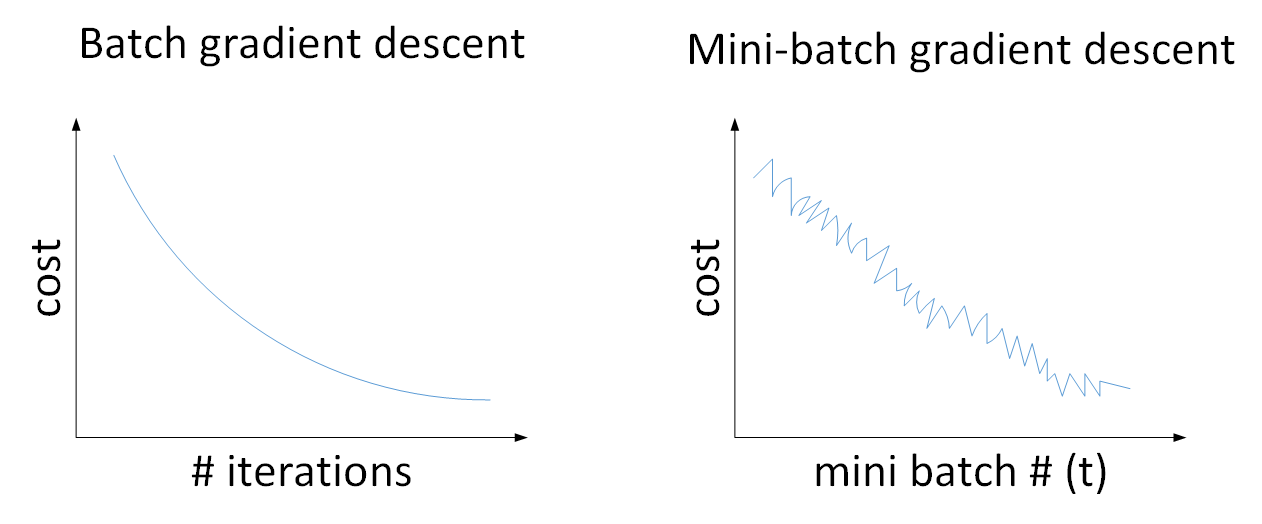
* 如果 m<= 2000，一般直接用Batch gradient descent，就是直接不分组全部都放一块做了；如果m很大的话就要分组，按照64，128这种分组方式分，弄成2的幂
* Exponentially weighted averages 指数加权平均
* 这种可以看到整体的数据变化趋势，也叫滑动平均算法，形式如下：
* Vt=βVt−1+(1−β)θtV\_t = \\beta V\_{t-1} + (1 - \\beta) \\theta _ tVt=βVt−1+(1−β)θt 这里的 θ\\thetaθ指的是原始数据
* 一般形式：
* Vt=βVt−1+(1−β)θt=(1−β)θt+(1−β)∗β∗θt−1+(1−β)∗β2∗θt−2+...+(1−β)∗βt−1∗θ1+βt∗V0V\_t = \\beta V\_{t-1} + (1-\\beta )\\theta\_t =(1-\\beta )\\theta\_t + (1-\\beta ) * \\beta * \\theta_{t-1} + (1-\\beta)*\\beta ^2 *\\theta_{t-2} + ...+(1-\\beta) * \\beta ^{t-1} * \\theta\_1 + \\beta ^t * V\_0Vt=βVt−1+(1−β)θt=(1−β)θt+(1−β)∗β∗θt−1+(1−β)∗β2∗θt−2+...+(1−β)∗βt−1∗θ1+βt∗V0
* 比如，下图是伦敦半年内的气温变化，但是这个数据是有抖动的，而且抖动比较大，就需要处理一下
* 
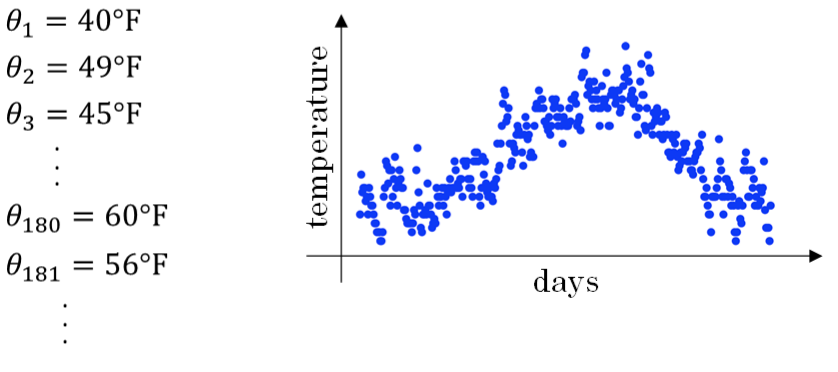
* 通过上面这个指数加权平均算法，得到的最终数据
* 
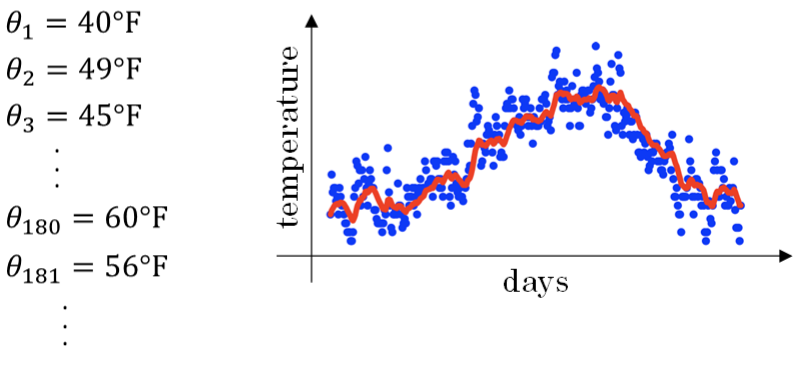
* 这里的β\\beta β取值为0.9, 那么， 11−β=10\\frac{1}{1-\\beta} = 101−β1=10 就是表示取前十天加权平均
* Bias correction偏移修正
* 每次计算完VtV_tVt之后，进行如下处理：
* Vt=Vt1−βtV\_t = \\frac {V\_t}{1 - \\beta ^t}Vt=1−βtVt
* Gradient descent with momentum 动量梯度下降算法
* 就是在每次训练时，对梯度进行指数加权平均处理，然后用得到的梯度值进行权重W和常数项B的更新，表达式如下：
* VdW=β∗VdW+(1−β)∗dWV_{dW} = \\beta * V_{dW} + (1-\\beta ) * dWVdW=β∗VdW+(1−β)∗dW
* Vdb=β∗Vdb+(1−β)∗dbV_{db} = \\beta \*V_{db} + (1-\\beta) \* dbVdb=β∗Vdb+(1−β)∗db
* W=W−αVdW,b=b−αVdbW = W - \\alpha V_{dW} , b = b - \\alpha V_{db}W=W−αVdW,b=b−αVdb
* 一般β取0.9
* RMSprop算法
* 这是一种新的优化梯度下降速度的算法
* SW=βSdW+(1−β)dW2,Sb=βSdb+(1−β)db2S\_W = \\beta S\_{dW } + (1-\\beta) dW^2, S\_b = \\beta S\_{db} + (1-\\beta)db^2SW=βSdW+(1−β)dW2,Sb=βSdb+(1−β)db2
* W:=W−αdWSW+ϵ,b:=b−αdbSb+ϵW := W - \\alpha \\frac{dW}{\\sqrt{S\_W + \\epsilon }},b:= b-\\alpha \\frac{db}{\\sqrt{S\_b +\\epsilon}}W:=W−αSW+ϵdW,b:=b−αSb+ϵdb
* 这里的ϵ\\epsilonϵ是一个极小的常熟，用来避免分母为0
* Adam optimization algorithm Adam 算法
* 这种算法结合了动量梯度下降算法 和RMSprop算法的优势，流程如下
* 如图所示，就是把两种算法分别结合了起来，两个内容加在一起就是这种算法了
* 
* Learning rate decay
* 减小学习因子α\\alphaα可以有效提高训练速度
* 就是对于这个α\\alphaα 也不断地改变，在不断地变小；就是还没逼近最优解的时候步长大一些，慢慢逼近，然后快到了之后慢慢前进，步长减小，慢慢微弱逼近最优值
* α=11+decay_rate∗epochα0\\alpha = \\frac{1}{1+decay\\\_rate * epoch} \\alpha\_0α=1+decay_rate∗epoch1α0
* 这里的decay_rate是参数，可以调整的，然后epoch是训练的次数，就是你每多训练一次，epoch都会增加，α\\alphaα会不断变小
* 几个其他的可选的计算公式：
* α=kepoch∗a0\\alpha = \\frac{k}{\\sqrt{epoch}} * a_0α=epochk∗a0
* k是可调参数
* α=0.95epoch∗α0\\alpha = 0.95^{epoch} * \\alpha_0α=0.95epoch∗α0
* α=kt∗α0\\alpha = \\frac{k}{\\sqrt{t}} * \\alpha_0α=tk∗α0
* t是mini - batch number
* The problem of local optima
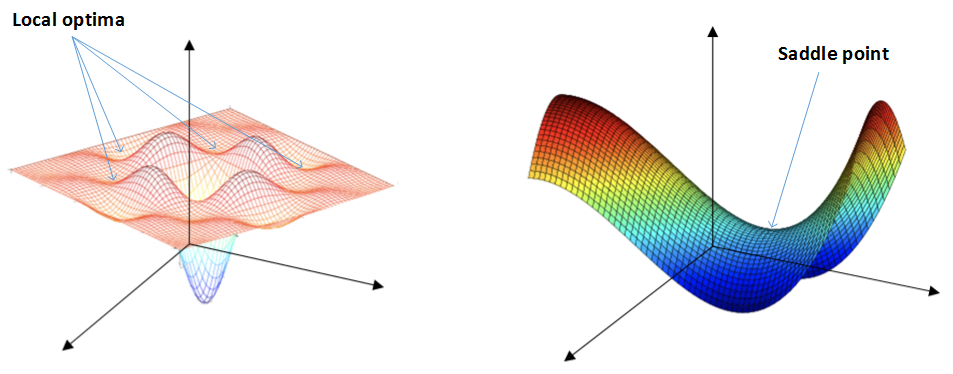
* 对于神经网络，local optima 局部最优解是右边这种马鞍状的，他会降低神经网络学习速度，就是在马鞍上的时候梯度很小，前进缓慢
* 
* Tuning Process 调整超参数
* 深度学习需要调试的超参数有很多，如下：
* α\\alphaα ：学习因子
* β\\betaβ ：动量梯度下降因子
* β1,β2,ϵ\\beta\_1, \\beta\_2,\\epsilonβ1,β2,ϵ: Adam算法参数（一般设置为0.9，0.999，10−810^{-8}10−8）
* layers: 神经网络层数
* hidden units： 各隐藏层的神经元个数
* learning rate decay：学习因子下降参数
* mini-batch size：批量训练样本包含的样本个数
* 最重要的参数是学习因子α\\alphaα
* 调试参数
* 对于layers和hidden units，都是正整数层数，都是进行均匀随机采样
* 对于α,β\\alpha, \\betaα,β这些， 需要使用非均匀随机采样，就是最佳的α值在【0.0001，0.1】之间，所以更关注这一区域才对，对于β，越接近1，指数加权平均的个数越多，变化越大，所以对于接近1的地方采集的应该更加密集
* Batch Norm Work 在神经网络中的作用
* 可以加快学习速度，均值为0，方差为1的规范化处理后；还可以让神经网络的权重W的更新更加稳健，前面的W的变化对后面的W造成的影响很小，更加健壮
* Softmax 回归模型
* 之前学的神经网络都是二分类问题，就是神经网络输出层只有一个神经元，依靠是否大于零点五来判断类别，如果是多分类问题，就是有很多个输出种类，
* 激活函数如下：
* z\[L\]=W\[L\]a\[L−1\]+b\[L\]z^{\[L\]} = W^{\[L\]}a^{\[L-1\]} + b^{\[L\]}z\[L\]=W\[L\]a\[L−1\]+b\[L\]
* ai\[L\]=ezi\[L\]∑i=1Cezi\[L\]a\_i^{\[L\]} = \\frac{e^{z\_i^{\[L\]}}}{\\sum_{i=1}^C e^{z_i^{\[L\]}}}ai\[L\]=∑i=1Cezi\[L\]ezi\[L\]
* 输出层每个神经元的输出
* ∑i=1Cai\[L\]=1\\sum _{i=1}^Ca_i^{\[L\]} = 1∑i=1Cai\[L\]=1
* 对于m个训练样本，最终的结果与二元分类的结果是一致的
* dZ\[L\]=A\[L\]−YdZ^{\[L\]} = A^{\[L\]} - YdZ\[L\]=A\[L\]−Y
* TensorFlow
* 吴恩达视频相关的 TensorFlow 理论基础已经掌握，等吴恩达视频助学金批下来再上代码
* 就是一个框架，跟springboot一样掌握就好
-
机器学习策略和方法
-
Orthogonaloizatin正交化
- 正交化方法，就是每次只调试一个参数，其他的参数保持不变，得到的模型某一个性能改变其他的不变
-
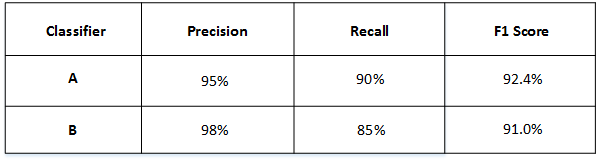
Single number evaluation metric 单值评价指标
-
F1 Score：
- F1=2∗P∗RP+RF1 = \frac{2*P*R}{P+R}F1=P+R2∗P∗R
-
比如，如下所示的两个模型，他们的两个指标准确率和召回率如图
-
-
通过公式计算，结果如下，选A
-
-
平均值有时候也可以作为评价指标
-
-
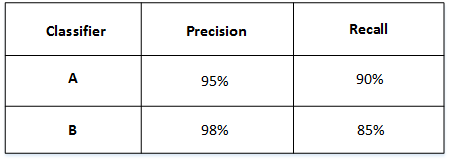
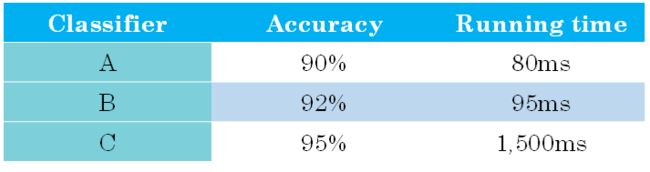
Satisficing (优化指标) and Optimizing metic（满意指标）
-
如图所示，有运行时间和准确率两种指标
-
-
这时候就可以把运行时间设置为满意指标，准确率设置成优化指标；就是说，给运行时间设置一个阈值，要求运行时间在必须达到阈值的情况下，选择准确率最好的；概括来说，性能指标 Optimizing metic）是需要优化的，越优越好；而满意指标（Satisficing metic）只要满足设定的阈值就好了。
-
-
Train/dev/test distributions
- dev test 和 test sets 应该来源于同一分布，并且都反映了实际样本的情况，否则表现就不会很好
-
什么时候改变dev/test sets 和metrics
-
有时候可以修改评价指标和体系来增加某种类型的代价
-
如：
-
比如A和B两种模型，A的错误率更低但是，A 可以通过色情图片，这个是不能接受的，所以虽然B差点准确率，但是更喜欢B
-
但是我们可以改cost function来增加色情图片的代价
-
-
-
机器学习的理念就是，第一步找靶心，第二步是通过训练射中靶心
-
-
机器学习经过训练会不断地接近human-level performance，但是超过这条线之后，准确性会上升地比较缓慢， 最终不断接近理想的最优情况，称之为bayes optimal error，也就是理论上所有模型都不会超过的这条线，也是最佳表现
-
Avoidable bias
-
把training error和human-level error之间的差值称为bias，也叫avoidable bias，dev error和training error之间的差值称为variance，根据两者之间的相对大小可以知道算法的欠拟合 or 过拟合
-
当算法模型的表现超过human - level performance的时候，很难通过人的直觉来解决如何提高算法模型性能的问题
-
-
Carrying out error analysis 错误分析
- 简言之就是，比例越大，影响越大，月应该花费时间和精力着重解决这一问题，可以使得改进模型更加有针对性，更提高效率
-
Cleaning up incorrectly labeled data
-
在监督式学习会出现输出y标注错误；如果label标错是偶然事件，那么鲁棒性比较好无需修复，如果是系统的问题，那么就会产生影响
-
如果Errors due incorrect labels占dev set error的占比很小，比如dev error：10%， incorrect labels error：0.6%这种，就可以忽略不计incorrect labels error
-
如果占比很大，比如dev set error 2%，incorrect labels 0.6%，这种占比非常非常大的，就需要一定要手动修正
-
-
构建机器学习应用模型的方法：
- 先快速构建第一个简单模型然后反复迭代优化
-
当Training and test set 来自不同的分布。如何解决：
-
举例：
-
猫类识别的时候，如果train set 来自网络下载图片清晰，dev和test set 都来自用户手机拍摄，比较模糊；并且两者的大小不一
-
-
第一种方法：
-
将train set 和dev/test set完全混合，然后随机选择一部分作为train和devset
-
优点：train set和 dev / test set 分布一致
-
缺点：dev/test set 中的web pages占比太大，并不能验证
-
不是很好的方式
-
-
-
第二种方式
-
将原来的train set 和一部分的dev/test set 组合成train set， 剩下的dev/test set 分别作为 dev set 和 test set；
-
这种比较常用，性能表现比较好，就是都能满足
-
-
-
Bias and Variance with mismatched data distributions
-
如果训练的数据集和测试的数据集是不同分布的，那么无法直接根据相对值的大小来判断；就比如，训练集的错误和测试集的错误是来自算法本身，或者就是单纯的dev set都质量太差了不能用
-
train set 和 dev/test set分布不一致的情况下，定位是否出现variance的方法：
-
设置train - dev set.就是，从train set 中抽离一部分出来作为 train - dev set，不作为训练模型使用，而是用于验证
-
设置完了之后，如果training - dev error和 training error 的差距过大，就是variance 过大，否则就是样本的问题
-
-
-
-
Addressing data mismatch
- 为了解决train set 和 dev /test set 分布不一致的问题，可以进行人工数据合成，就是比如如果训练的样本太过干净了，就人工添加背景噪声等等；但是这样可能会产生过的效果，需要注意
-
Transfer learning 迁移学习
-
可以将已经训练好的模型的一部分知识直接应用到另一个类似的模型里去
-
也就是说，只需要更换权重系数W[L],b[L]W{[L]},b{[L]}W[L],b[L]’
-
迁移学习就是保留原神经网络的一部分，再添加新的网络层；就是有的层是类似的比如说提取图片的边缘和曲线等等
-
-
Multi-task learning 多任务学习
-
就是构建神经网络的同时执行多个任务，就类似将多个神经网络融合在一起，如果任务有C个输出，那么输出y的维度是(C, 1)。比如汽车自动驾驶中，需要实现的多任务是行人，车辆，交通标志和呃信号灯，如果检测出汽车和交通标志，那么y就是
- y=[0110]y = \begin{bmatrix}0\\1\\1\\0\end{bmatrix}y=⎣⎢⎢⎢⎡0110⎦⎥⎥⎥⎤
-
多任务学习模型的 cost function
- 1m∑i=1m∑j=1cL(y^j(i),yj(i))\frac{1}{m} \summ_{i=1}\sumc_{j=1}L(\widehat y ^{(i)}_j, y_j^{(i)})m1∑i=1m∑j=1cL(yj(i),yj(i))
-
多任务学习模型的Loss Function
- L(yj(i),yj(i))=−yj(i)logyj(i)−(1−yj(i))log(1−y(i))L(\widehat y_j{(i)},y{(i)}_j) = -y_j^{(i)}log\widehat y_j^{(i)} - (1-y_j{(i)})log(1-y{(i)})L(yj(i),yj(i))=−yj(i)logyj(i)−(1−yj(i))log(1−y(i))
-
相对来讲，迁移学习用的更多
-
-
End to End deep learning 端到端深度学习
-
将所有的不同阶段的数据处理系统或学习系统模块组合在一起，用一个单一的神经网络模型来实现所有的功能，只关心输入和输出
-
优点
-
可以让该数据说话
-
可以减少所需部件的手工设计
-
-
缺点
-
需要更多的数据
-
没法搞手工设计了
-
-
-
* 卷积神经网络基础
* Computer Vision 深度学习应用的主要方向
* 主要问题：
* Image Classification 图像分类
* Object detection目标检测
* Neural Style Transfer 神经风格转换
* 
* 主要问题
* 输入层维度很大，比如64\*64 \*3的图片，输入层的维度12288，会导致所需的内存、计算量较大
* Edge Detection Example
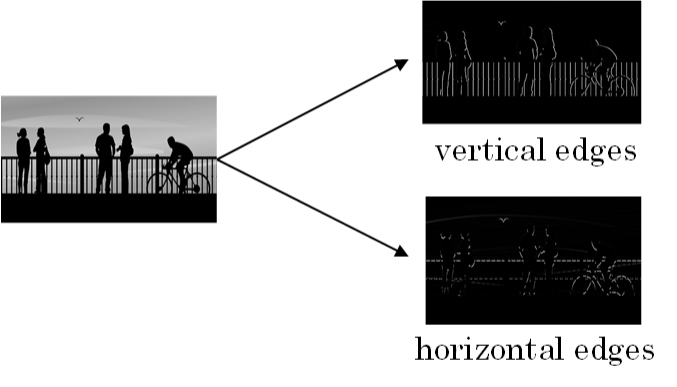
* 两种图片边缘：
* 垂直边缘 Vertical edges
* 水平边缘 Horizontal Edges
* 
* 卷积： Convolution
* [https://www.zhihu.com/question/22298352](https://www.zhihu.com/question/22298352)
* 通过两个函数f和g生成第三个函数的一种数学算子，是一种积分变化的数学方法
* 函数f,gf,gf,g的卷积 f∗g(n)f*g(n)f∗g(n)如下：
* (f∗g)(n)=∫−∞∞f(γ)g(n−γ)dγ(f*g)(n) = \\int _{-\\infty}^{\\infty}f(\\gamma) g(n-\\gamma)d\\gamma(f∗g)(n)=∫−∞∞f(γ)g(n−γ)dγ
* 先对g函数进行反转，就是在数轴上把g函数从右边褶到左边去，这就是卷积的“卷”的由来
* 再把g函数平移到n，在这个位置对两个函数的对应点进行相乘再相加，就是“积”的过程
* 图像处理中的卷积
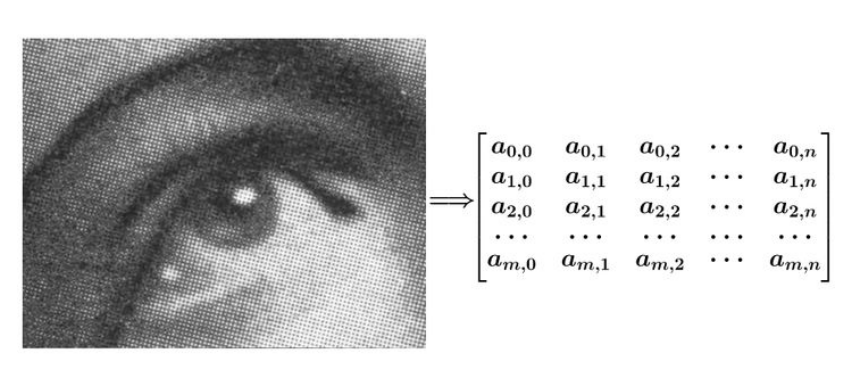
* 图像可以表示为矩阵的形式
* 
* 对图像的处理函数（如平滑，或者边缘提取处理）可以用一个g矩阵来表示
* 
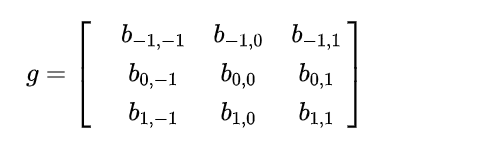
* 图片的边缘检测
* 可以通过特定的滤波器进行卷积来实现；如图所示，就是一种卷积
* 
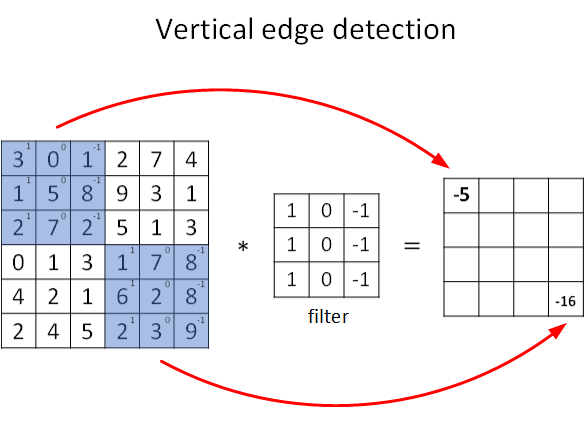
* “*”表示卷积操作
* python 里的卷积用conv_forward()
* tensorflow里的卷积用tf.nn.conv2d()
* keras，卷积用Conv2D()
* 图片的边缘有两种渐变方式，一种是由明变暗，一种是由暗变明
* 两种滤波器算子
* Horizontal 水平边缘检测的滤波器算子
* 111000−1−1−1\\begin{matrix} 1&1&1\\\0&0&0\\\-1&-1&-1\\end{matrix}10−110−110−1
* 
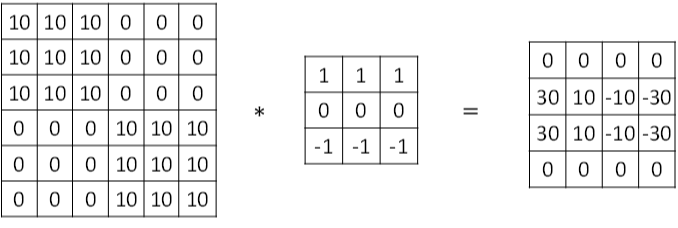
* vertical 垂直边缘检测的滤波器算子：
* 10−110−110−1\\begin{matrix}1&0&-1\\\1&0&-1\\\1&0&-1\\end{matrix}111000−1−1−1
* 还有很多种常见的滤波器管道，如图所示，作用是增加图片中心权重
* 
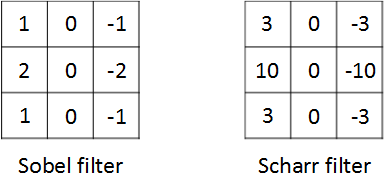
* 如果想检测图片的各种边缘特征，不仅限于垂直边缘和水平边缘，那么filter的数值一般需要通过模型训练得到;CNN的主要目的就是计算这些filter的数值
* Padding
* 图片卷积会有问题，就是经过卷积的图片尺寸会变小，图片边缘的信息丢失
* 解决方式
* 就是padding扩展，把原始的图片进行扩展，扩展的区域补零
* 
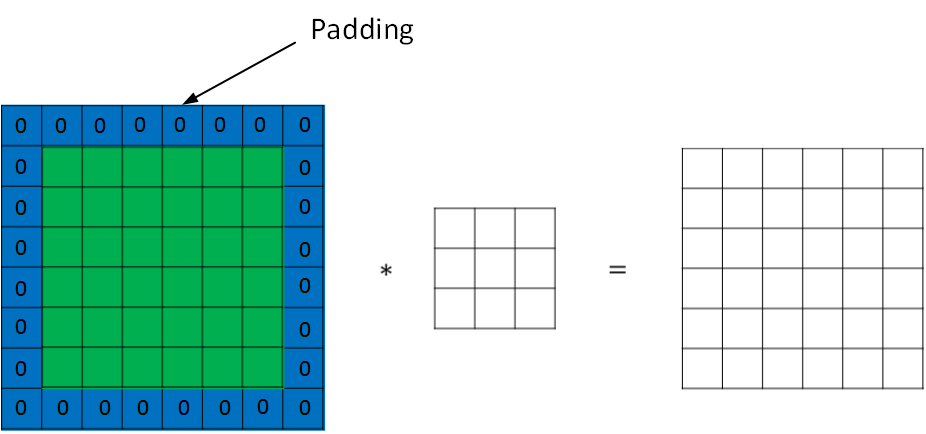
* padding的成果：
* 原始图片尺寸：n∗nn*nn∗n
* filter算子的尺寸是f∗ff*ff∗f
* 正常算法的卷积后的图片尺寸是：(n−f+1)∗(n−f+1)(n-f+1) * (n-f+1)(n−f+1)∗(n−f+1)，这其中的fff一般为奇数
* 经过padding之后，原始的图片尺寸变为：
* (n+2p)∗(n+2p)(n+2p) * (n+2p)(n+2p)∗(n+2p)
* filter:f∗ffilter: f*ffilter:f∗f
* 卷积后的图片尺寸为(n+2p−f+1)∗(n=2p−f+1)(n+2p-f+1)*(n=2p-f+1)(n+2p−f+1)∗(n=2p−f+1)
* p=f−12p = \\frac{f-1}{2}p=2f−1就可以保证图片尺寸不变了
* 如果没有padding 操作，那么就是valid convolutions；如果有了padding操作，那么就是Same Convolutions
* Stride Convolutions
* stride 表示filter在原图片中水平方向和垂直方向每次的步进长度
* 一般默认stride 为 1， 如果stride = 2，那么表示filter的每次步进长度为2，每隔一点移动一次
* 关于步长的解读如下网址：
* [https://blog.csdn.net/weixin_38279101/article/details/103820166#:~:text=%E5%8D%B7%E7%A7%AF%E6%AD%A5%E9%95%BF%20%E4%B9%9F%E5%8F%AB%20%E5%8D%B7%E7%A7%AF%20%E6%AD%A5%E5%B9%85%EF%BC%8C%E8%8B%B1%E6%96%87%E5%90%8D%E5%AD%97%E6%98%AFstride%EF%BC%8C%E4%BB%A3%E8%A1%A8%E6%BB%A4%E6%B3%A2%E5%99%A8%E6%AF%8F%E7%A7%BB%E5%8A%A8%E4%B8%80%E6%AC%A1%E7%A7%BB%E5%8A%A8%E7%9A%84%E6%AD%A5%E5%B9%85%EF%BC%8Cs%3D2%E5%88%99%E6%BB%A4%E6%B3%A2%E5%99%A8%E6%AF%8F%E6%AC%A1%E7%A7%BB%E5%8A%A82%E6%A0%BC%E3%80%82%20%E4%B8%BE%E4%BE%8B%EF%BC%9A%20,%20%20Wu%E6%95%99%E6%8E%88%E7%9A%84%E6%96%B9%E7%A8%8B%E8%A1%A8%E8%BE%BE%E5%BC%8F%20%E5%8D%B7%E7%A7%AF%20%E5%90%8E%E5%9B%BE%E7%89%87%E8%BE%B9%E9%95%BF%3D%20%28%20%28n%2B2p-f%29%2Fs%29%2B1](https://blog.csdn.net/weixin_38279101/article/details/103820166#:~:text=%E5%8D%B7%E7%A7%AF%E6%AD%A5%E9%95%BF%20%E4%B9%9F%E5%8F%AB%20%E5%8D%B7%E7%A7%AF%20%E6%AD%A5%E5%B9%85%EF%BC%8C%E8%8B%B1%E6%96%87%E5%90%8D%E5%AD%97%E6%98%AFstride%EF%BC%8C%E4%BB%A3%E8%A1%A8%E6%BB%A4%E6%B3%A2%E5%99%A8%E6%AF%8F%E7%A7%BB%E5%8A%A8%E4%B8%80%E6%AC%A1%E7%A7%BB%E5%8A%A8%E7%9A%84%E6%AD%A5%E5%B9%85%EF%BC%8Cs%3D2%E5%88%99%E6%BB%A4%E6%B3%A2%E5%99%A8%E6%AF%8F%E6%AC%A1%E7%A7%BB%E5%8A%A82%E6%A0%BC%E3%80%82%20%E4%B8%BE%E4%BE%8B%EF%BC%9A%20,%20%20Wu%E6%95%99%E6%8E%88%E7%9A%84%E6%96%B9%E7%A8%8B%E8%A1%A8%E8%BE%BE%E5%BC%8F%20%E5%8D%B7%E7%A7%AF%20%E5%90%8E%E5%9B%BE%E7%89%87%E8%BE%B9%E9%95%BF%3D%20%28%20%28n%2B2p-f%29%2Fs%29%2B1)
* 卷积后的图片尺寸为：
* 
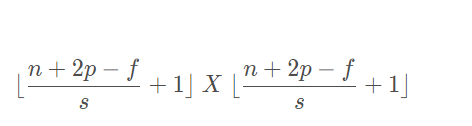
* 就是说要通过这种方法来保证卷积不会改变图片尺寸
* Convolutions Over Volume
* RGB图片是三通道的，其对应的滤波器算子也是三通道的，分别表示高度、宽度和通道
* 计算方式：三个通道每个都单独跟对应的滤波器进行运算，然后三个通道的和相加，得到输出的像素值
* 可以通过设置多个滤波器组来实现多个内容检测，比如一组检测垂直边缘，一组检测水平边缘
* 卷积神经网络的单层结构：
* 如图所示，多了激活函数ReLU和偏移量b。就是输入的内容，先进行卷积操作，卷积操作的结果通过Relu 函数进行修正之后输出；CNN的优势在于，图片尺寸不会影响
* 
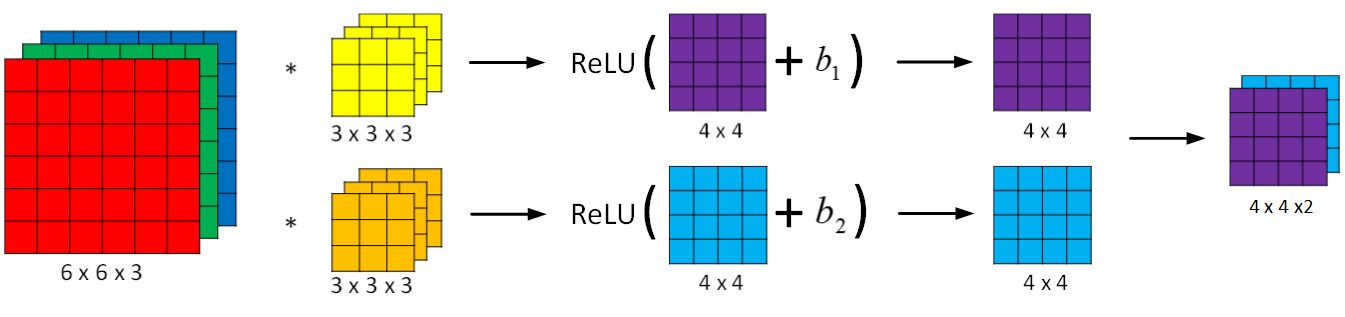
* Z\[l\]=WlA\[l−1\]+bZ^{\[l\]} = W^{l}A^{\[l-1\] } + bZ\[l\]=WlA\[l−1\]+b
* A\[l\]=g\[l\](Z\[l\])A^{\[l\]} = g^{\[l\]}(Z^{\[l\]})A\[l\]=g\[l\](Z\[l\])
* fl=filtersizef^{l} = filter\ sizefl=filtersize 滤波器尺寸
* p\[l\]=paddingp^{\[l\]} = paddingp\[l\]=padding 卷积
* sl=strides^{l} = stridesl=stride 步长
* nc\[l\]=numberoffiltersn_c^{\[l\]} = number\ of \ filtersnc\[l\]=numberoffilters
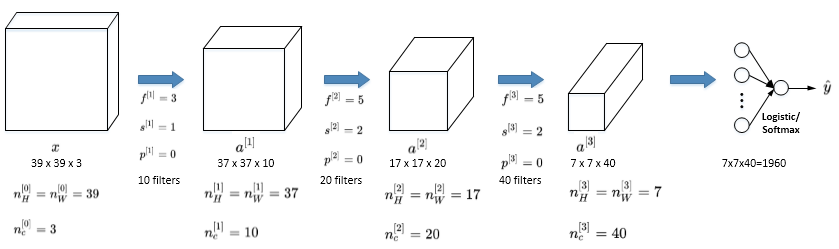
* Simple Convolutional Network Example 一个简单的CNN网络模型
* 大概是如图所示这个样子，就也是一层层的样子
* 
* CNN的三层
* Convolution
* Pooling
* Fully connected
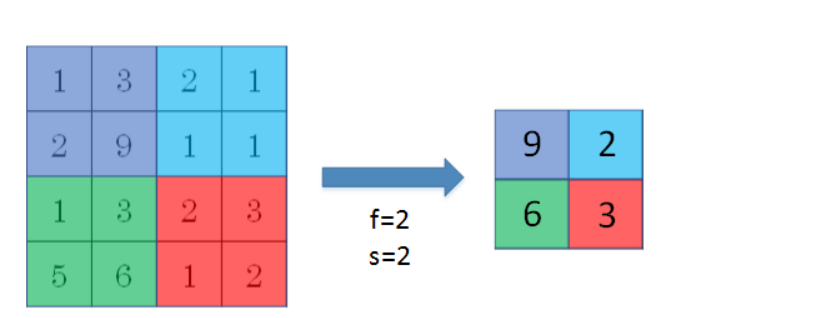
* Pooling layers
* 是CNN中用来减小尺寸，提高运算速度的，同样能减小noise的影响，让各特征值更具有健壮性
* 做法就是，在滤波器算子滑动区域内取最大值，就是max pooling，就像这样，只保留最大值
* 
* CNN的优势：
* 参数数目少的多
* 参数是共享的，并且连接时稀疏的，每一层的输出只与输入有关
* 深度卷积模型：案例研究
* 典型的CNN模型包括：
* LeNet-5
* AlexNet
* VGG
* 上代码
-
写代码遇到的
-
优化器 Optimizer
- https://ptorch.com/news/54.html
-
后记
以上为进行深度学习基础上的学习时笔记的全部内容，后续为进行具体项目的内容，转为更新论文专栏