深度学习中的normalization
背景：
normalization的作用：解决数据尺度分布异常的问题。relu可以解决，但可能出现梯度爆炸或消失。sigmoid也会导致梯度爆炸或消失。normalization则将数据尺度控制在一个合理区间内，主要是让梯度在0.5附近，不会过于接近0（消失），也不会超过1（爆炸）。
一、batch normalization
一个Batch的图像数据shape为[样本数N, 通道数C, 高度H, 宽度W]，将其最后两个维度flatten，得到的是[N, C, H*W]，标准的Batch Normalization就是在通道Channel这个维度上进行移动，对所有样本的所有值求均值和方差，所以有几个通道，得到的就是几个均值和方差。
批：一批数据，通常为mini-batch
标准化：0均值，1方差
优点：
- 可以用更大学习率，加速模型收敛
-
- 可以不用精心设计权值初始化
-
- 可以不用dropout或较小的dropout
-
- 可以不用L2或者较小的weight decay
-
- 可以不用LRN(local response normalization)——《 Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》这篇论文中提到
- 可以不用LRN(local response normalization)——《 Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》这篇论文中提到
参数：
• num_features：一个样本特征数量（最重要）
• e p s：分母修正项，默认10的-5次方
• momentum：指数加权平均估计当前mean/var，默认0.1
• affine：是否需要affine transform，默认为true
• track_running_stats：是训练状态，还是测试状态，默认为true，训练状态
主要属性：
• running_mean：均值
• running_var：方差
• weight：affine transform中的gamma
• bias： affine transform中的beta
注意事项：
训练：均值和方差采用指数加权平均计算
测试：当前统计值
running_mean = (1 - momentum) * pre_running_mean + momentum * mean_t
running_var = (1 - momentum) * pre_running_var + momentum * var_t
__init__(self, num_features, eps=1e-5, momentum=0.1, affine=True, track_running_stats=True)
关于样本、通道、特征：
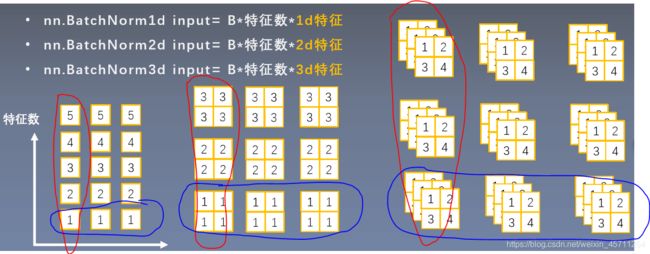
如上图，红色圈出来的为一个样本，一个样本有许多特征，每个特征有许多维度，对应着1-2-3维。BN是按照通道进行计算均值和方差。
gama和beta是可以学习的参数。
训练和测试时采取不同的均值方差计算方式。
二、LN
- Layer Normalization 起因：BN不适用于变长的网络，如RNN 思路：逐层计算均值和方差
注意事项：
2. 不再有running_mean和running_var，也就没有momentum - gamma和beta为逐元素的
- 主要参数：
• normalized_shape：该层特征形状
• eps：分母修正项
• elementwise_affine：是否需要affine transform，默认维true
nn.LayerNorm( normalized_shape, eps=1e-05, elementwise_affine=True)
Layer Normalization是在实例即样本N的维度上滑动，对每个样本的所有通道的所有值求均值和方差，所以一个Batch有几个样本实例，得到的就是几个均值和方差。
三、IN
Instance Normalization 起因：BN在图像生成（Image Generation）中不适用
思路：逐Instance（channel）计算均值和方
主要参数：
• num_features：一个样本特征数量（最重要）
• eps：分母修正项
• momentum：指数加权平均估计当前mean/var
• affine：是否需要affine transform
• track_running_stats：是训练状态，还是测试状 态
nn.InstanceNorm2d( num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
Instance Normalization是在样本N和通道C两个维度上滑动，对Batch中的N个样本里的每个样本n，和C个通道里的每个样本c，其组合[n, c]求对应的所有值的均值和方差，所以得到的是N⋅C N\cdot CN⋅C个均值和方差。
四、GN
Group Normalization 起因：小batch样本中，BN估计的值不准 思路：数据不够，通道来凑
注意事项：
- 不再有running_mean和running_var
- gamma和beta为逐通道（channel）的
应用场景：大模型（小batch size）任务
nn.GroupNorm 主要参数：
• num_groups：分组数
• num_channels：通道数（特征数）
• eps：分母修正项
• affine：是否需要affine transform
nn.GroupNorm( num_groups, num_channels, eps=1e-05, affine=True)
关于GN，多说两句，affine值默认为true，并且默认weight为一维的张量，值均为1，size对应通道数（每一个通道对应样本的一个特征，一个样本可以有好多特征），就是逐通道进行归一化。bias默认为0，size同上。下图是调试的结果：
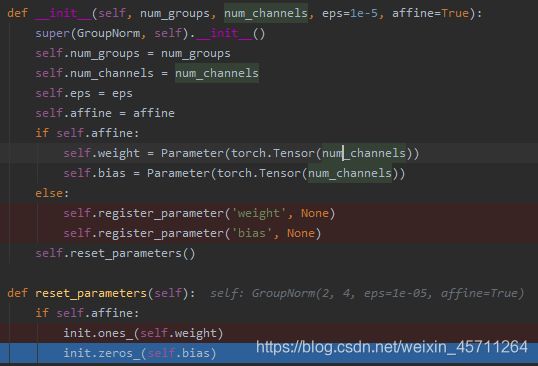
首先判断affine是否为true。若为true，则通过Parameter创建全零的张量，然后在通过reset_parameters方法进行赋值。
最后上一张图，直观理解四种归一化方法：
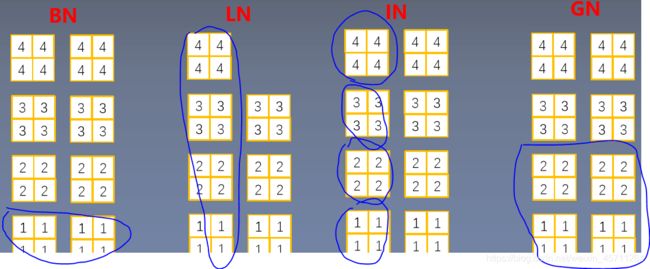
图中的蓝色圈出来的部分，就是各种归一化方法计算的基本单元。BN是一个通道，LN是一层(可以理解维一个样本的所有特征)，IN是单个特征，GN是在batchsize比较小的情况下，用通道数凑样本数的方法，简单理解就是将多个通道合并成一个组进行计算，增加数据量，提高计算结果的准确性和代表性。
总体来说，四种归一化方法，计算的思路都是一样的，都是“加减乘除”四步法，只是计算均值和方法的方法不同，若果考虑之前状态均值和方差的影响，则有动量momentum这个参数，训练和测试的状态要区分。
加减乘除个四步法如下：
训练状态切换，训练时用 net.train()，测试时用net.eval()，注意他们都是在同一个大循环里for epoch in range(MAX_EPOCH):
for epoch in range(MAX_EPOCH):
loss_mean = 0.
correct = 0.
total = 0.
net.train()
for i, data in enumerate(train_loader):
iter_count += 1
# forward
inputs, labels = data
outputs = net(inputs)
# backward
optimizer.zero_grad()
loss = criterion(outputs, labels)
loss.backward()
# update weights
optimizer.step()
# 统计分类情况
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).squeeze().sum().numpy()
# 打印训练信息
loss_mean += loss.item()
train_curve.append(loss.item())
if (i+1) % log_interval == 0:
loss_mean = loss_mean / log_interval
print("Training:Epoch[{:0>3}/{:0>3}] Iteration[{:0>3}/{:0>3}] Loss: {:.4f} Acc:{:.2%}".format(
epoch, MAX_EPOCH, i+1, len(train_loader), loss_mean, correct / total))
loss_mean = 0.
# 记录数据，保存于event file
writer.add_scalars("Loss", {"Train": loss.item()}, iter_count)
writer.add_scalars("Accuracy", {"Train": correct / total}, iter_count)
scheduler.step() # 更新学习率
# validate the model
if (epoch+1) % val_interval == 0:
correct_val = 0.
total_val = 0.
loss_val = 0.
net.eval()
最后注意各种方法的输入尺度：
BN:
self.conv1 = nn.Conv2d(3, 6, 5)
self.bn1 = nn.BatchNorm2d(num_features=6)
self.conv2 = nn.Conv2d(6, 16, 5)
self.bn2 = nn.BatchNorm2d(num_features=16)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.bn3 = nn.BatchNorm1d(num_features=120)
LN:
# feature_maps_bs shape is [8, 6, 3, 4], B * C * H * W
ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=True)
注：这里的输入只要是特征的后面几位都可以，比如634或者3*4或者4，如下：
batch_size = 2
num_features = 3
features_shape = (3, 4)
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0) # 4D
# feature_maps_bs shape is [8, 6, 3, 4], B * C * H * W
# ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=True)
# ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=False)
ln = nn.LayerNorm([3, 4])
# ln = nn.LayerNorm([6, 3])
output = ln(feature_maps_bs)
print("Layer Normalization")
print(ln.weight.shape)
print(feature_maps_bs[0, ...])
print(output[0, ...])
运行结果：
Layer Normalization
torch.Size([3, 4])
tensor([[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]],
[[2., 2., 2., 2.],
[2., 2., 2., 2.],
[2., 2., 2., 2.]],
[[3., 3., 3., 3.],
[3., 3., 3., 3.],
[3., 3., 3., 3.]]])
tensor([[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]],
[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]],
[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]]], grad_fn=<SelectBackward>)
IN:
instance_n = nn.InstanceNorm2d(num_features=num_features, momentum=momentum)
GN:
gn = nn.GroupNorm(num_groups, num_features)
归一化层一般在进入激活层之前。有时也用在线性层之前。