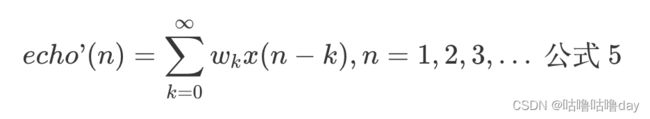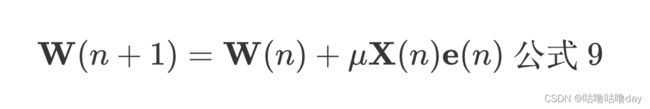07｜声学回声消除AEC（1）

目录

一. 回声产生的原因

 

二. 回声消除的基本原理

参考信号:

回声路径的传递函数：

 

三. 自适应滤波器

3.1 自适应滤波器适用的场景：

3.2 解决方案：

3.3 维纳滤波：

单讲：

维纳解

3.3 迭代计算算法：

3.3.1 LMS：

3.3.2 NLMS：

四. 线性滤波器的挑战和解决办法

4.1 延迟估计

4.2 双讲检测

双讲：

问题场景：

解决方案：

例子：

4.3 非线性

问题场景：

解决方案：

五. 小结

流程图如下：

思考题：

---

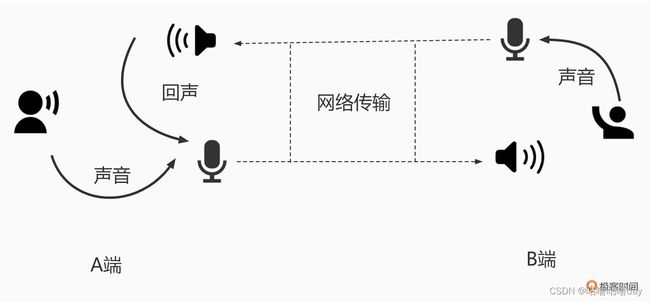
一. 回声产生的原因

如上图，回声简单的描述即 A端的麦克风接收到A端扬声器播出的来自B端的信号，回传给了B端。

当A端麦克风将 A端的人声与 回声混在一起后会显著降低语音的可懂度。需要使用AEC将回声消除后，只保留A端的音源声音发给B端。

 

二. 回声消除的基本原理

参考信号:

在近端收到的远端的声音信号叫做参考信号。

回声路径的传递函数：

经过扬声器播放、空气传播、房间墙体反射、麦克风采集后，参考信号不可避免的产生很多变换。 这个变换用数学的方式来表达叫做回声路径的传递函数。

如上图，近端信号除了回声还有近端语音。 echo(n)表示回声，y(n)表示近端声音。

z(n)=echo(n)+y(n) 

回声消除的目的是通过算法估计出回声路径的传递函数. f' 。如果估计的传递函数 f' 与真实的传递函数f是一致的。那么回声就可以完美消除了。

z’(n) = z(n) − f’(x(n))               公式 3

z’(n) = f(x(n)) − f' (x(n)) + y(n)     公式 4

z’(n) 表示近端信号， f' (x(n))估计出的传递函数，f(x(n))为真实的传递函数。

 

三. 自适应滤波器

采用实时更新的滤波器系数来模拟真实场景的回声路径。（回声路径建模）

3.1 自适应滤波器适用的场景：

复杂的声学场景：

实际AEC要面临复杂的、时变的声学环境。比如

1. 扬声器和麦克风说播放失真、采集失真会给声学信号带来很多非线性的变化。
2. 设备、系统调度的不稳定性可能造成回声和远端接受信号的延迟抖动。
3. 房间的混响、设备所处的位置的变化，都会带来回声路径的变化。

因此AEC必须快速的自适应算出这些回声路径的变化。如果估计不准，可能会导致回声泄漏或近端声音被压制，甚至造成丢字、卡顿等现象，严重影响实时音频互动的质量。

3.2 解决方案：

针对以上问题，经过半个多世纪的发展，摸索出一套以自适应滤波为基础的回声消除方法。

自适应滤波的核心思想：用实时更新的滤波器系数模拟真实场景的回声路径，然后结合远端信号估计出回声信号，再依从近端采集的混音信号去减去估计的回声，实现回声消除。

3.3 维纳滤波：

在一个相对稳定的声学环境中，回声路径中的延迟和房间的混响、音量的大小的变化等 都可以看作是对远端信号做的一系列线性变化。

这种线性变化可以用一个线性离散的FIR线性滤波器表示公式如下：

其中 wk​ 代表第 k 个滤波器系数。

单讲：

在近端只有回声信号没有近端信号，这种场景叫单讲。

回声信号的估计误差 e(n)  如下公式6:

e(n)=echo(n)−echo’(n) 公式 6

echo(n)表示原始的远端信号，echo’(n)表示对远端信号做的线性变化后的回声信号。

维纳解

维纳滤波就是以估计误差e(n) 的最小平方作为最优解的线性滤波器。（MSE）

如上，实时求这么大的矩阵的逆矩阵，算力无法支持。 这种直接求得的解叫维纳解，是全剧最优解，但计算量过大。

自适应滤波器的核心思想是面对回声路径不断变化的场景，比如移动电话等时，可以使用梯度下降法跌代的计算滤波器系数。

3.3 迭代计算算法：

包括LMS、和NLMS算法

3.3.1 LMS：

最小均方算法LMS（Least Mean Square）最早提出，也是最基础的自适应滤波方法。

基本原理如下：

W(n) 代表第n次迭代时滤波器的系数向量，X(n)是第n次迭代的输入向量(远端信号)，e(n)是第n次迭代的误差，u 是步长因子决定了滤波器系数的收敛速度，且u越大收敛越快。

梯度下降是SGD，不断逼近维纳解。 受输入向量(远端信号)X(n) 影响较大，如果远端信号音量小，从公式看到收敛速度会变很慢，反之梯度太大，会导致系数收敛过快。

3.3.2 NLMS：

通过X（n）的大小来动态调节步长因子，可以把X（n）类似归一化操作，如下图：

四. 线性滤波器的挑战和解决办法

除了采用NLMS方法还要解决三个问题：

1. 延迟估计
2. 双讲检测
3. 非线性

4.1 延迟估计

即回声延迟。

滤波器的感知长度：即X(n)输入信号的长度。

问题场景：

如果实际回声信号的传递路径过长，比如有很大的回声或混响，那么需要一个很长的X（n）作为输入才能估计回声信号的函数。  这会导致滤波器算力增加，难以实现实时性。

解决方案：

可以通过估计延迟来减少公式5中的算力需求，即减少计算Wk。

延迟估计的方法也比较简单，其实就是移动远端信号的起始位置，然后和回声信号计算互相关性，并找到互相关最大的位置。这个位置就是我们要的延迟。

4.2 双讲检测

双讲：

远端和近端都存在音频信号。

问题场景：

当双讲场景时， 由于NLMS是由于对回声信号进行估计的，若此时还用麦克风采集的信号作为回声信号，会导致滤波器无法收敛到正确位置，产生回声泄漏或近端语音受损。

解决方案：

先判断是单讲还是双讲；

检测方法是结合能量和远、近信号的相干性做一个判断。比如远端和近端能量都比较高但相干性不强，说明加入了近端声音，也就是双讲状态。

滤波器更新策略：

若为单讲，滤波器系数照常跌代更新；

若为双讲，调节步长因子或减缓滤波器的更新。

例子：

如果和对方打网络电话的时候，我们从一个房间走到另一个房间，比如从会议室走到走廊，对面反馈说听到了回声。这其实就和 AEC 的双讲时的策略有关，如果你和对端同时说话恰巧在此刻你换了个地方，也就是回声路径发生了改变。          但由于是双讲的状态，滤波器没有及时更新，这时候就会漏回声。所以双讲检测可以防止滤波器发散。       但这其实也并不是一个完美的解决方案，可能还会导致回声泄漏。只是这种双讲时，恰巧换房间的情况不是那么常见，所以双讲检测依然是回声策略中常见的调整依据。

4.3 非线性

问题场景：

LMS/NLMS算法实际上是估计一个线性的滤波器，无法模拟扬声器、麦克风可能导致的非线性的变换。   比如一些廉价的或声学特性较差的设备 导致的非线性失真较多，所以出现回声概率较大。

解决方案：

一般在线性回声处理后再集联一个非线性处理，来处理线性处理后的残留噪声。   同时非线性处理需要兼顾不同设备与环境，是一个很有挑战的事情。

另外出现不少基于机器学习的解决非线性的方案见下一讲。

五. 小结

由于采集和播放设备的耦合，在实时音频互动领域，回声消除是实时音频链路中重要的一环。常见回声消除流程：

1. 双讲检测
2. 延迟估计
3. 线性回声消除
4. 非线性回声消除

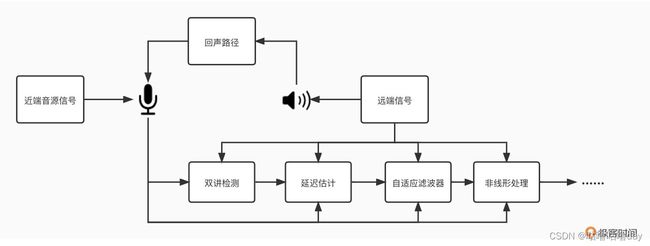
流程图如下：

另外一般把回声消除模块放在音频采集模块后，再做降噪、增益等，也是为了避免音频处理对回声路径的复杂性的增加。

回声消除算法在已知一个音源信号的条件下，在多音源混合的音频中消除这一音源。        所以有的时候回声消除也被用来做一些音源分离的事情。比如一首歌你已经有伴奏的情况下，对人声和伴奏混合在一起的歌曲，用回声消除就可以提取到清唱（也就是没有伴奏的纯人声）。

思考题：

有的时候设备或者 App 在使用过程中还是会频繁地出现回声泄漏，但是带上耳机似乎大部分回声问题就可以解决，这背后的原理是什么呢？

答：带上耳机后， 扬声器不再发声。因而远端声音无法进入到麦克，采集的信号就不会存在远端的声音信息，因而没有回声。