Vision Transformer

Vision Transformer

1. 模型介绍

在计算机视觉领域中，多数算法都是保持CNN整体结构不变，在CNN中增加attention模块或者使用attention模块替换CNN中的某些部分。有研究者提出，没有必要总是依赖于CNN。因此，作者提出ViT算法，仅仅使用Transformer结构也能够在图像分类任务中表现很好。

受到NLP领域中Transformer成功应用的启发，ViT算法中尝试将标准的Transformer结构直接应用于图像，并对整个图像分类流程进行最少的修改。具体来讲，ViT算法中，会将整幅图像拆分成小图像块，然后把这些小图像块的线性嵌入序列作为Transformer的输入送入网络，然后使用监督学习的方式进行图像分类的训练。

该算法在中等规模（例如ImageNet）以及大规模（例如ImageNet-21K、JFT-300M）数据集上进行了实验验证，发现：

• Transformer相较于CNN结构，缺少一定的平移不变性和局部感知性，因此在数据量不充分时，很难达到同等的效果。具体表现为使用中等规模的ImageNet训练的Transformer会比ResNet在精度上低几个百分点。
• 当有大量的训练样本时，结果则会发生改变。使用大规模数据集进行预训练后，再使用迁移学习的方式应用到其他数据集上，可以达到或超越当前的SOTA水平。

2. 模型结构与实现

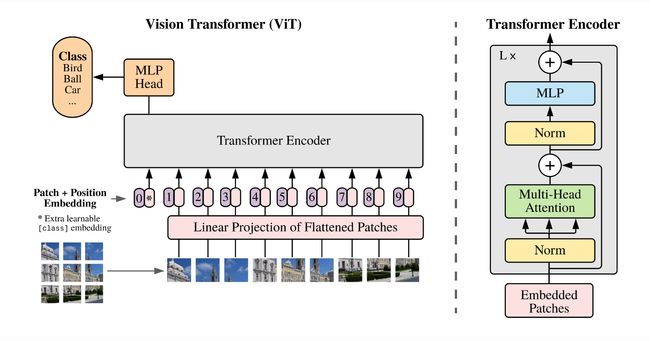
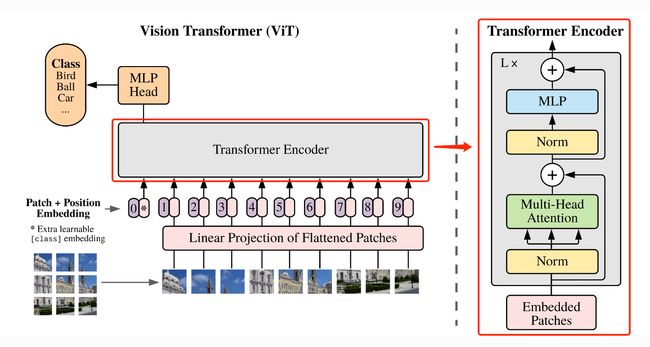
ViT算法的整体结构如 图1 所示。

图1 ViT算法结构示意图

2.1. 图像分块嵌入

考虑到在Transformer结构中，输入是一个二维的矩阵，矩阵的形状可以表示为 $(N,D)$，其中 $N$ 是sequence的长度，而 $D$ 是sequence中每个向量的维度。因此，在ViT算法中，首先需要设法将 $H\times W\times C$ 的三维图像转化为 $(N,D)$ 的二维输入。

ViT中的具体实现方式为：将 $H\times W\times C$ 的图像，变为一个 $N\times (P^2\times C)$ 的序列。这个序列可以看作是一系列展平的图像块，也就是将图像切分成小块后，再将其展平。该序列中一共包含了 $N=HW/P^2$ 个图像块，每个图像块的维度则是 $(P^2\times C)$。其中 $P$ 是图像块的大小，$C$ 是通道数量。经过如上变换，就可以将 $N$ 视为sequence的长度了。

但是，此时每个图像块的维度是 $(P^2\times C)$，而我们实际需要的向量维度是 $D$，因此我们还需要对图像块进行 Embedding。这里 Embedding 的方式非常简单，只需要对每个 $(P^2\times C)$ 的图像块做一个线性变换，将维度压缩为 $D$ 即可。

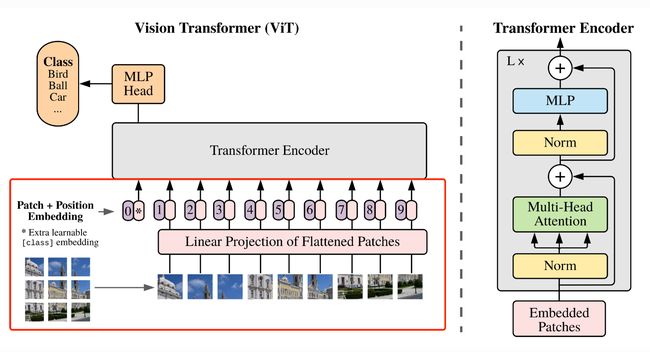
上述对图像进行分块以及 Embedding 的具体方式如 图2 所示。

图2 图像分块嵌入示意图

具体代码实现如下所示:

class PatchEmbed(nn.Module):
    """
    2D Image to Patch Embedding
    """
    def __init__(self, img_size=224, patch_size=16, in_c=3, embed_dim=768, norm_layer=None):
        super().__init__()
        img_size = (img_size, img_size)
        patch_size = (patch_size, patch_size)
        self.img_size = img_size
        self.patch_size = patch_size
        self.grid_size = (img_size[0] // patch_size[0], img_size[1] // patch_size[1])
        self.num_patches = self.grid_size[0] * self.grid_size[1]

        self.proj = nn.Conv2d(in_c, embed_dim, kernel_size=patch_size, stride=patch_size)
        self.norm = norm_layer(embed_dim) if norm_layer else nn.Identity()

    def forward(self, x):
        B, C, H, W = x.shape
        assert H == self.img_size[0] and W == self.img_size[1], \
            f"Input image size ({H}*{W}) doesn't match model ({self.img_size[0]}*{self.img_size[1]})."

        # flatten: [B, C, H, W] -> [B, C, HW]
        # transpose: [B, C, HW] -> [B, HW, C]
        x = self.proj(x).flatten(2).transpose(1, 2)
        x = self.norm(x)
        return x

2.2. 多头注意力

将图像转化为 $N\times (P^2\times C)$ 的序列后，就可以将其输入到 Transformer 结构中进行特征提取了，如 图3 所示。

图3 多头注意力示意图

Transformer 结构中最重要的结构就是 Multi-head Attention，即多头注意力结构。具有2个head的 Multi-head Attention 结构如 图4 所示。输入 $a^i$ 经过转移矩阵，并切分生成 $q^{(i,1)}$、$q^{(i,2)}$、$k^{(i,1)}$、$k^{(i,2)}$、$v^{(i,1)}$、$v^{(i,2)}$，然后 $q^{(i,1)}$ 与 $k^{(i,1)}$ 做 attention，得到权重向量 $\alpha$，将 $\alpha$ 与 $v^{(i,1)}$ 进行加权求和，得到最终的 $b^{(i,1)}(i=1,2,\dots ,N)$，同理可以得到 $b^{(i,2)}(i=1,2,\dots ,N)$。接着将它们拼接起来，通过一个线性层进行处理，得到最终的结果。

图4 多头注意力

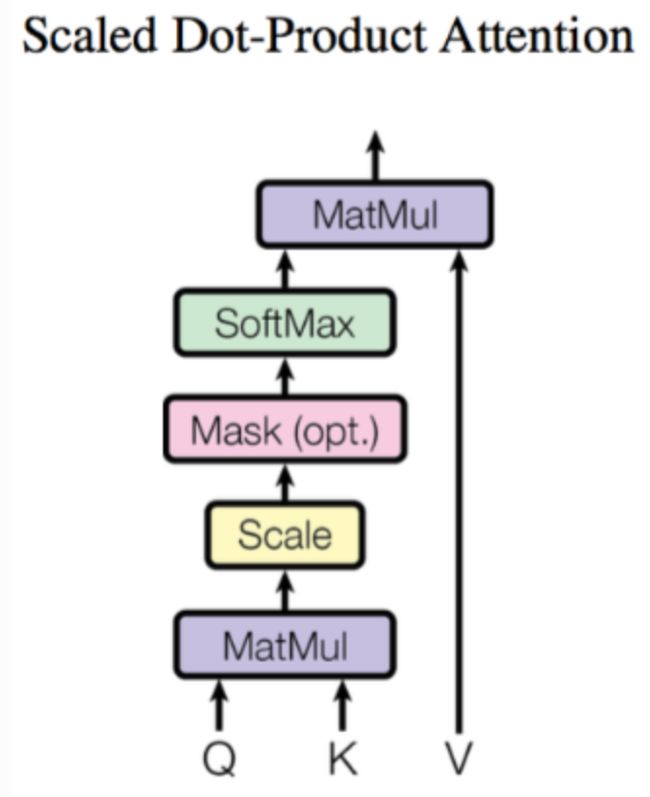
其中，使用 $q^{(i,j)}$、$k^{(i,j)}$ 与 $v^{(i,j)}$ 计算 $b^{(i,j)}(i=1,2,\dots ,N)$ 的方法是缩放点积注意力 (Scaled Dot-Product Attention)。 结构如 图5 所示。首先使用每个 $q^{(i,j)}$ 去与 $k^{(i,j)}$ 做 attention，这里说的 attention 就是匹配这两个向量有多接近，具体的方式就是计算向量的加权内积，得到 ${\alpha }_{(i,j)}$。这里的加权内积计算方式如下所示：

$${\alpha }_{(1,i)}=q^1\ast k^i/\sqrt{d}$$

其中，$d$ 是 $q$ 和 $k$ 的维度，因为 $q\ast k$ 的数值会随着维度的增大而增大，因此除以 $\sqrt{d}$ 的值也就相当于归一化的效果。

接下来，把计算得到的 ${\alpha }_{(i,j)}$ 取 softmax 操作，再将其与 $v^{(i,j)}$ 相乘。

图5 缩放点积注意力

具体代码实现如下所示:

class Attention(nn.Module):
    def __init__(self,
                 dim,   # 输入token的dim
                 num_heads=8,
                 qkv_bias=False,
                 qk_scale=None,
                 attn_drop_ratio=0.,
                 proj_drop_ratio=0.):
        super(Attention, self).__init__()
        self.num_heads = num_heads
        head_dim = dim // num_heads
        self.scale = qk_scale or head_dim ** -0.5
        self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop_ratio)
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop_ratio)

    def forward(self, x):
        # [batch_size, num_patches + 1, total_embed_dim]
        B, N, C = x.shape

        # qkv(): -> [batch_size, num_patches + 1, 3 * total_embed_dim]
        # reshape: -> [batch_size, num_patches + 1, 3, num_heads, embed_dim_per_head]
        # permute: -> [3, batch_size, num_heads, num_patches + 1, embed_dim_per_head]
        qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
        # [batch_size, num_heads, num_patches + 1, embed_dim_per_head]
        q, k, v = qkv[0], qkv[1], qkv[2]  # make torchscript happy (cannot use tensor as tuple)

        # transpose: -> [batch_size, num_heads, embed_dim_per_head, num_patches + 1]
        # @: multiply -> [batch_size, num_heads, num_patches + 1, num_patches + 1]
        attn = (q @ k.transpose(-2, -1)) * self.scale
        attn = attn.softmax(dim=-1)
        attn = self.attn_drop(attn)

        # @: multiply -> [batch_size, num_heads, num_patches + 1, embed_dim_per_head]
        # transpose: -> [batch_size, num_patches + 1, num_heads, embed_dim_per_head]
        # reshape: -> [batch_size, num_patches + 1, total_embed_dim]
        x = (attn @ v).transpose(1, 2).reshape(B, N, C)
        x = self.proj(x)
        x = self.proj_drop(x)
        return x

2.3. 多层感知机（MLP）

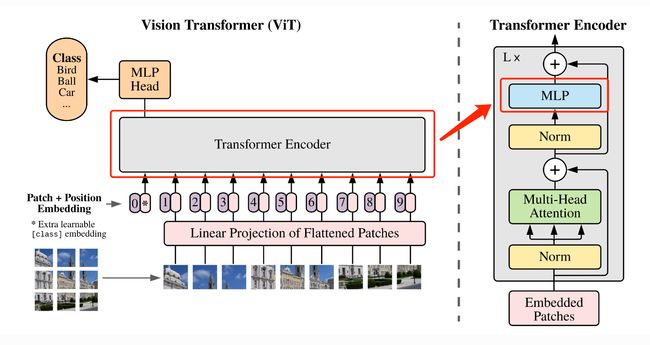
Transformer 结构中还有一个重要的结构就是 MLP，即多层感知机，如 图6 所示。

具体代码实现如下所示:

class Mlp(nn.Module):
    """
    MLP as used in Vision Transformer, MLP-Mixer and related networks
    """
    def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
        super().__init__()
        out_features = out_features or in_features
        hidden_features = hidden_features or in_features
        self.fc1 = nn.Linear(in_features, hidden_features)
        self.act = act_layer()
        self.fc2 = nn.Linear(hidden_features, out_features)
        self.drop = nn.Dropout(drop)

    def forward(self, x):
        x = self.fc1(x)
        x = self.act(x)
        x = self.drop(x)
        x = self.fc2(x)
        x = self.drop(x)
        return x

2.4. DropPath

除了以上重要模块意外，代码实现过程中还使用了DropPath（Stochastic Depth）来代替传统的Dropout结构，DropPath可以理解为一种特殊的 Dropout。其作用为：若x为输入的张量，其通道为[B,C,H,W]，那么drop_path的含义为在一个Batch_size中，随机有drop_prob的样本，不经过主干，而直接由分支进行恒等映射。

具体实现如下：

def drop_path(x, drop_prob: float = 0., training: bool = False):
    if drop_prob == 0. or not training:
        return x
    keep_prob = 1 - drop_prob
    shape = (x.shape[0],) + (1,) * (x.ndim - 1)  # work with diff dim tensors, not just 2D ConvNets
    random_tensor = keep_prob + torch.rand(shape, dtype=x.dtype, device=x.device)
    random_tensor.floor_()  # binarize
    output = x.div(keep_prob) * random_tensor
    return output


class DropPath(nn.Module):
    """
    Drop paths (Stochastic Depth) per sample  (when applied in main path of residual blocks).
    """
    def __init__(self, drop_prob=None):
        super(DropPath, self).__init__()
        self.drop_prob = drop_prob

    def forward(self, x):
        return drop_path(x, self.drop_prob, self.training)

2.5. 基础模块

基于上面实现的 Attention、MLP、DropPath模块就可以组合出 Vision Transformer 模型的一个基础模块，如 图8 所示。

图8 基础模块示意图

基础模块的具体实现如下：

class Block(nn.Module):
    def __init__(self,
                 dim,
                 num_heads,
                 mlp_ratio=4.,
                 qkv_bias=False,
                 qk_scale=None,
                 drop_ratio=0.,
                 attn_drop_ratio=0.,
                 drop_path_ratio=0.,
                 act_layer=nn.GELU,
                 norm_layer=nn.LayerNorm):
        super(Block, self).__init__()
        self.norm1 = norm_layer(dim)
        self.attn = Attention(dim, num_heads=num_heads, qkv_bias=qkv_bias, qk_scale=qk_scale,
                              attn_drop_ratio=attn_drop_ratio, proj_drop_ratio=drop_ratio)
        # NOTE: drop path for stochastic depth, we shall see if this is better than dropout here
        self.drop_path = DropPath(drop_path_ratio) if drop_path_ratio > 0. else nn.Identity()
        self.norm2 = norm_layer(dim)
        mlp_hidden_dim = int(dim * mlp_ratio)
        self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer, drop=drop_ratio)

    def forward(self, x):
        x = x + self.drop_path(self.attn(self.norm1(x)))
        x = x + self.drop_path(self.mlp(self.norm2(x)))
        return x

2.6. 定义ViT网络

基础模块构建好后，就可以构建完整的ViT网络了。在构建完整网络结构之前，还需要给大家介绍几个模块：

• Class Token

假设我们将原始图像切分成 $3\times 3$ 共9个小图像块，最终的输入序列长度却是10，也就是说我们这里人为的增加了一个向量进行输入，我们通常将人为增加的这个向量称为 Class Token。那么这个 Class Token 有什么作用呢？

我们可以想象，如果没有这个向量，也就是将 $N=9$ 个向量输入 Transformer 结构中进行编码，我们最终会得到9个编码向量，可对于图像分类任务而言，我们应该选择哪个输出向量进行后续分类呢？因此，ViT算法提出了一个可学习的嵌入向量 Class Token，将它与9个向量一起输入到 Transformer 结构中，输出10个编码向量，然后用这个 Class Token 进行分类预测即可。

其实这里也可以理解为：ViT 其实只用到了 Transformer 中的 Encoder，而并没有用到 Decoder，而 Class Token 的作用就是寻找其他9个输入向量对应的类别。

• Positional Encoding

按照 Transformer 结构中的位置编码习惯，这个工作也使用了位置编码。不同的是，ViT 中的位置编码没有采用原版 Transformer 中的 $sincos$ 编码，而是直接设置为可学习的 Positional Encoding。

• MLP Head

得到输出后，ViT中使用了 MLP Head对输出进行分类处理，这里的 MLP Head 由 LayerNorm 和两层全连接层组成，并且采用了 GELU 激活函数。

具体代码如下所示：

class VisionTransformer(nn.Module):
    def __init__(self, img_size=224, patch_size=16, in_c=3, num_classes=1000,
                 embed_dim=768, depth=12, num_heads=12, mlp_ratio=4.0, qkv_bias=True,
                 qk_scale=None, drop_ratio=0.,
                 attn_drop_ratio=0., drop_path_ratio=0., embed_layer=PatchEmbed, norm_layer=None,
                 act_layer=None):
        """
        Args:
            img_size (int, tuple): input image size
            patch_size (int, tuple): patch size
            in_c (int): number of input channels
            num_classes (int): number of classes for classification head
            embed_dim (int): embedding dimension
            depth (int): depth of transformer
            num_heads (int): number of attention heads
            mlp_ratio (int): ratio of mlp hidden dim to embedding dim
            qkv_bias (bool): enable bias for qkv if True
            qk_scale (float): override default qk scale of head_dim ** -0.5 if set
            drop_ratio (float): dropout rate
            attn_drop_ratio (float): attention dropout rate
            drop_path_ratio (float): stochastic depth rate
            embed_layer (nn.Module): patch embedding layer
            norm_layer: (nn.Module): normalization layer
        """
        super(VisionTransformer, self).__init__()
        self.num_classes = num_classes
        self.num_features = self.embed_dim = embed_dim  # num_features for consistency with other models
        self.num_tokens = 2 if distilled else 1
        norm_layer = norm_layer or partial(nn.LayerNorm, eps=1e-6)
        act_layer = act_layer or nn.GELU

        self.patch_embed = embed_layer(img_size=img_size, patch_size=patch_size, in_c=in_c, embed_dim=embed_dim)
        num_patches = self.patch_embed.num_patches

        self.cls_token = nn.Parameter(torch.zeros(1, 1, embed_dim))
        self.pos_drop = nn.Dropout(p=drop_ratio)

        dpr = [x.item() for x in torch.linspace(0, drop_path_ratio, depth)]  # stochastic depth decay rule
        self.blocks = nn.Sequential(*[
            Block(dim=embed_dim, num_heads=num_heads, mlp_ratio=mlp_ratio, qkv_bias=qkv_bias, qk_scale=qk_scale,
                  drop_ratio=drop_ratio, attn_drop_ratio=attn_drop_ratio, drop_path_ratio=dpr[i],
                  norm_layer=norm_layer, act_layer=act_layer)
            for i in range(depth)
        ])
        self.norm = norm_layer(embed_dim)

        # Classifier head(s)
        self.head = nn.Linear(self.num_features, num_classes) if num_classes > 0 else nn.Identity()


        # Weight init
        nn.init.trunc_normal_(self.pos_embed, std=0.02)
        if self.dist_token is not None:
            nn.init.trunc_normal_(self.dist_token, std=0.02)

        nn.init.trunc_normal_(self.cls_token, std=0.02)
        self.apply(_init_vit_weights)


    def forward_features(self, x):
        # [B, C, H, W] -> [B, num_patches, embed_dim]
        x = self.patch_embed(x)  # [B, 196, 768]
        # [1, 1, 768] -> [B, 1, 768]
        cls_token = self.cls_token.expand(x.shape[0], -1, -1)

        x = torch.cat((cls_token, x), dim=1)  # [B, 197, 768]


        x = self.pos_drop(x + self.pos_embed)
        x = self.blocks(x)
        x = self.norm(x)
        return x[:, 0]

    def forward(self, x):
        x = self.forward_features(x)
        x = self.head(x)
        return x

def _init_vit_weights(m):
    """
    ViT weight initialization
    :param m: module
    """
    if isinstance(m, nn.Linear):
        nn.init.trunc_normal_(m.weight, std=.01)
        if m.bias is not None:
            nn.init.zeros_(m.bias)
    elif isinstance(m, nn.Conv2d):
        nn.init.kaiming_normal_(m.weight, mode="fan_out")
        if m.bias is not None:
            nn.init.zeros_(m.bias)
    elif isinstance(m, nn.LayerNorm):
        nn.init.zeros_(m.bias)
        nn.init.ones_(m.weight)

3. 模型特点

• 作为CV领域最经典的 Transformer 算法之一，不同于传统的CNN算法，ViT尝试将标准的Transformer结构直接应用于图像，并对整个图像分类流程进行最少的修改。
• 为了满足 Transformer 输入结构的要求，将整幅图像拆分成小图像块，然后把这些小图像块的线性嵌入序列输入到网络。同时，使用了Class Token的方式进行分类预测。