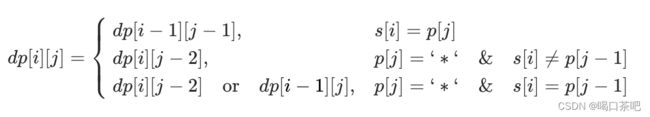LeetCode HOT 100VI
目录
208:实现 Trie (前缀树)(很重要!其实很好理解)
148:排序链表(排序!!)
128:最长连续序列
42:接雨水(重点题)
4:寻找两个正序数组的中位数(重点题)
10:!!正则表达式匹配!!(重中之重!!)
33:搜索旋转排序数组
72:编辑距离
32:最长有效括号
208:实现 Trie (前缀树)(很重要!其实很好理解)
思路:构建字典树,树的节点对应26个小写字母。用当前的字符-‘a’的asc码得到的数字就是索引,0对应的是a,25对应的是z。树中每个节点都有两个字段children和end
- insert功能:判断当前字符对应的索引在树中是否为空,为空则需要插入字符,不为空则代表已经存入。当最后一个字符插入后需要将其标记为结尾字符,即node.end = true。
- search功能:全匹配,首先依次匹配输入字符串里每个字符是否在树中存在,同时满足最后一个字符存在且end标记是true
- startsWith:前缀搜索,与上个功能相比不需要最后结尾标记的判断
(注:这个解法直接开了26叉,方便搜索的时候定位,空间换时间。也可以有几叉开几叉)
class Trie {
public Trie[] children;
public boolean end;
public Trie() {
children = new Trie[26];
//用来判断当前字符是否为字符串的结尾
end = false;
}
public void insert(String word) {
Trie node = this;
for(int i = 0; i < word.length(); i++){
char c = word.charAt(i);
int index = c - 'a'; //减字符a的asc码
if(node.children[index] == null) node.children[index] = new Trie();
node = node.children[index];
}
//标为true代表当前字符为最后一个
node.end = true;
}
public boolean search(String word) {
Trie node = Prefix(word);
//当前字符全部存在且结尾标记为true才算是匹配成功
return node != null && node.end;
}
public boolean startsWith(String prefix) {
//前缀搜索,与search的区别在于不用判断结尾true
return Prefix(prefix) != null;
}
public Trie Prefix(String prefix){
Trie node = this;
for(int i = 0; i < prefix.length(); i++){
char c = prefix.charAt(i);
int index = c - 'a';
if(node.children[index] == null) return null;
node = node.children[index];
}
return node;
}
}
/**
* Your Trie object will be instantiated and called as such:
* Trie obj = new Trie();
* obj.insert(word);
* boolean param_2 = obj.search(word);
* boolean param_3 = obj.startsWith(prefix);
*/148:排序链表(排序!!)
思路:归并排序。
- node.next是指出去node链表当前节点以外所有节点,并不是仅仅指当前节点的下一个节点
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode sortList(ListNode head) {
if(head == null || head.next == null) return head;
ListNode fast = head.next, slow = head;
while(fast != null && fast.next != null){
slow = slow.next;
fast = fast.next.next;
}
ListNode temp = slow.next;
slow.next = null;
ListNode left = sortList(head);
ListNode right = sortList(temp);
ListNode node = new ListNode(0);
ListNode res = node;
while(left != null && right != null){
//进入划分最后一阶段--两两交换
if(left.val < right.val){
node.next = left;
left = left.next;
}else{
node.next = right;
right = right.next;
}
node = node.next;
}
node.next = left != null ? left : right;
return res.next;
}
}128:最长连续序列
思路:遍历数组,首先判断每个元素的num-1是否存在,存在的话还需要从num-1开始匹配,不存在的话再循环判断num+1是否存在,存在多长,做记录。
class Solution {
public int longestConsecutive(int[] nums) {
Set hash = new HashSet();
for(int num : nums){
hash.add(num);
}
int res = 0;
for(int num : hash){
if(!hash.contains(num - 1)){
//当存在num-1的时候就需要从num-1开始匹配,所以需要判断一下避免重复搜索
int cur = num;
int length = 1;
while(hash.contains(cur + 1)){
cur += 1;
length += 1;
}
res = Math.max(res, length);
}
}
return res;
}
} 42:接雨水(重点题)
思路:暴力解法存在重复遍历的问题,利用动态规划可以解决,用数组存放遍历到当前时两侧最高的边。寻找的时候不包括当前列,所以max的时候用的是动态数组上一个结果和当前列左右两侧的边进行比较选出大的。
//---------------- 动态规划 ----------------
class Solution {
public int trap(int[] height) {
int res = 0;
int[] leftMax = new int[height.length];
int[] rightMax = new int[height.length];
//找左右两侧最高边的时候不包括当前的列,所以是i-1和i+1
for(int i = 1; i < height.length - 1; i++){
//正着存放
leftMax[i] = Math.max(leftMax[i - 1], height[i - 1]);
}
for(int i = height.length - 2; i >= 0; i--){
//倒着存放
rightMax[i] = Math.max(rightMax[i + 1], height[i + 1]);
}
for(int i = 1; i < height.length - 1; i++){
int min = Math.min(leftMax[i], rightMax[i]);
if(min > height[i]) res += (min - height[i]);
}
return res;
}
}
//---------------- 暴力解法(不提倡) ----------------
class Solution {
public int trap(int[] height) {
int res = 0;
for(int i = 1; i < height.length - 1; i++){
int leftMax = 0;
for(int j = i - 1; j >= 0; j--){
if(height[j] > leftMax) leftMax = height[j];
}
int rightMax = 0;
for(int j = i + 1; j < height.length; j++){
if(height[j] > rightMax) rightMax = height[j];
}
int min = Math.min(leftMax, rightMax);
if(height[i] < min){
res += (min - height[i]);
}
}
return res;
}
}4:寻找两个正序数组的中位数(重点题)
思路:两个指针分别从两个数组里查找中位数,两个数组都是各自升序排列,所以总长度为奇数的时候第sumLen/2个数为中位数,总长度为偶数时(sumLen/2 - 1 + sumLen/2)/2为中位数,所以只用循环sumLen/2 + 1次
- 当p1长度在nums1长度范围内且其对应元素小于p2对应元素,p1向后移动一位(但在判断p1与p2对应元素大小的时候要判断p2是否还在nums2长度范围内,避免数组越界)
- 反之p2移动
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int sumLen = nums1.length + nums2.length;
int p1 = 0, p2 = 0;
int pre = -1, cur = -1;
for(int i = 0; i <= sumLen / 2; i++){
//长度为偶数需要当前+上一个 / 2计算中位数
pre = cur;
if(p1 < nums1.length && (p2 >= nums2.length || nums1[p1] < nums2[p2]))
//当p1没有超出nums1长度范围且对应的元素小于p2对应的元素,则p1向后移动
//p2 >= nums2.length是为了避免数组越界,可能上一轮循环结束的时候p2已经走到了最后
cur = nums1[p1++];
else
cur = nums2[p2++];
}
//长度是偶数
if((sumLen & 1) == 0) return (cur + pre) / 2.0;
else return cur;
}
}10:!!正则表达式匹配!!(重中之重!!)
思路:动态规划。神题解:力扣
状态方程dp[ i ][ j ]表示s中第 i 个字符和p中第 j 个字符是否相同,相同为true不同为false,dp存放的状态可以由已存在的状态转移过来(即状态转移方程)
- 当p[ j ]是字母a~z:s[ i ]与之匹配的时候,dp[ i ][ j ]的状态可以由dp[ i - 1 ][ j - 1 ]转移得来;不匹配的话为false
- 当p[ j ]是‘ . ’:s[ i ]和p[ j ]一定匹配,所以dp[ i ][ j ]的状态由dp[ i - 1 ][ j - 1 ]转移
- 当p[ j ]是‘ * ’:首先要清楚*的作用不止有补充还有消除和什么都不做,作用于前一个字符。所以遇到*的时候需要和s[ i ]及前面相同的字符循环匹配。s中有多少k个相同的字符,那么dp[ i ][ j ]的状态就可以由dp[ i - k ][ j - 2 ]转移得来,也就是s中重复字符的前一个字符和p中*的前前个字符的状态,而这个状态方程的需要满足*前一个字符可以与s中重复字符匹配成功,即满足s[ i ] = s[ i - 1] = ... = s[ i - k + 1] = p[ j - 1]。接下来就是推导状态方程了:
综上所诉可以得到总的状态转移方程:
p为空时候除了s也为空,其他所有情况都不匹配,所以除了dp[0][0]第0列均为false;
s为空的时候,如果p中有*可以消除,但*只能消除它前一个字符。
初始化这块还需要再理解理解。
class Solution {
public boolean isMatch(String s, String p) {
int m = s.length(), n = p.length();
boolean[][] dp = new boolean[m + 1][n + 1];
dp[0][0] = true;
for(int j = 1; j <= n; j++){
//dp的第一行和第一列分别存放s和p为空的情况
//不初始化的话会导致下一个循环用第0行或第0列的状态可能出错
if(p.charAt(j - 1) == '*') dp[0][j] = dp[0][j - 2];
}
for(int i = 1; i <= m; i++){
//j不能从i开始,否则只有一个.的时候判断会出错
for(int j = 1; j <= n; j++){
if(s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.'){
dp[i][j] = dp[i - 1][j - 1];
}else if(p.charAt(j - 1) == '*'){
if(s.charAt(i - 1) != p.charAt(j - 2) && p.charAt(j - 2) != '.'){
dp[i][j] = dp[i][j - 2];
}else{
dp[i][j] = dp[i][j - 2] | dp[i - 1][j];
}
}
}
}
return dp[m][n];
}
}33:搜索旋转排序数组
思路:二分查找。当中间指针大于第0个元素,那么前半部分肯定是有序递增的,后半部分不一定;小于的话前半部分有转折点,后半部分肯定是有序的。
要注意的是当nums[mid] = nums[0] != target时说明mid=0,因为nums里无重复数,只能向后查找,放到nums[mid] < nums[0]里的话kennel会导致right越界为-1
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
if(nums.length == 0) return -1;
else if(nums.length == 1) return nums[0] == target ? 0 : -1;
while(left <= right){
int mid = (left + right) / 2;
if(nums[mid] == target) return mid;
if(nums[mid] >= nums[0]){
//前半部分肯定是递增的
if(nums[0] <= target && target < nums[mid]) right = mid - 1;
else left = mid + 1;
}else{
//后半部分肯定是递增的
if(nums[mid] < target && target <= nums[nums.length - 1])
left = mid + 1;
else right = mid - 1;
}
}
return -1;
}
}72:编辑距离
思路:动态规划,参考题解:力扣
dp[ i ][ j ]代表的是word1的前 i 个要变成word2前 j 个最少需要几步,所以可以得到状态转移方程:
- 增:dp[ i ][ j ] = dp[ i ][ j - 1 ] + 1(相当于word2进行删除操作)
- 删:dp[ i ][ j ] = dp[ i - 1 ][ j ] + 1
- 改:dp[ i ][ j ] = dp[ i - 1 ][ j - 1 ] + 1
当两个字符相同的时候直接由dp[ i - 1 ][ j - 1 ]转移得来,不用+1
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length(), len2 = word2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
//第一行是word1为空的时候,变成word2前i个最少需要i步
for(int i = 1; i <= len1; i++) dp[i][0] = i;
//同上
for(int j = 1; j <= len2; j++) dp[0][j] = j;
for(int i = 1; i <= len1; i++){
for(int j = 1; j <= len2; j++){
dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
if(word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[i][j] = Math.min(dp[i][j], dp[i - 1][j - 1]);
}
}
}
return dp[len1][len2];
}
}32:最长有效括号
思路:有效括号长度 = ' ) '的下标 - ' ( '的下标 + 1,即' ) '的下标 - ' ( '的前一个的下标。当出现' ( '的时候记录它的索引;当出现' ) '的时候首先判断是否有它匹配的' ( ',即判断stack是否为空。
- 为空的话说明没有其匹配的' ( ',所以记录' ) '的下标,用于后面有匹配的括号计算长度
- 不为空的话计算当前有效括号的长度
⚠️:栈顶元素应该是最后一个没被匹配的' ) '的下标,如果第一个就是' ( ',会将它的索引放进去,不满足第一句话,所以初始化的时候将第一个设置为-1。
class Solution {
public int longestValidParentheses(String s) {
Deque stack = new LinkedList();
int res = 0;
stack.push(-1);
for(int i = 0; i < s.length(); i++){
if(s.charAt(i) == '(') stack.push(i);
else{
stack.pop();
if(stack.isEmpty()) stack.push(i);
else res = Math.max(res, i - stack.peek());
}
}
return res;
}