使用条件分布模态流进行多变量概率时序预测
使用条件分布模态流进行多变量概率时序预测
译者的话
时序预测是一个古老的话题。有许多基于数理统计的经典算法曾经大放异彩。但随着大数据时代的到来,数据量的急剧增长以使得传统的分析方式在可行性上已初现窘迫,在预测精度及预测步长上也难以满足当代社会的需求,在时序数据表征的随机性太强的情形下,各种假设更是失去了效力。因此这种end-to-end的深度学习时序预测方法应运而生,2018年至今短短数年,便是红火如斯。
从ARIMA、faceBook的Prophet、再到LSTM、DeepAR多个技术选型的更改皆是因为预测准确性到达瓶颈后的为求突破的艰难抉择。因此对DeepAR的易用性和预测准确性及模型通用性印象深刻。因此更是对Kashif Rasul等人提出的方案充满期待。
笔者翻译此文的主要原因是Kashif Rasul等人提出的本套方案在大多数实际生产环境中训练效率较DeepAR更高,预测范围更紧凑,笔者希望国内同仁也能更早的使用这套方法,到时候互相学习,一起改进岂不是妙哉。
关于Normalizing Flows的中文译名,现在大多数的文献及网络文章中译为‘标准化流’,但译者在本文中,统一将Normalizing Flows翻译为‘分布模态流’,而Conditioned Normalizing Flows译为‘条件分布模态流’,译名可能不甚准确,若各位同仁有其他的想法,欢迎沟通交流。
由于笔者水平有限,译文中难免会有疏漏,若有同仁发现了不妥之处,还望及时指出,原文地址为:Multi-variate Probabilistic Time Series Forecasting via Conditioned Normalizing Flows。另外文中包含许多的深度学习方面的术语,笔者并未在文中给出解释,请诸位自行查阅相关资料。
概要
时间序列预测通常是科学和工程问题,可以辅助决策。在大数据量情形下,假设具有相关性的时序是相互独立的,是进行大规模时序预测的一个简单解决办法。但是,考虑相关性的统计学方法不仅可以提高准确度,还可以进行交互式分析,因此上面这种简单的解决方式似乎不够完美。深度学习方法非常适合此问题,但是多变量模型通常只将分布假设为一些基础的分布并且无法扩展到高维。因此,我们建立了一种动态的多变量时序模型,一种用条件分布模态流代替诸如正态分布、T分布、F分布的数据分布的自回归深度神经网络模型。这种结合使得RNN获得了AR(自回归)的诸多优点,比如在具备高维分布模型、获得更好的预测效果同时,具有流的灵活性和高效的计算效率。我们已经证实,这种算法模型在数千个真实的时间序列上的表现(基于目前标准的评价方式)是目前最先进的。
1.引言
经典的时序预测方法,比如Hyndman & Athanasopoulos (2018)给出的单变量预测方法,需要手动调整季节性等其他的参数。基于RNN的时序预测模型,比如LSTM,变得越来越流行,因为这是一种end-to-end的训练方式,不需要进行复杂特征处理,这也是是深度学习的特点。输出的预测结果既可以是一组值,也可以是一个范围(根据数据分布给出的置信区间)。时序置信区间预测的主要难点在于下游业务如何确定什么样的置信区间是可信的,例如异常检测或(商业)决策。不使用概率建模,就无法区分低噪音和高噪音的场景,然而这对预测来说很重要。值预测模型,忽视了噪声带来的风险,但是对噪声的处理在一些场景下十分重要,比如商业决策。
最后,在许多情况下,各个时间序列在统计上是相互依赖的,并且模型需要具有处理这种情况的能力,以提高预测的准确性(Tsay,2014)。例如,为了建立零售商品需求模型,不仅要考虑商品自身历史销售数据,还要考虑其他竞品市场份额的影响。再比如,用传感器测量交通网中的车流量,一条特定街道的阻塞也会影响附近街道–单变量模型可能无法解释上述影响。
因此我们尝试去设计一种基于概率预测的、end-to-end训练模式的、自回归深度学习时序模型算法,这种模型算法支持多变量时间序列,并且实现分布模态流的动态插拔,就像the Masked Autoregressive Flow (Papamakarios等人,2017) or Real NVP (Dinh 等人,2017)。
这篇论文的主要亮点在于:
-
我们设计了一套针对多变量时间序列的概率方法,这套方法支持受数千个‘因素时间序列’影响的‘目标时间序列’的建模。
-
我们证实,这套模型在小体量的实验集情形下依然能获得不错的效果。
-
这套模型在许多真实数据集上的表现是目前最新进的。
该模型还具有以下优点:
-
基础分布(正态分布、T分布、F分布、贝塔分布等)建模采用条件分布模态流,这种方式支持多种基础分布。
-
由于采用了注意力机制的并行计算因此训练效率很高,不像典型的基于RNN的时序模型。根据经验,我们观察到基于Transformer的模型的训练时间缩短了一个数量级。
整个论文大体结构如下:第2章介绍了一些背景,第3章介绍了本文中涉及相关技术,第4章介绍了我们的算法,第5章展示了我们实验的详细细节,第6章给出了结论。
2.背景
我们简要介绍时间序列预测的现状,并在本节中介绍了我们方法的基本组成部分。
2.1. 时序预测
经典的时序预测方法基本都是基于ARMA和它的变体比如ARIMA。这些方法与特征工程密不可分,他们还遭受维度的诅咒,需要频繁的重新训练,并且专注于模型的可解释性,而不是测试集的准确性。
过去几年中,深度学习模型在许多领域都比传统方法有更好的表现,比如图像处理、语音识别、自然语言处理,当然也包括时序预测,这与NLP中的序列建模相似。现代单变量值预测方法,例如Oreshkin(2020)等,在许多目标领域具有解释力,并且可以进行快速训练。
在控制理论中对经典方法的区间估计已经进行了数十年,例如 Dietz 等人
(1997)。大多数经典的预测文献都集中于值预测,例如未来某个时间点的分布平均值或中位数。在深度学习中,这两种方法要么是对数据分布进行显式建模,要么是如Zhu&Laptev(2018)所述使用贝叶斯神经网络。为了估计潜在的分布,我们可以学习某些目标分布的参数,比如DeepAR(Salinas等,2019b),或者使用混合密度网络(MDN)(Bishop,2006年),例如在用于模拟笔迹的MD-RNN方法(Graves,2013年)。最近,Rangapuram等人(2018)将每个单独时间序列的线性状态空间模型与深度概率模型结合在一起,以获得解释性的时间序列预测。
为了进行完整时序建模,即将‘因素时间序列’考虑进来,可以使用多元高斯过程来获取数据的本源结构(Vandenberg-Rodes&Shahbaba,2015)或者通过RNN习得低阶高斯Copula过程(Salinas等,2019a)。时态正则化矩阵分解框架(Yu等人,2016)建议学习数据依赖关系,从而通过矩阵分解方法预测未来值。LSTNet(Lai等人,2018)使用卷积神经网络(CNN)和RNN构建blocks为值预测的多元时间序列建模。还提出了使用分层的先验贝叶斯模型,以在各个时间序列之间共享statistical strength,同时保持推理的可行性(Chapados,2014年)。Li等人(2019)最近也探索了将多点注意力机制用于时间序列预测,这种方式可以保存更长的历史信息以解决RNN系列(比如LSTM)面临的记忆不够长的问题。
2.2. 通过分布模态流进行概率密度估计
分布模态流(Tabak和Turner,2013)是从 R D R^{D} RD到 R D R^{D} RD的映射,从而将输入空间上的概率密度 p X p\mathcal X pX变换为空间 Z = R D \mathcal Z=R^{D} Z=RD上的一些简单分布(例如,各向同性的高斯分布)。该映射 f : X ↦ Z f:\mathcal X\mapsto \mathcal Z f:X↦Z由一系列双射或可逆函数构成。因此这个转换公式可表述为:
p X ( x ) = p Z ( z ) ∣ d e t ( ∂ f ( x ) ∂ x ) ∣ p\mathcal X(x)=p\mathcal Z(z)\biggl|det(\frac {\partial f(x)} {\partial x})\biggl| pX(x)=pZ(z)∣∣∣∣det(∂x∂f(x))∣∣∣∣
其中 ∂ f ( x ) ∂ x \frac {\partial f(x)} {\partial x} ∂x∂f(x)是函数 f f f在 x x x处的雅可比矩阵。分布模态流的特点是逆函数 x = f − 1 ( z ) x=f^{-1}(z) x=f−1(z)容易求出并且在计算雅可比行列式的时候时间复杂度为O(D)。
Real NVP(Dinh等人,2017)引入的双射-耦合层满足上述两个特性。它保留部分输入不变,另一部分通过一系列变量恒定函数(上标表示坐标索引)
{ y 1 : d = x 1 : d y d + 1 : D = x d + 1 : D ∙ e x p ( s ( x 1 : d ) ) + t ( x 1 : d ) , \begin{cases} y^{1:d}=x^{1:d} \\ y^{d+1:D}=x^{d+1:D} \bullet exp(s(x^{1:d}))+t(x^{1:d}), \end{cases} {y1:d=x1:dyd+1:D=xd+1:D∙exp(s(x1:d))+t(x1:d),
其中 ∙ \bullet ∙是元素级别乘积, s ( ) s() s()为缩放函数, t ( ) t() t()为转换函数,这种算法是由神经网络实现的。非线性的概率密度函数模型 f ( x ) f(x) f(x)是由一系列耦合层通过这种流的形式组成的,这种流将同时改变保留的部分和转换的部分的纬度。通过上述变量的转化方式,可以将流中给定数据点的概率密度函数(PDF)写为:
l o g p X ( x ) = l o g p Z ( z ) + l o g ∣ d e t ( ∂ z / ∂ x ) = l o g p Z ( z ) + ∑ i = 1 K l o g ∣ d e t ( ∂ y i / ∂ y i − 1 ) ∣ ( 1 ) \begin{aligned} logp\mathcal X(x)=logp\mathcal Z(z)+log|det (\partial z /\partial x)\\ =logp\mathcal Z(z)+\sum_{i=1}^K log|det(\partial y_i/\partial y_{i-1})| \\ (1) \end{aligned} logpX(x)=logpZ(z)+log∣det(∂z/∂x)=logpZ(z)+i=1∑Klog∣det(∂yi/∂yi−1)∣(1)
由于the Real NVP的雅可比矩阵是一个分块的三角矩阵(三角矩阵的行列式是对角线元素的乘积),因此可得出下式:
l o g ∣ d e t ( ∂ y i / ∂ y i − 1 ) ∣ = s u m ( l o g ∣ d i a g ( e x p ( s ( y i − 1 ) ) ) ∣ ) ( 2 ) \begin{aligned} log|det(\partial y_i/\partial y_{i-1})|=sum(log|diag(exp(s(y_{i-1})))|)\\ (2) \end{aligned} log∣det(∂yi/∂yi−1)∣=sum(log∣diag(exp(s(yi−1)))∣)(2)
缩放和转换神经网络的权重参数 θ \theta θ的求解方式是取每个批次训练数据D极大似然估计的解的均值,优化器采用梯度下降,公式如下:
L = 1 ∣ D ∣ ∑ x ∈ D l o g p X ( x ; θ ) \mathcal L= \frac 1{ |\mathcal D|} \sum_{x\in \mathcal D}logp\mathcal X(x;\theta) L=∣D∣1x∈D∑logpX(x;θ)
在实践中,批归一化(Ioffe和Szegedy,2015)作为双射用来处理所有连续耦合层的输出,使得分布模态流的训练更平稳。双射使用所有层的均值和标准偏差的加权移动平均值来执行此归一化过程,这个双射必须是可训练或可模拟的。
可以对Real NVP方法进行一般化,从而产生Masked Autoregressive Flows(Papamakarios等人,2017)(MAF),其中将转换层构建为自回归神经网络,这也就意味着,输入 x ∈ R x\in R x∈R和输出 y = ( y 1 , y 2 . . . , y D ) y=(y^1,y^2...,y^D) y=(y1,y2...,yD),需要转换层的变换是可逆的,并且任何输出 y i y^i yi都不要求输入的维度索引≥i(即)(笔者:就是说不能在训练的时候将预测结果给出)。由于该变换的雅可比行列式是三角的,因此这个雅可比行列式是易于求解的。除了使RNN在 x x x的 D D D维上共享参数外,还可以通过使用掩码来避免这种有序计算,并为其指定名称。然而,生成样本所需的逆是有序的。(笔者:当计算是强顺序时,是无法进行并行计算的,从而使得算法耗时增加)
既然缩放和变换函数的逼近函数不需要可逆,那么直接计算条件概率密度函数PDF p X ( x ∣ h ) p\mathcal X(x|h) pX(x∣h)其中 h ∈ R H h \in R^H h∈RH:我们将串起来的缩放函数和转换函数作为耦合层的一个近似,比如将 s ( c o n c a t ( x 1 : d , h ) ) s(concat(x^{1:d},h)) s(concat(x1:d,h))和 t ( c o n c a t ( x 1 : d , h ) ) t(concat(x^{1:d},h)) t(concat(x1:d,h))变为映射 R d + H ↦ R D − d R^{d+H}\mapsto R^{D-d} Rd+H↦RD−d。另外一种近似求解方式是Korshunova等人(2018)提出的在每层中的 s ( ) s() s()和 t ( ) t() t()中增加一个与h相关的偏置项,这种方式不会改变耦合层的对数行列式的值。对我们来讲更重要的是,针对有序数据,使用流行的自回归RNN系列能让不同的学习器共享同一组参数。
对于离散数据,分布具有负无穷大的微分熵,这在训练归一化流量模型时甚至在测试数据上也会导致高到怀疑人生的对数似然。为避免这种情况可以反量化数据,通常通过添加Uniform[0,1)噪声方式来实现。连续模型的对数似然的下界是离散模型的对数似然,如Theis等人所述(2016)。
2.3. 自注意力
基于转换层的自注意力在序列建模方面已经取得了巨大的成功。多点自注意力机制可以让神经网络针对时间序列同时具备长短记忆的能力。重点是,这个转换器接收一个序列 X = [ x 1 , x 2 , . . . , x t ] T ∈ R t × D X=[x_1,x_2,...,x_t]^T \in \Bbb R^{t \times D} X=[x1,x2,...,xt]T∈Rt×D,然后多点自注意力转换这个序列为 H H H个不同的查询矩阵 Q h = X W h Q Q_h=XW_h^Q Qh=XWhQ、键矩阵 K h = X W h K K_h=XW_h^K Kh=XWhK、值矩阵 V h = X W h V V_h=XW_h^V Vh=XWhV,权重 X W h Q 、 X W h K 、 X W h V XW_h^Q、XW_h^K、XW_h^V XWhQ、XWhK、XWhV都是可学习的参数。在这些线性变换之后,the scaled dot-product attention计算一系列矢量输出,计算方式如下:
O h = A t t e n t i o n ( Q h , K h , V h ) = s o f t m a x ( Q h K h T ⋅ M d K ) V h O_h=Attention(Q_h,K_h,V_h)\\=softmax(\frac {Q_hK_h^T \cdot M} {\sqrt {d_K}})V_h Oh=Attention(Qh,Kh,Vh)=softmax(dKQhKhT⋅M)Vh
其中应用掩码M通过将其上三角元素设置为 − ∞ - \infty −∞来滤出right-ward attention(或者叫future information leakage),并用 d K d_K dK(与 W h K W_h^K WhK有相同维度的矩阵)归一化。之后,所有的 H O h H \space O_h H Oh输出被连接起来并再次线性投影。
人们通常在encoder-decoder中使用这种变换,其中编码器用于对时间序列预热,解码器用于学习和自回归生成输出。
3.相关成果
这些模型与这项工作相关的是以某种方式将分布模态流与序列建模结合起来。Transformation Autoregressive Networks(Oliva等人,2018)(TAN),将多元变量 x ∈ R x \in R x∈R的概率密度建模为D个条件分布 ∏ i = 1 D p X ( x i ∣ x i − 1 , x i − 2 , . . . , x 1 ) \prod_{i=1}^D p \mathcal X(x_i|x_{i-1},x_{i-2},...,x_1) ∏i=1DpX(xi∣xi−1,xi−2,...,x1),其中条件来自混合模型中的RNN的状态,然后通过双射进行转换。Pixel SNAIL(Chen等人,2018)方法将核心节点作为条件分布的产物进行建模(可选地,通过一些全局条件进行建模),并通过因果卷积和自注意力(Vaswani等人,2017)方法获取获取长期时间依赖。这些方法对图片等高维数据建模有很好的效果,但对于时间形态的数据才刚开始探索,比如VideoFlow(Kumaret等人,2019),它由分布模态流组成,该分布模态流认为自回归模型每个时间点的隐变量服从高斯分布,高斯分布的参数是流前一时间步的输出。
使用RNN进行多元或时间属性的序列建模不适合并行化。但是,RNN已经显示出在动态序列建模中非常有效,因此我们仍然认为研究具备时间属性的RNN对多变量时间序列预测非常重要。在此方向上的最新工作(Hwang等人,2019)将带有GRU的二分流用于时间属性以研究多元序列数据的条件生成模型。作者使用双向训练程序来学习生成的观测模型,并将其与时态一起通过RNN进行调节,也可以根据(观察到的)协变量进行调节,它们被建模为潜在空间中的附加条件变量,增加分布模态流的维度。另一些相关研究是能够进行高维数据建模的多变量概率时间序列方法。高斯Copula过程方法(Salinas等,2019a)是用高斯copula过程处理输出的基于RNN的时间序列的法,该方法使用低秩协方差结构建模,以减少计算量复杂性并且也可以处理非高斯边际分布。通过使用协方差矩阵的低秩近似解他们获得了一种易于计算的方法,并且能够可以扩展到成千上万的多元维度。接下来我们将把我们的模型与此模型进行比较。
4.时态条件分布模态流
x t i ∈ R f o r i ∈ { 1 , . . . , D } x_t^i \in R \space for \space i \in \{1,...,D\} xti∈R for i∈{1,...,D}表示时间序列,其中t表示时间索引。因此时刻t处的多元向量可表示为 x t ∈ R D x_t \in R^D xt∈RD。时间序列 t ∈ [ 1 , T ] t \in [1,T] t∈[1,T]由完整的时间序列数据采样而来, [ 1 , t 0 ) [1,t_0) [1,t0)为训练数据, [ t 0 , T ] [t_0,T] [t0,T]为测试数据。
在DeepAR(Salinas等人,2019b)模型中,最大化时间序列 x t i x_{t}^i xti在时间步 t t t上的对数似然以得到该时间序列在该窗口的预测值。也就是寻找使对似然最大的分布模型(例如计数数据服从负二项分布)的参数,这是通过从其前一时间步 x i − 1 i x_{i-1}^i xi−1i及其对应的协变量 c t − 1 i c_{t-1}^i ct−1i得出的RNN的状态完成的。分布模型(对于实数数据通常选择高斯模型,对于计数数据通常选择负二项分布模型)应该能最拟合时序数据的统计属性并且存在满足这些分布参数约束条件的(神经网络的)激活函数,比如高斯分布的比例参数可以用softplus()。
多变量实值数据的简单模型可以在emissions中使用因子分解分布。然后,共享参数可以通过时间组件学习各个时间序列的模式,但是没有捕捉到模型的emissions中的依赖关系。为此,必须对每个时间步的完整联合分布进行建模,例如使用多变量高斯模型。然而,全协方差矩阵的建模不仅增加了 O ( D 2 ) O(D^2) O(D2)的神经网络参数个数,增加了学习难度,而且当D较大时,计算网络的损失也变得昂贵。此外,emissions的统计依赖性将仅限于二级效应。Salinas等人将这些模型称为Vec LSTM(2019a年)。
图1.RNN条件下的Real NVP模型在时间t时的示意图,由K个coupling层和batch Norm层组成,在每个coupling层中,我们将 x t x_t xt及RNN转换后的输出作为条件,而RNN输入为上一时间步 x t − 1 x_{t-1} xt−1及其协变量 c t − 1 c_{t-1} ct−1,其中前者是时间相关的特征后者是时间无关的特征。
针对有 D D D相互作用时间序列我们希望建立一个可扩展的模型,并使得该模型可以灵活挑选的分布模型,以便捕捉和表示高阶矩。为此,我们使用流式算法(例如Real NVP)为所有时间序列 p X ( x t ∣ h t ; θ ) p \mathcal X(x_t |h_t;θ) pX(xt∣ht;θ)在时间t建立了条件联合分布模型,该流式算法条件是时间t处RNN的隐藏状态,或是从注意模块嵌入到t的时间序列。当前使用的自回归RNN(LSTM或者GRU)隐藏层状态 h t h_t ht通过上个时间步中可以观察到的 x t − 1 x_{t-1} xt−1和 x t − 1 x_{t-1} xt−1的协变量 c t − 1 c_{t-1} ct−1(如图1所示):
h t = R N N ( c o n c a t ( x t − 1 , c t − 1 , h t − 1 ) ) ( 3 ) \begin{aligned} h_t=RNN(concat(x_{t-1},c_{t-1},h_{t-1})) \\ (3) \end{aligned} ht=RNN(concat(xt−1,ct−1,ht−1))(3)
这个模型是自回归的模型,因为使用到了上一个时间步的观察值 x t − 1 x_{t-1} xt−1和循环网络的状态 h t − 1 h_{t-1} ht−1,以此计算出当前的观察值 h t h_t ht。
为了得到一个功能强大的生成分布模型,我们将K层流模型(Real NVP或者MAF)堆叠起来。结合RNN,通过给出的历史观察值 t ∈ [ 1 , t 0 ) t \in [1,t_0) t∈[1,t0)和全量的协变量 t ∈ [ 1 , T ] t \in [1,T] t∈[1,T]我们得到了所有时间序列未来的条件分布模型。既然这个模型是自回归的,那么密度函数可以重写为:
p X ( x t 0 : T : x t 1 : t 0 , c t 1 : T ) = ∏ i = 1 D p X ( x t : h t ; θ ) ( 4 ) \begin{aligned} p \mathcal X(x_{t_0:T}:x_{t_1:t_0},c_{t_1:T})=\prod_{i=1}^D p \mathcal X(x_t:h_t;\theta) \\ (4) \end{aligned} pX(xt0:T:xt1:t0,ct1:T)=i=1∏DpX(xt:ht;θ)(4)
θ \theta θ表示所有参数的集合,包括RNN的参数和流的参数
为了模拟时间演化,我们还使用注意力模块进行了研究(Vaswani等人,2017)。这用于计算 t 0 t_0 t0之前的时间序列的embedding。如上所述,训练时间序列被分成预热或编码部分 x 1 : t 0 − 1 x_{1:t_0-1} x1:t0−1和输出部分 x t 0 : T x_{t_0:T} xt0:T。在本例中,有关整个模型的示意图,请参见图2。在训练时,必须注意防止使用来自未来时间点的信息,并通过使用一个反映进展时间因果方向的掩模(即遮住未来时间点)来保持自回归特性。
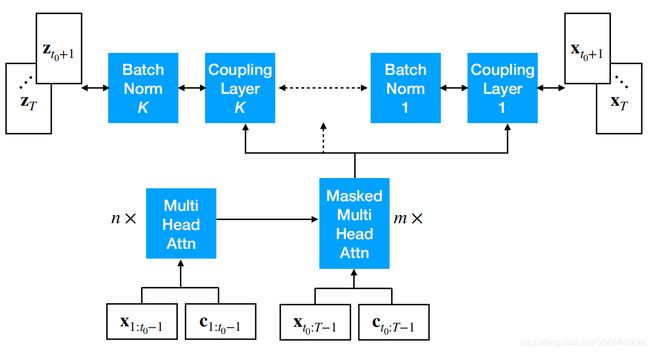
图2. Transformer Conditioned Real NVP模型示意图,包括一个编码器-解码器堆栈,其中编码器获取时间序列中数个上下文长度的子序列,然后通过因果屏蔽解码器栈生成符合条件长度的时间序列预测值。译码器的输出被用作训练流的输入。注意,位置编码是协变量的一部分,与RNN模型不同,这里所有的时间点 x 1 : T x_{1:T} x1:T都是并行训练的。
在现实世界的数据中,不同时间序列的值的大小可能会有很大的变化。为了将时间序列归一化,我们在将数据送入模型前会将时间序列除以它的期望。而输出乘上期望还原为未缩放的值,这种简化的缩放方法,在实际操作中有很好的表现(Salinas等人 (2019b))。
4.1 训练
给定数据集 D D D(一个批次的时间序列),对于每个时间序列和时间步,有 x ∈ R D x \in R^D x∈RD以及协变量 c t c _t ct,在考虑条件化流和RNN或转化器的参数集合的条件下,通过Adam(Kingma & Ba, 2015)给出的SGD(梯度下降)求解(1)式和(3)式的极大似然方程组
L = 1 ∣ D ∣ T ∑ X 1 : t ∈ D ∑ t = 1 T l o g p X ( x t : h t ; θ ) \mathcal L = \frac 1 {|D|T} \sum_{X_{1:t} \in D} \sum_{t=1}^Tlogp \mathcal X(x_t:h_t;\theta) L=∣D∣T1X1:t∈D∑t=1∑TlogpX(xt:ht;θ)
实际上,批次D中的时间序列是从我们训练数据中大小为T的时间窗口中随机选择的,并且相对时间步长保持恒定。这允许模型仅在给定协变量的情况下进行冷启动学习。当用于训练的历史数据较少时,这会增大训练数据集,并允许我们在计算时间和内存消耗之间进行权衡,尤其是在D或T较大时。请注意,有关绝对时间的信息仅可通过协变量提供给RNN或转换器,而不能通过训练数据获得的相对位置。与RNN为相比 O ( T D 2 ) O(TD^2) O(TD2),转换器的计算复杂度为 O ( T 2 D ) O(T^2D) O(T2D),其中T为时间序列长度,并假设隐藏状态的维数与建模的协时间序列的数量成比例地增长。这意味着对于较大的多元时间序列,即 D > T D>T D>T,Transformer流模型的计算复杂度较小。此外,与RNN不同,所有用于训练的计算都是并行进行的。转换器允许模型访问历史时间序列的任何部分,而与时间跨度无关,从而能够为规范化流生成更好的条件。
4.2 协变量
我们提供了分类特征的embeddings,在训练模型的时候可以识别一个分类内部的关系或者分类的上下文关系。将这些embedding作为时间序列预测的特征进行组合,可以产生强大的模型,比如Kaggle第一届出租车轨迹预测挑战赛的冠军(DeBrébisson
等人,2015)。我们使用的协变量由时间相关的(例如,星期几,一天中的小时)和时间无关的embedding(如果适用)以及滞后特征组成,后者取决于用于训练的数据集的时间频率。
在我们希望预测的时间段内,必须知道所有协变量。
4.3 推断
为了进行推断,我们要么通过RNN传递一个“热身”时间序列 x 1 : t − 1 x_{1:t-1} x1:t−1来获得隐藏状态 h ^ t 1 \hat h_{t_1} h^t1,要么使用冷启动即 h ^ t 1 = h 1 = 0 ⃗ \hat h_{t1}=h_1=\vec 0 h^t1=h1=0设置的隐藏状态,然后对噪声向量进行采样(各向同性高斯分布),基于起始状态,通过回流计算,获取下一个时间步的时间序列样本。然后,我们使用该样本及其协变量通过RNN获得下一个条件状态 h ^ t 1 + 1 \hat h_{t_1+1} h^t1+1,重复此步骤,直到达到需要我们推断的时间窗口。从某个初始状态进行采样的过程可能重复很多次,从而获得任意长时间预测范围内我们的预测区间经验分位数。
注意力模型类似地使用预热时间序列 x 1 : t 1 − 1 x_{1:{t_1-1}} x1:t1−1及相应协变量并用编码器编码,然后使用解码器输出条件以从流中进行采样。然后,此样本再次在解码器中使用,以迭代方式采样下一个条件状态,类似于seq-to-seq模型中的推理过程。
5.实验
在这里,我们用实验数据集和6个现实中的生产数据对模型及结果进行了检验分析。
5.1 管道系统中的仿真流
在此实验中,我们通过模拟带有阀门的管道系统中的液体流动来检查模型的一些基本属性。
有关系统的描述,请参见图3。
图3 带有传感器(S)和阀门(V)的液体从左向右流动的管道系统
水流从左到右,这个系统中第一个传感器的压力为 S 0 = X + 3 , X ∼ G a m m a ( 1 , 0.2 ) S_0= X + 3,X \sim Gamma(1,0.2) S0=X+3,X∼Gamma(1,0.2)
。阀门 V 1 , V 2 ∼ i i d B e t a ( 0.5 , 0.5 ) V_1,V_2 \sim _{iid} Beta(0.5,0.5) V1,V2∼iidBeta(0.5,0.5),因此有
S i = V i V 1 + V 2 S 0 + S 1 S_i=\frac {V_i} {V_1+V_2}S_0+S_1 Si=V1+V2ViS0+S1
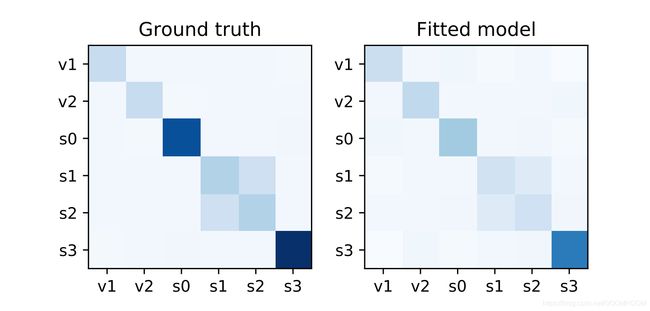
其中 i ∈ 1 , 2 S 3 = S 1 + S 2 + ε 3 ε ∼ N ( 0 , 0.1 ) i \in {1,2} \quad S_3=S_1+S_2+\varepsilon_3 \quad \varepsilon \sim N(0,0.1) i∈1,2S3=S1+S2+ε3ε∼N(0,0.1) 。通过此模拟,我们检查我们的模型是否能捕获时间上的相关性和空间上的相关性。 S 1 S_1 S1和 S 2 S_2 S2之间的相关性是由于两者具有相同的来源(由 S 0 S_0 S0测得)。 这由 C o v ( S 1 , S 2 ) > 0 Cov(S1,S2)\gt 0 Cov(S1,S2)>0反映出来,该值由我们的模型捕获。
图4.某个时间点捕获到的S1和S2的相关系数的协方差矩阵。颜色越深代表正相关程度越高。
实际情况下连续时间点之间的互协方差结构,以及我们训练模型捕获的交叉协方差结构,如图5所示。它反映了系统中液体的真实流量, t t t时刻到达 S 0 S_0 S0, t + 1 t + 1 t+1到达的 S 1 S_1 S1和 S 2 S_2 S2。 t + 2 t + 2 t+2时刻到达 S 3 S_3 S3。

图5. 管道系统中的真实液体流量连续时间点之间的互协方差矩阵。颜色越深代表正相关程度越高。
5.2 生产数据
为了评价模型效果我们在每个单独的时间序列上计算连续分级概率评分( C R P S CRPS CRPS),针对合计值也进行相同操作(稍后会标记为 C R P S s u m CRPS_{sum} CRPSsum)。 C R P S CRPS CRPS度量累积分布函数 F F F与观测值 x x x的相容性
C R P S ( F , x ) = inf R ( F ( z ) − I { x ≤ z } ) ( 5 ) \begin{aligned} CRPS(F,x)=\inf_R(F(z)-\Bbb I\{x \le z\}) \\ (5) \end{aligned} CRPS(F,x)=Rinf(F(z)−I{x≤z})(5)
其中: I I { x ≤ z } \Bbb II\{x \le z\} II{x≤z}是指示函数(当 x ≤ z x \le z x≤z时值为1,否则取0)。 C R P S CRPS CRPS是一个合适的评分函数,因此,当预测分布F和数据分布相同时, C R P S CRPS CRPS达到最小值。利用 F F F的经验函数 C D F CDF CDF,例如将
F ^ ( z ) = 1 n ∑ i = 1 n I ( X i ≤ z ) 其 中 n 个 样 本 X i ∼ F \hat F(z)=\frac 1 n \sum_{i=1}^n \Bbb I(X_i \le z) \quad 其中n个样本X_i \sim F F^(z)=n1i=1∑nI(Xi≤z)其中n个样本Xi∼F
作为预测CDF的自然近似,在每个时间点可以从条件分布的模拟样本中直接计算出CRPS(Jordan等人,2019)(4)。在实践中,我们以100个样本来估算经验CDF。 C R P S s u m CRPS_sum CRPSsum是D个时间序列的和,真实数据和样本数据均如此(就是生成每个时间点的 F ^ s u m ( t ) \hat F_{sum}(t) F^sum(t))。在预测时间窗口中结果取均值,一般地
C R P S s u m = E t [ C R P S ( F ^ s u m ( t ) , ∑ i x t i ) ] CRPS_{sum}=E_t[CRPS(\hat F_{sum}(t),{\sum}_ix_t^i)] CRPSsum=Et[CRPS(F^sum(t),∑ixti)]
模型使用每个数据集的训练数据片训练,对于测试,从训练数据集中最后一个点开始的滚动窗口预测,并将其与测试集进行比较。

表-1.来自alinas等人的模型(2019a)和我们的模型GRU-Real-NVP,GRU-MAF和Transformer-MAF测试集中的比较(越低越好)。两种最佳方式以粗体显示,其中的值均是相应方式运行3次的平均值和标准误差。

表-2. 实验数据集属性
我们在Exchange(Lai等人,2018),Solar(Laiet等人,2018),Electricity2,Traffic3,Taxi4和Wikipedia5开放数据集上进行训练,完全按照Salinas等人的方法进行处理。
(2019a),其属性在表2中列出。Taxi和Wikipedia都由计数数据组成,因此在被馈送到流之前已被量化(并按均值缩放)。
训练参数如下:
batch_size=32
batch_count_per_epoch=100
max_epoch=40
learning_rate=1e-3
这些LSTM/GRU的超参数来自Salinas等人(2019a),nomalizing flow双射的栈数K=3或K=5。验证评估采样次数为100。转换器采用如下参数
H=8
encoding_layer_num=3
decoding_layer_num=3
dropout_rate=0.1
没有对其他的超参数进行调参。所有的实验均是使用单个节点的Nvidia V-100GPU进行的,在审查通过之后,将提供用于重现结果的代码。
我们比较了使用GRU和两种不同规范化流的方法(分别基于Real NVP和MAF的GRU-Real-NVP和GRU-MAF)以及具有MAF的Transformer模型(Transformer-MAF),以及基于RNN的不同方法和Salinas等人(2019a)的变换方案并在表1中报告了结果。Vec-LSTM-ind-scaling通过均值换算输出独立正态分布的参数,Vec-LSTM-lowrank-Copula通过Copula过程参数化了低秩对角协方差矩阵。GP缩放在重建联合分布之前先对每个时间序列进行缩放,然后再对LSTM进行展开,同样,GP-Copula在每个时间序列上对LSTM进行展开,然后通过低秩加对角协方差高斯copula给出联合发散分布。
在表1中,我们观察到具有RNN或时态条件注意机制的MAF在所有数据集上的 C R P S s u m CRPS_{sum} CRPSsum都达到了目前最先进的水平(据我们所知)。此外,与表1的前四列中列出的最新技术水平相比具有RNN的双向流也表现更好。在补充材料中进一步给出了其他评价指标(例如MSE)的分析。
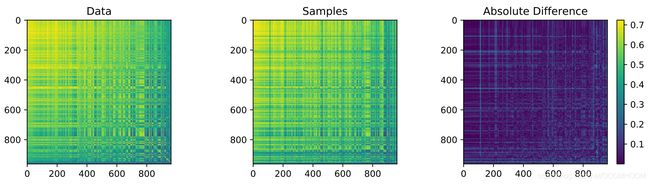
图-6.模型的依赖结构预测分析。左:根据Traffic测试数据集数据片真实值计算的互协方差矩阵。中间:互协方差矩阵是根据Transformer-MAF模型预测值的100个样本轨迹的平均值计算出来的。右图:两个矩阵的绝对差主要显示了真实值和预测值之间的小偏差。
为了评估我们模型的预测性能,我们在图6中绘制了观测值的互协方差矩阵(左图)以及绘制的100个在Traffic测试数据集数据片上Transformer-MAF模型预测值样本轨迹的平均值(中间图)。 图中最右边的图说明了两个互协方差矩阵之间的绝对差。可以看出,大多数协方差结构,尤其是高度相关传感器的左上角区域,从模型中提取的样本中都很好地反映了。
6. 结论
我们提出了一种针对高维的基于概率的多变量时间序列的通用建模方法。这种方法核心是将自回归模型(比如RNN或者注意力机制模型)和条件正则化流相结合。自回归的模型在时间序列预测方面一直有很好的声誉。另一方面,流模型不事先假定先验分布的类型,而是可以适应各种高维数据分布。该组合将自回归类模型的预测能力与流模型的概率密度估计的灵活性相结合。由于不需要进行近似值(协方差结构的低秩近似)重排序,因此效率更高。在没有进行很多超参数调参的情况下,本模型在6个基准数据集上拥有目前国际上最好的表现。
容易想到的一个改进我们这个模型的方法是找到一个更好的潜在流模型。例如,表1显示将Real NVP流与MAF交换可以改善性能,与MAF相比,Real NVP序列模型概率密度建模性能不佳。同样,我们希望其他人设计可供选择的流模型来改善当前方法的性能,例如更改反量化方法,特定仿射耦合层或其他更有效的方法,例如通过另一种Transformer。流模型最新的进展(例如Flow ++(Ho等人2019)所述,以获得表达性二分流模型或处理离散分类数据的模型(Tran等人2019)),我们以后再做可用性的研究。据我们所知,如何通过流对离散的序列数据建模仍然是一个悬而未决的问题-这将最好地体现某些数据集(例如销售数据)的性质。
另外,我们希望改进时间演化模块以改善预测。例如,最近对Transform的改进Reformer(Kitaev等,2020)可以提高存储效率。我们将这些改进留给以后的研究。
最后,现实世界中的应用可能需要训练大量交互时间序列D,例如在电子商务的销售建模中,其中D可以达到数百万或更多。流模型已成功应用于图像建模,这可与这种设置中面临的瞬时维数相提并论,但是对于大时间序列而言,内存需求变得不可行。在以后的工作中,我们将研究可扩展的时间序列模型训练的机制,例如通过对时间序列进行二次采样。