多分类问题
在前面介绍了二分类问题,逻辑回归可以很好的解决二分类问题。但是在现实生活中,存在着大量的多分类问题。
下面就以鸢尾花数据集来学习如何实现多分类的任务。
1、自然顺序码、独热编码、独冷编码
在鸢尾花数据集中一共有三种鸢尾花,分别被标记为 0、1、2,这种编码方式称为自然顺序码,

使用自然顺序码会出现一个奇怪的现象,山鸢尾和维吉尼亚鸢尾的平均值((0+2)/ 2 = 1)就是变色鸢尾。而且他们之间的距离也不同,2 到 0 的距离要远一些,2 到 1 的距离要近一些。这是因为0、1、2这三个数字之间本身就有大小关系。
但是,鸢尾花的类别之间是平等的,并没有谁大一些、谁小一些之分。
目前,大部分机器学习算法都是基于欧氏空间中的度量来进行计算的,使用自然顺序码就有可能在机器学习的过程中造成偏差,为了使得这种非偏序关系的数据取值不具有偏序性,并且到原点的距离是相等的,可以采用独热编码(独热:就是只有一个元素值是1)。
每种类别用一个一维数组来表示。属于哪个类别,对应的元素就是1,其他的元素为0。
显然,采用独热编码需要占用更多的空间,但是它能够更加合理地表示数据之间的关系。它将一维空间中三个标量的点扩展到三维空间中。其中的每一个点到原点的距离都是相等的。采用独热编码,可以有效地避免学习过程中的偏差,因此在机器学习中通常会将离散的特征以及多分类问题中的类别标签采用读热编码的方式来表示。

除此之外,还有独冷编码,它和独热编码相反,就是向量中只有一个元素为0,其他元素都为1。

2、多分类问题
在逻辑回归中,输入特征的线性组合通过 Sigmoid 函数,转化为一个 0 到 1 之间的概率值。

这里的输入x1 和 x2 是样本的两个特征,令 x0 =1,用 w0 表示偏置项,这个分类器可以看成是有三个输入特征。
在多分类问题中,样本的标记常常被表示为采用独热编码的形式,相应的模型的输出也被表示为向量的形式,其中的每个元素是样本属于哪个类别的概率。

例如,上面的这个输出表明样本分别属于三种类别的概率。显然可以判断出来,这个样本属于第三类。
例如:使用属性花瓣长度和花瓣宽度,构造分类器,能够识别 3 种类型的鸢尾花。
要把三种类型的鸢尾花区分开来,就需要构造三个线性模型。

它们有各自不同的系数,现在我们需要寻找一个函数,通过它能够把线性模型的结果 z1 、z2 、z3 转变为属于每个类别的概率。这些概率的和应该等于1。这个函数就是 softmax 函数。
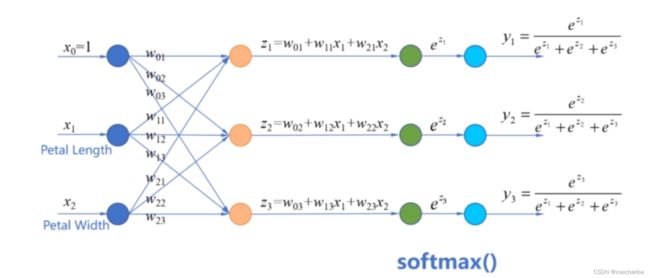
它首先将线性组合 z1、z2 、z3 分别作为自然常数 e 的指数,进行指数运算。这样就显著地拉开了他们之间的差距。使得大数变得更大,小数更小。最后,把它们的和作为分母,对输出进行归一化。这样就保证了 y1、y2 、y3 的值都在0到1之间。并且它们的和等于1,即 y1+y2 +y3 = 1 。
例如当,softmax 函数的输入是 1、2、3 时,指数运算的结果相应为 2.7、7.3、20。在归一化之后,输出的结果为 0.09、0.24、0.67。
属于第三类的概率,明显高于其他两类,如果把第三个数稍微改大一点,变成 5,那么 softmax 函数的输出结果是 0.02、0.05 和 0.93,可以看到,输入值的差距会非常显著地体现在输出概率上,使得最大的那个数以压倒性的优势概率被选出来,之所以称为 softmax,可以理解为以更加 soft 的方式标记出最大的数,这个 soft 是和 hard 对应的。
例如:下面,
import numpy as np
print(np.max([1, 2, 5]))
# 5
print(np.argmax([1, 2, 5]))
# 2
使用 max 函数,就会找到最大数5,而使用 argmax 函数就会找到最大数的索引,其他的数一点机会也没有。成为最大数的概率是0。最大的这个数概率是百分之百,上面这两种就是采用 hard 的方式找到最大值。
而在 softmax 中,标记出的是每个数作为最大值的概率,而不是简单地划分为1和0。除了最大的数,还可以看到其他数的概率,这和使用 Sigmoid 函数代替 step 的概率是类似的。
这些权值构成模型参数矩阵,

这种多分类模型,也称为 softmax 回归,
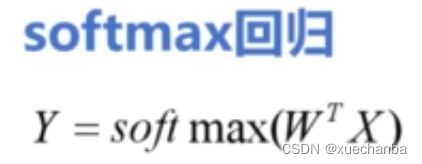
和逻辑回归一样,softmax 回归也是一种广义线性回归,用来完成分类任务,也可以把这些运算合并在一起,以更加简洁的形式来表示,如下图所示。
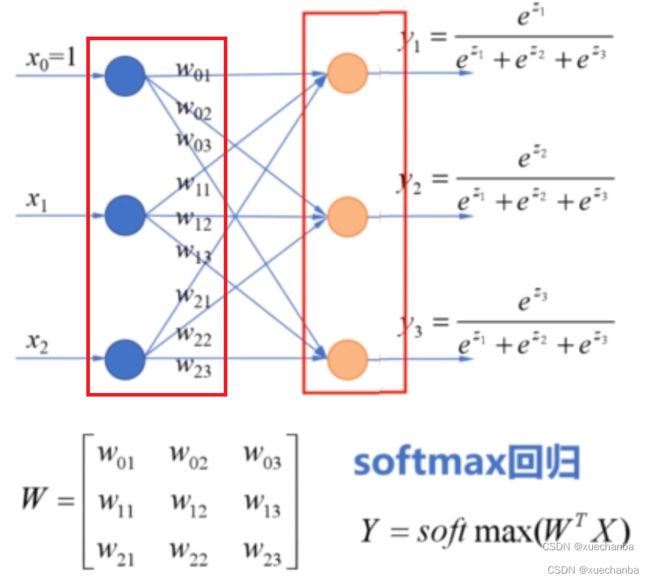
如果要使用鸢尾花数据集中的全部四个属性,作为分类器的输入,加上偏置项w0,一共5个输入项,划分为三类,
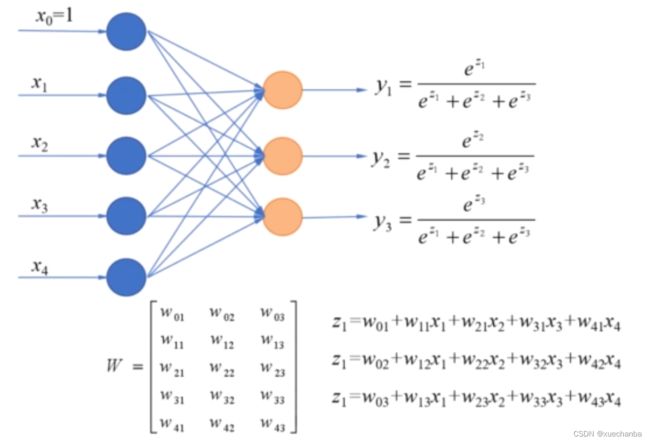
所以输出还是三项,分别对应三个类别的概率,每一个输出,都接收这五个输入的特征,这个模型参数矩阵就是五行三列的,一共有15个权值。这些特征的线性组合经过softmax函数,输出样本属于哪个类别的概率。
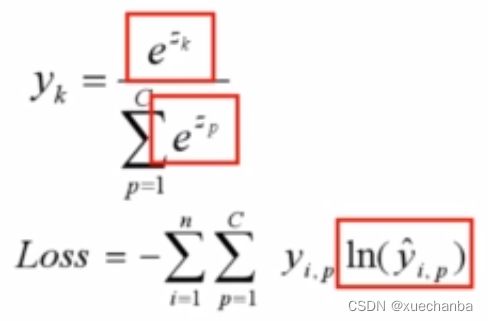
如果把 softmax 推广到一般形式,它的表达式如下:

在鸢尾花的例子中, C 等于 3,k 分别是 1、2、3,softmax 函数是对数几率函数在多分类问题上的推广,可以认为对数几率函数是 softmax 的一个特例。
在二分类问题上,使用二元交叉熵损失函数,

来计算预测值和标签值之间的误差。模型需要预测的结果只有两种情况,所以每个样本有两项相加,样本属于每个类别的预测概率为(y尖)和(1- y尖),对应的标签为 y 和 1- y。
多分类任务是对二分类的扩展,使用多分类交叉熵损失函数,

其中,C 代表样本类别总数,有几个类别,每个样本就有几项相加。当 C 等于 2 时,就是二元交叉熵损失函数。
通过交叉熵损失函数,可以计算概率的损失,也就是预测概率和实际分类标签的误差。交叉熵越小,两个概率分布就越接近(分类越准)。
除此之外,softmax函数和交叉熵损失函数配合使用,
在计算损失函数梯度时,其中的 e 的对数运算和 e 的指数运算可以相互抵消,使得模型的训练更加的简单。因此,在分类问题上,通常采用交叉熵损失函数。
在鸢尾花数据集中,假设我们分别设计两个模型,

从上图可以看到,模型 A 对样本 1 和样本 2 以非常微弱的优势判断正确,而对于样本3来说,判断彻底错误,模型 B 对样本1和样本2的判断非常准确。对样本3判断错误。但是相对来说,没有错的太离谱。这两个模型都是预测错了一个样本,他们的分类准确率都是 2/3 ,但是,模型B表现的很好。
下面,分别来计算两个模型的交叉熵损失。

在使用softmax函数实现的多分类模型中,每个样本只能属于一个类别,这称为互斥的多分类问题。而将一个样本可以同时属于多个类别,称为非互斥的多分类问题。例如,一个图片可能同时被打上多个标签,也就是说一个样本可以同时存在于多个类别中。

对于非互斥的多分类问题,可以通过构建多个一对多的逻辑回归来实现。