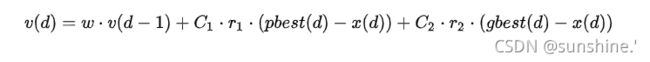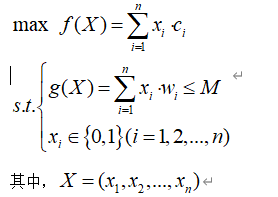##智能优化算法复习--粒子群算法(PSO)
目前常见的群体智能优化算法主要有如下几类:
(1)蚁群算法(Ant Colony Optimization,简称ACO)[1992年提出];
(2)粒子群优化算法(Particle Swarm Optimization,简称PSO)[1995年提出](简单易于实现,也是目前应用最为广泛的群体智能优化算法);
(3)菌群优化算法(Bacterial Foraging Optimization,简称BFO)[2002年提出];
(4)蛙跳算法(Shuffled Frog Leading Algorithm,简称SFLA)[2003年提出];
(5)人工蜂群算法(Artificial Bee Colony Algorithm,简称ABC)[2005年提出];
除了上述几种常见的群体智能算法以外,还有一些并不是广泛应用的群体智能算法,比如萤火虫算法、布谷鸟算法、蝙蝠算法以及磷虾群算法等等。
下面来主要介绍使用最多的粒子群算法
首先来介绍其原理:
在PSO中,每个优化问题的解都是搜索空间中的一只鸟,称之为"粒子",而问题的最优解就对应于鸟群中寻找的食物。所有的粒子都具有一个位置向量(粒子在解空间的位置)和速度向量(决定下次飞行的方向和速度),并可以根据目标函数来计算当前的所在位置的适应值(fitness value),可以将其理解为距离食物的距离。在每次的迭代中,种群中的例子除了根据自身的经(历史位置)进行学习以外,还可以根据种群中最优粒子的"经验"来学习,从而确定下一次迭代时需要如何修正和改变飞行的方向和速度。就这样逐步迭代,最终整个种群的例子就会逐步趋于最优解。
举个简单的鸟群例子看一看
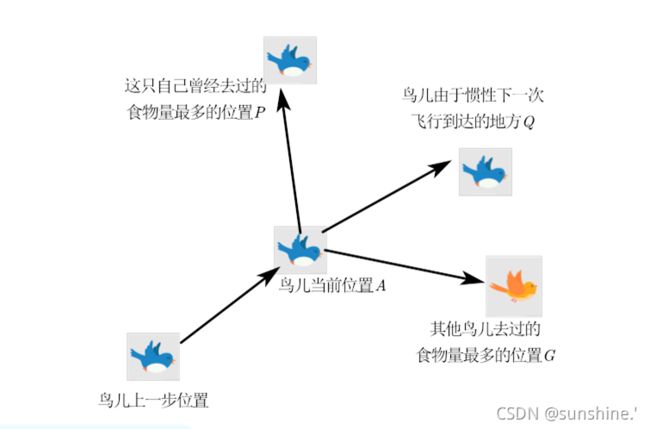
现在,我们的主角是一群鸟。小鸟们的目标很简单,要在这一带找到食物最充足的位置安家、休养生息。试着想一下一群鸟在寻找食物,在这个区域中只有一只虫子,所有的鸟都不知道食物在哪。但是它们知道自己的当前位置距离食物有多远,同时它们知道离食物最近的鸟的位置。
想一下这时候会发生什么?
鸟A:哈哈哈原来虫子离我最近!
鸟B,C,D:我得赶紧往 A 那里过去看看!同时各只鸟在位置不停变化时候离食物的距离也不断变化,所以一定有过离食物最近的位置,这也是它们的一个参考。
鸟某某:我刚刚的位置好像靠近了食物,我得往那里靠近!
(鸟类的这几种想法是粒子群算法的核心)有了这样的想法,它们在这个地方的搜索策略如下:
- 每只鸟随机找一个地方,评估这个地方的食物量。
- 所有的鸟一起开会,选出这群鸟遇到的食物量最多的地方作为安家的候选点G,我们也可以称候选点G为群体中的鸟儿去过的食物量最多的位置
- 每只鸟回顾自己的旅程,记住自己曾经去过的食物量最多的地方P。
- 每只鸟为了找到食物量更多的地方,于是向着G飞行,但是呢,不知是出于选择困难症还是对P的留恋,或者是对G的不信任,小鸟向G飞行时,时不时也向P飞行,其实它自己也不知道到底是G的食物多还是向P的食物多。毕竟G和P方向的食物都比较多,
- 另外还考虑鸟儿飞行的惯性,也就是鸟儿无法立即停下来,由于惯性它会下一次飞行到达点Q
- 又到了开会的时间,如果小鸟们决定停止寻找,那么它们会选择当前的G来安家;否则继续2->3->4->5->6来寻找它们的栖息地。
假如现在我们就是那只鸟,决定向着P和G飞行,因为那里食物多。但是因为存在惯性,我们无法立马停下来,因此还可能朝着另外一个不知名的地方Q飞行,毕竟万一Q的食物多呢?但是我们是佛系鸟,具体飞多少随缘。本该到达地方Q的,但是由于收到P和G两个地方食物的诱惑,它到达不了Q。
最终,我们一定会找到食物最多的地方,因此每一次的寻找,P点和Q点都在不断更新,最后会收敛到食物最多的地方
下面正式进入PSO
现在我们赋予鸟儿一些参数:
- c1:个体学习因子,也称为个体加速因子。这个因子越大,鸟儿越倾向于飞往它自己曾去的食物量最多的地方
- c2:社会学系因子,也成为社会加速因子。这个因子越大,鸟儿越倾向于飞往其他鸟儿(同伴们)曾去的食物量最多的地方
- r1,r2:[0,1]上的随机数。随机代表着鸟儿比较佛系,他也不知道飞哪里
- w:惯性权重,也叫惯性系数,这个数越大,代表着它不容易更改之前的运动路线,更倾向于探索未知领域.
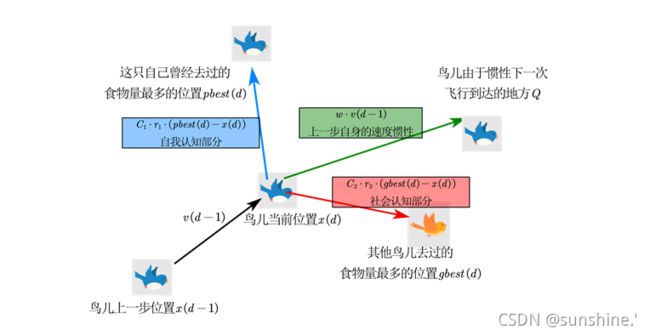
现在图像就变成了这样:
因此这只鸟第d步所在的位置=第d-1步所在的位置+第d-1步所在的位置*运动的时间(每一步运动的时间t一般取1)
这只鸟第d步的速度=上一步自身的速度惯性+自我认知部分+社会认知部分
每运动一次,位置P和Q都会不断发生变化,最后会收敛到一个位置,这个位置就是食物最多的一个位置
再看一下算法流程图
主要步骤:
step1
种群初始化,可以进行随机初始化或者根据被优化的问题设计特定的初始化方法,然后计算个体的适应值,从而选择出个体的局部最优位置向量和种群的全局最优位置向量。
step2
迭代设置:设置迭代次数
step3
速度更新:更新每个个体的速度向量
step4
位置更新:更新每个个体的位置向量
step5
局部位置和全局位置向量更新:更新每个个体的局部最优解和种群的全局最优解
step6
终止条件判断:判断迭代次数时都达到最大迭代次数,如果满足,输出全局最优解,否则继续进行迭代,跳转至step 3。
在粒子群算法里核心公式就是
1.这只鸟第d步的速度=上一步自身的速度惯性+自我认知部分+社会认知部分
2.这只鸟第d+1步所在的位置=第步所在的位置+第步所在的位置*运动的时间(每一步运动的时间t一般取1)
在这其中:个体学习因子和社会学习因子c1,c2取1.5比较合适
w=[0.8-1.2]
下面举一个例子说明一下:
什么是0-1背包问题呢
背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学,计算复杂性理论、密码学和应用数学等领域中。也可以将背包问题描述为决定性问题,即在总重量不超过W的前提下,总价值是否能达到V?它是在1978年由Merkel和Hellman提出的。
其中数学模型如下
已知n个物品的尺寸大小分别为wi(i=1,2,3…,n),它们对应的价值分别为ci(i=1,2,3…,n),背包的最大容量为M。求获得最大价值的物品选择方案。需要说明的是,所有的体积值均为整数,也就是说,每件物品只有取或者不取两种可能性,不可以分解物品。
背包问题的数学模型实际上是一个0-1规划问题。定义xi为0/1变量,即当物品被选入背包时xi=1,否则xi=0。现在考虑这n个物品的选择与否,则背包内n个物品的总重量为
物品的总价值为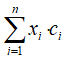 ,同时满足约束条件,总重量不大于背包的最大容量,问题的目标就是要在背包尽量装满但又不超过其容量的情况下,使背包中的物体价值最大。则该背包问题的模型可以表示为:
,同时满足约束条件,总重量不大于背包的最大容量,问题的目标就是要在背包尽量装满但又不超过其容量的情况下,使背包中的物体价值最大。则该背包问题的模型可以表示为:
下面用粒子群算法解决0-1背包问题:
%%%%%%%%%%离散粒子群算法解决0-1背包问题%%%%%%%%%%%
%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
N=100; %群体粒子个数
D=10; %粒子维数
T=200; %最大迭代次数
c1=1.5; %学习因子1
c2=1.5; %学习因子2
Wmax=0.8; %惯性权重最大值
Wmin=0.4; %惯性权重最小值
Vmax=10; %速度最大值
Vmin=-10; %速度最小值
V = 300; %背包容量
C = [95,75,23,73,50,22,6,57,89,98]; %物品体积
W = [89,59,19,43,100,72,44,16,7,64]; %物品价值
afa = 2; %惩罚函数系数
%%%%%%%%%初始化种群个体(限定位置和速度)%%%%%%%%%%
x=rand(N,D); %随机获得二进制编码的初始种群
v=rand(N,D) * (Vmax-Vmin)+Vmin;
%%%%%%%%%%%初始化个体最优位置和最优值%%%%%%%%%%%%
p=x;
pbest=ones(N,1);
for i=1:N
pbest(i)= func4(x(i,:),C,W,V,afa);
end
%%%%%%%%%%%%初始化全局最优位置和最优值%%%%%%%%%%%
g=ones(1,D);
gbest=eps;
for i=1:N
if(pbest(i)>gbest)
g=p(i,:);
gbest=pbest(i);
end
end
gb=ones(1,T);
%%%%%%%按照公式依次迭代直到满足精度或者迭代次数%%%%%%%
for i=1:T
for j=1:N
%%%%%%更新个体最优位置和最优值%%%%%%%%%%%%%
if (func4(x(j,:),C,W,V,afa)>pbest(j))
p(j,:)=x(j,:);
pbest(j)=func4(x(j,:),C,W,V,afa);
end
%%%%%%%%%%更新全局最优位置和最优值%%%%%%%%%
if(pbest(j)>gbest)
g=p(j,:);
gbest=pbest(j);
end
%%%%%%%%%%计算动态惯性权重值%%%%%%%%%%%%%
w=Wmax-(Wmax-Wmin)*i/T;
%%%%%%%%%%跟新位置和速度值%%%%%%%%%%%%%%
v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))...
+c2*rand*(g-x(j,:));
%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%
for ii=1:D
if (v(j,ii)>Vmax) | (v(j,ii)< Vmin)
v(j,ii)=rand * (Vmax-Vmin)+Vmin;
end
end
vx(j,:)=1./(1+exp(-v(j,:)));
for jj=1:D
if vx(j,jj)>rand
x(j,jj)=1;
else
x(j,jj)=0;
end
end
end
%%%%%%%%%%%%%记录历代全局最优值%%%%%%%%%%%%
gb(i)=gbest;
end
g %最优个体
figure
plot(gb)
xlabel('迭代次数');
ylabel('适应度值');
title('适应度进化曲线')
%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%%
function result = func4(f,C,W,V,afa)
fit = sum(f.*W);
TotalSize = sum(f.*C);
if TotalSize <= V
fit = fit;
else
fit = fit - afa * (TotalSize - V);
end
result = fit;
end