QR分解的几何解释,并荐书《Algebra, Topology, Differential, Calculus, and Optimization Theory》
目录
- 一、简介
- 二、QR分解
- 三、基于超平面反射(Hyperplane Reflection)的 QR Decomposition
-
- 3.1 超平面反射映射(Hyperplane Reflection Map)
- 3.2 基于超平面反射的 QR Decomposition 证明
- 四、QR分解的代码实现
- 小结
- 参考文献
一、简介
首先,我在这里推荐一本好书——《Algebra, Topology, Differential, Calculus, and Optimization Theory for Computer Science and Engineering》 【1】 ,该书作者是 Jean Gallier 【2】 教授。老爷子70多岁,就职于宾西法利亚大学 计算机与信息学院,可说本书是他将几十年的教学经验凝聚之精华,总共1900页,分为 9 个大部分,54章,涵盖了线性空间、代数几何、代数、拓扑、微分方程、最优化理论、机器学习等多个方面的数学基础,没有几十年功力实难驾驭自如。书中详细地介绍了计算机科学所需的各门类数学基础,不仅是从本科的基础高等数学到各领域专业前沿研究的重要过渡,也为继续学习更为高深的数学做了一定的铺垫,以及指明了方向。最难得的是,这本大部头是开源的,我把这个资源列在了文章后面的参考文献【1】中,真希望能找到一同学习的同学,可以聊聊学习心得,相互启发、帮助,共同进步。
以下博文是我依据该书第12章(《QR-Decomposition for Arbitrary Matrices》)的内容,结合自己的理解写成,不对之处,还望不吝赐教。
二、QR分解
把矩阵分解为形式比较简单或具有某种特性的一些矩阵的乘积,称之为矩阵分解,它在矩阵理论的研究与应用中占据着非常重要的地位。因为一方面,这些分解式的特殊形式能够反映出原矩阵的某些数值特征;另一方面,这些分解的方法与过程为数值计算提供了理论依据。矩阵 QR 分解是将任意矩阵 A A A 分解为两个矩阵相乘,如: A = Q R A = QR A=QR,其中 Q Q Q 是规范正交矩阵(Orthonormal Matrix), R R R 是上三角矩阵(Upper Triangular Matrix)。QR分解在解决最小二乘问题、特征值计算方面都有广泛应用。【3】
在【4】中,给出了QR分解的一般证明(原书 2.6.1 定理),它是基于 Gram-Schmidt 正交化给出的:
定理1:QR分解
如果 A ∈ M n , m A\in M_{n,m} A∈Mn,m 且 n ≥ m n\ge m n≥m,那么存在具有标准正交列(归一化正交)的矩阵 Q ∈ M n , m Q\in M_{n,m} Q∈Mn,m 和上三角矩阵 R ∈ M m , m R\in M_{m,m} R∈Mm,m,使得 A = Q R A=QR A=QR。如果 n = m n=m n=m,那么 Q Q Q 是酉矩阵(即 Q ∗ Q = Q Q ∗ = I Q^*Q=QQ^*=I Q∗Q=QQ∗=I);此外,如果 A A A 是非奇异矩阵,则可以选取 R R R 为具有正对角元的上三角矩阵,并且在这种情况,因子 Q Q Q 和 R R R 都是唯一的,如果 A ∈ M n , m ( R ) A\in M_{n,m}(\mathbb R) A∈Mn,m(R),那么 Q Q Q 和 R R R 都可以取实矩阵。
证明:
如果 A ∈ M n , m A\in M_{n,m} A∈Mn,m ,且 r a n k ( A ) = m rank(A) = m rank(A)=m,则 A A A 的各列构成 C n \mathbb C^n Cn 的一个无关组,把 Gram-Schmidt 过程应用于 A A A 的各列,用矩阵记号描述所得的结果,就可以得到 A A A 的QR分解。Gram-Schmidt 算法的自然推广使同样的矩阵记号描述能够应用于任意矩阵 A A A 的各列,于是得到一般矩阵 A A A 的QR分解。以下简述之:
设 A = [ a 1 , a 2 , ⋯ , a m ] A=[\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_m] A=[a1,a2,⋯,am],其中 a i \mathbf a_i ai 是 A A A 的列矢量(column vector),对 A A A 的各列矢量执行 Gram-Schmidt 过程,得到正交矢量 p 1 , p 2 , ⋯ , p m \mathbf p_1,\mathbf p_2,\cdots,\mathbf p_m p1,p2,⋯,pm,归一化得到 q 1 , q 2 , ⋯ , q m \mathbf q_1,\mathbf q_2,\cdots,\mathbf q_m q1,q2,⋯,qm,过程如下:
- 正交化过程:
p 1 = a 1 p 2 = a 2 − a 2 T p 1 ∥ p 1 ∥ 2 p 1 p 3 = a 3 − a 3 T p 1 ∥ p 1 ∥ 2 p 1 − a 3 T p 2 ∥ p 2 ∥ 2 p 2 ⋯ ⋯ p m = a m − a m T p 1 ∥ p 1 ∥ 2 p 1 − ⋯ a m T p m − 1 ∥ p m − 1 ∥ 2 p m − 1 \mathbf p_1 = \mathbf a_1 \\ \ \\ \mathbf p_2 = \mathbf a_2 - \frac{\mathbf a_2^T\mathbf p_1}{\Vert\mathbf p_1\Vert^2}\mathbf p_1 \\ \ \\ \mathbf p_3 = \mathbf a_3 - \frac{\mathbf a_3^T\mathbf p_1}{\Vert\mathbf p_1\Vert^2}\mathbf p_1-\frac{\mathbf a_3^T\mathbf p_2}{\Vert\mathbf p_2\Vert^2}\mathbf p_2 \\ \cdots\cdots \\ \mathbf p_m = \mathbf a_m - \frac{\mathbf a_m^T\mathbf p_1}{\Vert\mathbf p_1\Vert^2}\mathbf p_1-\cdots\frac{\mathbf a_m^T\mathbf p_{m-1}}{\Vert\mathbf p_{m-1}\Vert^2}\mathbf p_{m-1} p1=a1 p2=a2−∥p1∥2a2Tp1p1 p3=a3−∥p1∥2a3Tp1p1−∥p2∥2a3Tp2p2⋯⋯pm=am−∥p1∥2amTp1p1−⋯∥pm−1∥2amTpm−1pm−1
- 归一化过程:
q i = p i ∥ p i ∥ \mathbf q_i = \frac {\mathbf p_i}{\Vert\mathbf p_i\Vert} qi=∥pi∥pi
由此
a 1 = p 1 = ∥ p 1 ∥ q 1 = r 11 q 1 a 2 = a 2 T p 1 ∥ p 1 ∥ 2 p 1 + p 2 = r 21 q 1 + r 22 q 2 \mathbf a_1= \mathbf p_1 = \Vert \mathbf p_1\Vert \mathbf q_1=r_{11} \mathbf q_1 \\ \ \\ \mathbf a_2 = \frac{\mathbf a_2^T\mathbf p_1}{\Vert\mathbf p_1\Vert^2}\mathbf p_1 + \mathbf p_2 = r_{21} \mathbf q_1 + r_{22} \mathbf q_2 a1=p1=∥p1∥q1=r11q1 a2=∥p1∥2a2Tp1p1+p2=r21q1+r22q2
其中, r 21 = a 2 T p 1 ∥ p 1 ∥ 2 ⋅ r 11 r_{21} = \frac{\mathbf a_2^T\mathbf p_1}{\Vert\mathbf p_1\Vert^2}\cdot r_{11} r21=∥p1∥2a2Tp1⋅r11 和 r 22 = p 2 ∥ p 2 ∥ r_{22}=\frac {\mathbf p_2}{\Vert\mathbf p_2\Vert} r22=∥p2∥p2,如此类推,可得:
a i = r i 1 q 1 + r i 2 q 2 + ⋯ + r i i q i , 1 ≤ i ≤ m \mathbf a_i=r_{i1}\mathbf q_1+r_{i2}\mathbf q_2 + \cdots+r_{ii}\mathbf q_i \qquad , 1\le i\le m ai=ri1q1+ri2q2+⋯+riiqi,1≤i≤m
于是,
A = [ a 1 , a 2 , ⋯ , a m ] = [ r 11 q 1 , r 21 q 1 + r 22 q 2 , ⋯ , r m 1 q 1 + ⋯ + r m m q m ] = [ q 1 , q 2 , ⋯ , q m ] ⋅ [ r 11 r 21 ⋯ r m 1 0 r 22 ⋯ r m 2 0 0 ⋯ r m 3 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ r m m ] A=[\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_m]\\ =[r_{11}\mathbf q_1,\ r_{21}\mathbf q_1+r_{22}\mathbf q_2,\cdots,\ r_{m1}\mathbf q_1+\cdots + r_{mm}\mathbf q_m]\\ \ \\ =[\mathbf q_1,\mathbf q_2,\cdots,\mathbf q_m]\cdot\left[ \begin{array}{cccc} r_{11}& r_{21}&\cdots& r_{m1}\\ 0& r_{22}&\cdots& r_{m2}\\ 0&0&\cdots& r_{m3}\\ \vdots&\vdots&\ddots& \vdots\\ 0&0&\cdots& r_{mm} \end{array}\right] A=[a1,a2,⋯,am]=[r11q1, r21q1+r22q2,⋯, rm1q1+⋯+rmmqm] =[q1,q2,⋯,qm]⋅⎣⎢⎢⎢⎢⎢⎡r1100⋮0r21r220⋮0⋯⋯⋯⋱⋯rm1rm2rm3⋮rmm⎦⎥⎥⎥⎥⎥⎤
我们得到归一化正交矩阵 Q = [ q 1 , q 2 , ⋯ , q m ] Q=[\mathbf q_1,\mathbf q_2,\cdots,\mathbf q_m] Q=[q1,q2,⋯,qm] 和上三角矩阵
R = [ r 11 r 21 ⋯ r m 1 0 r 22 ⋯ r m 2 0 0 ⋯ r m 3 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ r m m ] R=\left[ \begin{array}{cccc} r_{11}& r_{21}&\cdots& r_{m1}\\ 0& r_{22}&\cdots& r_{m2}\\ 0&0&\cdots& r_{m3}\\ \vdots&\vdots&\ddots& \vdots\\ 0&0&\cdots& r_{mm} \end{array}\right] R=⎣⎢⎢⎢⎢⎢⎡r1100⋮0r21r220⋮0⋯⋯⋯⋱⋯rm1rm2rm3⋮rmm⎦⎥⎥⎥⎥⎥⎤
证毕。
三、基于超平面反射(Hyperplane Reflection)的 QR Decomposition
由 Gram-Schmidt 过程是可以证明QR分解的,但其过程不能很好地揭示矢量空间的几何性质。在【1】中给出一个基于超平面反射下QR分解的证明,整个过程有着清晰的几何变换意义,该证明过程简述如下。
3.1 超平面反射映射(Hyperplane Reflection Map)
首先,我们将建立一个称为投影(Projection)的概念。
定理1:(【1】中 Proposition 5.5)投影映射(Projection Map)
如果 E E E 是任意矢量空间(vector space),对于 E E E 的任意有限维子空间 U 1 , U 2 , ⋯ , U p U_1,U_2,\cdots,U_p U1,U2,⋯,Up,有
E = U 1 ⊕ U 2 ⋯ ⊕ U p E=U_1\oplus U_2\cdots\oplus U_p E=U1⊕U2⋯⊕Up
其中,“ ⊕ \oplus ⊕”表示直和(Direct Sum),因为任意矢量 u ∈ E u\in E u∈E 都可以唯一地表示成为:
u = u 1 + ⋯ + u p u=u_1+\cdots+u_p u=u1+⋯+up
其中, u i ∈ U i , for i = 1 ⋯ , p u_i\in U_i,\ \text{ for } i=1\cdots,p ui∈Ui, for i=1⋯,p,由此,我们可以定义一个被称为投影(Projection)的映射 π i : E → U i \pi_i:E\to U_i πi:E→Ui,具体为:
π i ( u ) = π i ( u 1 + ⋯ + u p ) = u i \pi_i(u)=\pi_i(u_1+\cdots+u_p)=u_i πi(u)=πi(u1+⋯+up)=ui
定义2: 对称映射 Symmetry(或称为反射 Reflection),【1】中 Definition 12.1
给定任意矢量空间 E E E, F F F 和 G G G 是 E E E 中任意可以直和构成 E E E 的子空间,即 E = F ⊕ G E=F\oplus G E=F⊕G,则“平行于 G G G ,关于 F F F ”的反射 Reflection(对称映射 Symmetry)是这样一个映射 s : E → E s:E\to E s:E→E
s ( u ) = 2 p F ( u ) − u , for every u ∈ E s = 2 p F − i d s(u)=2p_F(u)-u,\qquad \text{for every } u\in E \\ s = 2p_F-id s(u)=2pF(u)−u,for every u∈Es=2pF−id
其中, p F ( ⋅ ) p_F(\cdot) pF(⋅)表示关于 F F F 的投影(Projection), i d id id 表示全等映射(Identity Map, i d ( u ) = u id(u)=u id(u)=u),以下 “ ∘ \circ ∘” 表示复合运算,于是有以下等式:
p F ( u ) + p G ( u ) = u p F + p G = i d s 2 = s ∘ s = ( 2 p F − i d ) ∘ ( 2 p F − i d ) = 2 p F ∘ 2 p F − i d ∘ 2 p F − 2 p F ∘ i d + i d ∘ i d = 4 p F − 2 p F − 2 p F + i d = i d s ( u ) = 2 p F ( u ) − u = p F ( u ) − p G ( u ) s = 2 p F − i d = p F − p G p_F(u)+p_G(u)=u \\ p_F + p_G=id\\ \ \\ s^2=s\circ s=(2p_F-id)\circ(2p_F-id)\\ =2p_F\circ 2p_F-id\circ 2p_F - 2p_F\circ id+ id\circ id\\ = 4p_F-2p_F-2p_F+id = id \\ \ \\ s(u)=2p_F(u)-u=p_F(u)-p_G(u)\\ s = 2p_F-id = p_F - p_G pF(u)+pG(u)=upF+pG=id s2=s∘s=(2pF−id)∘(2pF−id)=2pF∘2pF−id∘2pF−2pF∘id+id∘id=4pF−2pF−2pF+id=id s(u)=2pF(u)−u=pF(u)−pG(u)s=2pF−id=pF−pG
在定义2上再加一个约束: F ⊥ G F\bot G F⊥G,则此反射称为正交反射 Orthogonal Reflection(或正交对称 Orthogonal Symmetry)。若再在此基础上加一个约束, F F F 是 E E E 的超平面 Hyperplane,则此关于 F F F 的反射,就称为超平面反射 Hyperplane Reflection。以下给出一个3维实矢量空间 R 3 \mathbb R^3 R3 的超平面反射例子,如下图:

图1 R 3 \mathbb R^3 R3 的超平面反射, R 3 = F ⊕ G \mathbb R^3=F\oplus G R3=F⊕G,其中橙色平面表示 F F F, G G G 正交于 F F F,矢量 u u u 分解为两部分: p F ( u ) , p G ( u ) p_F(u),p_G(u) pF(u),pG(u), u u u 经 F F F 反射后,得到 s ( u ) s(u) s(u)
定义3: Householder Matrix(【1】的 Definition 12.3)
具有以下形式的矩阵,称为 Householder 矩阵
H = I n − 2 ω ω T ∥ ω ∥ 2 H = I_n-2\frac{\omega\omega^T}{\Vert \omega\Vert^2} H=In−2∥ω∥2ωωT
其中, ω ∈ R n \omega\in \mathbb R^n ω∈Rn 是一个非 0 矢量。
若 s ( u ) s(u) s(u) 是关于 H H H,正交于 G G G ( G G G是正交于 H H H的一维矢量空间)的 Hyperplane Reflection,其中 u ∈ R n u\in\mathbb R^n u∈Rn。则由定义2,有:
s ( u ) = 2 p F ( u ) − u = u − 2 p G ( u ) with ω ∈ G , ⇒ p G ( u ) = λ ω ⇒ s ( u ) = u − 2 λ ω s(u) = 2p_F(u)- u = u- 2p_G(u) \\ \text{with } \omega \in G, \Rightarrow p_G(u) = \lambda\omega \\ \ \\ \Rightarrow s(u)=u-2\lambda \omega s(u)=2pF(u)−u=u−2pG(u)with ω∈G,⇒pG(u)=λω ⇒s(u)=u−2λω
又因为:
u = p F ( u ) + p G ( u ) and p F ( u ) ⊥ p G ( u ) u ⋅ ω = ( p F ( u ) + p G ( u ) ) ⋅ ω = p F ( u ) ⋅ ω + p G ( u ) ⋅ ω = 0 + λ ω ⋅ ω = λ ∥ ω ∥ 2 ⇒ λ = u ⋅ ω ∥ ω ∥ 2 ⇒ s ( u ) = u − 2 u ⋅ ω ∥ ω ∥ 2 ω = I n u − 2 ∥ ω ∥ 2 ω ( ω T u ) = ( I n − 2 ω ω T ∥ ω ∥ 2 ) u = H u ) ⇒ H = I n − 2 ω ω T ∥ ω ∥ 2 u=p_F(u)+p_G(u) \text{ and } p_F(u) \bot p_G(u) \\ \ \\ u\cdot\omega=(p_F(u)+p_G(u))\cdot\omega\\ =p_F(u)\cdot \omega+p_G(u)\cdot\omega\\ =0+\lambda \omega\cdot \omega = \lambda\Vert \omega\Vert^2 \\ \ \\ \Rightarrow\lambda = \frac {u\cdot \omega}{\Vert \omega\Vert^2} \\ \ \\ \Rightarrow s(u)=u-2\frac {u\cdot \omega}{\Vert \omega\Vert^2} \omega \\ \ \\ =I_nu-\frac 2{\Vert \omega\Vert^2}\omega(\omega^Tu)\\ \ \\ =(I_n-2\frac{\omega\omega^T}{\Vert \omega\Vert^2})u=Hu)\\ \ \\ \Rightarrow H=I_n-2\frac{\omega\omega^T}{\Vert \omega\Vert^2} u=pF(u)+pG(u) and pF(u)⊥pG(u) u⋅ω=(pF(u)+pG(u))⋅ω=pF(u)⋅ω+pG(u)⋅ω=0+λω⋅ω=λ∥ω∥2 ⇒λ=∥ω∥2u⋅ω ⇒s(u)=u−2∥ω∥2u⋅ωω =Inu−∥ω∥22ω(ωTu) =(In−2∥ω∥2ωωT)u=Hu) ⇒H=In−2∥ω∥2ωωT
上式中“ ⋅ \cdot ⋅”表示矢量的点积,点积可以化为矢量相乘,矢量乘满足结合律,另外,标量左乘矢量等于标量右乘矢量,即: ( u ⋅ ω ) ω = ω ( u ⋅ ω ) (u\cdot\omega)\omega=\omega(u\cdot\omega) (u⋅ω)ω=ω(u⋅ω)。因此:
( u ⋅ ω ) ω = ω ( u ⋅ ω ) = ω ( ω T u ) = ( ω ω T ) u (u\cdot\omega)\omega=\omega(u\cdot\omega)=\omega(\omega^Tu)=(\omega\omega^T)u (u⋅ω)ω=ω(u⋅ω)=ω(ωTu)=(ωωT)u
由上述推导可知,Householder Matrix 实际上就是超平面反射 Hyperplane Reflection 对应的矩阵。
3.2 基于超平面反射的 QR Decomposition 证明
定理的证明分为三个步骤组成:
- 平面反射的存在性和唯一性
- 反射矢量可由部分基矢量线性组合表示
- Q矩阵与R矩阵的形成
这三个步骤其实是三个定理的证明,现摘录如下:
定理2:
平面反射的存在性与唯一性(【1】的 Proposition 12.2)
E E E 是一个非平凡 Euclidean 矢量空间,取它的任意两个等长矢量有
u , v ∈ E , and ∥ u ∥ = ∥ v ∥ u,v\in E,\text{ and }\Vert u \Vert = \Vert v \Vert u,v∈E, and ∥u∥=∥v∥
则存在一个超平面(hyperplane) H H H,该 H H H 能对 u u u 进行超平面反射得到 v v v,若 u ≠ v u\neq v u=v,则这样的超平面反射 H H H 是唯一的。如图2:
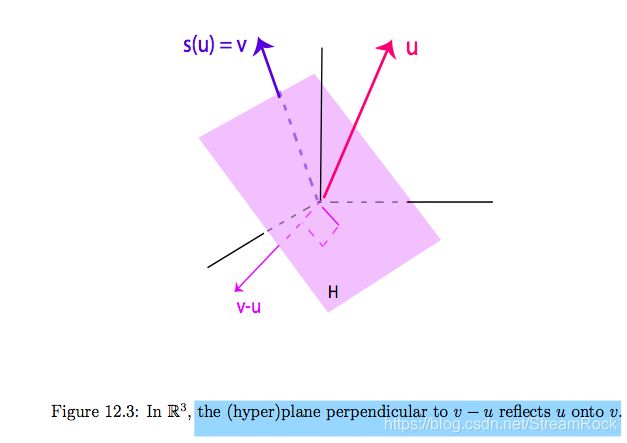
图2、 H H H 是 u , v u,v u,v 的反射平面
证明:
如果 u = v u=v u=v,则任何包含 u , v u,v u,v 的超平面都可以作为反射平面。否则, v − u ≠ 0 v-u\neq 0 v−u=0,则一定存在超平面 Hyperplane H = { v − u } ⊥ H = \{v-u \}^{\bot} H={v−u}⊥,且该平面是唯一的(因为 Hyperplane 超平面是过原点的)。则 u u u 关于 H H H 的反射满足:
s ( u ) = u − 2 ( u ⋅ ( v − u ) ) ∥ ( v − u ) ∥ 2 ( v − u ) = u + 2 ∥ u ∥ 2 − 2 u ⋅ v ∥ ( v − u ) ∥ 2 ( v − u ) s(u)=u-2\frac{(u\cdot(v-u))}{\Vert (v-u)\Vert^2}(v-u)=u+\frac{2\Vert u \Vert^2-2u\cdot v}{\Vert (v-u)\Vert^2}(v-u) s(u)=u−2∥(v−u)∥2(u⋅(v−u))(v−u)=u+∥(v−u)∥22∥u∥2−2u⋅v(v−u)
因为
∥ ( v − u ) ∥ 2 = ( v − u ) ⋅ ( v − u ) = v ⋅ v − u ⋅ v − v ⋅ u + v ⋅ v = ∥ u ∥ 2 + ∥ v ∥ 2 − 2 u ⋅ v \Vert (v-u) \Vert^2=(v-u)\cdot(v-u)=v\cdot v - u\cdot v - v\cdot u + v\cdot v \\ = \Vert u \Vert^2 + \Vert v \Vert^2 - 2u\cdot v ∥(v−u)∥2=(v−u)⋅(v−u)=v⋅v−u⋅v−v⋅u+v⋅v=∥u∥2+∥v∥2−2u⋅v
又因为 ∥ u ∥ = ∥ v ∥ \Vert u \Vert = \Vert v \Vert ∥u∥=∥v∥,因此 ∥ ( v − u ) ∥ 2 = 2 ∥ u ∥ 2 − 2 u ⋅ v \Vert (v-u) \Vert^2=2\Vert u \Vert^2-2u\cdot v ∥(v−u)∥2=2∥u∥2−2u⋅v,所以 s ( u ) = v s(u)=v s(u)=v,证毕。
定理3:(【1】的 Proposition 12.3)
E E E 是 n 维非平凡 Euclidean Space, ( e 1 , ⋯ , e n ) (e_1,\cdots,e_n) (e1,⋯,en) 是它的一个规范正交基(Orthonormal Basis), ( v 1 , ⋅ , v n ) (v_1,\cdot,v_n) (v1,⋅,vn) 是由 E E E 中 n 个任意矢量构成的 n 元组(n-tuple),则存在 n 个等距变换(Isometries) h 1 , ⋯ , h n h_1,\cdots,h_n h1,⋯,hn, h i h_i hi 可以是一个超平面反射(Hyperplane Reflection)或者是全等映射(Identity),使得,若 n 元组 ( r 1 , ⋯ , r n ) (r_1,\cdots,r_n) (r1,⋯,rn) 中每一个矢量都来自复合映射
r j = h n ∘ ⋯ ∘ h 1 ( v j ) r_j=h_n\circ\cdots\circ h_1(v_j) rj=hn∘⋯∘h1(vj)
则每个 r j r_j rj 皆可由下标不大于 j 的基矢量 ( e 1 , ⋯ , e j ) , 1 ≤ j ≤ n (e_1,\cdots,e_j), 1\le j \le n (e1,⋯,ej),1≤j≤n 线性表示,即
r j = λ 1 e 1 + ⋯ + λ j e j , 1 ≤ j ≤ n r_j = \lambda_1e_1+ \cdots +\lambda_j e_j,\ 1\le j \le n rj=λ1e1+⋯+λjej, 1≤j≤n
这样,由 r j r_j rj 作为列矢量的矩阵 R R R 在基 ( e 1 , ⋯ , e n ) (e_1,\cdots,e_n) (e1,⋯,en) 上就是一个上三角矩阵(Upper Triangular Matrix),而且,我们还可以通过选择 h i h_i hi 使 R R R 的对角元素是非负实数(nonnegative)。
证明:
该定理的证明可采用递推法(Induction)证明。
第一步,我们令 E E E 的维数是 n = 1 n=1 n=1,由此有 v 1 = λ e 1 , λ ∈ R v_1 = \lambda e_1,\lambda \in \mathbb R v1=λe1,λ∈R。如果 λ ≥ 0 \lambda \ge 0 λ≥0,令 h 1 = i d h_1 = id h1=id,否则, λ < 0 \lambda \lt 0 λ<0,令 h 1 = − i d h_1= -id h1=−id,则定理成立,此反射是关于原点反射。
第二步,对于 n ≥ 2 n\ge 2 n≥2,首先,我们需要找出 h 1 h_1 h1。
令
r 1 , 1 = ∥ v 1 ∥ r_{1,1} = \Vert v_1 \Vert r1,1=∥v1∥
如果 v 1 = r 1 , 1 e 1 v_1 = r_{1,1}e_1 v1=r1,1e1,我们则令 h 1 = i d h_1=id h1=id。否则,必存在一个唯一的 超平面反射(hyperplane reflection) h 1 h_1 h1 使
h 1 ( v 1 ) = r 1 , 1 e 1 h_1(v_1) = r_{1,1}e_1 h1(v1)=r1,1e1
即在基矢量 e 1 e_1 e1 与 v 1 v_1 v1 之间存在一个超平面反射 h 1 h_1 h1,有:
h 1 ( u ) = u − 2 ( u ⋅ ω 1 ) ∥ ω 1 ∥ 2 ω 1 ω 1 = r 1 , 1 e 1 − v 1 h_1(u)=u-2\frac{(u\cdot \omega_1)}{\Vert \omega_1 \Vert^2}\omega_1 \\ \omega_1=r_{1,1}e_1-v_1 h1(u)=u−2∥ω1∥2(u⋅ω1)ω1ω1=r1,1e1−v1
如下图:
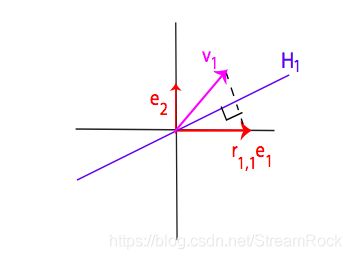
图3、 利用定理2,所得 v 1 v_1 v1 与 e 1 e_1 e1 之间的平面反射 H 1 H_1 H1
由上可知, r 1 r_1 r1 在由基矢量 e 1 e_1 e1 张成的子空间中,而且 r 1 , 1 = ∥ v 1 ∥ r_{1,1}=\Vert v_1 \Vert r1,1=∥v1∥ 为非负,满足所证定理。
接下来,我们假设已找到 k k k 个线性映射 h 1 , ⋯ , h k , 1 ≤ k ≤ n − 1 h_1,\cdots,h_k,\ 1\le k \le n-1 h1,⋯,hk, 1≤k≤n−1,它们若不是超平面反射(Hyperplane Reflection)便是全等映射(Identity),而且,在这些线性映射复合映射下有:
r j = h k ∘ h k − 1 ∘ ⋯ h 2 ∘ h 1 ( v j ) r_j = h_k\circ h_{k-1}\circ\cdots h_2 \circ h_1(v_j) rj=hk∘hk−1∘⋯h2∘h1(vj)
每个 r j r_j rj 皆可以表示为部分基 ( e 1 , ⋯ , e j ) , 1 ≤ j ≤ k (e_1,\cdots,e_j),\ 1\le j \le k (e1,⋯,ej), 1≤j≤k 的线性组合,如下图:

图4、 h 1 h_1 h1 的构建
由部分基 ( e 1 , ⋯ , e k ) (e_1,\cdots,e_k) (e1,⋯,ek) 可张成子空间 U k ′ U_k' Uk′,余下部分基 ( e k + 1 , ⋯ , e n ) (e_{k+1},\cdots,e_n) (ek+1,⋯,en) 可张成子空间 U k ′ ′ U_k'' Uk′′,则有
E = U k ′ ⊕ U k ′ ′ E=U_k'\oplus U_k'' E=Uk′⊕Uk′′
令
u k + 1 = h k ∘ h k − 1 ∘ ⋯ h 2 ∘ h 1 ( v k + 1 ) u_{k+1} = h_k\circ h_{k-1}\circ\cdots h_2 \circ h_1(v_{k+1}) uk+1=hk∘hk−1∘⋯h2∘h1(vk+1)
这条等式表示矢量 v k + 1 v_{k+1} vk+1 经过顺序的k次反射后得到的矢量,我们可以将它 u k + 1 u_{k+1} uk+1 表示为
u k + 1 = u k + 1 ′ + u k + 1 ′ ′ u_{k+1} = u_{k+1}'+u_{k+1}'' uk+1=uk+1′+uk+1′′
其中, u k + 1 ′ ∈ U k ′ , u k + 1 ′ ′ ∈ U k ′ ′ u_{k+1}'\in U_k',\ u_{k+1}''\in U_k'' uk+1′∈Uk′, uk+1′′∈Uk′′ ,以 h 1 ( v 2 ) h_1(v_2) h1(v2) 为例,如下图:
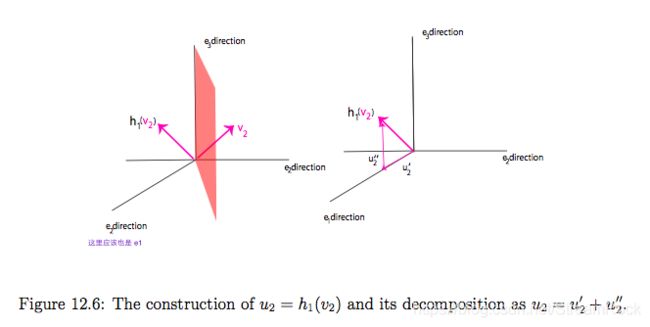
图5、矢量 v 2 v_2 v2 在由图4构建的 h 1 h_1 h1 的反射下获得的 h 1 ( v 2 ) h_1(v_2) h1(v2)
上面已经论述 h k h_k hk 满足了要求,接下来要构建 h k + 1 h_{k+1} hk+1。令
r k + 1 , k + 1 = ∥ u k + 1 ′ ′ ∥ r_{k+1,k+1}=\Vert u_{k+1}'' \Vert rk+1,k+1=∥uk+1′′∥
如果 u k + 1 ′ ′ = r k + 1 , k + 1 e k + 1 u_{k+1}''=r_{k+1,k+1}e_{k+1} uk+1′′=rk+1,k+1ek+1,我们可以令 h k + 1 = i d h_{k+1}=id hk+1=id,容易验证,这是符合定理要求的。否则,就存在唯一的超平面反射 h k + 1 h_{k+1} hk+1 使得:
h k + 1 ( u k + 1 ′ ′ ) = r k + 1 , k + 1 e k + 1 h_{k+1}(u_{k+1}'')=r_{k+1,k+1}e_{k+1} hk+1(uk+1′′)=rk+1,k+1ek+1
由此,我们得到超平面反射 h k + 1 h_{k+1} hk+1 的定义:
h k + 1 ( u ) = u − 2 u ⋅ ω k + 1 ∥ ω k + 1 ∥ 2 ω k + 1 h_{k+1}(u)=u-2\frac{u\cdot \omega_{k+1}}{\Vert \omega_{k+1}\Vert^2}\omega_{k+1} hk+1(u)=u−2∥ωk+1∥2u⋅ωk+1ωk+1
其中,超平面 H k + 1 H_{k+1} Hk+1 的法向量 ω k + 1 \omega_{k+1} ωk+1 是:
ω k + 1 = r k + 1 , k + 1 e k + 1 − u k + 1 ′ ′ \omega_{k+1} = r_{k+1,k+1}e_{k+1} - u_{k+1}'' ωk+1=rk+1,k+1ek+1−uk+1′′
由此定义得到的 h k + 1 h_{k+1} hk+1 就是关于超平面 H k + 1 H_{k+1} Hk+1 正交于 ω k + 1 \omega_{k+1} ωk+1 的超平面反射。
由前述,
u k + 1 = h k ∘ h k − 1 ∘ ⋯ h 2 ∘ h 1 ( v k + 1 ) u k + 1 = u k + 1 ′ + u k + 1 ′ ′ u_{k+1} = h_k\circ h_{k-1}\circ\cdots h_2 \circ h_1(v_{k+1}) \\ u_{k+1} = u_{k+1}'+u_{k+1}'' uk+1=hk∘hk−1∘⋯h2∘h1(vk+1)uk+1=uk+1′+uk+1′′
部分基 ( e 1 , ⋯ , e k ) (e_1,\cdots,e_k) (e1,⋯,ek) 张成子空间 U k ′ U_k' Uk′,余下部分基 ( e k + 1 , ⋯ , e n ) (e_{k+1},\cdots,e_n) (ek+1,⋯,en) 张成子空间 U k ′ ′ U_k'' Uk′′,且有 u k + 1 ′ ∈ U k ′ , u k + 1 ′ ′ ∈ U k ′ ′ u_{k+1}'\in U_k',\ u_{k+1}''\in U_k'' uk+1′∈Uk′, uk+1′′∈Uk′′ 。又因为, u k + 1 ′ ′ , e k + 1 ∈ U k ′ ′ u_{k+1}'',e_{k+1}\in U_k'' uk+1′′,ek+1∈Uk′′ 而 U k ′ ⊥ U k ′ ′ U_k' \bot U_k'' Uk′⊥Uk′′,所以,子空间 U k ′ ⊂ H k + 1 U_k' \subset H_{k+1} Uk′⊂Hk+1,因此, e 1 , ⋯ , e k , u k + 1 ′ ∈ H k + 1 e_1,\cdots,e_k,u_{k+1}'\in H_{k+1} e1,⋯,ek,uk+1′∈Hk+1,于是在关于 H k + 1 H_{k+1} Hk+1 的超平面反射下,这些矢量,以及由它们线性组合而成的线性矢量都保持不变,即:
x = λ 1 e 1 + ⋯ + λ k e k h k + 1 ( x ) = x h k + 1 ( u k + 1 ′ ) = u k + 1 ′ x=\lambda_1 e_1 +\cdots + \lambda_k e_k \\ h_{k+1}(x) = x \\ h_{k+1}(u_{k+1}')=u_{k+1}' x=λ1e1+⋯+λkekhk+1(x)=xhk+1(uk+1′)=uk+1′
由此,
h k + 1 ( u k + 1 ) = h k + 1 ( u k + 1 ′ ) + h k + 1 ( u k + 1 ′ ′ ) = u k + 1 ′ + r k + 1 , k + 1 e k + 1 h_{k+1}(u_{k+1})=h_{k+1}(u_{k+1}')+h_{k+1}(u_{k+1}'')=u_{k+1}'+r_{k+1,k+1}e_{k+1} hk+1(uk+1)=hk+1(uk+1′)+hk+1(uk+1′′)=uk+1′+rk+1,k+1ek+1
上式前一项可由 e 1 , ⋯ , e k e_1,\cdots,e_k e1,⋯,ek 线性组合而成,后一项是在 e k + 1 , k + 1 e_{k+1,k+1} ek+1,k+1 上,因此, h k + 1 , k + 1 ( u k + 1 ) h_{k+1,k+1}(u_{k+1}) hk+1,k+1(uk+1) 可以由部分基 ( e 1 , ⋯ , e k + 1 ) (e_1,\cdots,e_{k+1}) (e1,⋯,ek+1) 线性表示,令
r k + 1 = h k + 1 , k + 1 ( u k + 1 ) = h k + 1 ∘ ⋯ h 2 ∘ h 1 ( v k + 1 ) r_{k+1} = h_{k+1,k+1}(u_{k+1})=h_{k+1}\circ\cdots h_2 \circ h_1(v_{k+1}) rk+1=hk+1,k+1(uk+1)=hk+1∘⋯h2∘h1(vk+1)
r k + 1 r_{k+1} rk+1 可以由 e 1 , ⋯ , e k + 1 e_1,\cdots,e_{k+1} e1,⋯,ek+1 线性组合而成。另外,像 r k + 1 r_{k+1} rk+1 在 e k + 1 e_{k+1} ek+1 上的坐标为 r k + 1 , k + 1 = ∥ u k + 1 ′ ′ ∥ r_{k+1,k+1}=\Vert u_{k+1}''\Vert rk+1,k+1=∥uk+1′′∥,为非负。
综上,定理在 n = 1 n=1 n=1 时成立,而且当 n ≥ 1 n\ge 1 n≥1 成立时, n + 1 n+1 n+1 时也成立,根据递推法,此定理成立,证毕。
为了给出一个直观认识,以下是一个例子,如图:
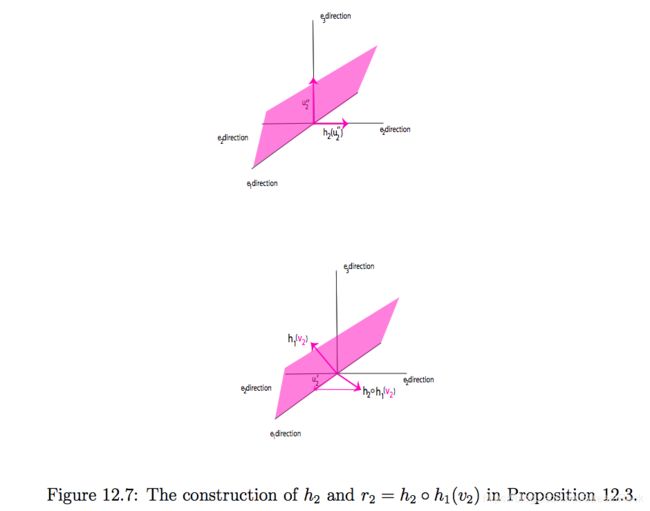
图6、 v 2 v_2 v2 经 h 1 h_1 h1 反射后得到 u 2 u_2 u2,它可以分解为 u 2 ′ , u 2 ′ ′ u_2',u_2'' u2′,u2′′, u 2 ′ u_2' u2′在接下来的反射 h 2 h_2 h2 下保持不变, u 2 ′ ′ u_2'' u2′′ 在 h 2 h_2 h2 作用下得到 h 2 ( u 2 ′ ′ ) = r 2 , 2 e 2 h_2(u_2'')=r_{2,2}e_2 h2(u2′′)=r2,2e2,最终 u 1 ′ + r 2 , 2 e 2 u_1'+r_{2,2}e_2 u1′+r2,2e2 得到 r 2 = h 2 ∘ h 1 ( v 2 ) r_2=h_2\circ h_1(v_2) r2=h2∘h1(v2)前面,已经完成了定理证明的大部分,还差最后一步了。
定理4:
对于任意 n × n n\times n n×n 实矩阵 A A A,存在一个矩阵序列 H 1 , ⋯ , H n H_1,\cdots,H_n H1,⋯,Hn,其中每个 H i H_i Hi 要不是 Householder Matrix,就是 Identity,使 R = H n ⋯ H 2 H 1 A R=H_n \cdots H_2 H_1 A R=Hn⋯H2H1A 是一个上三角矩阵。由此,存在一个正交矩阵 Q Q Q,使 A = Q R A=QR A=QR,即 A A A 的QR分解。更进一步,我们可以通过选择 Q Q Q 的列向量,使 R R R的对角元素为非负实数。
证明:
我们将矩阵 A A A 的各列看作定理3的矢量序列 ( v 1 , ⋯ , v n ) (v_1,\cdots,v_n) (v1,⋯,vn),基是 R n \mathbb R^n Rn标准基 ( e 1 , ⋯ , e n ) (e_1,\cdots,e_n) (e1,⋯,en)。应用定理3,我们得到一组映射 h 1 , ⋯ , h n h_1,\cdots,h_n h1,⋯,hn,其中, h j , 1 ≤ j ≤ n h_j,1\le j\le n hj,1≤j≤n 是一个 hyperplane reflection,或是一个 identity,则可得到:
r j = h n ∘ ⋯ ∘ h 2 ∘ h 1 ( v j ) r_j = h_n\circ \cdots \circ h_2 \circ h_1(v_j) rj=hn∘⋯∘h2∘h1(vj)
r j r_j rj 必是部分基 ( e 1 , ⋯ , e j ) , 1 ≤ j ≤ n (e_1,\cdots,e_j),1\le j \le n (e1,⋯,ej),1≤j≤n 的线性组合。令矩阵 R R R 的列向量是 r j r_j rj, H i H_i Hi 是 hyperplane reflection 或是 identity 映射对应的矩阵,有:
R = H n ⋯ H 2 H 1 A R=H_n\cdots H_2 H_1 A R=Hn⋯H2H1A
由上分析知, R R R 是上三角矩阵,而 H i H_i Hi 是 Householder Matrix 或 Identity Matrix。又因为 h i ∘ h i = i d , 1 ≤ i ≤ n h_i \circ h_i = id, 1\le i \le n hi∘hi=id,1≤i≤n,所以有
v j = h 1 ∘ h 2 ∘ ⋯ ∘ h n ( r j ) v_j = h_1\circ h_2 \circ \cdots \circ h_n(r_j) vj=h1∘h2∘⋯∘hn(rj)
由此,映射 ρ = h 1 ∘ h 2 ∘ ⋯ ∘ h n \rho = h_1\circ h_2 \circ \cdots \circ h_n ρ=h1∘h2∘⋯∘hn 是一个等距映射 isometry,可以用正交矩阵 Q = H 1 H 2 ⋯ H n Q=H_1H_2\cdots H_n Q=H1H2⋯Hn 表示。由此, A = Q R A=QR A=QR,其中 Q Q Q是正交矩阵,而 R R R 是上三角矩阵,其对角元素可以通过Q的列向量选择保持非负。证毕。
至此,通过上述定理的证明,我们已证明了QR的存在性,以及如何进行QR分解的方法,下面我们将看到如何利用这里的定理获得QR分解的代码实现。
四、QR分解的代码实现
《矩阵论简明教程》p104
在【1】中给出了详细的基于 Householder Reflection 方法的 QR分解MATLAB 实现代码,我这里仅挑选了部分,用 python 将它翻译了一次,若要看看详细代码,可以在【1】的 p417 找到。
该方法应用 Householder reflections 方法,为得到 R R R 并不直接求Householder 矩阵的乘积,具有很好的数值稳定性和效率。
import numpy as np
def signe(x):
# if x >= 0, then signe(x)=1
# else if x < 0, then signe(x)=-1
if x<0:
s = -1
else:
s = 1
return s
def house(x):
# This constructs the unnormalized vector uu
# defining the Householder reflection that
# zeros all but the first entries in x.
# u is the normalized vector uu/||uu||
tol = 2*10**(-15) # tolerance
uu = x.copy()
p = np.shape(x)[0]
# computes l^1-norm of x[1:]
n1 = np.sum(np.abs(x[1:]))
if n1 <= tol:
u = np.zeros((p,1),dtype=np.float32)
uu = u
else:
l = np.sqrt(np.matmul(x.transpose(),x)) # l^2 norm of x
uu[0] = x[0] + signe(x[0])*l
u = uu/np.sqrt(np.matmul(uu.transpose(),uu))
return uu,u
def houseeqr(A):
# This function computes the upper triangular
# R in QR factorization of A using Householder
# reflections, and an implicit representation
# of Q as sequence of n-1 vectors u_i representing
# Householder reflections
n = np.shape(A)[0]
R = A
u = np.zeros([n, n],dtype=np.float32)
for i in range(n-1):
x = R[i:,i]
x = x.reshape([len(x),1])
_, uu = house(x)
u[i:,i:i+1] = uu
if any(uu == np.zeros_like(uu)):
R[i:, i] = np.zeros_like(R[i:, i])
else:
R[i:,i:] = R[i:,i:] - 2*np.matmul(np.matmul(uu,uu.transpose()),R[i:,i:])
return R,u
A = np.asarray([[1.0, 2.0, 3.0, 4.0],[2.0, 3.0, 4.0, 5.0],[3.0, 4.0, 5.0, 6.0],[4.0, 5.0, 6.0, 7.0]])
R, u = houseeqr(A)
for i in range(4):
for j in range(4):
if abs(R[i,j]) < 0.001:
R[i,j] = 0
print(R)
>[[ -5.47722558 -7.30296743 -9.12870929 -10.95445115]
[ 0. -0.81649658 -1.63299316 -2.44948974]
[ 0. 0. 0. 0. ]
[ 0. 0. 0. 0. ]]
以上代码,函数 house( ) 的目的是求反射平面法矢量。为了使 ∥ P x ∥ \Vert Px \Vert ∥Px∥ 尽可能大,在计算法矢量 uu(u 是它的归一化)时,我们没有选择原公式
u u = x − ∥ x ∥ e 1 uu=x-\Vert x \Vert e_1 uu=x−∥x∥e1
而是选择了:
u u = x + s i g n ( x 1 ) ∥ x ∥ e 1 uu=x + sign(x_1)\Vert x \Vert e_1 uu=x+sign(x1)∥x∥e1
其结果是一样的,因为符号不影响所确定的反射平面。
函数 houseeqr( ) 求得上三角矩阵,不需显示计算 Householder 矩阵乘。这个处理方法也可以在【3】中 定理4.8 和 定理4.5 处找到证明过程。此处,就不再赘述了。
小结
QR 分解有着非常明确的几何意义,采用超平面反射的方法不仅可以揭示其几何关系,而且为我们提供了一种求解 QR 分解的方法。最后,《Algebra, Topology, Differential, Calculus, and Optimization Theory》是一本不可多得的好书,不仅内容覆盖面广、推导详细,而且通俗易懂,与实现代码结合紧密,是从普通大学数学进阶到算法研究的极好学习材料,值得好好学习。若有一起学习的同学,不妨结伴同行。
参考文献
【1】http://www.cis.upenn.edu/~jean/math-basics.pdf
【2】https://www.cis.upenn.edu/~jean/home.html
【3】《矩阵论简明教程》,徐仲、张凯院等,科学出版社,2001.
【4】《Matrix Analysis 矩阵分析》Roger A.Horn(美),杨奇(译) 机械工业出版社,2004