本文首发自:稀土掘金、思否
博客代码已上传至github
点击这里 即可访问
另提供:完整代码(ts+rollup)和视频教程
序
所谓算法指的是:把一种数据结构转化为另外一种数据结构的方法。
在runtime(运行时)阶段存在一个无论如何都绕不过去的核心功能,那就是diff 算法。
本博客将基于最新(2023年1月20日)的vue 3.2 版本,为大家详细讲解diff 算法逻辑,博客内容较长(已经尽量精简)、并且有点难,所以请预留足够的时间来进行阅读。
本博客讲解diff 算法的方式,将按照如下顺序进行:
- diff 算法的触发场景
- v-for 循环时,key 属性的意义
- diff 算法的5 大步
- diff 算法的前四步详解
- 最长递增子序列
- diff 算法的第五步详解
明确好步骤之后,那么下面就让咱们进入到diff 算法的逻辑分析之中吧!
diff 算法的触发场景
想要搞明白diff 算法的处理逻辑,那么首先咱们需要先搞清楚 diff 究竟在什么时候会被触发。
这里存在一个 误区,因为有很多小伙伴会认为:只要触发了 dom 的更新,那么就会使用 diff。这是不对的!
diff 算法 本质上是一个 对比的方法。其核心就是在:“旧 DOM 组”更新为“新 DOM 组”时,如何更新才能效率更高。
注意: 这里我们说的是 “旧 DOM 组” 和 “新 DOM 组”。也就是说:想要触发diff,那么一定是一组 dom发生的变化。
那么什么时候会触发一组 dom 的变化呢?
这在咱们日常开发中是非常常见的。比如我们来看如下代码(vue 3.2 版本,基于 Options API 编写 ):
-
item: {{ item.title }} - key: {{ item.id }}
在上面的代码中:
- 首先:创建了一个数组
arr,值为a、b、c - 其次:通过
v-for循环,对arr进行了渲染,并且以id为key - 最后:当点击按钮时,修改
arr[2]的数据,把c变为d
当触发点击行为时,arr 数组发生变化,此时旧的一组 li 会被变为新的一组 li,那么此时就是一组 dom发生的变化,也就会触发diff。
阶段一总结
那么下面咱们对diff 算法的触发场景进行下总结。
diff 算法会在:一组 dom 更新时被触发,比如:通过 v-for 循环的 li 标签。
PS:大家可以通过这个仓库 下的测试实例通过debugger的形式进行验证diff被触发。
v-for 循环时,key 属性的意义
咱们知道,当使用v-for进行dom循环渲染时需要指定key属性。这个key属性在diff时也起到了非常重要的作用,所以咱们单独把它拿出来说。
如果大家仔细观察上面案例点击按钮时dom的更新情况,其实大家可以发现:上面的更新中,只有第三个 li 标签进行了重新渲染,其他的两个 li 标签是没有变化的。
有些小伙伴看到这里可能会说:这不很正常吗?因为只有第三个 dom 发生了变化啊。所以只需要让第三个 dom 重新渲染就可以了,前两个不需要变化。
但是大家要注意,上面的结论是咱们从开发者的角度看出来的。那么 程序是如何判断出前两个 dom 没有变化的呢?
想要知道这个,那么咱们就需要来看下 vue 源码的 isSameVNodeType 方法。
该方法在源码中可能比较复杂,咱们可以对它进行适当的简化,以方便大家进行观察:
/**
* 根据 key || type 判断是否为相同类型节点
*/
export function isSameVNodeType(n1: VNode, n2: VNode): boolean {
return n1.type === n2.type && n1.key === n2.key
}根据上面简化之后的代码,咱们可以看出:
isSameVNodeType的作用是:判断两个vnode是否为相同的- 判断的方式是:利用
vnode的type和key进行对比,如果两个vnode的type、key相等,则两个 vnode 为相同的 vnode
那么这里的type 和key分别代表是什么意思呢?
type
首先咱们来说type。 这里的type表示:VNode 的节点类型。 比如:
- 一个
div节点,vnode就是div - 一个
li节点,vnode就是li - 一个
注释节点,vnode就是comment - 一个
组件节点,vnode就是Component 对象实例 - ......
如果我们以上面的v-for 循环案例为例,则li标签的type === 'li'
key
这里key相信大家肯定已经有了自己的猜测吧。
这个key就是v-for 循环时,绑定的 key 值。
根据上面的v-for 循环案例,咱们可以看到:当触发按钮事件时,arr[2]的 id 是发生了变化的。所以它的key 也必然发生了变化。
我们可以通过以下两个vnode来表示这样的变化:
- 变化前的
vnode:
const arr0VNode = h('li', {
key: 1
}, 'a')
const arr1VNode = h('li', {
key: 2
}, 'b')
const arr2VNode = h('li', {
key: 3
}, 'c')- 变化后的
vnode:
const arr0VNode = h('li', {
key: 1
}, 'a')
const arr1VNode = h('li', {
key: 2
}, 'b')
const arr2VNode = h('li', {
key: 4
}, 'd')也就是说,如果通过isSameVNodeType方法判断则:
arr[0] vnode 对比:true(两个 vnode 是相同的)arr[1] vnode 对比:true(两个 vnode 是相同的)arr[2] vnode 对比:false(两个 vnode 不同,需要更新)
阶段二总结
根据上面的内容咱们可以知道:
- vue 通过
isSameVNodeType判断两个“节点”是否相同 isSameVNodeType主要依赖type和key进行判断type表示节点的类型key表示节点的唯一标识isSameVNodeType返回为true则不需要更新,返回为false则需要更新
diff 算法的5 大步
那么此时咱们已经知道diff会在什么情况下被触发了,那么接下来咱们看下diff的大致执行步骤。
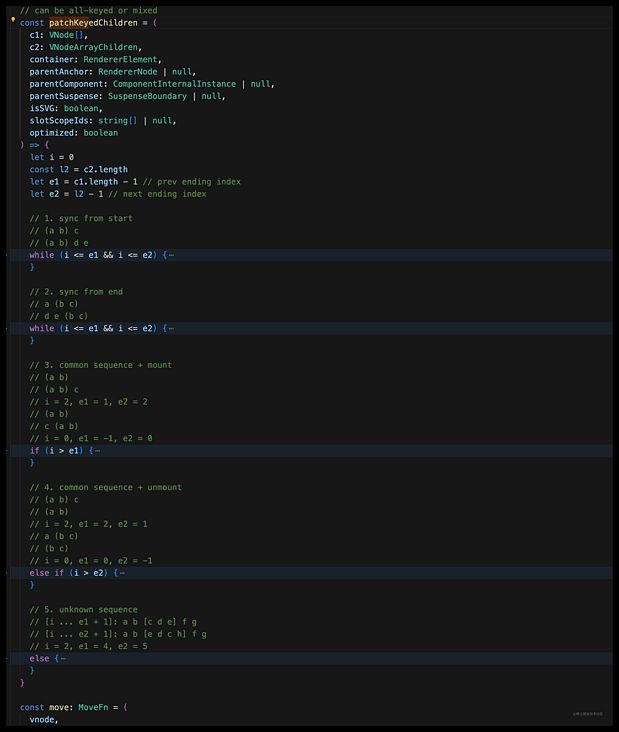
其实根据标题咱们也知道,diff 的整体执行步骤被分为 5 步,咱们可以通过源码 来看到详细的步骤分布(下面为折叠代码之后的截图):
阶段三总结
从上面的截图中,可以很清楚的看到整个diff的分步共分为 5 步,分别为:
sync from start:自前向后的对比sync from end:自后向前的对比common sequence + mount:新节点多于旧节点,需要挂载common sequence + unmount:旧节点多于新节点,需要卸载unknown sequence:乱序
这5步的对比决定了一组DOM更新时的最优方案。
# diff 算法的前四步详解
根据上面的内容咱们知道,整个diff被分为了5步。那么这 5 步,其实可以被分为两大块来看:
- 第一大块:前四步
- 第二大块:第五步
所以,咱们在后面的讲解中,把前四步综合到一起去讲,把第五步单独来讲。
第一步:sync from start 自前向后的对比
谨记: diff 场景一定是两组 dom 的对比
diff 的第一步主要是进行:两组 dom 的自前向后对比。 其核心的目的是:把两组 dom 自前开始,相同的 dom 节点(vnode)完成对比处理
下面我们把源码添加了详细备注(进行了适当简化):
const patchKeyedChildren = (
oldChildren,
newChildren,
container,
parentAnchor
) => {
/**
* 索引
*/
let i = 0
/**
* 新的子节点的长度
*/
const newChildrenLength = newChildren.length
/**
* 旧的子节点最大(最后一个)下标
*/
let oldChildrenEnd = oldChildren.length - 1
/**
* 新的子节点最大(最后一个)下标
*/
let newChildrenEnd = newChildrenLength - 1
// 1. 自前向后的 diff 对比。经过该循环之后,从前开始的相同 vnode 将被处理
while (i <= oldChildrenEnd && i <= newChildrenEnd) {
const oldVNode = oldChildren[i]
const newVNode = normalizeVNode(newChildren[i])
// 如果 oldVNode 和 newVNode 被认为是同一个 vnode,则直接 patch 即可
if (isSameVNodeType(oldVNode, newVNode)) {
patch(oldVNode, newVNode, container, null)
}
// 如果不被认为是同一个 vnode,则直接跳出循环
else {
break
}
// 下标自增
i++
}在上面的代码中,主要进行了两大步的处理逻辑:
自前向后的 diff 比对中,会 依次获取相同下标的
oldChild和newChild:- 如果
oldChild和newChild为 相同的VNode,则直接通过patch进行打补丁即可 - 如果
oldChild和newChild为 不相同的VNode,则会跳出循环
- 如果
- 每次处理成功,则会自增
i标记,表示:自前向后已处理过的节点数量
通过第一步,我们可以处理:从前开始,相同的 vnode。 直到遇到不同的 vnode 为止。
第二步:sync from end:自后向前的对比
如果大家可以理解第一步的逻辑处理,那么针对于第二步就很会很好理解了。
第二步的逻辑与第一步 反过来 。即:两组 dom 的自后向前对比。 其核心的目的是:把两组 dom 自后开始,相同的 dom 节点(vnode)完成对比处理
同样,咱们把源码添加了详细备注(进行了适当简化):
// 2. 自后向前的 diff 对比。经过该循环之后,从后开始的相同 vnode 将被处理
while (i <= oldChildrenEnd && i <= newChildrenEnd) {
const oldVNode = oldChildren[oldChildrenEnd]
const newVNode = normalizeVNode(newChildren[newChildrenEnd])
if (isSameVNodeType(oldVNode, newVNode)) {
patch(oldVNode, newVNode, container, null)
} else {
break
}
// 最后的下标递减
oldChildrenEnd--
newChildrenEnd--
}在上面的代码中,大家可以发现整体的代码逻辑与第一步其实是非常类似的。
唯一不同的是:每次处理成功之后,会自减 oldChildrenEnd 和 newChildrenEnd ,表示:新、旧节点中已经处理完成节点(自后向前)
第三步:common sequence + mount:新节点多于旧节点,需要挂载
第一步和第二步的处理,都有一个前提条件,那就是:新节点数量和旧节点数量是完全一致的。
但是在日常开发中,咱们经常也会遇到新旧节点数量不一致的情况。具体可以分为两种:
- 新节点的数量多于旧节点的数量(如:
arr.push(item)) - 旧节点的数量多于新节点的数量(如:
arr.pop(item))
那么第三步和第四步就是用来处理这两种情况的。
那么这里咱们先来看新节点多于旧节点这种情况。
咱们想要让 “新节点多于旧节点”,那么咱们其实有两种方式:
- 执行
arr.push():这样可以把新数据添加到尾部。即:多出的新节点位于 尾部 - 执行
arr.unshift():这样可以把新数据添加到头部。即:多出的新节点位于 头部
那么明确好以上内容之后,下面咱们来看下第三步代码:
// 3. 新节点多余旧节点时的 diff 比对。
if (i > oldChildrenEnd) {
if (i <= newChildrenEnd) {
const nextPos = newChildrenEnd + 1
// 重点:找到锚点
const anchor =
nextPos < newChildrenLength ? newChildren[nextPos].el : parentAnchor
while (i <= newChildrenEnd) {
patch(null, normalizeVNode(newChildren[i]), container, anchor)
i++
}
}
}由上面的代码可知:
对于 新节点多于旧节点 的场景具体可以再细分为两种情况:
- 多出的新节点位于 尾部
- 多出的新节点位于 头部
- 这两种情况下的区别在于:插入的位置不同
- 明确好插入的位置之后,直接通过
patch进行打补丁即可。
第四步:common sequence + unmount:旧节点多于新节点,需要卸载
接下来我们来看第四步 旧节点多于新节点时
根据第三步的经验,其实我们也可以明确,对于旧节点多于新节点时,对应的场景也可以细分为两种:
- 执行
arr.pop():这样可以从 尾部 删除数据。即:多出的旧节点位于 尾部 - 执行
arr.shift():这样可以从 头部 删除数据。即:多出的旧节点位于 头部
同时第四步的代码会比第三步更加简单一些,咱们来看对应的代码:
// 4. 旧节点多与新节点时的 diff 比对。
else if (i > newChildrenEnd) {
while (i <= oldChildrenEnd) {
// 卸载 dom
unmount(oldChildren[i])
i++
}
}由以上代码可知:
- 旧节点多于新节点时,整体的处理比较简单,只需要 卸载旧节点即可
阶段四总结
在阶段四中,咱们了解了整个diff 前四步的逻辑。通过前四步,咱们可以处理如下 4 中场景:
- 自前向后的 diff 对比
- 自后向前的 diff 对比
- 新节点多于旧节点时的 diff 比对
- 旧节点多于新节点时的 diff 比对
但是以上的四种场景都是比较特殊的场景,所以咱们还需要有最重要的第五步-乱序。
针对于第五步,是整个diff中最复杂的一块逻辑,想要学习它,咱们还需要提前掌握一个东西,那就是最长递增子序列
最长递增子序列
在第五步的 diff 中,vue 使用了 最长递增子序列 这样的一个概念,所以想要更好地理解第五步,那么我们需要先搞明白两个问题:
- 什么是最长递增子序列?
- 最长递增子序列在
diff中的作用是什么?
什么是最长递增子序列
在一个给定的数值序列中,找到一个子序列,使得这个子序列元素的数值依次递增,并且这个子序列的长度尽可能地大。
只看概念可能难以理解,我们来看一个具体的例子。
假设,我们现在有一个这样两组节点:
旧节点:1,2,3,4,5,6
新节点:1,3,2,4,6,5我们可以根据 新节点 生成 递增子序列(非最长)(注意:并不是惟一的) ,其结果为:
1、3、61、2、4、6- ...
最长递增子序列在 diff 中的作用是什么
那么现在我们成功得到了递增子序列,那么下面我们来看,这两个递增子序列在我们接下来的 diff 中起到了什么作用。
根据我们之前的四种场景可知,所谓的 diff,其实说白了就是对 一组节点 进行 添加、删除、打补丁 的对应操作。那么除了以上三种操作之外,其实还有最后一种操作方式,那就是 移动。
对于以上的节点对比而言,如果我们想要把 旧节点转化为新节点,那么将要涉及到节点的 移动,所以问题的重点是:如何进行移动。
那么接下来,我们来分析一下移动的策略,整个移动根据递增子序列的不同,将拥有两种移动策略:
1、3、6递增序列下:- 因为
1、3、6的递增已确认,所以它们三个是不需要移动的,那么我们所需要移动的节点无非就是 三 个2、4、5。 - 所以我们需要经过 三次 移动
- 因为
1、2、4、6递增序列下:- 因为
1、2、4、6的递增已确认,所以它们四个是不需要移动的,那么我们所需要移动的节点无非就是 两个3、5。 - 所以我们需要经过 两次 移动
- 因为
所以由以上分析,我们可知:最长递增子序列的确定,可以帮助我们减少移动的次数
所以,当我们需要进行节点移动时,移动需要事先构建出最长递增子序列,以保证我们的移动方案。
点击这里可以查看 vue 中求解最长递增子序列的代码,通过源码可以发现:vue 通过 getSequence 函数处理的最长递增子序列
该函数算法来自于 维基百科(贪心 + 二分查找),我们复制了 vue 3 中 getSequence 的所有代码,并为其加入了 详细的备注,如下:
/**
* 获取最长递增子序列下标
* 维基百科:https://en.wikipedia.org/wiki/Longest_increasing_subsequence
* 百度百科:https://baike.baidu.com/item/%E6%9C%80%E9%95%BF%E9%80%92%E5%A2%9E%E5%AD%90%E5%BA%8F%E5%88%97/22828111
*/
function getSequence(arr) {
// 获取一个数组浅拷贝。注意 p 的元素改变并不会影响 arr
// p 是一个最终的回溯数组,它会在最终的 result 回溯中被使用
// 它会在每次 result 发生变化时,记录 result 更新前最后一个索引的值
const p = arr.slice()
// 定义返回值(最长递增子序列下标),因为下标从 0 开始,所以它的初始值为 0
const result = [0]
let i, j, u, v, c
// 当前数组的长度
const len = arr.length
// 对数组中所有的元素进行 for 循环处理,i = 下标
for (i = 0; i < len; i++) {
// 根据下标获取当前对应元素
const arrI = arr[i]
//
if (arrI !== 0) {
// 获取 result 中的最后一个元素,即:当前 result 中保存的最大值的下标
j = result[result.length - 1]
// arr[j] = 当前 result 中所保存的最大值
// arrI = 当前值
// 如果 arr[j] < arrI 。那么就证明,当前存在更大的序列,那么该下标就需要被放入到 result 的最后位置
if (arr[j] < arrI) {
p[i] = j
// 把当前的下标 i 放入到 result 的最后位置
result.push(i)
continue
}
// 不满足 arr[j] < arrI 的条件,就证明目前 result 中的最后位置保存着更大的数值的下标。
// 但是这个下标并不一定是一个递增的序列,比如: [1, 3] 和 [1, 2]
// 所以我们还需要确定当前的序列是递增的。
// 计算方式就是通过:二分查找来进行的
// 初始下标
u = 0
// 最终下标
v = result.length - 1
// 只有初始下标 < 最终下标时才需要计算
while (u < v) {
// (u + v) 转化为 32 位 2 进制,右移 1 位 === 取中间位置(向下取整)例如:8 >> 1 = 4; 9 >> 1 = 4; 5 >> 1 = 2
// https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Operators/Right_shift
// c 表示中间位。即:初始下标 + 最终下标 / 2 (向下取整)
c = (u + v) >> 1
// 从 result 中根据 c(中间位),取出中间位的下标。
// 然后利用中间位的下标,从 arr 中取出对应的值。
// 即:arr[result[c]] = result 中间位的值
// 如果:result 中间位的值 < arrI,则 u(初始下标)= 中间位 + 1。即:从中间向右移动一位,作为初始下标。 (下次直接从中间开始,往后计算即可)
if (arr[result[c]] < arrI) {
u = c + 1
} else {
// 否则,则 v(最终下标) = 中间位。即:下次直接从 0 开始,计算到中间位置 即可。
v = c
}
}
// 最终,经过 while 的二分运算可以计算出:目标下标位 u
// 利用 u 从 result 中获取下标,然后拿到 arr 中对应的值:arr[result[u]]
// 如果:arr[result[u]] > arrI 的,则证明当前 result 中存在的下标 《不是》 递增序列,则需要进行替换
if (arrI < arr[result[u]]) {
if (u > 0) {
p[i] = result[u - 1]
}
// 进行替换,替换为递增序列
result[u] = i
}
}
}
// 重新定义 u。此时:u = result 的长度
u = result.length
// 重新定义 v。此时 v = result 的最后一个元素
v = result[u - 1]
// 自后向前处理 result,利用 p 中所保存的索引值,进行最后的一次回溯
while (u-- > 0) {
result[u] = v
v = p[v]
}
return result
}我们可以通过以上代码,对 getSequence([1, 3, 2, 4, 6, 5]) 进行测试,debugger 代码的执行逻辑,从而明确当前算法的逻辑(博客中无法进行 debugger 演示 )。
阶段五总结
在这里咱们主要了解了最长递增子序列的概念,大家需要明确的是:最长递增子序列可以帮助咱们减少移动的次数,从而提升性能。
diff 算法的第五步详解
那么到目前为止,我们已经明确了:
diff指的就是:添加、删除、打补丁、移动 这四个行为- 最长递增子序列 是什么,如何计算的,以及在
diff中的作用 - 场景五的乱序,是最复杂的场景,将会涉及到 添加、删除、打补丁、移动 这些所有场景。
那么明确好了以上内容之后,接下来咱们就来看第五步的详细逻辑,同样添加了详细备注:
// 5. unknown sequence
// [i ... e1 + 1]: a b [c d e] f g
// [i ... e2 + 1]: a b [e d c h] f g
// i = 2, e1 = 4, e2 = 5
else {
// 旧子节点的开始索引:oldChildrenStart
const s1 = i
// 新子节点的开始索引:newChildrenStart
const s2 = i
// 5.1 创建一个 的 Map 对象 keyToNewIndexMap。通过该对象可知:新的 child(根据 key 判断指定 child) 更新后的位置(根据对应的 index 判断)在哪里
const keyToNewIndexMap: Map = new Map()
// 通过循环为 keyToNewIndexMap 填充值(s2 = newChildrenStart; e2 = newChildrenEnd)
for (i = s2; i <= e2; i++) {
// 从 newChildren 中根据开始索引获取每一个 child(c2 = newChildren)
const nextChild = (c2[i] = optimized
? cloneIfMounted(c2[i] as VNode)
: normalizeVNode(c2[i]))
// child 必须存在 key(这也是为什么 v-for 必须要有 key 的原因)
if (nextChild.key != null) {
// key 不可以重复,否则你将会得到一个错误
if (__DEV__ && keyToNewIndexMap.has(nextChild.key)) {
warn(
`Duplicate keys found during update:`,
JSON.stringify(nextChild.key),
`Make sure keys are unique.`
)
}
// 把 key 和 对应的索引,放到 keyToNewIndexMap 对象中
keyToNewIndexMap.set(nextChild.key, i)
}
}
// 5.2 循环 oldChildren ,并尝试进行 patch(打补丁)或 unmount(删除)旧节点
let j
// 记录已经修复的新节点数量
let patched = 0
// 新节点待修补的数量 = newChildrenEnd - newChildrenStart + 1
const toBePatched = e2 - s2 + 1
// 标记位:节点是否需要移动
let moved = false
// 配合 moved 进行使用,它始终保存当前最大的 index 值
let maxNewIndexSoFar = 0
// 创建一个 Array 的对象,用来确定最长递增子序列。它的下标表示:《新节点的下标(newIndex),不计算已处理的节点。即:n-c 被认为是 0》,元素表示:《对应旧节点的下标(oldIndex),永远 +1》
// 但是,需要特别注意的是:oldIndex 的值应该永远 +1 ( 因为 0 代表了特殊含义,他表示《新节点没有找到对应的旧节点,此时需要新增新节点》)。即:旧节点下标为 0, 但是记录时会被记录为 1
const newIndexToOldIndexMap = new Array(toBePatched)
// 遍历 toBePatched ,为 newIndexToOldIndexMap 进行初始化,初始化时,所有的元素为 0
for (i = 0; i < toBePatched; i++) newIndexToOldIndexMap[i] = 0
// 遍历 oldChildren(s1 = oldChildrenStart; e1 = oldChildrenEnd),获取旧节点(c1 = oldChildren),如果当前 已经处理的节点数量 > 待处理的节点数量,那么就证明:《所有的节点都已经更新完成,剩余的旧节点全部删除即可》
for (i = s1; i <= e1; i++) {
// 获取旧节点(c1 = oldChildren)
const prevChild = c1[i]
// 如果当前 已经处理的节点数量 > 待处理的节点数量,那么就证明:《所有的节点都已经更新完成,剩余的旧节点全部删除即可》
if (patched >= toBePatched) {
// 所有的节点都已经更新完成,剩余的旧节点全部删除即可
unmount(prevChild, parentComponent, parentSuspense, true)
continue
}
// 新节点需要存在的位置,需要根据旧节点来进行寻找(包含已处理的节点。即:n-c 被认为是 1)
let newIndex
// 旧节点的 key 存在时
if (prevChild.key != null) {
// 根据旧节点的 key,从 keyToNewIndexMap 中可以获取到新节点对应的位置
newIndex = keyToNewIndexMap.get(prevChild.key)
} else {
// 旧节点的 key 不存在(无 key 节点)
// 那么我们就遍历所有的新节点(s2 = newChildrenStart; e2 = newChildrenEnd),找到《没有找到对应旧节点的新节点,并且该新节点可以和旧节点匹配》(s2 = newChildrenStart; c2 = newChildren),如果能找到,那么 newIndex = 该新节点索引
for (j = s2; j <= e2; j++) {
// 找到《没有找到对应旧节点的新节点,并且该新节点可以和旧节点匹配》(s2 = newChildrenStart; c2 = newChildren)
if (
newIndexToOldIndexMap[j - s2] === 0 &&
isSameVNodeType(prevChild, c2[j] as VNode)
) {
// 如果能找到,那么 newIndex = 该新节点索引
newIndex = j
break
}
}
}
// 最终没有找到新节点的索引,则证明:当前旧节点没有对应的新节点
if (newIndex === undefined) {
// 此时,直接删除即可
unmount(prevChild, parentComponent, parentSuspense, true)
}
// 没有进入 if,则表示:当前旧节点找到了对应的新节点,那么接下来就是要判断对于该新节点而言,是要 patch(打补丁)还是 move(移动)
else {
// 为 newIndexToOldIndexMap 填充值:下标表示:《新节点的下标(newIndex),不计算已处理的节点。即:n-c 被认为是 0》,元素表示:《对应旧节点的下标(oldIndex),永远 +1》
// 因为 newIndex 包含已处理的节点,所以需要减去 s2(s2 = newChildrenStart)表示:不计算已处理的节点
newIndexToOldIndexMap[newIndex - s2] = i + 1
// maxNewIndexSoFar 会存储当前最大的 newIndex,它应该是一个递增的,如果没有递增,则证明有节点需要移动
if (newIndex >= maxNewIndexSoFar) {
// 持续递增
maxNewIndexSoFar = newIndex
} else {
// 没有递增,则需要移动,moved = true
moved = true
}
// 打补丁
patch(
prevChild,
c2[newIndex] as VNode,
container,
null,
parentComponent,
parentSuspense,
isSVG,
slotScopeIds,
optimized
)
// 自增已处理的节点数量
patched++
}
}
// 5.3 针对移动和挂载的处理
// 仅当节点需要移动的时候,我们才需要生成最长递增子序列,否则只需要有一个空数组即可
const increasingNewIndexSequence = moved
? getSequence(newIndexToOldIndexMap)
: EMPTY_ARR
// j >= 0 表示:初始值为 最长递增子序列的最后下标
// j < 0 表示:《不存在》最长递增子序列。
j = increasingNewIndexSequence.length - 1
// 倒序循环,以便我们可以使用最后修补的节点作为锚点
for (i = toBePatched - 1; i >= 0; i--) {
// nextIndex(需要更新的新节点下标) = newChildrenStart + i
const nextIndex = s2 + i
// 根据 nextIndex 拿到要处理的 新节点
const nextChild = c2[nextIndex] as VNode
// 获取锚点(是否超过了最长长度)
const anchor =
nextIndex + 1 < l2 ? (c2[nextIndex + 1] as VNode).el : parentAnchor
// 如果 newIndexToOldIndexMap 中保存的 value = 0,则表示:新节点没有用对应的旧节点,此时需要挂载新节点
if (newIndexToOldIndexMap[i] === 0) {
// 挂载新节点
patch(
null,
nextChild,
container,
anchor,
parentComponent,
parentSuspense,
isSVG,
slotScopeIds,
optimized
)
}
// moved 为 true,表示需要移动
else if (moved) {
// j < 0 表示:不存在 最长递增子序列
// i !== increasingNewIndexSequence[j] 表示:当前节点不在最后位置
// 那么此时就需要 move (移动)
if (j < 0 || i !== increasingNewIndexSequence[j]) {
move(nextChild, container, anchor, MoveType.REORDER)
} else {
// j 随着循环递减
j--
}
}
}
} 由以上代码可知:
- 乱序下的
diff是 最复杂 的一块场景 它的主要逻辑分为三大步:
- 创建一个
Map对象keyToNewIndexMap。通过该对象可知:新的child(根据key判断指定child) 更新后的位置(根据对应的index判断)在哪里
- 循环
oldChildren,并尝试进行patch(打补丁)或unmount(删除)旧节点 - 处理 移动和挂载
- 创建一个
总结
这应该是我写过最长的一篇纯技术干货的博客啦,总共花了两天的时间。在已经进行了精简的情况下,总字数依然超过了7000字。
希望这篇博客,可以帮助大家了解,甚至掌握diff的算法逻辑,以帮助大家在以后的面试、工作中获得提升。
那么,下次再见!