【精品课设】经典PID与模糊PID控制的对比与分析(一)
【精品课设】经典PID与模糊PID控制的对比与分析(一)
目录
- 【精品课设】经典PID与模糊PID控制的对比与分析(一)
-
- 0研究背景
- 1经典PID控制的设计
-
- 1.1 经典PID控制律的设计
- 1.2 被控对象传递函数的代码实现
- 1.3 基于频域PID参数的Z-N整定
- 2模糊PID控制的设计
-
- 2.1 模糊PID控制律的设计
- 2.2 模糊PID控制的仿真结果
- 3仿真对比与分析
0研究背景
写在前面:
1.本代码基于MATLAB2019a版本,低版本或者不同版本可能会报错,mdl文件或slx文件打开可能会失败;
2.如果运行时间过长,请观察设置参数是否一致。
3.本博客附上算法运行图并详细介绍,如果转载请注明出处;
4.如果本博客恰巧与您的研究有所关联,欢迎您的咨询qq1366196286 ,同时代码下载见评论的下载链接。
| 文档下载:https://download.csdn.net/download/qq_42249050/19746440 |
| 代码下载:https://download.csdn.net/download/qq_42249050/19746530 |
1经典PID控制的设计
1.1 经典PID控制律的设计
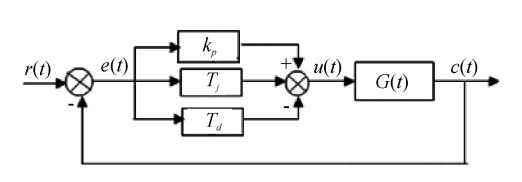
PID控制律的微分方程、各个环节的影响作用、以及Simulink组成在其他博客均有论述。如读者还存在疑惑,可转到之前的博客进行观看。
基于遗传算法的PID参数整定研究(一)
参数智能整定#基于智能算法的PID参数整定研究
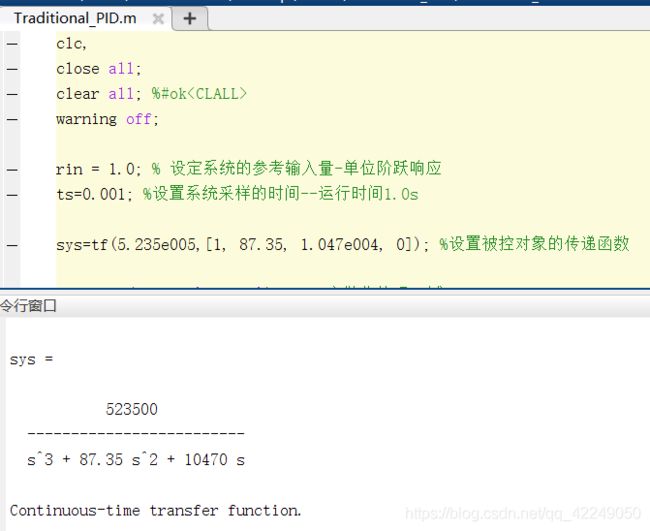
1.2 被控对象传递函数的代码实现
被控对象的传递函数为:
Continuous_PID.m
clc;
clear;
% Target = 1000; %目标值
% sys1= tf([0,300,200,350],[1,0.5,0.05,0]); %建立被控对象传递函数 零点为-1 极点为-50
%sys2=tf([0.02 1],1); %建立被控对象传递函数 无零点 极点为-20
%% 设置被控对象的传递函数
Target = 1.000;
sys1=tf(5.235e005,[1, 87.35, 1.047e004, 0]);
%% PID传递函数
% kp0=0.90; % PID控制参数的大小
% ki0=0.05;
% kd0=0.2;
Kp = 0.90;
Ki = 0.05;
Kd = 0;
sysP = Kp;
sysI = tf(Ki,[1,0]);
sysD = tf([Kd,0],1);
sysPI = parallel(sysP,sysI); %将比例积分微分环节并联得到PID传递函数
sysPID = parallel(sysPI,sysD);
sysG = series(sysPID,sys1); %将两传递函数串联 得到最终的传递函数G
sysH = 1; %反馈函数为空
sysResult = feedback(sysG,sysH); %负反馈
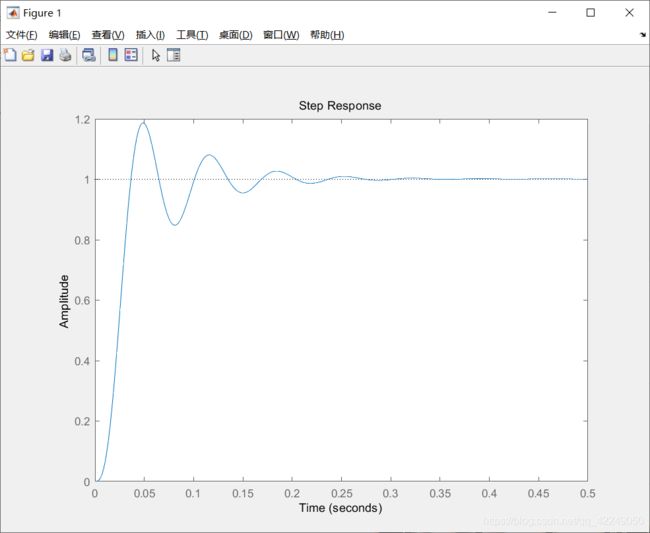
step(Target * sysResult,0.5); %串联并加入反馈后的传递函数阶跃
% %(仅绘制过渡过程的曲线,x坐标限制为[0,1])
% p1=plot(time,Target,'-.');
% xlim([0,0.5]);
% hold on;%指令信号的曲线(即期望输入)
% p2=plot(time,y);
% xlim([0,0.5]);
% hold on;%不含积分分离的PID曲线
Discrete_PID.m
clc;
clear;
Ts = 0.001; %采样时间=0.001s
sys = tf([0,300,200,350],[1,0.5,0.05,0]); %建立被控对象传递函数 无零点 极点为-10
dsys = c2d(sys,Ts,'z'); %将传递函数离散化 采样周期Ts
[num,den] = tfdata(dsys,'v'); %取出离散化后的传递函数参数
Error = 0; %当前偏差
ErrorLast = 0; %上次偏差
ErrorSum = 0; %累积偏差
u_1 = 0; %上时刻控制量
u_2 = 0; %上上时刻控制量
u_3 = 0; %上上上时刻控制量
y_1 = 0; %上时刻输出量
y_2 = 0; %上上时刻输出量
y_3 = 0; %上上上时刻输出量
y_4 = 0; %上上上上时刻输出量
%PID参数
Kp = 1.2;
Ki = 0.1;
Kd = 0.005;
u = zeros(1,1000); %预先分配内存
y = zeros(1,1000);
Target = zeros(1,1000); %目标值
time = zeros(1,1000);%时刻点(设定1000个)
for k = 1:1:1000
time(k) = k * Ts; %时间参数
Target(k) = 1000;
y(k) = num(4)*u_3 + num(3)*u_2 + num(2)*u_1 - den(4)*y_3 - den(3)*y_2 - den(2)*y_1;%系统响应输出序列
Error = Target(k) - y(k); %误差信号
u(k) = Kp*Error + Ki*ErrorSum + Kd*(Error - ErrorLast); %系统PID控制器输出序列
ErrorSum = ErrorSum + Error; %误差的累加和
u_3 = u_2;
u_2 = u_1;
u_1 = u(k); %前一个的控制器输出值
y_4 = y_3;
y_3 = y_2;
y_2 = y_1;
y_1 = y(k); %前一个的系统响应输出值
ErrorLast = Error; %前一个误差信号的值
end
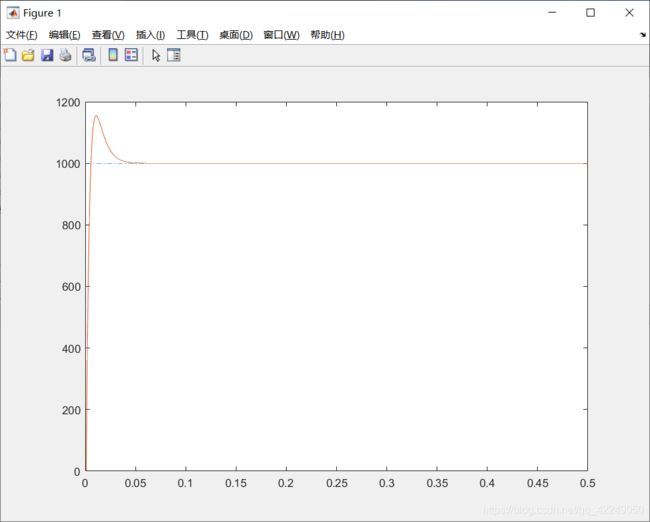
%(仅绘制过渡过程的曲线,x坐标限制为[0,1])
p1=plot(time,Target,'-.');xlim([0,0.5]);hold on;%指令信号的曲线(即期望输入)
p2=plot(time,y);xlim([0,0.5]);hold on;%不含积分分离的PID曲线
1.3 基于频域PID参数的Z-N整定
基于频域PID参数的Z-N整定可参考之前的博客文章,如下:
基于Ziegler-Nlichols 方法的PID参数整定
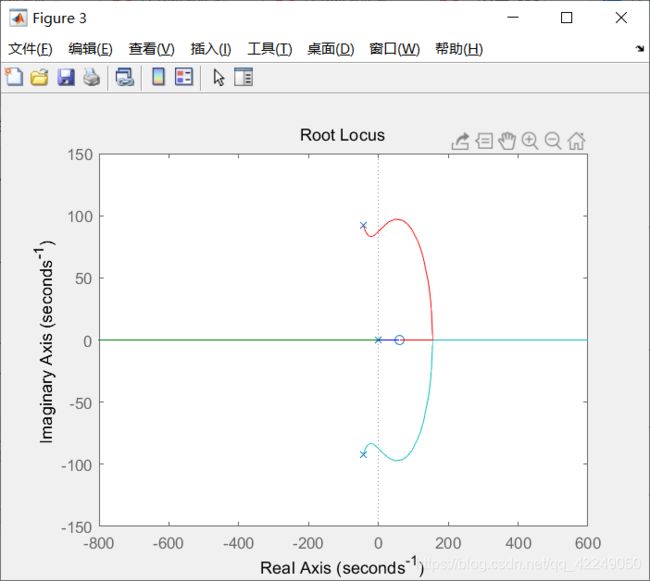
运行整定程序,可得图5~图。其中图5给出了系统未补偿的根轨迹图。
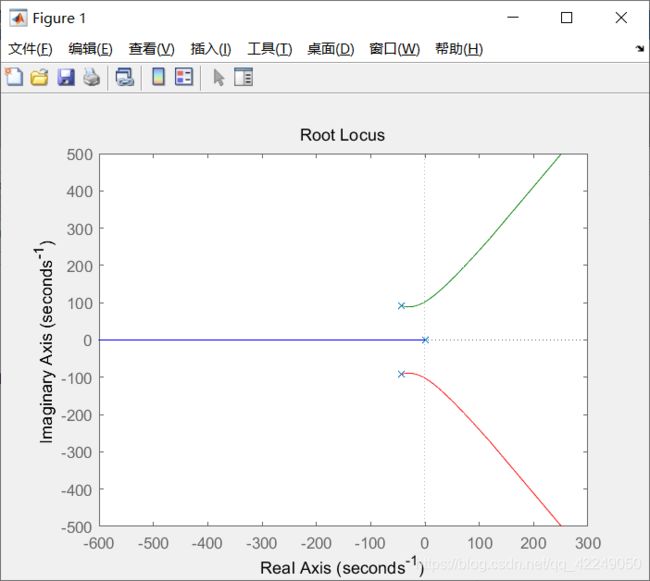
图5 系统未补偿的根轨迹图
需要在图5上可选定穿越虚轴时的增益Km和该点的wm值,即临界状态值。其中,整定程序中,sys_pid和sysc分别为控制器和闭环系统的传递函数。
图6 整定前后的系统Bode图
图6示出整定前后系统的伯特图,可见该系统整定后,频带拓宽,相移超前。
图7示出整定后系统的根轨迹,所有极点位于负半面,达到完全稳定状态。
%PID Controler Based on Ziegler-Nichols
clear all;
close all;
% sys=tf(400,[1,30,200,0]);
sys=tf(5.235e005,[1, 87.35, 1.047e004, 0]);
figure(1);
rlocus(sys);
[km,pole]=rlocfind(sys)
wm=imag(pole(2));
kp=0.6*km
kd=kp*pi/(4*wm)
ki=kp*wm/pi
figure(2);
grid on;
bode(sys,'r');
sys_pid=tf([kd,kp,ki],[1,0])
sysc=series(sys,sys_pid)
hold on;
bode(sysc,'b')
figure(3);
rlocus(sysc);
| 代码程序及仿真图 |
2模糊PID控制的设计
2.1 模糊PID控制律的设计
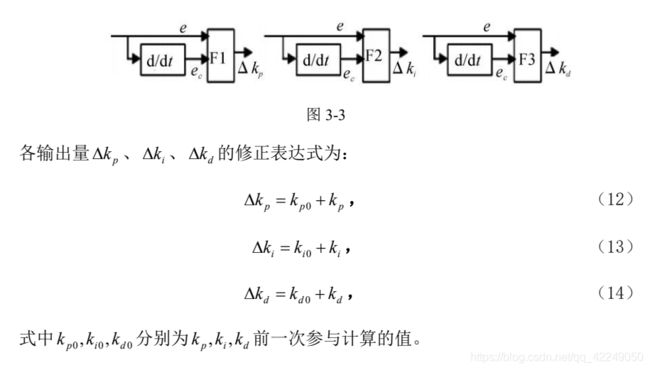
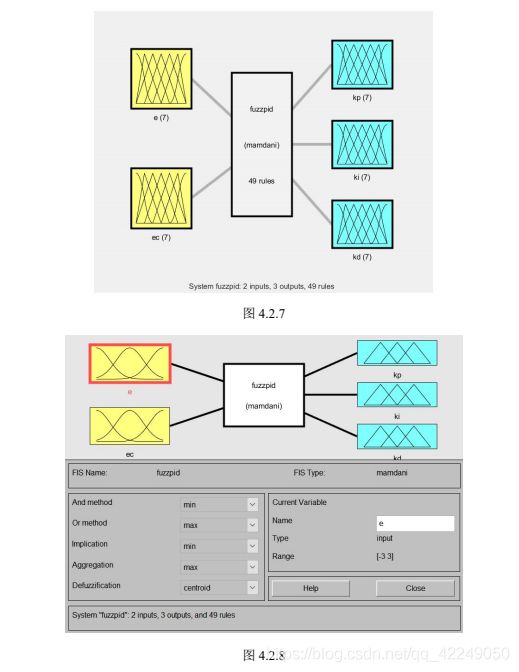
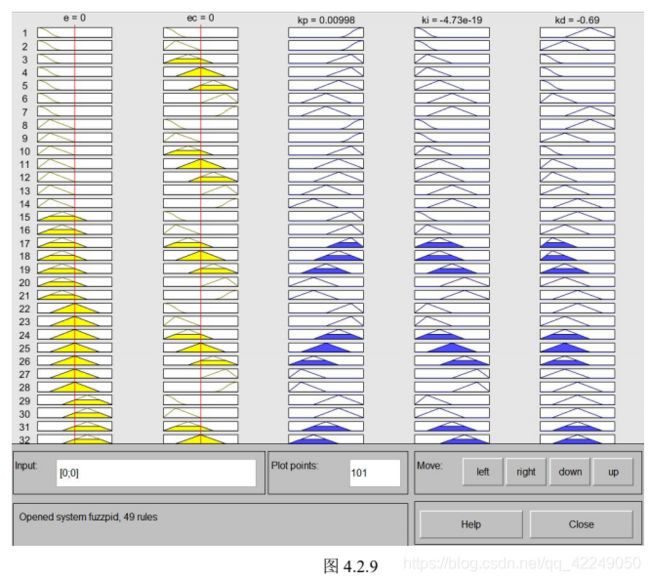
模糊自适应PID控制器是根据对输入信号的动态跟踪,采用模糊控制以及模糊推理,对PID的各个参数进行实时调整,实现在线整定的。它是模糊控制与传统PID控制的组合体,结合了各自的控制优点,为提高控制精度提供了充分的条件。其控制原理如图8所示。
2.2 模糊PID控制的仿真结果
| 代码程序及仿真图 |
3仿真对比与分析
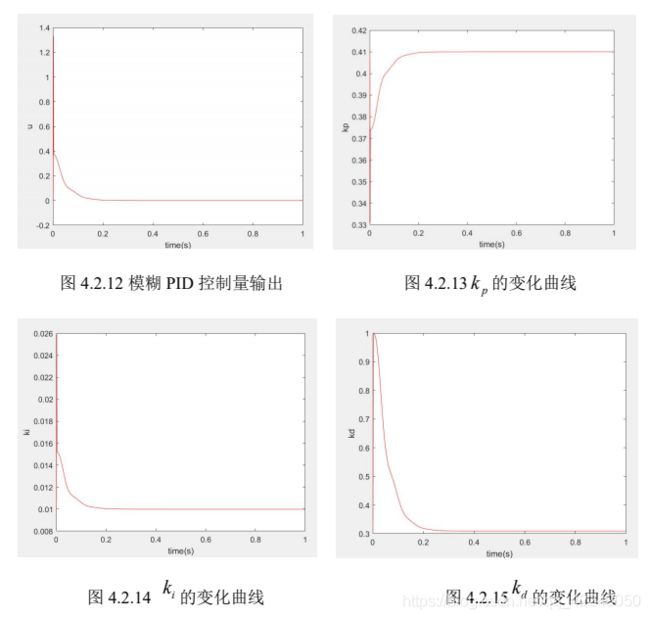
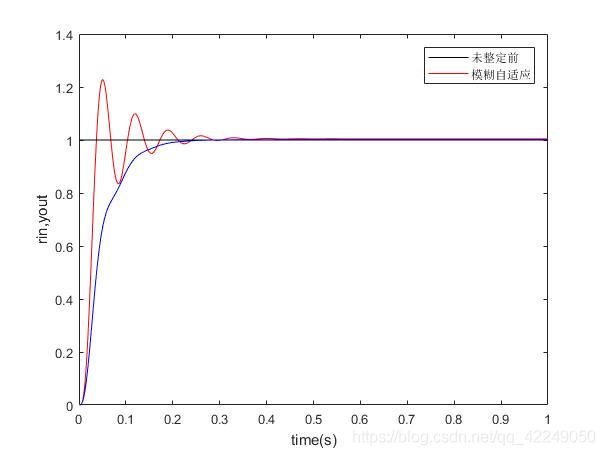
将模糊PID控制与传统PID控制的输出响应进行对比,可得:
| 代码程序及仿真图 |