这篇博客会介绍点云的基本知识,重点介绍最近两年发表的部分经典论文,有什么建议欢迎留言!
点云基本介绍
点云是某个坐标系下的点的数据集,包含了丰富的信息,可以是三维坐标X,Y,Z、颜色、强度值、时间等等。下面的图表分别展示了点云在三维空间可视化以后的效果和数据格式。点云的数据获取方式有很多种,比较常见的是三维激光扫描仪进行数据采集,它有三大类:
- 星载(星载LiDAR采用卫星平台,运行轨道高、观测视野广,基本可以测量到地球的每一个角落,为三维控制点和数字高程模型的获取提供了新的途径,有些星载激光雷达还具有观察整个天体的能力)
- 机载:机载主要借助无人机(UAV/UAS)进行大规模的点云数据采集。
- 地面分为三小种:地上三维激光扫描、车载MMS、手持激光扫描。
| x | y | z |
|---|---|---|
| 0.07388 | 0.16975 | -0.19326 |
| 0.15286 | 0.15050 | 0.24355 |
| 0.18606 | 0.15050 | 0.29081 |
从上面的数据示例可以看出,点云本质上是一长串点(Nx3矩阵,其中n是点数),这带来两个问题。第一,在几何上,点的顺序不影响它在空间中对整体形状的表示,例如,相同的点云可以由两个完全不同的矩阵表示,如下图所示。我们希望不论点云顺序怎样,模型可以从中得到相同的特征。第二,点云在空间中经过刚性变换后,如旋转或者平移,点云的坐标会变。有时我们为了方便对点云做处理(如分类等),需要将其旋转到正面或者侧面(做旋转),此时,模型得到的点云数据(N*3矩阵)将会完全不同。我们希望点云做变换之后不会影响模型的结果。
传统的点云处理方式包括两大类:
- 将点云数据投影到二维平面。此种方式不直接处理三维的点云数据,而是先将点云投影到某些特定视角再处理,如前视视角和鸟瞰视角。同时,也可以融合使用来自相机的图像信息。通过将这些不同视角的数据相结合,来实现点云数据的认知任务。比较典型的算法有MV3D和AVOD。
- 将点云数据划分到有空间依赖关系的体素(voxel)。此种方式通过分割三维空间,引入空间依赖关系到点云数据中,再使用3D卷积等方式来进行处理。这种方法的精度依赖于三维空间的分割细腻度,而且3D卷积的运算复杂度也较高。
接下来我们会介绍从17年至今比较经典的关于点云的论文,包括PointNet,PointNet++,GeoNet,Kd-Net、SO-Net以及做数据上采样的PU-Net。
PointNet
此处是PointNet的位置
PointNet++
此处是PointNet++的位置
GeoNet
- 论文名 GeoNet: Deep Geodesic Networks for Point Cloud Analysis
- 作者 Tong He,Haibin Huang,Li Yi等
GeoNet是一种基于测地距离的点云分析深度网络,发表在2019年的CVPR上。论文贡献包括两个:开发了一种数据表示以及提出了如何将其运用到下游任务中的方法。为了方便理解论文内容,我们首先来介绍一下测地距离这个概念。
测地距离
我们先从点云的研究任务说起。点云的形状分析是点云的重要任务之一,主要包括三个方面的特征,集合特征、统计特征和拓扑特征。集合特征主要有法向量、曲率等,统计特征主要包括模型顶点间的集合关系、顶点的曲率分布等,拓扑特征主要有突出的特征点、临界点、骨架、Reeb图等,其中骨架是对点云主要特征的一种可视化描述,符合人类的视觉特征。
从目前已有的工作来看,拓扑特征是点云的重要特征之一,对点云的分类、简化、检索等研究有重要的作用。寻找提取点云拓扑特征的简单、有效、快速的方法对点云的形状分析与理解具有重要的意义,测地线就是其中的一种。
测地线是连接曲面上给定的两点之间的最短路径,测地线的长度就是这两点之间的测地距离。根据计算结果的精确性,三维模型的测地距离的计算方法可以分为两大类:精确的方法和近似的方法。可以看做是图论上计算两个点之间的最短路径的计算方法,采用dijkstra等。
GeoNet计算测地距离
GeoNet其实就是利用网络来计算测地距离。我们假设\(\chi = \{ x_{i} \}\)表示点云,每个点的维度为3 。那么我们可以为点\(x_{i}\)定义它的邻居节点为\(B_{r}(x_{i})=\{ x_{j}|d_{E}(x_{i},x_{j}) \le r\}\) 。其中\(d_{E}(x_{i},x_{j})\)表示两个节点之间的欧式距离。也就是说将\(x_{i}\)为球心,半径为r内的节点划为它的邻居节点。这是GeoNet关于邻域的定义。基于此我们继续定义\(G_{r}(x_{i})=\{ g_{i,j}=d_{G}(x_{i},x_{j})|x_{j} \in B_{r}(x_{i}) \}\),其中\(d_{G}表示测地距离\),即\(G_{r}(x_{i})\)表示 \(x_{i}\)到邻域内每个点的测地距离的集合。GeoNet的目标是利用神经网络拟合映射关系:\(f:x_{i} \to G_{r}(x_{i})\),它的网络结构如下图所示。
如图所示,GeoNet由两个模块组成:特征提取模块以及测量匹配模块。其中特征提取模块利用PointNet++提取点云的局部特征,再将其输入解码器,同时还将原始的点云输入解码器(skip connection),这样解码器可以对点云的局部特征和总体特征做处理。测量匹配模块利用特征抽取模块得到的特征向量为每个节点计算其邻域测地距离。但该模块的目的并不是计算出准确的测地距离,而是在模型不断拟合测地距离的过程中,其参数矩阵会隐含的提取出一些特征。(笔者私以为,GeoNet的作用就是进行特征提取,在训练模型计算测地距离的过程中,模型的参数包含了点云的一些特征)
论文中还详细介绍了GeoNet如何与下游任务:分类、分割等做融合,并给出了示例。
Kd-Net
- 论文名 Escape from Cells: Deep Kd-Networks for the Recognition of 3D Point Cloud Models
- 作者 Roman Klokov,Victor Lempitsky
Kd-Net是一种基于Kd-tree的网络,我们先对Kd-tree加以介绍。
Kd-tree
KD树是从二叉搜索树发展来的,是一种高维索引树形数据结构,常用于大规模高维数据密集的查找比对的使用场景中,主要是最近邻查找以及近似最近邻查找,在CV中主要是图像检索和识别的高维特征向量的查找和比对。
我们举例讲述如何构建一个三维的KD树。我们可以在第一层选择用节点的第一维数据作为分类依据,第二层用第二维数据,第三层用第三维数据,第四层用第一维数据,以此类推。用图中的数据来说明:
- 根节点为(3,1,4),分类依据为3。
- 拿到第二个数据(2,3,7),先与根节点(3,1,4)比较,第一层节点的分类维度为一,(2,3,7)的第一维数据小于根节点的第一维数据,所以下一步与根节点的左节点做比较,发现左节点为空,将(2,3,7)放在左节点。
拿到第三个数据(2,1,3),先与根节点(3,1,4)比较,第一层节点的分类维度为一,(2,1,3)的第一维数据小于根节点的第一维数据,所以下一步与根节点的左节点做比较。左节点为(2,3,7),第二层节点的分类维度为二,(2,1,3)的第二维数据比(2,3,7)的第二维数据小,下一步与其左节点作比较。左节点为空,将(2,1,3)插入该点。
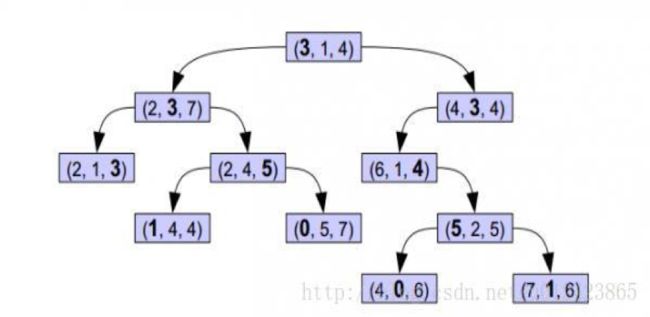
KD树构建过程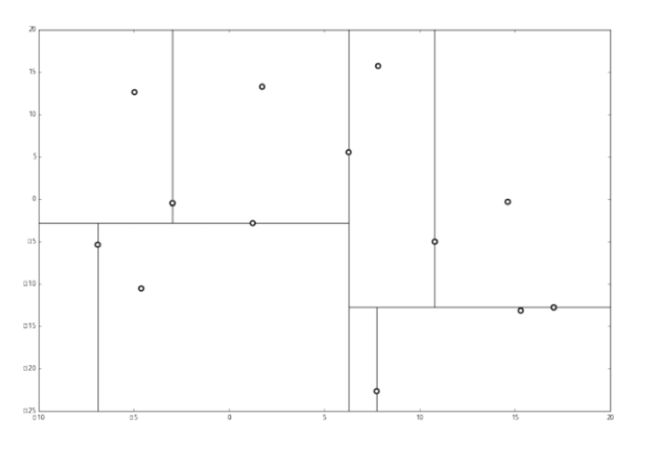
二维KD树的表示方法利用Kd_tree构建Kd-net
了解了如何构建Kd-tree后,我们来看如何根据点云构建Kd-tree进一步组成Kd-net。
下图左边是建好的Kd-tree,编号为8-15的是8个数据点。可以看到紫色的是第一次切割,蓝色和红色是第二层,绿色和橙色(或红色?)是第三层。该示意图用二维展示了三维点云的kd-tree,在三维空间中,切割的方向是x,y,z轴。为了将点云向量化,作者先用预训练好的数据将叶子节点(8、9、12、13、14、15)向量化,然后根据公式逐层向上计算每个节点的向量表示,直到所有的节点都被向量化。
图中的右半部分是Kd-net的结构图,其中灰色的条表示网络的节点,中间的圆圈是网络的参数,第一层是所有数据点的向量表示。网络经过一次前向传播得到一个特征向量,即图中标号为1的节点,该节点提取了所有数据的特征。标号为1的特征向量经过一个全连接层得到节点0,即分类结果。其中,相同颜色的圆圈表示网络中的共享参数。节点之间共享参数的条件为:在Kd-tree中是同一层,且分割的方向都相同。可以看到节点8、9、12、13、14、15在同一层且分割的方向都相同:平行于y轴。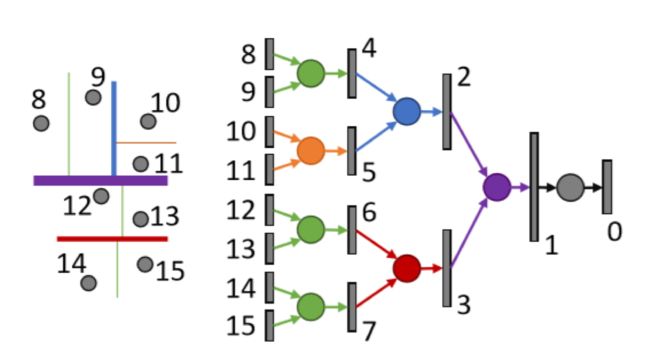
kd-tree和kd-net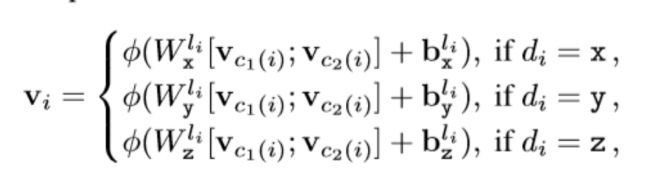
kd-tree向量化公式
SO-Net
- 论文名 SO-Net: Self-Organizing Network for Point Cloud Analysis
- 作者 Jiaxin Li ,Ben M.Chen Gim Hee Lee
SO-Net是一种用于无序点云深度学习的置换不变网络结构。它有如下两个特点:
- SO-Net通过构建自组织映射(SOM)来模拟点云的空间分布。
- 基于SOM,SO-Net对单个点和SOM节点进行分层特征提取,最终用单个特征向量来表示输入点云。
在识别点云重建,分类,对象部分分割和形状检索等任务中,So-Net网络表现出的性能与最先进的方法相似或更好。另外,由于所提出的架构的并行性和简单性,所以训练速度比现有的点云识别网络快得多。这篇论文发表在2018年的CVPR上。
理解这篇文章的重点在于了解自组织网络,我们先介绍什么是自组织网络,再进一步介绍自组织网络如何应用到点云数据上。
自组织网络
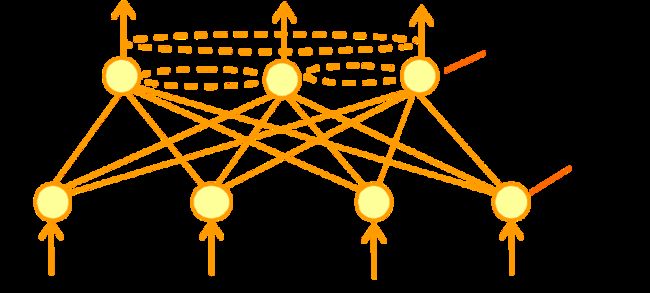
自组织(竞争型)神经网络的结构一般由输入层和竞争层构成,两层之间的各个神经元实现双向连接,而且网络之间没有隐含层,有时候竞争层各个神经元之间还存在横向连接,其结构图如下所示。学习算法上,它模拟生物神经元之间的兴奋、协调与抑制、竞争等作用的信息处理来指导神经元竞争对输入模型响应的机会,最后仅有一个神经元称为竞争的胜利者,这一神经元则表示对输入模型的分类。SOM一般可以用于分类和聚类等任务。
SOM是一种自组织神经网络,它定义了独特的激活神经元选择策略、权重调整方法等。SOM的最重要的特点是可以做保序映射。1989年Kohonen给出一个SOM网的著名应用实例:把不同的动物按照其属性映射到二维输出平面上,使属性相同的动物在SOM网输出平面上的位置也相近。每种动物的输入为一个29维的向量,前16个分量采用独热编码,代表当前输入的是哪一个动物,后13个分量是该动物的属性值。最终的输出结果如下图所示,可以看出,属性相同的动物挨在一起。即SOM将输入空间压缩并保留其拓扑空间映射在二维平面上。因此SOM可以用于数据压缩和特征提取等任务。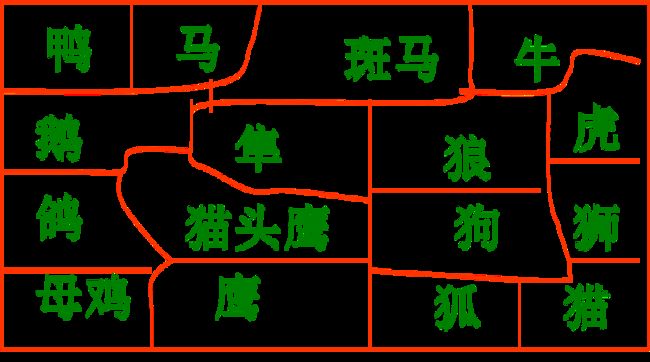
我们可以用一个例子形象化的理解SOM拟合数据的过程。如下图所示,蓝色部分是训练数据的分布,白色的小点是从该分布中抽取得到的当前训练数据。首先SOM随机的分布在数据空间中,我们选择最接近当前训练数据的SOM作为获胜节点,用黄色突出显示。选出获胜节点后,我们更新获胜节点及其周围节点的参数,如图中的第二个状态所示,获胜节点及其周围节点被拉向训练数据。经过都次迭代后,SOM网格趋向于接近训练数据的分布。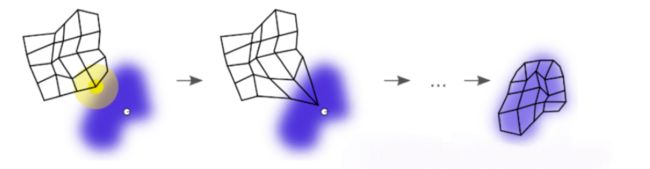
SO-Net
将SOM应用到点云数据上,效果如下图所示。可以看到,刚开始SOM数据点是随机分布在空间中,经过一段时间的训练可以可以拟合三维飞机形状的数据分布。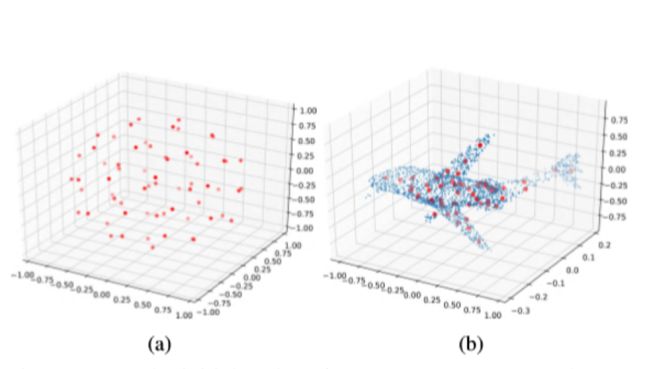
可知,SOM可以拟合点云的数据分布。基于此,作者设计了SO-Net,具体结构如下图所示。输入N3的点云数据,构建mm的SOM矩阵提取数据特征后,经过归一化,特征提取,和池化等操作后,得到m*384的特征矩阵,在经过全连接层和池化层,得到输入数据的特征向量,进一步做分类和分割。
(这边的具体过程没太看懂,感觉论文讲的有点混乱,符号似乎也有点问题,比如在做归一化的时候,是不是km*3?如果有看懂的小伙伴请留言谢谢!)
PU-Net
- 论文名 PU-Net: Point Cloud Upsampling Network
- 作者 Lequan Yu,Xianzhi Li,Chi-Wing Fu等
PU-Net在点云上进行上采样,即输入一个点云,输出一个更密的点云,且它落在输入点云隐含的几何体(比如表面)上。PU-Net的核心思想,是学习到每个点多个粒度(从局部到全局)下的特征,再在特征空间中扩大点集,最后将扩大的点集映射回三维。提取特征的方法基于PointNet++。其网络结构如下图所示: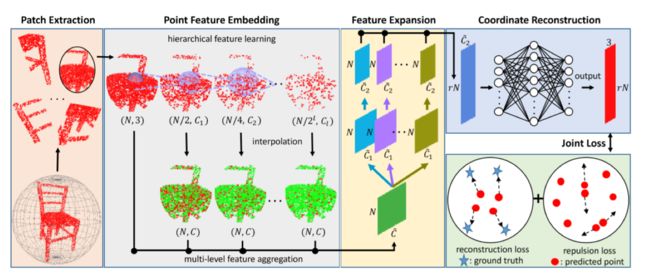
如图所示,PU-Net主要分为四个过程:
- Patch Extraction:这一过程其实是提取点云的若干个部分。在模型表面上随机选择M个中心点,然后指定一个测地线距离d,将测地线距离范围内的点和中心点一起作为一个Patch。采用不同的测地线距离d可以形成不同尺寸的patch。
- Point Feature Embedding:这一过程包括两个阶段,特征提取和特征融合。PU-Net采用PointNet++进行特征提取,即先对数据进行下采样,然后学习特征。针对多个层次的特征,PU-Net采用三元插值算法进行特惠装呢个融合,图中绿色的部分即为通过红色的数据点插值得到的数据。
- Feature Expansion:特征扩展的目的是将NC的特征矩阵扩展为rNC,其中r是上采样率。我们可以先将NC扩展到rNC,在通过两个11的卷积核学习特征,再合并为一个rNC2的特征矩阵。
- Coordinate Reconstruction:坐标重建的过程是将扩大的特征空间再映射回三维空间的过程。通过多个全连接层,将rNC2的矩阵转化为rN3。
在这个过程中,值得一提的是,PU-Net为了使新生成的点均匀分布在数据表面,设计了两种损失函数:
- 重建损失:为了使数据分布在数据模型表面。采用Earth Move Distance衡量生成的点云和ground truth之间的距离。其中\(\phi\)是一个从生成点云到ground truth的双射函数。
公式为:\[L_{rec}=d_{EMD}(S_{p},S_{gt})=min_{\phi : S_{p}\to S_{gt}} \sum_{x_{i}\in S_{p}} \| x_{i}-\phi(x_{i}) \|_{2}\] - 排斥损失:如果只有重建损失,那么从一个点派生出来的r个点可能会聚集在一起,为了使这些点分开,需要增加排斥损失,其中距离越大,公式中的权重越大。
公式为:\[L_{rep}=\sum^{\hat{N}}_{i=0} \sum_{i'\in K(i)} \eta (\| x_{i'} -x_{i}\|)w(\| x_{i'}-x_{i} \|)\]
总损失的计算公式为:
\[L(\theta )= L_{rec}+\alpha L_{rep} +\beta \| \theta \|^{2}\]
其中\(\beta \| \theta \|^{2}\)是正则化项。
PU-Net的效果图如下所示:
可以看出,它可以补全数据点中残缺的部分,上采样的效果非常好。
持续更新...
