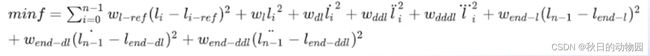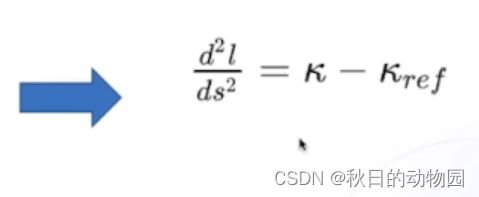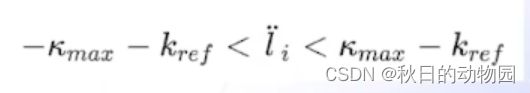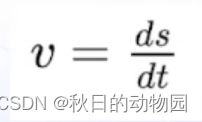3.路径规划算法解析及实现
星火计划2.0基础课:https://apollo.baidu.com/community/online-course/2
星火计划2.0专项课:https://apollo.baidu.com/community/online-course/12
APOLLO中Planning主要分为两个步骤:
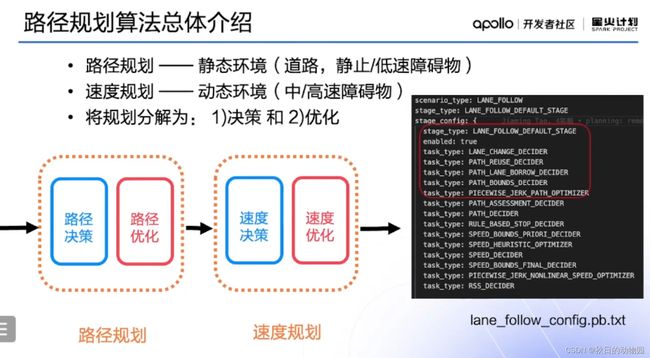
首先进行路径规划,然后进行速度规划。对于路径规划主要是针对于静态环境的规划,比如道路、静止或低速的障碍物,会产生对障碍物进行绕行的路径;对于速度规划,主要是针对于动态环境的规划,比如道路中中高速的障碍物,会对障碍物产生绕行或超越。主路的规划算法任务配置在lane_follow_config.pb.txt这个配置文件中,该配置文件首先进行路径规划,即红框中内容,其中所有以DECIDER为结尾的,都是Apollo中的决策器,所有以OPTIMIZER为结尾的都是Apollo中的优化器。路径规划和速度规划每个又分为两个部分,一个是决策和优化,先进行路径决策再进行路径优化,先进行速度决策,再进行速度优化。
现在来具体讲一下其中每一个task是做什么的:
第一个Task是LANE_CHANGE_DECIDER,主要是换道的决策,首先会判断由参考线生成器产生的参考线的数量,如果只有一条参考线就不会进行换道,如果参考线生成器产生多条的参考线,还会继续判断换道的条件,比如车辆的前方和后方有没有障碍物,或者旁边车道有没有障碍物,是否达到了换道的距离,当所有条件满足后,里面会产生一个换道的决策。
第二个Task是PATH_REUSE_DECIDER是路径重用的决策,主要可以判断是否可以重用上一帧的路径,因为路径规划中每一帧都在进行规划,假如感知到障碍物边界不稳定,那么每一帧规划路径会随着障碍物的边界会上下跳动,这样会带来的问题就是行驶上的不稳定,路线也会跟着障碍物进行上下跳动。所以Apollo设计了一种路径重用的决策,如果上一帧路径没有与障碍物发生碰撞就会复用上一帧的路径,这样就不会进行上述的重新路径规划了,会直接跳到速度规划部分,如果上一帧路径和障碍物存在碰撞,就会进行重新路径规划。
第三个Task是PATH_BORROW_DECIDER是否借道的决策,主要是处理自车道前方有一个阻挡自车行驶的障碍物的场景,它会来决策是否要借助旁边车道来进行绕行,这里决策也是要一些判断的条件,比如是否只有一条车道,如果只有一条车道就没法借道了,比如自车前方是否有左侧道路的障碍物,这个障碍物是否远离路口,如果这个障碍物离路口比较近,就不会产生一个借道的决策。这个障碍物是否是长期存在的,就避免其是一个临时停车的障碍物,这个障碍物是否是长期存在的,就排除其是一个临时停车的障碍物,以及旁边车道是实线还是虚线,当条件满足后会产生一个向左或者向右借道的决策。
下一个决策:
Task是PATH_BOUNDS_DECIDER,主要处理的是SL坐标系内确定车辆可行驶的确定边界,即路径可以走的边界范围,会利用前几个决策,产生对于每个候选路径的边界。
下一个是优化算法:
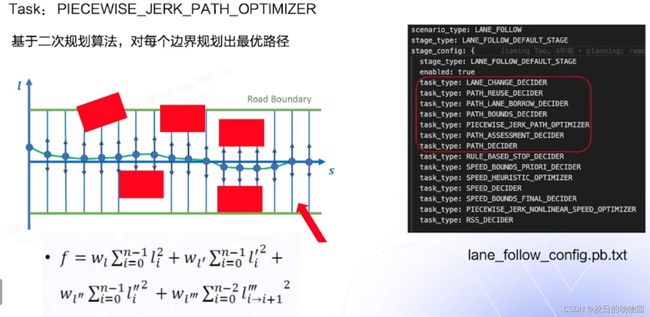
Task:PIECEWISE_JERK_PATH_OPTIMIZER对每个边界规划出一个最优的路径,规划出一条没有碰撞且平滑的路径,这个算法后面会详细的介绍。
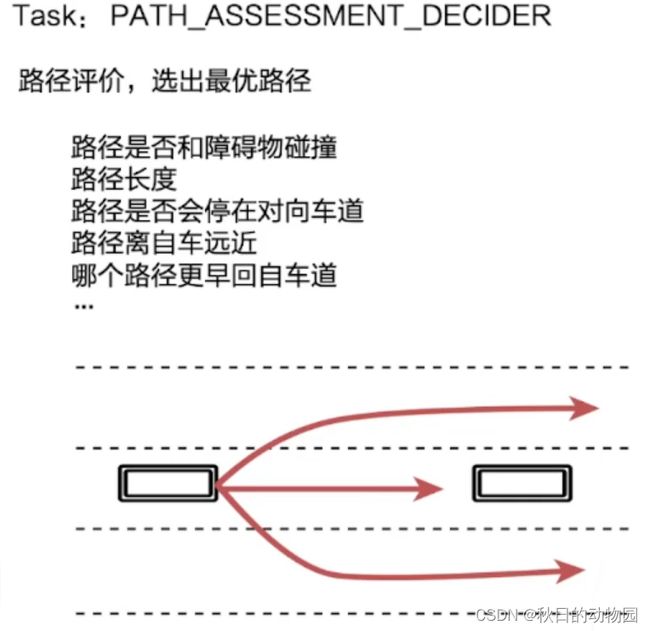
算法会对每一个决策产生一个最优的路径,PATH_ASSESSMENT_DECIDER,会对路径进行评价,会从路径中选出一条最优的路径,最优路径的选择也是遵循一些规则,比如路径是否会对障碍物碰撞,如果会碰撞就会排除该路径;路径长度,哪一条路径更短;路径是否会停在对向车道上,哪条路径可以更早的回到自车道上。
Task是PATH_DECIDER,是对每个障碍物去赋予决策,如上图所示,对于前方障碍物选择绕行,对于左前方障碍物,选择停止。该决策主要用于速度规划上。
下面来讲解基于二次规划的路径规划算法
二次规划是用于求解目标函数为二次型的,约束为线性约束的问题。二次规划的标准型如上图所示。其中x为优化的变量,我们要求解满足最小值时的x,其是一组n维的向量,P是一个二次项的系数,其为一个正定矩阵,正定是为了保证xTPx大于0,才能有极小值点。q为n维的实数向量,A为m*n的矩阵,m是约束函数的个数,A为约束函数一次项的系数,l和u分别是m维的向量,主要是约束函数取得了上边界和下边界。
二次规划是成熟的一类优化问题,里面有很多现成的开源求解器,比如osqp,qpOASES.
对于所有二次规划问题,其设计步骤都是一样的。
首先定义优化变量(即标准型里的x),然后设计目标函数,然后设计约束,最后代入求解器求解。
接下来看Apollo的二次规划算法是如何设计的。
首先定义优化变量,由于路径规划算法在参考线的frenet坐标系进行规划,采用,s和l分别表示沿着参考线和垂直参考线的坐标,然后将障碍物分别投影到sl坐标系上
即把S这条线拉直了,在s方向分别以固定的间隔▲s选取路径规划的点,比如s0,s1,s2…..sn-1,从0到n-1就是路径规划的长度。选取每个间隔点对应的l作为优化的变量,再将l的一阶导和二阶导也作为优化的变量,最后就会得到x(二次规划的优化向量),其包含了三个部分:l,一阶导,二阶导
定义完优化变量,来设计目标函数:
首先来表述期望路径是什么样的:
因此可以得到目标函数:
对每个点cost求和,前面的w为对应的惩罚项。其中包含一个对三阶导的惩罚,三阶导由以下公式求得:
目标函数一次项,二次项系数(q,P)以矩阵形式表示为:
接下来讲解二次函数的约束是如何设置的:
路径规划首先要满足一些硬性的约束要求
其次要根据当前状态,满足主车的横向速度/加速度/加加速度的运动学限制要求:
首先要讲一下对于曲率的约束,因为车辆行驶时有着最大曲率的限制,根据曲率的坐标转换公式(Frenet公式),l的二阶导和轨迹的曲率有一些关系,但是这里没办法直接得到曲率的公式应用于约束函数。因为约束函数只能做一次项,所以要对曲率和二阶导的函数关系进行简化,首先需要做一些假设,假设轨迹几乎沿着参考线规划:
假设θ-θref等于0.
由于曲率实际上是很小的,远远小于1,所以两个曲率相乘可以近似看作0.
则此时二阶导的公式简化为:
由车辆运动学可知,车辆可行驶的最大曲率为:
(最大前轮转角除以轴距),前轮最大转角对于每个车辆也是固定的,其和方向盘转角存在一个固定比例的关系。则二阶导的约束为:
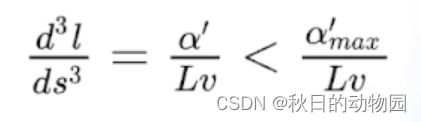
另外轨迹还要满足曲率变化率的要求,即使得曲率变化率满足方向盘能打得过来。
这里还要做一些假设:
同时假设,速度是恒定的:
然后代入三阶导公式,即:
最后总结一下:
即每个点的二阶导要是连续的,同时也要可导的。(三阶导积分可以得到二阶导,二阶导积分可以得到一阶导,一阶导积分可以得到l,所以每两个点之间的三阶导值是恒定的,二阶导,一阶导的值是连续可导的,所以这样的一个曲线就是每两个点之间满足三阶导恒定的多项式的关系式)
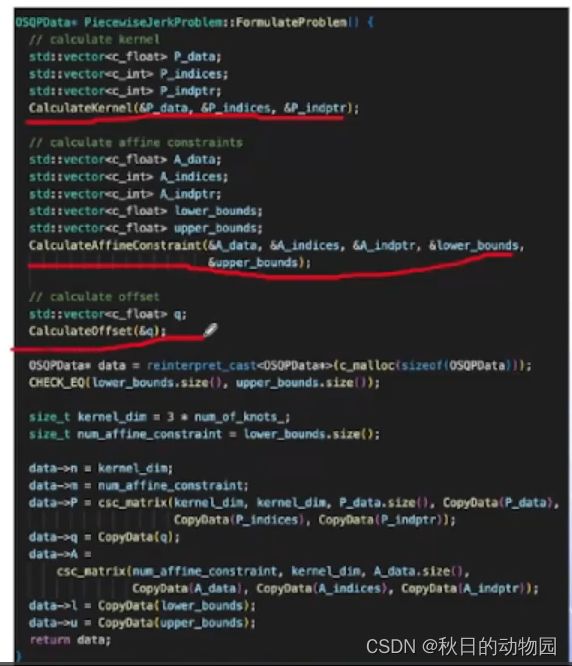
将优化变量的约束和等式约束转化为约束矩阵A
其分别包含,l,一阶导,二阶导,三阶导,然后是满足运动学连续的函数关系式,最后是起点的硬性约束。
最后将算法代入求解器求解:
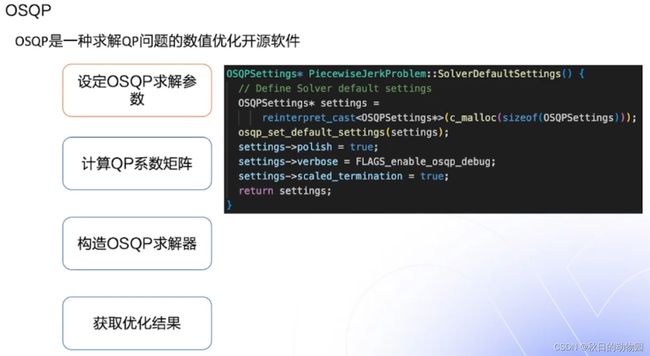
求解主要包括了四个步骤,第一步是设置求解器的参数,在SolverDefaultSettings里面包含了一些求解器的默认参数。
然后是计算Q,P系数矩阵,即计算二次规划的q和p的系数。
红线是分别计算P,A和q的系数的函数。
计算完之后,构造OSQP求解器进行求解:
主要通过调用osqp_setup这个函数,把数据导进去就可以自动进行求解。
最后获取优化结果:
红线分别是获得优化值,获得优化变量的取值。
接下来讲解路径规划算法的执行过程:
整个路径规划首先从参考线平滑开始,首先其会产生ReferenceLineInfo这样一个类,保存所有的ReferenceLine的计算结果。接下来在路径规划部分按顺序依次执行每个任务。这里的任务包含了决策器和优化器的任务,这里每个决策器或优化器的入口函数都是Process函数:
求解的结果保存在reference_line或reference_line_info中。
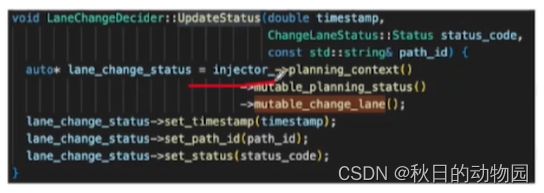
第一个换道决策器,主要产生是否换道的状态:
主要产生是否换道的状态,它产生的状态会保存在injector中,其在planning中是一个单一类,其保存的变量会贯穿planning始终,也就是可以在不同帧之间进行共用。(因为换道也是要贯穿好几帧进行的决策)
接下来是借道决策,其保存的变量在reference_line_info中,如果产生借道决策,后面的值设置为true,另外会把借道的状态向左或向右保存到injector中
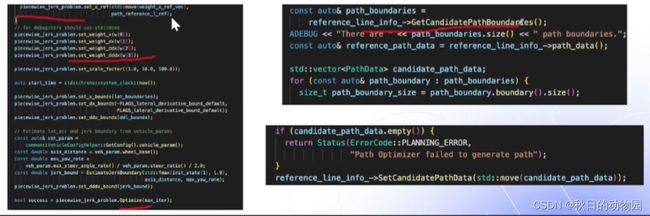
第三步是产生路径边界,根据现有决策在参考线上采样,获得每个点的在l方向上的可行驶区域,其包含了四种边界:
最后将所有路径边界通过setCandidatePathBoundarier保存在reference_line_info中
接下来是路径优化
其主要通过调用piecewise_jerk_problem去进行优化求解(其是二次规划求解器的一个类),这里会设置二次优化问题的一个权重以及一些约束,最后调用Optimize函数去进行一个优化的求解。这里通过从reference_line_info获得候选路径,把每条路径生成的边界,保存在该变量中。
最后选择最优路径,其会调用ComparePathData函数,两两比较每一条path哪个更优,将最优的path保存在reference_line_info中(mutable_path_data中),同时把这个path中阻塞的最近的障碍物放入blocking_obstacle中,也是供速度规划进行进一步的处理。