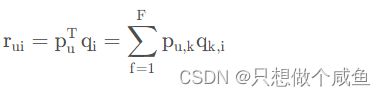矩阵分解(MF):MATRIXFACTORIZATIONTECHNIQUES FORRECOMMENDERSYSTEMS
一、前言
上篇文章提到UserCF and Item CF (Collaborative Filtering)_只想做个咸鱼的博客-CSDN博客
协同过滤的缺点是,头部效应较为明显且泛化能力较弱的问题,矩阵分解算法被提出,加入了隐向量的概念,加强模型处理稀疏矩阵的能力
下面让我们一起来看一下什么是隐向量及怎么用隐向量
二、MF算法概念
1、隐向量
矩阵分解算法是期望为每一个用户和物品生成一个隐向量,将用户和物品定位到隐向量的表示空间上,用隐向量表达的物品和用户,还要保证相似的用户及用户可能喜欢的物品距离相近,那么我们就可以基于隐向量得到用户对于物品的评分矩阵。
在矩阵分解的算法框架下, 我们就可以通过分解协同过滤的共现矩阵来得到用户和物品的隐向量, 就是上面的用户矩阵Q和物品矩阵P, 这也是“矩阵分解”名字的由来。
矩阵分解算法将m × n 维的共现矩阵R(这个就是我们在协同过滤时用到的用户—物品评分矩阵,也叫“共现矩阵”)分解成m × k 维的用户矩阵U和k × n维的物品矩阵V 相乘的形式。 其中m是用户数量, n是物品数量, k是隐向量维度,也就是隐含特征个数, 只不过这里的隐含特征变得不可解释了, 即我们不知道具体含义了,要模型自己去学。k的大小决定了隐向量表达能力的强弱, k越大,表达信息就越强,理解起来就是把用户的兴趣和物品的分类划分的越具体了嘛。
比较通俗点就是,从原来的一个矩阵,分解为两个矩阵,这两个矩阵里面的参数是可以不断自己学习的,学完之后的参数通过矩阵乘法可以得到任何一个位置的评分,通过已有的评分,不断更新参数的值,达到预测没有评分的位置预测
那么如果有了用户矩阵和物品矩阵的话, 我们就知道了如果想计算用户u 对物品i的评分,只需要
2、矩阵分解算法的求解
(1)梯度下降算法
求解上面两个矩阵的参数问题转换成一个最优化问题, 可以通过训练集里面的观察值利用最小化来学习用户矩阵和物品矩阵
所以上述的公式可以完善为
三、代码实现
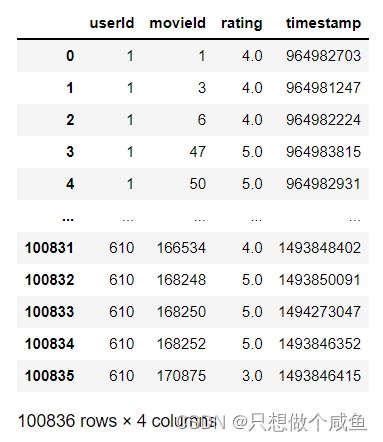
1、数据集加载
这里用的和CF模型中一样的数据集,这里就不细致展出了,就简单看下数据集
然后划分训练集与验证集
# 声明两个字典, 分别是训练集和测试集
trainSet, testSet = {}, {}
trainSet_len, testSet_len = 0, 0
pivot = 0.75 # 训练集的比例
# 遍历data的每一行, 把userId, movidId, rating按照{user: {movidId: rating}}的方式存储, 当然定义一个随机种子进行数据集划分
for ele in data.itertuples(): # 遍历行这里推荐用itertuples, 比iterrows会高效很多
user, movie, rating = getattr(ele, 'userId'), getattr(ele, 'movieId'), getattr(ele, 'rating')
if random.random() < pivot:
trainSet.setdefault(user, {})
trainSet[user][movie] = rating
trainSet_len += 1
else:
testSet.setdefault(user, {})
testSet[user][movie] = rating
testSet_len += 1
print('Split trainingSet and testSet success!')
print('TrainSet = %s' % trainSet_len)
print('TestSet = %s' % testSet_len)2、创建矩阵分解模型
这里用基础的SVD试试, 也就是那个带正则和偏置的那个
class BasicSVD():
def __init__(self, rating_data, F=5, alpha=0.1, lmbda=0.1, max_iter=100):
self.F = F # 这个表示隐向量的维度
self.P = dict() # 用户矩阵P 大小是[users_num, F]
self.Q = dict() # 物品矩阵Q 大小是[item_nums, F]
self.bu = dict() # 用户偏差系数
self.bi = dict() # 物品偏差系数
self.mu = 0.0 # 全局偏差系数 这个目前没看出咋用的!!先留个点
self.alpha = alpha # 学习率
self.lmbda = lmbda # 正则项系数
self.max_iter = max_iter # 最大迭代次数
self.rating_data = rating_data # 评分矩阵
# 初始化矩阵P和Q, 方法很多, 一般用随机数填充, 但随机数大小有讲究, 根据经验, 随机数需要和1/sqrt(F)成正比
cnt = 0 # 统计总的打分数, 初始化mu用
for user, items in self.rating_data.items():
self.P[user] = [random.random() / math.sqrt(self.F) for x in range(0, F)] #对每一个用户的隐向量进行初始化
self.bu[user] = 0 #用户的偏差系数,初始为0
cnt += len(items)
for item, rating in items.items():
if item not in self.Q: ##对每一个物品的隐向量进行初始化
self.Q[item] = [random.random() / math.sqrt(self.F) for x in range(0, F)]
self.bi[item] = 0 #物品的偏差系数,初始为0
self.mu /= cnt
# 有了矩阵之后, 就可以进行训练, 这里使用随机梯度下降的方式训练参数P和Q
def train(self):
for step in range(self.max_iter): #最大迭代次数,也就是将整个数据重复训练多少遍
for user, items in self.rating_data.items():
for item, rui in items.items():
rhat_ui = self.predict(user, item) # 得到预测评分
# 计算误差
e_ui = rui - rhat_ui # rui 就是我们的评分矩阵存在的评分、rhat_ui就是我们隐向量P和Q的向量积
#更新用户和物品的偏差系数
self.bu[user] += self.alpha * (e_ui - self.lmbda * self.bu[user])
self.bi[item] += self.alpha * (e_ui - self.lmbda * self.bi[item])
# 随机梯度下降更新梯度 这里就是对参数进行更新了
for k in range(0, self.F):
self.P[user][k] += self.alpha * (e_ui*self.Q[item][k] - self.lmbda * self.P[user][k])
self.Q[item][k] += self.alpha * (e_ui*self.P[user][k] - self.lmbda * self.Q[item][k])
self.alpha *= 0.1 # 每次迭代步长要逐步缩小
# 预测user对item的评分, 这里没有使用向量的形式,和向量的矩阵乘法是一样的效果
def predict(self, user, item):
return sum(self.P[user][f] * self.Q[item][f] for f in range(0, self.F)) + self.bu[user] + self.bi[item] + self.mu
basicsvd = BasicSVD(trainSet, F=128)
basicsvd.train()这里说一下,F是隐向量的维度,我们具体输出user1看其隐向量的表示到底是什么(128太大了,我们这里改维度F=10,用以参考)
下面的数据就是user1的初始化隐向量的维度刚好是1*10,这里面也就是可以不断更新的参数
1: [0.030410184824286854, 0.05412486151665668, 0.14351522500992048, 0.19807034805744658, 0.14439483649227738, 0.255954620835901, 0.06096894470856824, 0.16150007964543955, 0.14266109415662817, 0.06683358841095748],
3、产生推荐列表
# 这里产生推荐列表, 遍历物品列表, 如果用户看了, 那么就跳过, 否则, 预测用户对该电影的打分, 然后记录, 最后排名
movie_list = []
for user, items in trainSet.items():
for item in items.keys():
if item not in movie_list:
movie_list.append(item)
def recommend(aim_user, n=10):
rank = {}
watched_movies = trainSet[aim_user] # 目标用户看过的电影,也就是训练集中的items ID, 我们将预测测试集中的item ID
for movie in movie_list: #保证推荐的电影是我们训练集中存在的电影,也就是训练过的电影
if movie in watched_movies: #保证将要推荐的电影不能是该用户在训练集中看过的电影,也就是给他推荐其他没看过的电影
continue
# 如果当前用户没看过, 就预测打分, 并保存到rank
rank[movie] = basicsvd.predict(aim_user, movie)
return sorted(rank.items(), key=lambda x: x[1], reverse=True)[:n] 这是针对user3产生的10个推荐(通过评分的高低排序而来)
4、推荐结果的指标
# 准确率、召回率和覆盖率
n = 10 # 推荐用户评分高的前10部
hit = 0
rec_count = 0 # 统计推荐的影片数量, 计算查准率
test_count = 0 # 统计测试集的影片数量, 计算查全率
all_rec_movies = set() # 统计被推荐出来的影片个数, 无重复了, 为了计算覆盖率
item_populatity = dict() # 计算新颖度
# 先计算每部影片的流行程度
for user, items in trainSet.items():
for item in items.keys():
if item not in item_populatity:
item_populatity[item] = 0
item_populatity[item] += 1 # 这里统计训练集中每部影片用户观看的总次数, 代表每部影片的流行程度
# 计算评测指标
ret = 0
ret_cou = 0
for user, items in trainSet.items(): # 这里得保证测试集里面的用户在训练集里面才能推荐
test_movies = testSet.get(user, {})
rec_movies = recommend(user)
for movie, w in rec_movies:
if movie in test_movies:
hit += 1
all_rec_movies.add(movie)
ret += math.log(1+item_populatity[movie])
ret_cou += 1
rec_count += n
test_count += len(test_movies)
precision = hit / (1.0 * rec_count)
recall = hit / (1.0 * test_count)
coverage = len(all_rec_movies) / len(item_populatity)
ret /= ret_cou*1.0
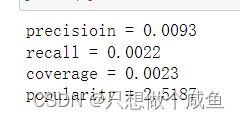
print('precisioin = %.4f\nrecall = %.4f\ncoverage = %.4f\npopularity = %.4f' % (precision, recall, coverage, ret))四、总结
1、矩阵分解的优缺点
优点:与CF相比
泛化能力强,空间复杂度低、更好的扩展性和灵活性
缺点:
矩阵分解同样不方便加入用户、物品和上下文相关的特征
2、后续的改进
逻辑回归模型及后续发展的因子分解机等模型,凭借融合不同特征的能力,逐渐得到了更广泛的应用,接下来我们也会出后续的模型,尽请期待!!!
论文推荐:MATRIXFACTORIZATIONTECHNIQUES FORRECOMMENDERSYSTEMS