Python机器学习基础教程2
文章目录
-
-
- 朴素贝叶斯分类器
-
- 优点缺点和参数
- 决策树
-
- 报错
- 构造决策树
- 控制决策树的复杂度
- 树的特征重要性
- 回归决策树
- 优点缺点
- 决策树集成
-
- 1.随机森林
-
- 构造随机森林
- 优点缺点
- 1.梯度提升回归树(梯度提升机)
-
- 优点缺点
-
朴素贝叶斯分类器
朴素贝叶斯分类器是与线性模型非常相似的一种分类器,他的训练速度更快,但是她的泛化能力比线性分类器稍差。朴素贝叶斯模型高效的原因在于,它通过单独查看每个特征来学习参数,并从每个特征中搜集简单的类别统计数据。scikit-learn中实现了三种朴素贝叶斯分类器:GaussianNB、BernoulliNB 和 MultinomialNB。GaussianNB 可 应 用 于 任 意 连 续 数 据, 而BernoulliNB 假定输入数据为二分类数据,MultinomialNB 假定输入数据为计数数据(即每个特征代表某个对象的整数计数,比如一个单词在句子里出现的次数)BernoulliNB 和MultinomialNB 主要用于文本数据分类。
BernoulliNB 分类器计算每个类别中每个特征不为 0 的元素个数:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import mglearn
# 4个数据点,每个点有4个二分类特征,
x = np.array([
[0,1,0,1],
[1,0,1,1],
[0,0,0,1],
[1,0,1,0]
])
# 两个类别0和1
y = np.array([0,1,0,1])
counts = {}
for label in np.unique(y):
# 对每个类别进行遍历
# 计算(求和)每个特征中1的值
# sum(axis = 0)对[]内最大块按行计算
counts[label] = x[y == label].sum(axis = 0)
print("feature counts{}".format(counts))
运行结果:
feature counts{0: array([0, 1, 0, 2]), 1: array([2, 0, 2, 1])}
MultinomialNB 计算每个类别中每个特征的平均值,而 GaussianNB 会保存每个类别中每个特征的平均值和标准差。
优点缺点和参数
MultinomialNB 和 BernoulliNB 都只有一个参数 alpha,用于控制模型复杂度。alpha 的工作原理是,算法向数据中添加 alpha 这么多的虚拟数据点,这些点对所有特征都取正值。这可以将统计数据“平滑化”(smoothing)。alpha 越大,平滑化越强,模型复杂度就越低。
算法性能对 alpha 值的鲁棒性相对较好,也就是说,alpha 值对模型性能并不重要。但调整这个参数通常都会使精度略有提高。
GaussianNB 主要用于高维数据,而另外两种朴素贝叶斯模型则广泛用于稀疏计数数据,比如文本。
MultinomialNB 的性能通常要优于 BernoulliNB,特别是在包含很多非零特征的数据集(即大型文档)上。
决策树
决策树广泛用于分类和回归任务的模型,本质上,它从一层层的if/else问题中进行学习,并得出结论。
mglearn.plots.plot_animal_tree()
def plot_animal_tree(ax=None):
import graphviz
if ax is None:
ax = plt.gca()
mygraph = graphviz.Digraph(node_attr={'shape': 'box'},
edge_attr={'labeldistance': "10.5"},
format="png")
mygraph.node("0", "Has feathers?")
mygraph.node("1", "Can fly?")
mygraph.node("2", "Has fins?")
mygraph.node("3", "Hawk")
mygraph.node("4", "Penguin")
mygraph.node("5", "Dolphin")
mygraph.node("6", "Bear")
mygraph.edge("0", "1", label="True")
mygraph.edge("0", "2", label="False")
mygraph.edge("1", "3", label="True")
mygraph.edge("1", "4", label="False")
mygraph.edge("2", "5", label="True")
mygraph.edge("2", "6", label="False")
mygraph.render("tmp")
ax.imshow(imread("tmp.png"))
ax.set_axis_off()
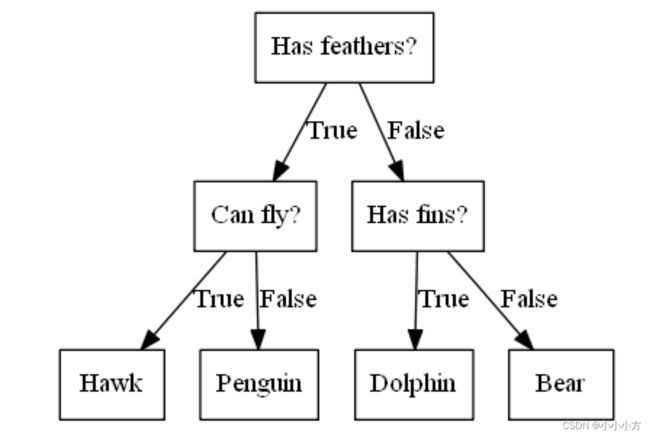
树的每个结点代表一个问题或一个包含答案的最终结点,树的边将问题的答案与将问的下一个问题连接起来。
报错
graphviz包不存在
1.在电脑安装graphviz软件,配置环境变量
2.在虚拟环境中直接安装
构造决策树
使用数据集two_moons,每个数据集由2个半月形组成,每个类别都包含50个数据点。学习决策树就是学习一系列if/else问题,使我们能够以最快的速度得到正确答案,在ML中这些问题叫做测试。
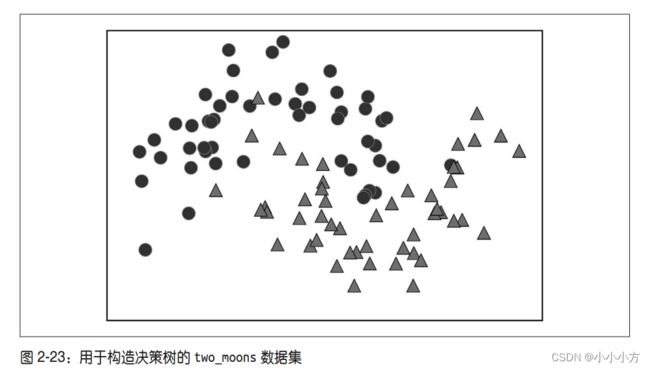
为了构造决策树,算法搜索遍所有可能的测试,找出对目标变量来说信息量最大的那一个。

上图为选出的第一个测试,将数据集在x[1]=0.596处垂直划分可以得到最多的信息,它在最大程度上将类别0和类别1中的点进行区分。顶结点表示整个数据集。在两个区域中重复寻找最佳测试,构建更准确的模型。
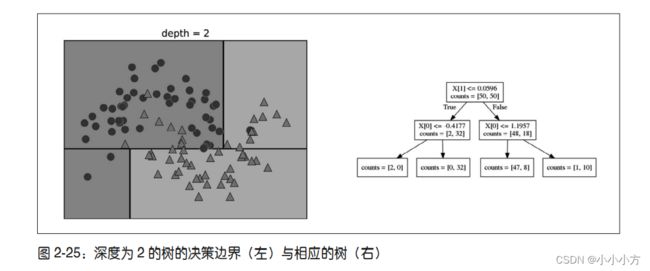
上图是第二次划分,这次划分是基于x[0]做出的,分为左右两个区域。这一递归过程生成一颗二元决策树,其中每个结点都包含一个测试,或者你可以将每个测试看成沿着一条轴对当前数据进行划分,每个测试仅关注一个特征,所以划分后的区域边界始终与坐标轴平行。对数据反复进行递归划分,直到划分后的每个区域(决策树的每个叶结点)只包含单一目标值(单一类别或单一回归值)。如果树中某个叶结点所包含数据点的目标值相同,那么这个叶结点是纯的。
two_moons数据集最终划分结果:
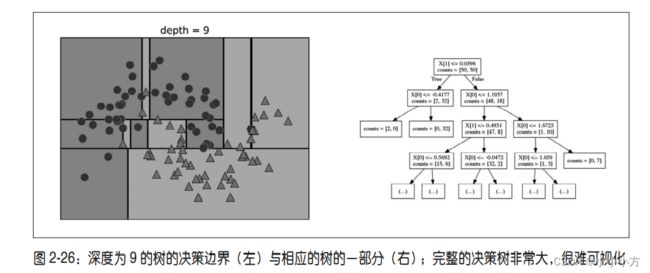
想要对数据点进行测试,首先查看这个点位于特征空间划分的哪个区域,然后将该区域的多数目标值(如果是纯的叶节点,就是单一目标值)作为预测结果,从根节点开始对树进行遍历就可以找到这一区域,每一步向左还是向右都取决于是否满足相应的测试。
决策树任务也可以用于回归任务,预测的方法是基于每个结点的测试对树进行遍历,最终找到新数据点所属的页结点,这一数据点的输出即为此叶结点中所有训练点的平均目标值。
控制决策树的复杂度
构造决策树直到所有的叶结点都是纯的叶结点,会导致模型非常复杂,并且对训练数据高度过拟合,纯叶结点的存在说明这棵树在训练集上的精度是100%。
防止过拟合的常见策略:
1.及早停止树的生长,称为预剪枝,预剪枝的限制条件可能包括限制树的最大深度,限制叶结点的最大数目,或者规定一个结点中数据点的最小数目来防止继续划分
2.先构造树,随后删除或折叠信息量很少的结点,称为后剪枝
在乳腺癌数据集上看预剪枝的效果:
from sklearn.tree import DecisionTreeClassifier
cancer = load_breast_cancer()
x_train,x_test,y_train,y_test = train_test_split(
cancer.data,cancer.target,stratify=cancer.target,random_state=42
)
# 使用默认配置 树完全展开
tree = DecisionTreeClassifier(random_state=0)
tree.fit(x_train,y_train)
print("accuracy on training set:{:.3f}".format(tree.score(x_train,y_train)))
print("accuracy on test set:{:.3f}".format(tree.score(x_test,y_test)))
# 使用预剪枝 max_depth = 4
tree = DecisionTreeClassifier(max_depth=4,random_state=0)
tree.fit(x_train,y_train)
print("accuracy on training set:{:.3f}".format(tree.score(x_train,y_train)))
print("accuracy on test set:{:.3f}".format(tree.score(x_test,y_test)))
运行结果:
accuracy on training set:1.000
accuracy on test set:0.937
accuracy on training set:0.988
accuracy on test set:0.951
利用tree模块中的export_graphviz函数将树可视化,此函数生成一个.dot格式的文件,这是一种用于保存图形的文本文件格式
# 将决策树可视化
from sklearn.tree import export_graphviz
export_graphviz(tree,out_file="tree.dot",class_names=["malignant","benign"],feature_names=cancer.feature_names,impurity=False,filled=True)
# 使用graphviz模块读取这个文件并将其可视化
import graphviz
with open("tree.dot") as f:
dot_graph =f.read()
graphviz.Source(dot_graph).view()

树的可视化有助于深入理解算法是如何进行预测的,找出大部分数据的实际路径有利于更好的观察树。
树的特征重要性
可以利用一些有用的属性来总结决策树,最常用的是特征重要性,他为每个特征对树的决策的重要性进行排序,对于每个特征来说,它都是介于0和1之间的数字。
print("feature importance:\n{}".format(tree.feature_importances_))
运行结果:
feature importance:
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0.01019737 0.04839825
0. 0. 0.0024156 0. 0. 0.
0. 0. 0.72682851 0.0458159 0. 0.
0.0141577 0. 0.018188 0.1221132 0.01188548 0. ]
特征重要性可视化
# 特征重要性可视化
def plot_feture_importances_cancer(model):
n_features = cancer.data.shape[1]
# 创建水平条形图,正常的柱状图旋转了
180
plt.barh(range(n_features),model.feature_importances_,align='center')
plt.yticks(np.arange(n_features),cancer.feature_names)
plt.xlabel("feature importance")
plt.ylabel("feature")
plt.show()
plot_feture_importances_cancer(tree)
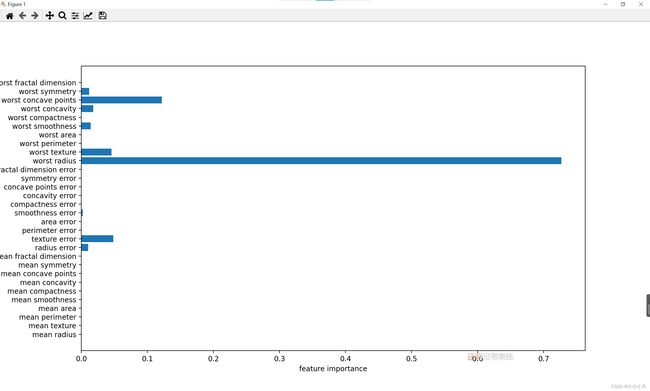
特征重要性始终为整数,不能说明该特征对应哪个类别,特征重要性只能说明这个特征很重要,并没有告诉问半径大表示样本是良性还是恶性。在特征和类别之间的关系并没有很简单。
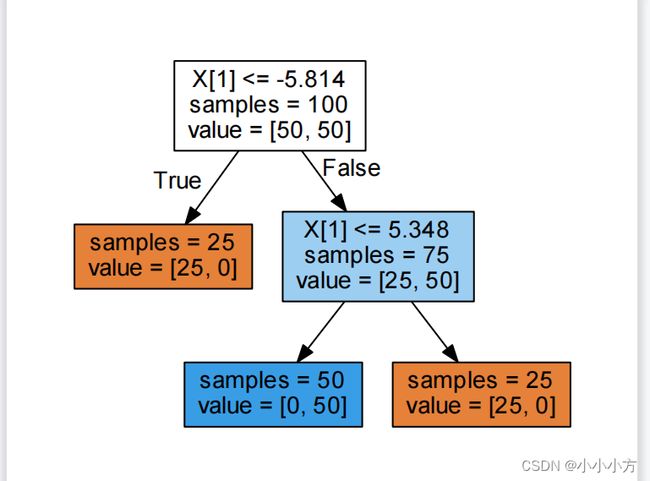
tree = mglearn.plots.plot_tree_not_monotone()
plt.show()
运行结果:
Feature importances: [0. 1.]
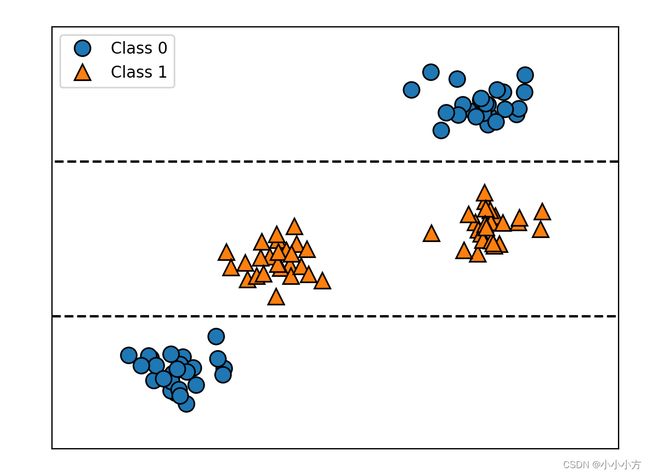
y轴上的特征与类别标签是非单调的关系,以及决策树给出的决策边界
with open("mytree.dot") as f:
dot_graph = f.read()
graphviz.Source(dot_graph).view()
该图显示的是有两个特征和两个类别的数据集。这里所有信息都包含在 X[1] 中,没有用到X[0]。但 X[1] 和输出类别之间并不是单调关系,即我们不能这么说:“较大的 X[1] 对应类别 0,较小的 X[1] 对应类别 1”(反之亦然)。
回归决策树
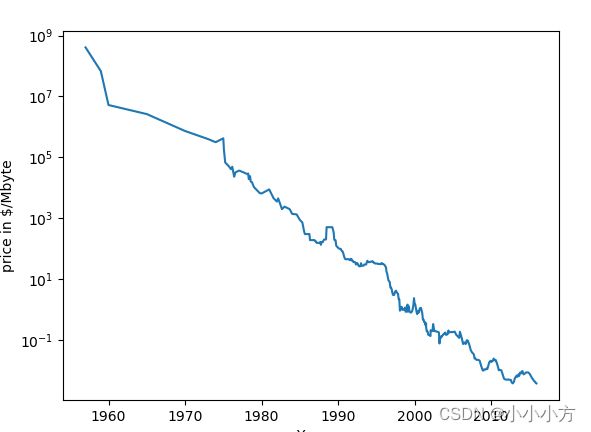
将基于树的模型用于回归时,不能外推也不能在训练数据范围之外进行预测。
import pandas as pd
import matplotlib.pyplot as plt
ram_prices = pd.read_csv("data/ram_price.csv")
plt.semilogy(ram_prices.date,ram_prices.price)
plt.xlabel("Year")
plt.ylabel("price in $/Mbyte")
plt.show()
# 使用2000年之前的历史数据预测2000年后的价格,只用日期做特征
# 对整个数据集进行预测,为了定量评估,只考虑测试数据集
from sklearn.tree import DecisionTreeRegressor
# 利用历史数据预测2000年后的价格
data_train = ram_prices[ram_prices.date < 2000]
data_test = ram_prices[ram_prices.date >= 2000]
# 基于日期来预测价格
# np.newaxi将一维数据转换成二维数据
x_train = data_train.date[:,np.newaxis]
# 利用对数变换得到数据和目标之间更简单的关系
y_train = np.log(data_train.price)
# 进行对比的两个模型
tree = DecisionTreeRegressor().fit(x_train,y_train)
linear_reg = LinearRegression().fit(x_train,y_train)
# 对所有数据进行预测
x_all = ram_prices.date[:,np.newaxis]
pred_tree = tree.predict(x_all)
pred_lr = linear_reg.predict(x_all)
# 对数变换逆运算
price_tree = np.exp(pred_tree)
price_lr = np.exp(pred_lr)
# 将决策树和线性回归模型的预测结果与真实值进行对比
# semilogy()函数将使用 y 轴的对数刻度绘制数据
plt.semilogy(data_train.date,data_train.price,label="training data")
plt.semilogy(data_test.date,data_test.price,label="test data")
plt.semilogy(ram_prices.date,price_tree,label="tree prediction")
plt.semilogy(ram_prices.date,price_lr,label="linear prediction")
plt.legend()
plt.show()
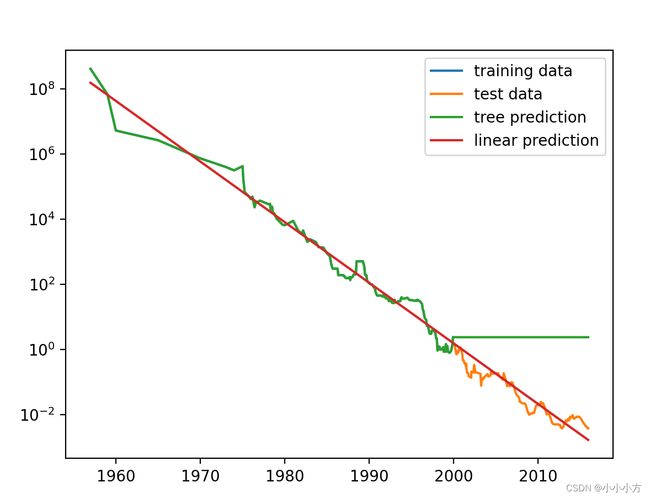
利用2000年之前的历史数据来预测2000年后的价格,只用日期作为特征,对价格取对数使得两者的关系的线性相对更好,对整个数据集进行测试,两个模型之间的差异非常明显,线性模型用一条直线对数据做近似,这条直线对2000年后的数据给了相当好的训练数据,忽略了训练数据和测试数据中的一些更细微的变化。树模型完美预测了训练数据,没有对树的复杂度进行限制,树模型记住了整个训练数据集,一旦输入超出了训练模型的数据的范围,模型就只能持续预测最后一个已知的数据点,树不能在训练数据的范围之外生成新的相应,所有基于树的模型都有这个缺点。
优点缺点
控制决策树模型复杂度的参数是预剪枝参数,它在树完全展开之前停止树的构造。通常来说,选择一种预剪枝策略(设置 max_depth、max_leaf_nodes 或 min_samples_leaf)足以防止过拟合。
决策树有两个优点:一是得到的模型很容易可视化,非专家也很容易理解(至少对于较小的树而言);二是算法完全不受数据缩放的影响。由于每个特征被单独处理,而且数据的划分也不依赖于缩放,因此决策树算法不需要特征预处理,比如归一化或标准化。特别是特征的尺度完全不一样时或者二元特征和连续特征同时存在时,决策树的效果很好。决策树的主要缺点在于,即使做了预剪枝,它也经常会过拟合,泛化性能很差。
决策树集成
集成是合并多个机器学习模型来构建更强大模型的方法。有两种集成模型对大量分类和回归数据集都是有效的,随机森林和梯度提升决策树,二者都是以决策树为基础。
1.随机森林
决策树的一个主要缺点在于经常对训练数据过拟合。随机森林是解决这个问题的一种方法。随机森林本质上是许多决策树的集合,其中每棵树都和其他树略有不同。随机森林背后的思想是,每棵树的预测可能都相对较好,但可能对部分数据过拟合。如果构造很多树,并且每棵树的预测都很好,但都以不同的方式过拟合,那么我们可以对这些树的结果取平均值来降低过拟合。既能减少过拟合又能保持树的预测能力,这可以在数学上严格证明。
我们需要构造许多决策树。每棵树都应该对目标值做出可以接受的预
测,还应该与其他树不同。随机森林的名字来自于将随机性添加到树的构造过程中,以确保每棵树都各不相同。随机森林中树的随机化方法有两种:一种是通过选择用于构造树的数据点,另一种是通过选择每次划分测试的特征。
构造随机森林
想要构造一个随机森林的模型,需要确定用于构造树的个数,这些树在构造的时候是彼此完全独立,算法对每棵树进行不同的随机选择,确保树和树之间是有区别的。
首先对数据进行自助采样,从n_sample个数据点中有放回的重复随机抽取一个样本,抽取n_sample此,创建一个与原数据集大小相同的数据集,但有些数据点会缺失或重复。
接下来基于这个新创建的数据集来构造决策树,在每个结点处,算法随机选择特征的一个子集,并对其中的一个特征寻找最佳测试,而不是对每个结点都找寻最佳测试,选择的特征的个数是有max_features参数来控制,每个结点中特征子集的选择是相互独立的,这样树的每个结点可以使用特征的不同子集来做出决策。由于使用了自助采样,随机森林中构造每棵决策树的数据集都是略有不同的,由于每个结点的特征选择,每棵树中的每次划分都是基于特征的不同子集,这两种方法共同保证随机森林中所有树都不一样。
想要利用随机森林进行预测,首先对森林中的每棵树进行预测,对于回归问题,对这些结构取平均值作为最终预测,对于分类,则用到了“软投票”的预测概率取平均值,然后将概率最大的类别作为预测结果。
将5棵树组成的随机森林作用到two_moons数据上:
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
import mglearn
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons
from linearClassify import cancer
x,y = make_moons(n_samples=100,noise=0.25,random_state=3)
x_train,x_test,y_train,y_test = train_test_split(x,y,stratify=y,random_state=42)
forest = RandomForestClassifier(n_estimators=5,random_state=2)
forest.fit(x_train,y_train)
# 作为随机森林的一部分,树被保存在estimator_属性中
# 将每棵树学到的决策边界可视化,也将它们的总预测(整个森林做出的预测)可视化
fig,axes = plt.subplots(2,3,figsize=(20,10))
# enumerate实现即遍历索引又遍历元素
# ravel() 将数据打散为一维数组
for i,(ax,tree) in enumerate(zip(axes.ravel(),forest.estimators_)):
ax.set_title("tree{}".format(i))
mglearn.plots.plot_tree_partition(x_train,y_train,tree,ax=ax)
mglearn.plots.plot_2d_separator(forest,x_train,fill=True,ax=axes[-1,-1],alpha=0.4)
axes[-1,-1].set_title("random forest")
mglearn.discrete_scatter(x_train[:,0],x_train[:,1],y_train)
plt.show()
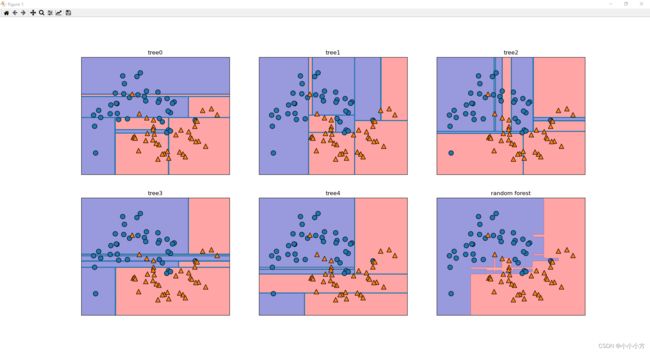
五张图学到的决策边界大不相同,每棵树都犯了一些错误,因为这里画出的一些训练点实际上并没有包含在这些树的训练集中,原因在于自助采样。随机森林比单独每一颗树的过拟合都要小,给出的决策边界也更符合直觉,使用更多的决策树,可以得到更平滑的边界。
# 将包含100棵树的随机森林应用在乳腺癌的数据集上
x_train,x_test,y_train,y_test = train_test_split(cancer.data,cancer.target,random_state=0)
forest = RandomForestClassifier(n_estimators=100,random_state=0)
forest.fit(x_train,y_train)
print("accuracy on training set:{:.3f}".format(forest.score(x_train,y_train)))
print("accuracy on test set:{:.3f}".format(forest.score(x_test,y_test)))
运行结果:
accuracy on training set:1.000
accuracy on test set:0.972
在没有任何参数的情况下下,随机森林的精度为97%,比线性模型或单颗决策树都要好。
与决策树类似,随机森林也可以给出特征重要性,计算方式是将森林中所有树的特征重要性求和取平均,一般来说,随机森林给出的特征重要性比单颗树给出的更为可靠。
def plot_feature_importances_cancer(model):
n_features = cancer.data.shape[1]
# 柱状图
plt.barh(np.arange(n_features), model.feature_importances_, align='center')
# yticks函数作用是获取或设置y坐标轴的刻度及标签。
plt.yticks(np.arange(n_features), cancer.feature_names)
plt.xlabel("Feature importance")
plt.ylabel("Feature")
plt.ylim(-1, n_features)
plot_feature_importances_cancer(forest)
plt.show()
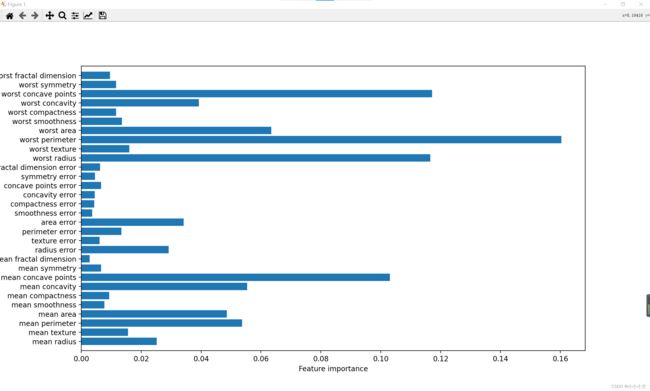
与单棵树相比,随机森林中有更多特征重要性不为0,与单棵决策树类似,随机森林也给了“worst radius”(最大半径)特征很大的重要性,但从总体来看,它实际上却选择“worst perimeter”(最大周长)作为信息量最大的特征。由于构造随机森林过程中的随机性,算法需要考虑多种可能的解释,结果就是随机森林比单棵树更能从总体把握数据的特征。
优点缺点
随机森林拥有决策树的所有优点,但仍然使用决策树的一个原因是hi需要决策过程的紧凑表示,基本上不可能对几十棵甚至上百棵树做出详细的解释,随机森林中树的深度往往比决策树要大。
随机森林本质是随机的,设置不同的随机状态可以彻底改变构建的模型,森林中的树越多,对随机状态选择的鲁棒性就越好,如果希望结果重现,固定random_state。
对于维度非常高的稀疏数据,随机森林的表现往往不是很好,对于这种数据,使用线性模型可能更合适。即使是非常大的数据集,随机森林的表现通常也很好,训练过程很容易并行在功能强大的计算机的多个CPU内核上,但是随机森林需要更大的内存,训练和预测的速度也比线性模型要慢。
需要调节的重要参数有n_estimators和max_features,可能还保活预剪枝选项(max_depth)。n_estimators总是越大越好,对更多的树取平均可以降低过拟合,从而得到更好的集成,但是收益是递减的,树越多需要的内存越多,训练时间越长,在内存、时间允许的情况下尽量的多。
max_fetures决定每棵树的随机性的大小,较小的max_features可以降低过拟合。一般来说就是使用默认值:对于分类,默认值是 max_features=sqrt(n_features);对于回归,默认值是max_features=n_features。增大 max_features 或 max_leaf_nodes 有时也可以提高性能。它还可以大大降低用于训练和预测的时间和空间要求。
1.梯度提升回归树(梯度提升机)
梯度提升回归树是另一种集成方法,通过合并多个决策树来构建一个更为强大的模型。虽然名字中含有“回归”,但这个模型既可以用于回归也可以用于分类。与随机森林方法不同,梯度提升采用连续的方式构造树,每棵树都试图纠正前一棵树的错误。默认情况下,梯度提升回归树中没有随机化,而是用到了强预剪枝。梯度提升树通常使用深度很小(1到 5 之间)的树,这样模型占用的内存更少,预测速度也更快。
梯度提升背后的主要思想是合并许多简单的模型(在这个语境中叫作弱学习器),比如深度较小的树。每棵树只能对部分数据做出好的预测,因此,添加的树越来越多,可以不断迭代提高性能。与随机森林相比,它通常对参数设置更为敏感,但如果参数设置正确的话,模型精度更高。
除了预剪枝与集成中树的数量之外,梯度提升的另一个重要参数是 learning_rate(学习率),用于控制每棵树纠正前一棵树的错误的强度。较高的学习率意味着每棵树都可以做出较强的修正,这样模型更为复杂。通过增大 n_estimators 来向集成中添加更多树,也可以增加模型复杂度,因为模型有更多机会纠正训练集上的错误。
# 梯度提升回归树
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
import mglearn
# 在乳腺癌数据集上,默认使用100棵树,最大深度是3,学习率是0.1
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import load_breast_cancer
cancer =load_breast_cancer()
x_train,x_test,y_train,y_test = train_test_split(cancer.data,cancer.target,random_state=0)
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(x_train,y_train)
print("accuracy on training set:{:.3f}".format(gbrt.score(x_train,y_train)))
print("accuracy on test set:{:.3f}".format(gbrt.score(x_test,y_test)))
运行结果:
accuracy on training set:1.000
accuracy on test set:0.965
可能存在过拟合,限制最大深度来加强预剪枝,也可以降低学习率
# 限制最大深度
gbrt = GradientBoostingClassifier(random_state=0,max_depth=1)
gbrt.fit(x_train,y_train)
print("accuracy on training set:{:.3f}".format(gbrt.score(x_train,y_train)))
print("accuracy on test set:{:.3f}".format(gbrt.score(x_test,y_test)))
# 降低学习率
gbrt = GradientBoostingClassifier(random_state=0,learning_rate=0.01)
gbrt.fit(x_train,y_train)
print("accuracy on training set:{:.3f}".format(gbrt.score(x_train,y_train)))
print("accuracy on test set:{:.3f}".format(gbrt.score(x_test,y_test)))
运行结果:
accuracy on training set:0.991
accuracy on test set:0.972
accuracy on training set:0.988
accuracy on test set:0.965
降低模型复杂度的两种方法都降低了训练集的精度,减小树的最大深度显著提升了模型性能,降低学习率提高了模型的泛化能力。
对于其他基于决策树的模型,我们也可以将特征重要性可视化,可以更好理解模型,因为可视化所有的决策树是不现实的。
# 特征重要性可视化
gbrt = GradientBoostingClassifier(random_state=0,max_depth=1)
gbrt.fit(x_train,y_train)
def plot_feature_importances_cancer(model):
n_features = cancer.data.shape[1]
plt.barh(np.arange(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), cancer.feature_names)
plt.xlabel("Feature importance")
plt.ylabel("Feature")
plt.ylim(-1, n_features)
plt.show()
plot_feature_importances_cancer(gbrt)
优点缺点
梯度提升决策树是监督学习中最强大也是最常用的模型之一,缺点是需要仔细调参,而且训练时间可能会比较长,与其他基于树的模型类似,这一算法不需要对数据进行缩放就可以表现的很好,而且也适用于二元特征与连续特征同时存在的数据集,与其他基于树的模型相同,他也通常不适用于高维稀疏数据。
梯度提升树的模型主要参数包括树的数量和学习率(用于控制每棵树对前一棵树的错误的纠正强度)这两个参数高度相关,因为learning_
rate 越低,就需要更多的树来构建具有相似复杂度的模型。随机森林的 n_estimators 值总是越大越好,但梯度提升不同,增n_estimators 会导致模型更加复杂,进而可能导致过拟合。通常的做法是根据时间和内存的预算选择合适的 n_estimators,然后对不同的learning_rate 进行遍历。另一个重要参数是 max_depth(或 max_leaf_nodes),用于降低每棵树的复杂度。梯度提升模型的 max_depth 通常都设置得很小,一般不超过 5。