1083 Windy数(数位dp)
1. 问题描述:
Windy 定义了一种 Windy 数:不含前导零且相邻两个数字之差至少为 2 的正整数被称为 Windy 数。Windy 想知道,在 A 和 B 之间,包括 A 和 B,总共有多少个 Windy 数?
输入格式
共一行,包含两个整数 A 和 B。
输出格式
输出一个整数,表示答案。
数据范围
1 ≤ A ≤ B ≤ 2 × 10 ^ 9
输入样例1:
1 10
输出样例1:
9
输入样例2:
25 50
输出样例2:
20
来源:https://www.acwing.com/problem/content/1085/
2. 思路分析:
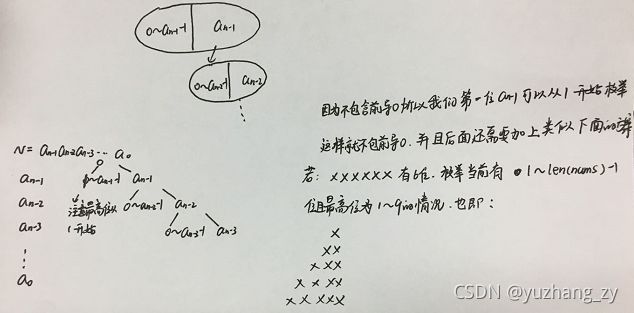
分析题目可以知道我们需要求解区间[a,b]满足不包含前导0并且相邻两个数字的差为2性质的数的个数,由这个特点可以知道这道题目属于数位dp的题目。对于数位dp的题目都是类似的套路,借助于树的形式来分析,具体的实现步骤如下:以区间的其中一个端点y为例,首先是需要预处理二维数组f,这样后面在枚举y的每一位的时候左边的分支可以直接计算出来(一般都是组合数),类似于1082 题数字游戏,当前的最高位只与次高位是有关系的,所以我们可以借助于1082题f数组的状态表示和状态计算的思路,定义一个二维数组f,其中f[i][j]表示最高位为j且总共为i位的Windy数的个数,怎么样递推呢?(状态计算),我们可以使用三层循环枚举,第一层循环枚举当前总共有i位,第二层循环枚举i位数字的最高位填j,第三层循环枚举次高位填k,只有当abs(j - k) >= 2说明才是合法的,这样我们通过预处理就将所有总共有i位最高位填k的情况计算出来了,预处理的目的是为了枚举左边分支填0~x-1的时候可以直接计算出对应的结果;预处理f数组之后,我们需要将区间端点y的每一位扣出来存储到nums中,然后逆序枚举nums中的每一位数字,对于当前的第i位数字x = nums[i],我们可以尝试填0~x-1,当第i位填0~x-1的时候就可以直接累加上之前预处理的结果了,进入到循环的下一位的时候表示第i位填x,当我们在枚举的时候发现不满足条件之后可以直接break,需要注意的是这道题目不包含前导0因为包含前导0之后可能会导致到不满足Windy数的要求,而在递推的时候是考虑了前导0的所有我们在枚举高位的时候一定要从1开始枚举,最后再考虑最高位为0的情况(隐含的0--例如首位填0那么下一位可以随便填而不用计算相邻两位的绝对值之差是否小于等于2)。这道题目的处理方式与1082题很像可以对比理解其中的解决过程。
3. 代码如下:
迭代写法:
from typing import List
class Solution:
# 与1082不降数的题目是类似的都是枚举最高位与次高位填的数字是什么
def init(self, N: int, f: List[List[int]]):
# 注意这里在枚举的时候需要计算到dp[i][0]的值, 如果不算会出现错误, 因为例如2位数字n = 20可以由dp[1][0]转移过来
for i in range(10): f[1][i] = 1
for i in range(2, N):
# 这里考虑了最高位为0的情况
for j in range(10):
for k in range(10):
if abs(j - k) >= 2:
f[i][j] += f[i - 1][k]
# 计算区间[0, n]的Windy数的个数, 这里将0算不算答案都没有影响, 因为做差之后结果0这个情况会抵消掉
def dp(self, n: int, f: List[List[int]]):
# 边界, 这里将0归为不是windy数
if n == 0: return 0
nums = list()
while n > 0:
nums.append(n % 10)
n //= 10
# last表示上一个填的数字只要与0~9的数字绝对值差值大于等于2即可
res, last = 0, -2
for i in range(len(nums) - 1, -1, -1):
x = nums[i]
# 判断是否是首位, 首位应该从1开始填, 否则可以填0, 枚举当前这一位填小于x的情况
for j in range(1 if i == len(nums) - 1 else 0, x):
if abs(j - last) >= 2:
res += f[i + 1][j]
if abs(last - x) >= 2:
# 当满足条件之后说明可以接着尝试填下一个数字
last = x
# 当前的x与上一位填的数字last不满足题目的要求, 说明这一位填x后面不管填什么的方案都是不满足题目要求了直接break
else:
break
# 最右边那个分支
if i == 0: res += 1
# 枚举之前没有计算的前导0的特殊情况, 只需要枚举到len(nums) - 1即可, 最高位上面已经累加到答案中了
for i in range(1, len(nums)):
# 当前有1~9位最高位为1~9的方案数目
for j in range(1, 10):
res += f[i][j]
return res
def process(self):
x, y = map(int, input().split())
N = 11
f = [[0] * 10 for i in range(N)]
self.init(N, f)
return self.dp(y, f) - self.dp(x - 1, f)
if __name__ == "__main__":
print(Solution().process())dfs:
下面补充一下数位dp的dfs写法,使用dfs写法相对于迭代式的数位dp写法的思维量和代码量都比较小,并且计算答案的速度与迭代式的数位dp都是差不多的,一般来说数位dp的dfs需要结合记忆化搜索实现(声明相应维度的数组来记录求解过的结果),如果不使用记忆化搜索来解决那么很容易就超时,其实使用dfs和迭代式的数位dp一样都是有固定的套路的,思考过程也是类似的,首先根据题目需要满足的性质确定dfs方法中需要传递哪些动态变化的参数,对于这道题目来说,需要传递的参数:当前还剩下k位要填的数字,可以理解为当前递归的位置,上一位填的数字是last(要求相邻两个数字之差的绝对值大于等于2所以需要记录上一个填的数字last),上一位填的数字是否达到了最大值lim,也即填的是x = nums[k - 1],使用这个标记是为了判断当前这一位可以填哪些数字,上一位是否是首位填0的标记isStart,记忆化搜索的本质其实就是根据这些动态变化的参数设置数组的维度来记录已经求解过的值,其实也很好理解如果我们之前求解过方法中一模一样的参数值,接下来的递归求解过程不就是重复求解了吗,也即与之前一模一样求解的过程,所以我们需要使用一个数组来记录递归过程中已经求解过的值;考虑到在递归的时候达到上限lim的次数是比较少的,所以只需要记录没有达到上限lim的方案数目到数组中即可,所以根据上面的考虑我们可以声明三维数组(其实省略掉了一维记录使用一个if判断来表示不是上限的lim的情况),其中f[i][j][k]表示还剩下i位要填的数字,上一位填的数字为j,首位是否填0的情况k,下面是使用三维数组f记忆化搜索的写法:
from typing import List
class Solution:
# lim表示是否达到上界也即上一位填的是否是最大值x = nums[k - 1], isStart表示当前是否是首位填数0的情况, 用来处理前导0的情况, 使用这个标记来特判掉首位填0的情况因为上一位是0那么下一位的数字其实是可以填任何数字的而不特判的情况下会筛选掉与0绝对值小于2的数字的情况所以答案会变少所以这里使用isStart来判断是否是首位填0的情况, last用来记录上一个数字
def dfs(self, k: int, last: int, lim: bool, isStart: int, nums: List[int], f: List[List[List[int]]]):
if k == 0: return 1
# 没有达到上限的情况下数组值大于等于0说明之前已经求解过了直接返回即可
if not lim and f[k][last][1 if isStart else 0] >= 0: return f[k][last][1 if isStart else 0]
res = 0
# 判断当前这一位可以填的最大数字
up = nums[k - 1] if lim == 1 else 9
for i in range(up + 1):
# 上一位与当前这一位填的绝对值之差需要大于等于2或者是上一位是首位并且填0的情况那么这一位可以填i
if abs(i - last) >= 2 or isStart:
res += self.dfs(k - 1, i, lim and i == up, isStart and i == 0, nums, f)
# 记忆化的过程, 只记录没有到达上限的情况, 判断的时候也是判断没有达到上限的情况, 记录与判断是是一一对应的
if not lim: f[k][last][1 if isStart else 0] = res
return res
# 数位dp的dfs写法其实与迭代式的写法的思考过程都是类似的, 都是考虑每一位填什么的情况, 每一次累加的是下一位到最后一位求解的方案数目那么最终得到的就是考虑每一位填什么的方案数目
def dp(self, n: int):
nums = list()
# 将n的每一位抠出来
while n > 0:
nums.append(n % 10)
n //= 10
# 初始化为-1之后才可以判断是否求解过当前的数组值
f = [[[-1] * 2 for i in range(10)] for j in range(11)]
return self.dfs(len(nums), -2, True, True, nums, f)
def process(self):
a, b = map(int, input().split())
return self.dp(b) - self.dp(a - 1)
if __name__ == "__main__":
print(Solution().process())补充一下四维数组的写法,这样就不用使用上面的if判断是否到达上限了,因为第四维就可以表示是否达到上限:
from typing import List
class Solution:
# 下面这个写法是根据根据dfs方法中动态变化的参数声明与之一一对应的思维数组f来记录的记忆化搜索方法
def dfs(self, k: int, last: int, lim: bool, isStart: int, nums: List[int], f: List[List[List[int]]]):
if k == 0: return 1
if f[k][last][1 if isStart else 0][1 if lim else 0] >= 0: return f[k][last][1 if isStart else 0][1 if lim else 0]
res = 0
up = nums[k - 1] if lim == 1 else 9
for i in range(up + 1):
if abs(i - last) >= 2 or isStart:
res += self.dfs(k - 1, i, lim and i == up, isStart and i == 0, nums, f)
f[k][last][1 if isStart else 0][1 if lim == 1 else 0] = res
return res
def dp(self, n: int):
nums = list()
while n > 0:
nums.append(n % 10)
n //= 10
f = [[[[-1] * 2 for i in range(2)] for j in range(10)] for k in range(11)]
return self.dfs(len(nums), -2, True, True, nums, f)
def process(self):
a, b = map(int, input().split())
return self.dp(b) - self.dp(a - 1)
if __name__ == "__main__":
print(Solution().process())