基于skimage的数字图像处理——频域滤波（傅里叶变换）

注意：文章代码基于notebook实现，也可修改后用于pycharm等编译器。

---

前言

本次学习的大致内容：

频域滤波的概念；
傅里叶变换在图像处理中的应用意义；
通过python编程实现对图像的简单傅里叶变换，并显示其频谱图。

---

代码大多基于skimage实现，所以先在notebook或pycharm中下载安装skimage。
在notebook中执行代码：!pip install scikit-image即可实现skimage的安装

---

一、频域滤波与傅里叶变换

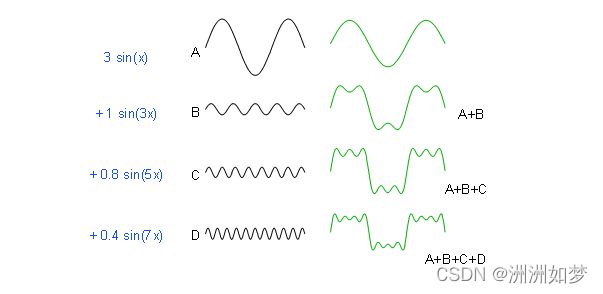
著名的法国数学家傅里叶在其著作《热分析理论》中指出：任何周期函数都可以分解为不同频率的正弦或余弦级数的形式，即傅里叶级数。

傅里叶变换从本质上完成了空间信息到频域信息的变换，通过变换将空域信号处理问题转化为频域信号处理。

二、skimage代码实现

1.简单的傅里叶变换：

代码如下：

# 初始化，导入绘图库及工具包
import numpy as np
import matplotlib.pyplot as plt
x=np.arange(0,4*np.pi,0.01)

plt.figure(figsize=(12,16))  # 规定整体图像的大小

plt.subplot(421)    # 输出图像分块显示，该图为四行两列中的第一张图像
y=np.sin(x)*3
plt.plot(x,y)
plt.title('A')

plt.subplot(422)
y1=np.sin(3*x)
plt.plot(x,y1)
plt.title('B')

plt.subplot(423)
y2=np.sin(x)*3+np.sin(3*x)
plt.plot(x,y2)
plt.title('A+B')

plt.subplot(424)
y3=np.sin(5*x)*0.8
plt.plot(x,y3)
plt.title('C')

plt.subplot(425)
y3_2=3*np.sin(x)+np.sin(3*x)+np.sin(5*x)*0.8
plt.plot(x,y3_2)
plt.title('A+B+C')

plt.subplot(426)
y4=np.sin(7*x)*0.4
plt.plot(x,y4)
plt.title('D')

plt.subplot(427)
y4_1=3*np.sin(x)+np.sin(3*x)+np.sin(5*x)*0.8+np.sin(7*x)*0.4
plt.plot(x,y4_1)
plt.title('A+B+C+D')

plt.show()

结果显示如下：

2.不同种类的正弦波及其傅里叶变换频谱图

代码如下：

import numpy as np
import matplotlib.pyplot as plt

#导入字体库
from matplotlib.font_manager import FontProperties
# 此处笔者没有提供simhei.ttf文件，该文件为自行导入的文件
font = FontProperties(fname='simhei.ttf', size=13)    # 创建字体对象，设置字体大小
plt.rcParams['axes.unicode_minus'] = False      #字符显示

def show(ori_func, ft, sampling_period = 5):
    n = len(ori_func)
    interval = sampling_period / n

    # 绘制原始函数
    plt.figure(figsize=(16,8))
    plt.subplot(221)
    plt.plot(np.arange(0, sampling_period, interval), ori_func, 'black')
    plt.xlabel('时间/s',fontproperties=font)
    plt.ylabel('振幅',fontproperties=font)
    plt.title('原始信号',fontproperties=font)

    # 绘制变换后的函数
    plt.subplot(222)
    frequency = np.arange(n/2) / (n*interval)
    nfft = abs(ft[range(int(n/2))]/n)
    plt.plot(frequency, nfft, 'red')
    plt.xlabel('频率/Hz',fontproperties=font)
    plt.ylabel('频谱',fontproperties=font)
    plt.title('傅里叶变换结果',fontproperties=font)
    plt.show()

# 单一正弦波傅里叶变换
time = np.arange(0, 5, .005)
x = np.sin(2 * np.pi * 1 * time)   # 生成频率为1的正弦波
y = np.fft.fft(x)    # 对其进行傅里叶变换
show(x,y)

# 对三个正弦波进行叠加，然后进行傅里叶变换
x2 = np.sin(2 * np.pi * 20 * time)   
x3 = np.sin(2 * np.pi * 60 * time)
x += x2 + x3         # 将上面频率为1的正弦波与频率为20和60的正弦波叠加起来
y = np.fft.fft(x)    # 将叠加后的结果进行傅里叶变换
show(x,y)

# 进行方波的傅里叶变换
# 生成方波，振幅是1，频率为10Hz
# 由于间隔是0.05s，每秒有200个点，所以需要每隔20个点设为1
x = np.zeros(len(time))
x[::20] = 1
y = np.fft.fft(x)
show(x,y)

# 进行脉冲波的傅里叶变换
x = np.zeros(len(time))
x[380:400] = np.arange(0, 1, .05)
x[400:420] = np.arange(1, 0, -.05)
y = np.fft.fft(x)
show(x,y)

结果显示如下：
单一正弦波及其傅里叶变换结果：

3个正弦波叠加波形及其傅里叶变换结果：

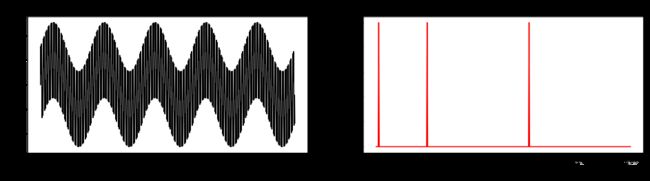
方波及其傅里叶变换结果：

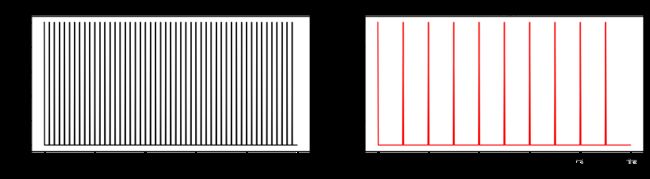
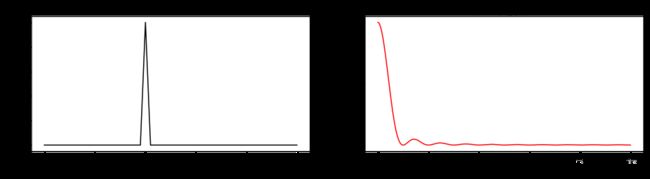
脉冲波及其傅里叶变换结果：

3.二维傅里叶变换

在一维傅里叶变换上进行简单扩展。
代码如下：

from skimage import data
import numpy as np 
from matplotlib import pyplot as plt 

# 导入字体库
from matplotlib.font_manager import FontProperties
font = FontProperties(fname='simhei.ttf', size = 14)    #创建字体对象，设置字体大小
plt.rcParams['axes.unicode_minus'] = False    #字符显示

# 导入测试图片
img = data.camera()
f = np.fft.fft2(img)    # 快速傅里叶变换算法得到频率分布
fshift = np.fft.fftshift(f)    # 默认结果中心点位置是左上角，将其转移到中间位置
fimg = np.log(np.abs(fshift))  # fft结果是复数，求其绝对值之后才是振幅

# 展示结果
plt.figure(figsize=(10,10))
plt.subplot(121)
plt.imshow(img, 'gray')
plt.title('原始图像', FontProperties = font)

plt.subplot(122)
plt.imshow(fimg, 'gray')
plt.title('傅里叶变换图像', FontProperties = font)

plt.show()

结果显示如下：

4.二维傅里叶变换的性质

①可分离性

二维离散傅里叶变换可视为由沿x，y方向的两个一维傅里叶变换所构成。

代码如下：

from skimage import io, transform, data, color
import numpy as np 
from matplotlib import pyplot as plt 

# 导入字体库
from matplotlib.font_manager import FontProperties
# 创建字体对象，设置字体大小
font = FontProperties(fname = 'simhei.ttf', size = 16)
plt.rcParams['axes.unicode_minus'] = False    #显示字符

# 导入图像
img = data.coffee()
img1=img
img=color.rgb2gray(img)

#在x方向实现傅里叶变换
m,n=img.shape
fx=img
for x in range(n):
    fx[:,x]=np.fft.fft(img[:,x])
for y in range(m):
    fx[y,:]=np.fft.fft(img[y,:])
fshift = np.fft.fftshift(fx)     # 默认结果中心点位置是在左上角，转移到中间位置
fimg = np.log(np.abs(fshift))    # fft 结果是复数，求绝对值结果才是振幅

# 展示结果
plt.subplot(121)
plt.imshow(img1, 'gray')
plt.title('原图像',fontproperties=font)
plt.subplot(122)
plt.imshow(fimg, 'gray')
plt.title('傅里叶变换图像',fontproperties=font)
plt.show()

结果显示如下：
（使用两次一维傅里叶变换代替二维傅里叶变换的结果）

②旋转特性

图像旋转一定角度之后，频谱图像也会得到相应旋转。

根据下面的提示和要求，完成图像的旋转特性的效果展示：
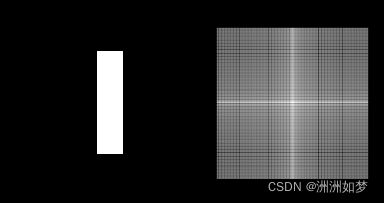
（1）利用函数（np.zero) 生成一个600* 600的单通道图像，并在该图中心生成一个高400宽40的白色矩形；
（2）实现上步中图像的傅里叶变换，并显示其频谱图；
（3）利用旋转函数把第一张图像顺时针旋转45度；
（4）实现旋转后图像的傅里叶变换，并显示其频谱图。

代码如下：

# 初始化，导入包
from skimage import io, transform, data, color
import numpy as np 
from matplotlib import pyplot as plt 

# 导入字体库
from matplotlib.font_manager import FontProperties
# 创建字体对象，设置字体大小
font = FontProperties(fname = 'simhei.ttf', size = 16)
plt.rcParams['axes.unicode_minus'] = False    #显示字符

# 利用函数（np.zero)生成一个600* 600的单通道图像，并在该图中心生成一个高400宽100的白色矩形
image=np.zeros((600,600),dtype='uint8')
for i in range(100,501):
    for j in range(250,351):
        image[i,j]=255
f=np.fft.fft2(image)
fshift = np.fft.fftshift(f)     # 默认结果中心点位置是在左上角，转移到中间位置
fimg = np.log(np.abs(fshift))   # fft 结果是复数，求绝对值结果才是振幅
# 展示结果
plt.figure(figsize=(6,8))
plt.subplot(121)
plt.imshow(image, 'gray')
plt.title('单通道图像',fontproperties=font)
plt.subplot(122)
plt.imshow(fimg, 'gray')
plt.title('傅里叶变换图像',fontproperties=font)
plt.show()

image2 =transform.rotate(image,-45) 
f=np.fft.fft2(image2)
fshift = np.fft.fftshift(f) # 默认结果中心点位置是在左上角，转移到中间位置
fimg = np.log(np.abs(fshift)) # fft 结果是复数，求绝对值结果才是振幅
# 展示结果
plt.figure(figsize=(6,8))
plt.subplot(121)
plt.imshow(image2, 'gray')
plt.title('旋转图像',fontproperties=font)
plt.subplot(122)
plt.imshow(fimg, 'gray')
plt.title('傅里叶变换图像',fontproperties=font)
plt.show()

结果显示如下：

---

总结

以上就是今天要讲的内容，本文简单介绍了图像傅里叶变换基于skimage的代码实现，小伙伴们也可以自行探索，欢迎讨论。