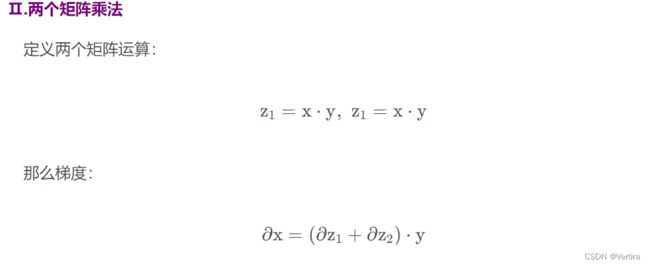paddle 中的backward（）函数

对！ 你没有看错，就是这个：

paddle.autograd.backward(tensors, grad_tensors=None, retain_graph=False)

官方注解：

计算给定的 Tensors 的反向梯度。（问题1，它这个梯度是怎么计算的？，先不管） 

参数¶

• tensors (list[Tensor]) – 将要计算梯度的Tensors列表。 Tensors中不能包含有相同的Tensor。

• grad_tensors (None|list[Tensor|None], 可选) – tensors 的初始梯度值。如果非None, 必须和 tensors 有相同的长度， 并且如果其中某一Tensor元素为None，则该初始梯度值为填充1.0 的默认值；如果是None，所有的 tensors 的初始梯度值为填充1.0 的默认值。默认值：None。

• retain_graph (bool，可选) – 如果为False，反向计算图将被释放。如果在backward()之后继续添加OP， 需要设置为True，此时之前的反向计算图会保留。将其设置为False会更加节省内存。默认值：False。

返回¶

None

 官方实例：

import paddle
x = paddle.to_tensor([[1, 2], [3, 4]], dtype='float32', stop_gradient=False)
y = paddle.to_tensor([[3, 2], [3, 4]], dtype='float32')

grad_tensor1 = paddle.to_tensor([[1,2], [2, 3]], dtype='float32')
grad_tensor2 = paddle.to_tensor([[1,1], [1, 1]], dtype='float32')

z1 = paddle.matmul(x, y)
z2 = paddle.matmul(x, y)

paddle.autograd.backward([z1, z2], [grad_tensor1, grad_tensor2], True)
print(x.grad)
#[[12. 18.]
# [17. 25.]]

x.clear_grad()

paddle.autograd.backward([z1, z2], [grad_tensor1, None], True)
print(x.grad)
#[[12. 18.]
# [17. 25.]]

x.clear_grad()

paddle.autograd.backward([z1, z2])
print(x.grad)
#[[10. 14.]
# [10. 14.]]

 只看程序，没有报错，但是不知道这结果是怎么算出来的。

这里将一下求导，矩阵的求导（可以参考  矩阵论，高等数学二元函数求导）

 如果要求x的梯度，先求z的梯度，z的梯度在反馈中，就是这个paddle.autograd.backward（）中，如果这里面默认为none呢，上面官方已经数的很清楚，初始梯度1.0。

官方总归是官方，不实际测试一下，心里不踏实。简单实例测试一下

import paddle
# 下面用命令行执行了，测试
>>> x = paddle.to_tensor([1], dtype='float32', stop_gradient=False)
>>> y = paddle.to_tensor([2], dtype='float32')
>>> z = paddle.matmul(x, y)
>>> print("x: {}".format(x),"y: {}".format(y),"z: {}".format(z))
# 输出情况如下，
x: Tensor(shape=[1], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [1.]) 
y: Tensor(shape=[1], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [2.]) 
z: Tensor(shape=[1], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [2.])

# .在backward之前  看看它们的梯度什么情况 

>>> print("x.grad: {}".format(x.grad), "y.grad: {}".format(y.grad), "z.grad: {}".format(z.grad))
# 输出结果
x.grad: None y.grad: None z.grad: None

 全部都是None，不使用backward，这梯度不存在的

# 先调用backward
>>> paddle.autograd.backward(z, paddle.to_tensor([3], dtype='float32'))
# 再打印他们的梯度
>>> print("x.grad: {}".format(x.grad), "y.grad: {}".format(y.grad), "z.grad: {}".format(z.grad))
#结果如下

x.grad: Tensor(shape=[1], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [6.]) 
y.grad: None 
z.grad: Tensor(shape=[1], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [3.])
>>>

大家看到他们的梯度了吧，z.grad （提前设置好的初值，你也可以设置为None,试一试效果）和y矩阵就可以计算出x.grad，自己可以动手算一算

 推算的结果与 上面输出的结果一样，都是6

这里backword 不能重复调用计算，容易出错，

RuntimeError: (Unavailable) auto_0_ trying to backward through the same graph a second time, but this graph have already been freed. Please specify Tensor.backward(retain_graph=True) when calling backward at the first time.
  [Hint: Expected var->GradVarBase()->GraphIsFreed() == false, but received var->GradVarBase()->GraphIsFreed():1 != false:0.] (at /paddle/paddle/fluid/imperative/basic_engine.cc:74)

即使调用 clear_grad()，也无法保证重新计算backward()

x.clear_grad()
y.clear_grad()
z.clear_grad()

将autograd.backward函数中的retain_graph设置为TRUE。

paddle.autograd.backward(z, TT([3], dtype='float32'), retain_graph=True)

 此时就可以重复调用backward。

print("x.grad: {}".format(x.grad), "y.grad: {}".format(y.grad), "z.grad: {}".format(z.grad))

x.grad: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,
       [6.])
y.grad: None
z.grad: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,
       [3.])

第二次调用则

x.grad: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,
       [12.])
y.grad: None
z.grad: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,
       [3.])

实例二（接着上面的，我就不重复调用paddle包了）

>>> x = paddle.to_tensor([[1,2],[3,4]], dtype='float32', stop_gradient=False)
>>> y = paddle.to_tensor([[3,2],[3,4]], dtype='float32')
>>> z = paddle.matmul(x, y)
# 打印x,y,z的结果，可以手动计算一下z，看看和计算机计算的是否一样
>>> print("x: {}".format(x),"y: {}".format(y),"z: {}".format(z))
x: Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[1., 2.],
        [3., 4.]]) y: Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[3., 2.],
        [3., 4.]]) z: Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[9. , 10.],
        [21., 22.]])
# 下面调用了 backward
>>> paddle.autograd.backward(z, paddle.to_tensor([[1,2],[2,3]], dtype='float32'), retain_graph=True)
# 然后打印 x，y，z的梯度，z的初始梯度已经在上面初始化好了
>>> print("x.grad: {}".format(x.grad), "y.grad: {}".format(y.grad), "z.grad: {}".format(z.grad))
x.grad: Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[7. , 11.],
        [12., 18.]]) 
y.grad: None 
z.grad: Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[1., 2.],
        [2., 3.]])

从中可以看到，对于矩阵的自动反向梯度，所遵循的与标量基本是一样的。

>>> print("y*z.grad: {}".format(y.numpy().dot(z.grad.numpy())))
y*z.grad: [[ 7. 12.]
 [11. 18.]]
>>>

>>> x = paddle.to_tensor([[1,2],[3,4]], dtype='float32', stop_gradient=False)
>>> y = paddle.to_tensor([[3,2],[3,4]], dtype='float32')
>>> z1 = paddle.matmul(x, y)
>>> z2 = paddle.matmul(x, y)
>>> print("x: {}".format(x),"y: {}".format(y),"z: {}".format(z))
# 输出x，y，z的值
x: Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[1., 2.],
        [3., 4.]]) 
y: Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[3., 2.],
        [3., 4.]]) 
z: Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[9. , 10.],
        [21., 22.]])
#调用backward
>>> paddle.autograd.backward(z1, paddle.to_tensor([[1,2],[2,3]], dtype='float32'))
>>> paddle.autograd.backward(z2, paddle.to_tensor([[1,1],[1,1]], dtype='float32'))
#输出结果命令
>>> print("x.grad: {}".format(x.grad), "y.grad: {}".format(y.grad), "z.grad: {}".format(z.grad))
# 结果如下
x.grad: Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[12., 18.],
        [17., 25.]]) 
y.grad: None 
z.grad: Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[1., 2.],
        [2., 3.]])
>>>

检验x的梯度矩阵：

# 首先要 import numpy as np,避免报错

print("y*(z1+z2).grad: {}".format(y.numpy().dot((z1.grad+z2.grad).numpy())))



输出结果
>>> print("y*(z1+z2).grad: {}".format(y.numpy().dot((z1.grad+z2.grad).numpy())))
# 结果如下
y*(z1+z2).grad: [[12. 17.]
 [18. 25.]]
>>>

欢迎点赞收藏加关注

(18条消息) paddle中的自动求解梯度 ： autograd.backward_卓晴的博客-CSDN博客