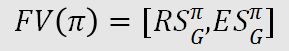最优理论与技术--多目标规划问题

目标规划的产生：

线性规划的局限性—— 目标单一性，不能处理多目标问题。但现在很多问题都有多个目标，希望能获得综合的最优，但目标之间往往存在一定的矛盾，如利润最高、成本最低、产量高、质量好、用工最少等。传统的线性规划很难同时处理？对于这种多目标的问题，如何解决？目标规划可统筹兼顾的处理多种目标的关系。

•三个目标要求，如何得到集中体现？

• 是否需要建立三个目标函数？

• 传统线性规划一般只建立一个目标函数，而有多个约束。→是否可以将三个目标以约束的形式表现出来，这样可解决多目标的问题？

相关概念引入：① 正、负偏差变量

  d+：正偏差量，可能实现值高于目标指标值的部分；

  d-：负偏差量，可能实现值低于目标指标值的部分。

实现目标的三种情况：( d+ * d—＝0  )

（1） 超过目标值          ｄk＋ >0 ，ｄk-- ＝0

 （2） 达不到目标值     ｄk＋ =0，ｄk-- >0

（3） 刚好达到目标值  ｄk＋ =0，ｄk-- ＝0

② 目标规划的约束形式

（1）绝对约束：也叫客观条件约束、硬约束，为必须严格满足的约束。

（2）目标约束：目标规划特有的约束，也叫软约束。

（3）非负约束：要求所有决策变量和偏差量均≥0。

• 约束一般包括目标约束、绝对约束和非负约束三部分；

• 目标函数转换成求多个期望目标值的偏差量和的最小；

• 目标及约束仍然为线性。

 目标规划所得的是满意方案。

•目标要求中，是否都需要同时满足？即实际中可能会出现需要某种情况越大越好（如利润），即在原有基本目标值的基础上偏离越大越好，也可能需要出现在原基本目标值的基础上越小越好（如成本）。  →这样的情况如何在目标函数中得到体现？

目标要求有轻重缓急的情况，这种情况如何在目标函数中体现？比如，要求必须优先保证产品质量，然后是控制成本，最后是达到产量要求？→优先量必须优先考虑，那如何率先满足优先目标？

目标有轻重缓急的情况，这种情况如何在目标函数中体现？比如，要求必须优先保证产品质量，然后是控制成本，最后是达到产量要求？→优先量必须优先考虑，那如何率先满足优先目标？越优先，代表目标函数中最先接近于0，则目标系数应越大。

采用优先权来区分目标的优先级别，并将其在目标函数中作为相应偏差量的目标系数。同时，根据优先级别不一样，应将目标系数拉开。

要求制订一生产计划，使其尽可能达到以下三项指标：

（1）满足需要量；合同型目标

（2）质量水平超过98%；利润型目标

（3）不超过7000元的工时成本。成本型目标

分成三种目标形式：

 （1）对于利润型目标，要求是可能实现值超过目标值越多越好，即d+越大越好，则在目标函数中，不能对d+求最小；

（2）对于成本型目标，要求可能实现值低于目标值越多越好，即d-越大越好，则在目标函数中不能对d-求最小；

（3）对于合同型目标，要求跟目标保持一致，不超过也不短缺，即要求d+和d-都最小，则在目标函数中应将两者综合考虑

目标函数的处理：

(1) 恰好达到目标（合同型目标）：

                 min Z= p(d k-+dk+)

(2) 超过目标（利润型目标）：

                 min Z= p (dk -)

(3) 不超过目标（成本型目标）：

                 min Z= p (dk+)

目标规划的一般数学模型：

建模方法：

               (1) 设定约束条件 (构建目标约束、绝对约束和非负约束)；

               (2) 规定目标约束优先级；

               (3) 根据目标所属的类型，建立新的目标函数，完成模型的建立。

推荐一篇机器之心解读关于多目标优化最新文章：“Wuji: Automatic Online Combat Game Testing Using Evolutionary Deep Reinforcement Learning 获顶会最佳论文，天津大学等用强化学习寻找游戏bug”。该论文主要融合了进化算法与深度强化学习算法，从多目标优化的角度，旨在解决大规模商业游戏的自动化智能测试问题，并荣获 ASE 2019 的最佳论文奖 (Distinguished Paper Award)。论文链接: https://yanzzzzz.github.io/files/PID6139619.pdf

 

背景介绍

 

长久以来，游戏测试一直被认为是一项极具挑战性的任务。在工业界，游戏测试一般使用脚本测试以及手动测试相结合的形式。时至今日，自动化游戏测试的研究仍然处于初级阶段，一个主要原因是玩游戏本身是一个持续决策的过程，而游戏缺陷（bug）往往隐藏的较深，只有当某些困难的中间任务完成后，才有可能被触发，这就要求游戏测试算法拥有类人的智能。近年来，深度强化学习算法（DRL）取得的非凡的成功，特别在游戏控制领域，甚至表现出了超越人类的智能，这为推进自动化游戏测试提供了启示。然而，既有的 DRL 算法主要关注如何赢得游戏，而不是游戏测试，导致其可能无法广泛地覆盖需要测试的分支场景。

 

为此，首选我们针对四款网易游戏产品中的 1349 个真实 bug 进行深入分析，并针对性的提出了四个用于 bug 检测的 oracle。其次，我们提出了实时游戏测试框架 Wuji，通过融合了进化算法，DRL 算法和多目标优化机制，实现了智能的自动化游戏测试。Wuji 在赢得游戏和探索游戏空间之间取得了较好的平衡。其中，赢得游戏可以使得智能体在游戏中取得进展；而空间探索则可以增加发现错误的可能性。

 

最后，我们使用一个仿真游戏和两个大型商业游戏对 Wuji 算法的效果进行了大规模评估，结果证明了 Wuji 在探索游戏状态空间方面以及检测 bug 方面的有效性。此外，Wuji 算法还检测到了游戏中先前从未被发现过的漏洞，进一步论证了算法的有效性。

 

 

Wuji - 基于多目标优化的进化强化学习框架

 

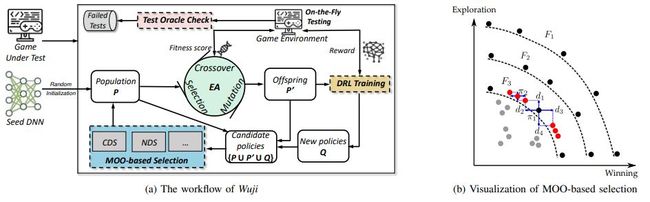
从强化学习算法的角度看，不同的策略π都能够探测到游戏中不同的状态空间。从进化算法的角度看，通过维护一个策略种群，可以实现游戏空间的高效探索。直观上，可以将二者结合，实现有效的游戏测试。Wuji 正是构建在这样的进化强化学习架构之上（上图）。

 

然而，进化算法需要选择优质的后代，而如前文所述，使用胜率作为策略的单一衡量指标，会使得种群内的策略都趋同于取胜，无法探测到更广泛的游戏空间，降低游戏测试效果。为此，Wuji 使用多目标优化机制，对每个策略分别从胜率以及空间探索能力两个维度衡量策略性能，并以此进行优质后代的选择。

 

具体来说，每个策略用于后代选择的 Fitness-Value (FV) 计算方式如下：

 

 

比如，给定游戏 G，使用策略π执行一个回合后，〖RS〗_G^π表示策略在当前回合的胜率，而〖ES〗_G^π表示策略π在当前回合中探索的状态空间的数量。至此，策略的 FV 从标量拓展到了向量。因此，后代选择的方式也从选择较大的标量，转变成了向量之间的比较。因此，本文提出使用非支配排序（non-dominate sorting, NDS）来选择非支配集（non- dominate set），进而选择更优质的后代。具体过程如上图（右）所示，图中每一个点代表一个策略，两个维度衡量了策略在获胜能力与探索能力两个维度的表现。其中，整个种群中存在一个集合 F_1，该集合中的策略相互不支配 (例如π_1 的胜利比π_2 高，但是探索能力却比较低；因此无法说明两个策略谁更优秀)，该策略集又被称为帕累托前沿 (Pareto Frontier)。

 

基于此，进行后代选择的时候，优先选择集合中的帕累托前沿（如 F_1）；接着从种群中剔除 F_1 后再进行非支配集的筛选，找到 F_2 在加入到后代中，循环往复直至种群数量达到上限。值得注意的是，当将 F_3 加入到后代种群时，如果遇到种群规模超出上限阈值的情况，需要针对 F_3 内的策略进行筛选。

 

为此，本项目提出使用聚集距离（crowding distance）对策略的密集程度进行度量，并基于聚集距离实现策略的聚集距离排序算法（crowding distance sorting, CDS）实现策略的末位淘汰。如上图右所示，针对策略π_1，其聚集距离定义如下公式：

 

 

其中 d_1 与 d_4 衡量了在探索能力的维度，距离π_1 最近的邻居策略的距离。同理，d_2 与 d_3 衡量了胜率维度的距离。根据聚集距离对策略进行 CDS，保留聚集距离较大的策略，淘汰聚集距离较小的策略，以此实现策略的多样性。CDS 尽可能选择两端的策略，以及均匀分布在两个极端之间的策略，以实现后代策略的多样性。

 

综上所述，Wuji 借助进化强化学习算法框架，结合多目标优化机制，使得种群内的策略朝着胜率以及探索能力两个方向不断优化，同时还保证部分策略均匀的分布在两个优化目标之间。二者的融合使 Wuji 能够完成更多任务并探索游戏的更多状态，提升发现 bug 的几率。

 

实验结果

 

 

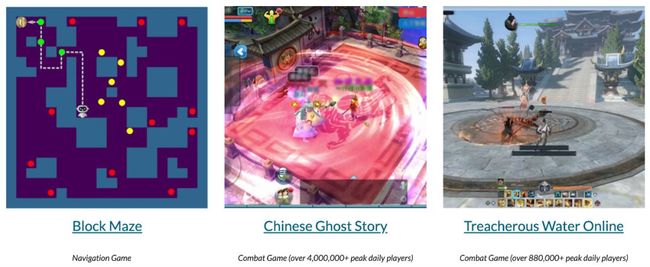
我们在仿真迷宫环境 (Block Maze) 和网易游戏《倩女幽魂》（L10）与《逆水寒》(NSH) 上分别进行了实验，实验结果证明了 Wuji 在探索游戏状态空间方面以及检测 bug 方面的有效性，还发现了先未知的漏洞。

 

 

在仿真迷宫环境中，我们注入了随机分布的 bugL10 以及 NSH 分别注入了游戏开发过程中真实发现的 bug。在此基础上，我们分别使用了猴子测试算法（Random）、基于单目标优化的进化算法（EA_S）、基于多目标优化的进化算法（EA_M）、深度强化学习算法（DRL, aka. A3C）、进化强化学习算法（EA_S+DRL）以及 Wuji 算法对三个游戏环境进行了测试，并记录下测试过程发现的 bug，结果如上图 5 所示（平均发现的 bug 数量）。

 

总体来说，Wuji 相比其他算法发现了更多的漏洞；同时，上图 6 展示了不同算法最终发现 bug 的数量的箱形统计图，进一步论证了 Wuji 算法发现更多 bug 这一结论的统计意义。

 

 

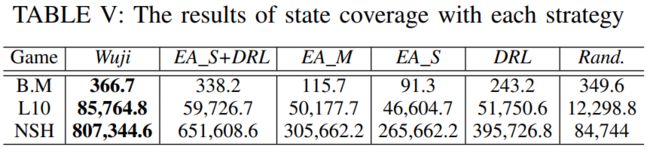
另一方面，上表统计了不同算法在游戏测试过程中的状态空间的覆盖情况（去重后的状态数量）。可以发现，Wuji 相比其他算法在同样的设备与测试时间下，探索到了更多的状态空间，这也进一步解释了 Wuji 能够发现更多 bug 的原因。

 

最后值得一提的发现是，在传统系统测试中，代码覆盖率是衡量系统测试完备性的一个重要指标；但在整个测试过程中，6 个相关算法的代码覆盖率基本一致，而通过上述实验结论，我们认为使用状态空间覆盖数量作为衡量游戏软件的测试完备性指标，具有较高的有效性；且从强化学习的角度来看，该指标也具有较强的逻辑性与解释性。

 

本文是深度强化学习研究在游戏测试领域的初步探索，且该领域还存在诸多难题以及值得研究的方向。本课题组会沿着该方向，致力于推动深度强化学习技术在智能游戏测试产业的落地与发展。