多种群协同差分进化多目标优化

多种群协同差分进化多目标优化
摘要
提出了一种用于多目标优化的多种群协同差分进化算法。对于一个M目标优化问题，该算法有M个单目标优化子种群和一个存档种群。将自适应DE应用于每个子种群，以优化多目标优化问题（MOP）的相应目标。存档填充还通过自适应DE进行优化。存档填充不仅用于维护迄今为止发现的所有非主导解决方案，还用于指导每个子填充沿整个Pareto前沿搜索。这些（M+1）人群通过使用自适应DE合作优化MOP的所有目标。对具有两个、三个和多个目标的基准问题的仿真结果表明，该算法优于一些最新的多目标DE算法和其他流行的多目标进化算法。研究了该算法的在线搜索行为和参数敏感性。

介绍
许多现实世界的问题都可以表示为多目标优化问题（MOP），因为它们自然有两个或多个必须同时优化的冲突目标。这些现实问题存在于各个领域[1]。进化算法（EA）特别适用于求解MOP，并且已经很流行，因为它们可以在一次运行中获得一组可能的解，而不是像传统优化技术那样在一系列单独运行中获得。此外，EA对Pareto（PF）的形状或连续性不太敏感，它们可以轻松处理不连续和凹形PF。
最流行的MOEA是非主导排序算法II（NSGA-II）[2]和基于分解的MOEA（MOEA/D）[3]。更多关于MOEA开发和应用的研究可以在评论中找到

差异进化（DE）[6]是一种简单而强大的基于群体的EA。DE的优点是易于使用、结构简单、有效性和鲁棒性。DE具有良好的优化能力，已成功应用于各种科学和工程领域的许多单目标优化问题。自然，作为一种单目标优化算法，其相对简单和成功促使研究人员将DE的应用扩展到MOP。自从Abbass等人[7]首次探索DE对MOP的潜力以来，在[8]-[11]中提出了几个多目标DE（MODE）。由于NSGA-II和MOEA/D是两种流行的MOEA框架，大多数MODE[8]、[10]都基于这些框架（见第II-B节）。

本文提出了一种协作多目标DE（CMODE），它受到协同进化多种群粒子群优化（CMPSO）的启发[12]。CMODE使用多个群体来处理多个目标，而不是用传统的基于帕累托的方法将同一群体作为一个整体来处理所有目标。每个群体只处理一个目标，所有群体合作以接近整个PF。对具有两个、三个和多个目标的基准问题的仿真结果表明，CMODE优于一些最先进的MODE和其他流行的MOEA。

本文的主要贡献有两方面。1） 本文介绍了MODE的新版本。CMODE有几个优点。它非常简单，并利用具有自适应参数的先进单目标DE进行多目标优化。CMODE可以看作是一个并行的MOEA，它不仅可以解决两个和三个目标问题，还可以解决许多目标问题。2） 本文全面比较了CMODE与流行的基于Pareto和基于分解的MODE或MOEA
本文的其余部分组织如下。第二节回顾了DE和MODE的相关工作。CMODE见第三节。实验结果见第四节。最后，结论见第五节。

背景
对于单目标优化问题
最小化f（X）

DE使用D维参数向量演化NP候选个体（解）群体[6]。

每个个体表示为

其中i=1，2，…，NP，NP是种群大小，G是当前世代。
它有三个主要算子：1）突变；2） 交叉；和3）选择。
1） 突变：该算子针对每个个体Xi，G（称为目标向量）生成突变向量Vi，G。几种常用的突变策略如下[6]、[13]、[14]。

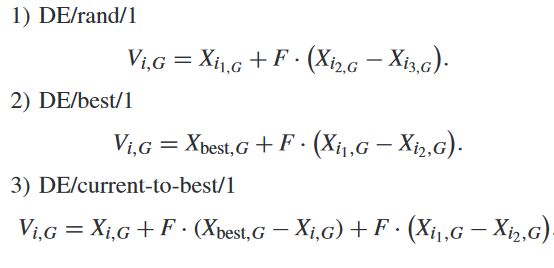
索引i1–i3是从集合{1，2，…，NP}{i}中选择的相互不同的随机索引。Xbest，G是第G代的最佳矢量。F是正突变比例因子。

交叉：该算子应用于每对目标向量X(i，j，G)和突变向量V(i、j、G)，
以生成试验向量Ui，G=[Ui，1，G，Ui，2，G，…，Ui，D，G]。

有两种交叉算子，二项式和指数型。最广泛使用的是二项式交叉，如下所示：

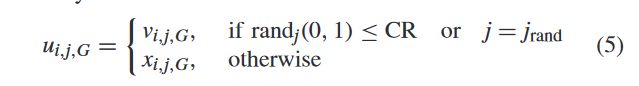
其中，randj（0，1）是j维CR的[0,1]中的均匀随机数∈ [0,1]是预定义的交叉控制参数，jrand∈ [1，D]是从1到D中随机选择的整数。
3） 选择：该算子使用一对一的贪婪方案，在目标向量Xi，G和试验向量Ui，G之间选择更好的一个，以便在下一代中生存，如下所示：

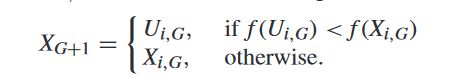
DE并非完全没有停滞和过早收敛的问题[13]，[14]。因此，提出了许多DE变体[13]、[14]。
对这些DE变体的修改主要集中在控制参数（即NP、F和CR）[15]-[17]、运算符（变异、交叉和选择）[18]、[19]、种群（多种群或并行种群）[20]，以及DE与其他运算符或算法的杂交[21]。
在这些高级DE中，JADE[16]和jDE[17]是两个简单且流行的自适应DE。它们在第三节中进行了调整，以分别优化CMODE的单目标子种群和归档种群。

MODE相关工作
具有多个种群的现有MOEA

MOP的CMODE

动机和总体框架
本文的动机来自以下两个方面。一方面，已经提出了许多用于单目标优化的强大高级DE变体。通过扩展先进的单目标DE，提出新版本的MODE具有重要意义。
另一方面，尽管VEGA是第一个MOEA，但与流行的NSGA-II和MOEA/D相比，这种向量评估方法尚未得到广泛研究。CMPSO[12]作为一种最新的矢量评估方法，获得了比VEPSO和最流行的MOEA更好的性能。这促使我们进一步挖掘该方法的潜力。因此，本文利用合作种群和现有的先进单目标DE，提出了一种新的模式。

图1显示了CMODE的人口结构和主要组成部分。对于M目标优化问题，CMODE有M个单目标优化子种群和一个存档种群。
每个单目标子群体用于优化MOP的相应目标。存档搜索还应进一步改善存档人口。
存档总体不仅用于维护迄今为止所有总体找到的所有非主导解决方案，还用于指导每个单目标子总体沿整个PF搜索。这些（M+1）人群合作优化MOP的所有目标。
存档的重要性

更具体地说，在每一代中，第m个子种群中个体的适应值由MOP的第m目标函数指定。因此，个体不会被不同的冲突目标所迷惑，可以根据相应的目标/方向来搜索PF的不同区域。然而，由于每个子群体只专注于优化一个目标/方向，因此每子群体中的个体可能会被引导到相应目标/方向的边缘或极点，从而导致整个PF的低效近似。
为了解决这个问题，不同的单目标亚群共享他们的搜索信息，并通过存档人口在某种程度上接近整个PF。
此外，还可以优化归档人口本身，使其接近整个PF。因此，用于集中搜索的每个子种群和用于全局搜索的存档种群合作以近似于整个PF
图1中突出显示了三个主要组成部分，如单目标子种群的DE、档案种群DE和档案更新方案，如下所示。

单目标子群体的DE
对于第m个单目标子种群群，采用了改进的JADE[16]。变异运算符修改为

其中，Ar，G是的共享存档中随机选择的非支配解决方案。不同的个体受存档中不同的非主导方案的指导，这在一定程度上促进了子群体沿PF搜索。
如果存档为空，则可以从其他子种群中的最佳个体中随机选择Ar，G。
附加差值项用于共享来自存档的信息，因此，单个不仅可以使用来自其自己的子种群的搜索信息，还可以使用来自其他种群的信息。
个体被期望通过使用所有种群的信息沿着整个PF搜索，而不是仅仅被自己的子种群的搜索信息吸引到边缘或极点。因此，CMODE可以在存档信息的帮助下快速近似整个PF。
然后分别使用原始DE中由（5）和（6）定义的交叉和选择运算符。请注意，在JADE中，每个个体i与其自身的突变因子Fi和CRi相关。如果试验向量Ui，G优于父Xi，G，即适应度改进为正值，则（6）中的选择算子称为成功更新。因此，用于生成Ui、G的控制参数Fi和CRi分别称为成功变异因子和成功交叉概率。
单个Xm i的自适应参数Fm i和CRmi设置如下[16]。在每一代G中，Fm i根据位置参数μmF和比例参数0.1的柯西分布独立生成，如下所示：

如果Fm i≥1，则截断为1，如果Fm i≤ 0则再生.
将表示为G代所有成功突变因子的集合。
Cauchy分布的位置参数μmF初始化为0.5，然后在每代结束时更新如下：


同样，在每一代G中，CRmi根据平均μm CR和标准偏差0.1的正态分布独立生成，如下所示：

然后，它被截断为[0，1]。将Sm CR表示为G代所有成功交叉概率的集合。平均μm CR初始化为0.5，然后在每代结束时更新，如下所示：

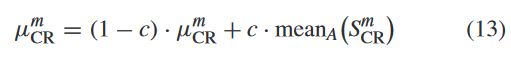
其中c是介于0和1之间的正常数（c=0.1 in JADE），meanA（·）是算术平均值。
备注1：正如[15]所指出的，F和CR的不同值可能必须用于不同的目标。在本文中，Fmi和CRmi可以适应多个目标。
备注2：根据帕累托优势的概念，单目标子种群的每次成功更新都会产生一个新的后代解决方案，该方案要么主导其父母，要么不主导其父母。因为后代至少有一个目标优于其父母。这两种情况分别在一定程度上促进了子种群实现趋同和多样性目标。

DE用于归档填充
归档填充用于维护到目前为止找到的所有非支配解决方案，并指导整个PF的搜索。因此，DE还应进一步改进它，为子种群提供良好的指导信息。归档搜索允许归档成员之间交换信息，这可以加快更好的解决方案的传播，并增强归档的多样性。
对于存档种群，采用jDE[17]中的变异算子

然后使用（5）所述的交叉。在每一代，每个个体的G、Fi和CRi设置为[17]

使用jDE，当前存档种群A生成其后代种群A′。为什么使用jDE而不是JADE进行归档搜索？
原因描述如下。单目标优化中的学分分配很简单，因此通常根据适应度改进的质量来定义。
因此，在单目标子种群中，使用一对一贪婪选择方案，成功的交叉概率SCR、成功的变异因子SF和最佳个体Xbest可以在成功更新后轻松计算或决定。
但是，应重新定义归档中的成功更新和Xbest，因为由于目标冲突，非支配解决方案的适用性改进更为复杂。因此，不能直接采用JADE的参数自适应方案和变异算子。相比之下，jDE中的参数自适应不需要任何信用分配，只需使用一个随机性可控的简单方案。此外，jDE中的变异运算符不使用Xbest。因此，为了简单起见，归档搜索采用了jDE。

存档更新方案
首先，收集M个子种群、当前存档种群A及其后代种群A′生成的所有解，并将其组合在一起。
然后从组合解中提取所有非支配解。获得的所有非支配解决方案都被设置为新的归档成员。
在这一步之后，我们需要检查归档的大小是否超过了预定义的大小限制，因为非支配解决方案的数量可能很大，而且维护它们的计算复杂性很高。
存档截断过程是选择不太拥挤的解决方案，并根据多样性估计丢弃密集分布的存档成员。
在NSGA-II的拥挤距离估计器中，当目标数量大于两个时，可能会得到个人密度的错误估计[36]。
采用并修改了强度帕累托进化算法II（SPEA-II）[37]中引入的第k个最近邻密度估计量，以截断存档。
在第k个最近邻密度估计器中，任何点的密度都是到第k个最接近数据点的距离的（递减）函数。
因此，到第k个最近邻居的距离的倒数只是密度估计值。
更具体地说，对于每个个体Xi，计算目标空间中到档案中所有个体Yj的距离，并将其存储在列表中。
在按递增顺序对列表排序后，第k个元素给出了所需的距离，表示为σk i。k通常设置为等于存档大小的平方根，即k=√|A|。
然后，对应于Xi的密度D（Xi）定义如下：

其中，在分母中添加2，以确保0

本文使用归一化最近邻距离，可以更准确地评估非支配解的拥挤程度。

完整的CMODE在算法1中描述。在初始化过程中，存档A被设置为空。然后随机初始化每个子群中包含NP个体的M个子群。最后，通过从所有子总体中提取非支配解决方案来更新归档总体A。
在每一代中，每个个体都根据第III-B节中描述的程序进行更新。在更新所有子种群后，首先根据第III-C节中描述的程序对存档种群A进行进化，然后在生成结束时根据第III-D节中所描述的存档更新方案进行更新。重复此过程，直到满足终止标准。最后，输出档案A中的解决方案。

CMODE的运行时间主要取决于SPEA-II第k个最近邻密度估计值截断算子的复杂度，因此CMODE复杂度为类似于SPEA-II[37]，即O（L3），其中L=2·|A|+M·NP。然而，如[37]所述，平均而言，复杂性将更低（O（L2 log L））。

扩展到多目标优化
大多数现有的MOEA是针对具有两个或三个目标的问题而设计和测试的[1]。
随着目标数量的增加，他们的表现往往会恶化。大多数经典的基于帕累托的算法，如NSGA-II和SPEA-II，不能为大多数目标问题的PF提供足够的选择压力。
一个主要原因是，随着目标数量的增加，非支配解决方案在种群中的比例往往会变得很大。
这使得基于帕累托优势关系的初选准则无法区分解，而基于密度的二次选择准则在算法的匹配和环境选择中都起着主导作用[38]。虽然本文的主要目的不是解决许多客观问题，但我们仍然尝试扩展CMODE来处理这些问题。
为此，CMODE中引入了基于移位的密度估计（SDE）策略[36]，用于归档截断。许多客观问题的扩展CMODE表示为CMODE+SDE。
通常，密度估计技术通过考虑个体与种群中其他个体之间的相互位置关系来估计个体的密度。群体P中个体X的密度可表示如下：

其中Yi∈ P和Yi !=X；N是P的大小，dist（X，Y）是个体X和Y之间的相似度，通常用它们的欧几里得距离来衡量。D（）是感兴趣个体与群体中其他个体之间相似程度的函数。D（）的实现取决于MOEA中使用的密度估计器。

当估计个体X的密度时，SDE根据这些个体与X在每个目标上的收敛性比较，移动群体中其他个体的位置。具体地说，如果一个人在某个目标上表现得比X好，那么他将被转移到X在这个目标上的相同位置；则他保持不变。

考虑到最小MOP，群体P中个体X的偏移密度SD（X，P）可以描述如下：
其中Y′i是单个Yi的移位版本。Y′i定义如下：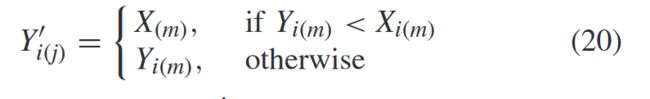

其中X（m）、Yi（m）和Y′i（m∈ （1，2，…，M））个体X，Yi和Y′i的目标值。
SDE的主要思想是通过将高密度值放入拥挤区域，将其分配给收敛较差的解。
然后，可以通过基于密度的第二选择准则来过滤那些收敛较差的解。
SDE可以应用于CMODE的密度估计器，只需使用个体的移位版本来计算距离。SDE的实现很简单，计算成本可以忽略不计，并且不需要额外的参数。

CMODE的特点
CMODE具有以下特点。
1） 它非常简单，并且使用了具有MOP自适应参数的先进单目标DE。
2） DE在两个层次上进行合作：a）一个在单目标亚群之间，b）另一个在亚群和档案群之间。
CMODE也可以被认为是使用主从模型的并行MOEA，其中单目标子群体是从处理器（工人），而归档群体是中央处理器。这将为开发高效的并行MOEA提供一些启示[24]。3） CMODE不仅可以解决两个和三个目标问题，而且可以解决许多目标问题。
CMODE使用多个群体来处理多个目标，而不是传统的基于帕累托的方法中由同一群体作为一个整体来处理所有目标。每个群体只处理一个目标，所有群体合作来近似整个PF。乍一看，CMODE似乎比一般的基于帕累托的方法更复杂，因为它管理多个种群。事实上，CMODE非常简单。与传统方法相比，CMODE的优点如下。
1） 在归档总体中，搜索直接在找到的所有非主导解决方案上执行。然后，只使用一个基本的帕累托优势比较算子来收集非优势解。不需要采用任何复杂的适应度分配方案，如NSGA-II中采用的非支配排序程序，来对优秀的个体进行排序和选择，因为存档群体中的所有非支配解决方案基本上都属于同一个排序。

In each subpopulation, the single-objective optimization process is followed and directly implemented on each objective, thus the individuals are not confused by different conflicting objectives anymore. It is also not necessary to adopt a complicated fitness assignment scheme to rank and select good individuals.
2）在每个子种群中，遵循单目标优化过程并直接执行到每个目标上，个体不再被不同的冲突目标所迷惑。也不需要采用复杂的适应度分配方案来对优秀个体进行排序和选择。
3） 用于聚焦搜索的每个子群体和用于全局搜索的存档群体协作以近似整个PF。实验结果讨论了合作行为

CMODE和CMPSO都是基于多种群的算法，因此具有相似的种群结构。但是CMODE在算法设计和实验研究方面是独特的。与CMPSO相比，CMODE在算法设计方面具有几个特点。
1） 自适应DE用于每个单目标亚群。
2） 自适应DE也用于归档演变。
3） 引入了一种先进的归档更新策略来解决许多客观问题。也就是说，CMODE中的三个主要组件与CMPSO中的不同。在实验研究方面，本文具有以下两个特点。
1） CMODE已经在两个、三个和多个目标优化问题上进行了测试，而CMPSO主要在两个目标问题上进行测试。
2） 通过研究算法的在线搜索行为，深入讨论了子种群和存档种群如何合作生成非支配解以近似整个PF。