【Python数据科学手册】Numpy(全章节)
文章目录
-
- 一、理解Python中的数据类型
-
- 1.Python整型
- 2.Python列表
- 3.Python中的固定类型数组
- 4.从Python列表创建数组--np.array(list)
-
- 1).从列表创建数组
- 2).数组必须包含同一类型的数据,否则类型向上转换
- 3).用dtype关键字明确设置数据类型
- 4).多维数组
- 5.内置方法创建数组
-
- 1).0值数组np.zeros
- 2).1值数组--np.ones
- 3).同值填充数组--np.full
- 4).均匀分布数组--np.linspace
- 5).序列数组--np.arange
- 6).0-1均匀分布随机数数组--np.random.random(size)
- 7).常量分布随机数数组--np.random.normal
- 8).指定区间内的整型随机数数组(左包含)--np.random.randint
- 9).单位矩阵--np.eye
- 10).未初始化数组--np.empty
- 6.Numpy标准数组类型
- 二、Numpy数组基础
-
- 1.Numpy数组的属性
-
- 1).数组的维度 ndim、每个维度的大小 shape、数组的总大小 size=每个维度的乘积
- 2).数组的数据属性 dtype
- 3).每个数组字节大小itemsize(单位bytes)
- 4).数组总字节大小 nbytes=itemsize*size
- 2.数组索引:获取单个元素 x[i,j,k...]
-
- 1).获取数据
- 2).索引赋值
- 3.数组切片:获取子数组 x[start:stop:step,start:stop:step...]
-
- 1).一维子数组
- 2).多维子数组
- 3).获取数组的行和列
- 4).非副本视图的子数组
- 5).创建数组的副本 copy()
- 4.数组的变形 reshape()\newaxis
- 5.数组拼接和分裂
-
- 1).数组的拼接 np.concatenate、 np.vstack 、np.hstack
- 2).数组的分裂 np.split、 np.hsplit 和 np.vsplit
- 三、Numpy数组的计算:通用函数
-
- 1.缓慢的循环
- 2.通用函数介绍
- 3.探索Numpy的通用函数
-
- 1).数组的运算
- 2).绝对值np.absolute
- 3).三角函数
- 4).指数和对数np.exp|np.power、np.log
- 5).点积 np.dot
- 6).专用的通用函数
- 4.高级的通用函数特征
-
- 1).指定输出
- 2).聚合
- 3).外积
- 5.通用函数:更多的信息
- 四、聚合:最小值、最大值和其他值
-
- 1.数组值求和np.sum
- 2.最小值和最大值np.min()\np.max()
-
- 1).多维度聚合
- 2).其它聚合函数
- 3.示例:美国总统的身高是多少
- 五、数组的计算:广播
-
- 1.广播的介绍
- 2.广播的规则
- 3.广播的实际应用
-
- 1).数组的归一化
- 2).二维数组
- 六、比较、掩码和布尔逻辑
-
- 1.示例:统计下雨天数
- 2.和通用函数类似的比较操作
- 3.操作布尔数组
-
- 1).统计记录的个数np.count_nonzero(条件)、np.sum(条件)
- 2).布尔运算符
- 4.将布尔数组作为掩码
- 七、花哨的索引
-
- 1.探索花哨的索引
- 2.组合索引
- 3.示例:选择随机点
- 4.用花哨的索引修改值
- 5.实例:数据区间划分
- 八、数组的排序
-
- 1.Numpy中的快速排序:np.sort和np.argsort
- 2.部分排序:分割np.partition
- 3.示例:K个最近值
- 九、结构化数据:Numpy的结构化数组
-
- 1.生成结构化数组
- 2.更高级的符合类型
- 3.记录数组:结构化数组的扭转
- 4.关于Pandas
- 十、积累补充
一、理解Python中的数据类型
- Python是动态语言,相对于静态语言(如C或Java)往往需要每一个变量都明确地声明,动态语言可以跳过该过程,因此更具有易用性。
- 这种灵活性也指出一个事实:Python变量不仅是他们的值,还包括了有关值得类型的一些额外信息。
1.Python整型
- 当一个整形赋值给一个变量时,这里的Pyhton整形并不是一个“原生”的整形,而是一个指针,指向一个C语言的复合结构体,结构体里面包含一些值。
- Pyhton整形本质上是一个指向包含这个 Python 对象所有信息的某个内存位置的指针,其中包括可以转换成整型的字节。
2.Python列表
- Python 中的标准可变多元素容器是列表,为了获得这些灵活的类型,列表中的每一项必须包含各自的类型信息、引用计数和其他信息;也就是说,每一项都是一个完整的Python 对象。
- 如果列表中的所有变量都是同一类型的,那么很多信息都会显得多余——将数据存储在固定类型的数组中应该会更高效。
3.Python中的固定类型数组
- Python 提供了几种将数据存储在有效的、固定类型的数据缓存中的选项。
- 如内置的数组(array)模块,以及更实用的 NumPy 包中的 ndarray 对象等。
#导包并查看文档
import numpy as np
np?
4.从Python列表创建数组–np.array(list)
1).从列表创建数组
li=[1,2,3,4,5]
np.array(li)
array([1, 2, 3, 4, 5])
备注:array转listtolist
ar=np.array([1,2,3,4,5])
ar.tolist()
>>>[1,2,3,4,5]
2).数组必须包含同一类型的数据,否则类型向上转换
li=[1,2,3.14,0.44,5]#整型->浮点型
np.array(li)
array([1. , 2. , 3.14, 0.44, 5. ])
3).用dtype关键字明确设置数据类型
np.array(li,dtype='int')
array([1, 2, 3, 0, 5])
4).多维数组
mul=[(range(i,i+2)) for i in [1,2,5]]#
np.array(mul)
array([[1, 2],
[2, 3],
[5, 6]])
#mul本身是一个嵌套列表
mul=[list(range(i,i+2)) for i in [1,2,5]]
mul
[[1, 2], [2, 3], [5, 6]]
5.内置方法创建数组
1).0值数组np.zeros
np.zeros(10,int)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
np.zeros((3,5),int)
array([[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]])
2).1值数组–np.ones
np.ones((3,5),int)
array([[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1]])
3).同值填充数组–np.full
np.full((3,5),3.14)
array([[3.14, 3.14, 3.14, 3.14, 3.14],
[3.14, 3.14, 3.14, 3.14, 3.14],
[3.14, 3.14, 3.14, 3.14, 3.14]])
4).均匀分布数组–np.linspace
np.linspace(0,1,5)
array([0. , 0.25, 0.5 , 0.75, 1. ])
5).序列数组–np.arange
np.arange(0,20,2)
array([ 0, 2, 4, 6, 8, 10, 12, 14, 16, 18])
6).0-1均匀分布随机数数组–np.random.random(size)
np.random.random((3,5))
array([[0.36715504, 0.23122403, 0.99571161, 0.79111335, 0.87343738],
[0.69179874, 0.92618523, 0.80521124, 0.53529764, 0.64511412],
[0.68183361, 0.50713411, 0.03999843, 0.33536741, 0.28917038]])
7).常量分布随机数数组–np.random.normal
#高斯分布数组(正太分布,均值是0,方差是1)np.random.normal
np.random.normal(0,1,(3,5))
array([[ 1.34136841, 0.90028157, -1.3556751 , 1.88559225, 0.70577796],
[-1.24864843, -0.5293271 , -0.8958787 , 0.93267372, -0.27102509],
[ 0.28722214, 1.30020621, -0.6223312 , -0.07400186, -0.9309963 ]])
8).指定区间内的整型随机数数组(左包含)–np.random.randint
np.random.randint(0,10,(3,5))
array([[6, 0, 1, 8, 0],
[9, 6, 3, 9, 9],
[3, 6, 1, 9, 2]])
注意:其它np.random方法参考 https://blog.csdn.net/u012149181/article/details/78913167
9).单位矩阵–np.eye
np.eye(3)
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
10).未初始化数组–np.empty
np.empty(3)
array([1., 1., 1.])
6.Numpy标准数组类型
- NumPy 数组包含同一类型的值,因此详细了解这些数据类型及其限制是非常重要的
- 构建数组时,可以使用字符串参数来制定数据类型
np.zeros(10,dtype='int')
np.zeros(10,dtype=int)
np.zeros(10,int)
np.zeros(10,'int')
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
- Numpy标准数组类型
| 数据类型 | 描述 |
|---|---|
| bool_ | 布尔值(真、 True 或假、 False),用一个字节存储 |
| int_ | 默认整型(类似于 C 语言中的 long,通常情况下是 int64 或 int32) |
| intc | 同 C 语言的 int 相同(通常是 int32 或 int64) |
| intp | 用作索引的整型(和 C 语言的 ssize_t 相同,通常情况下是 int32 或 int64) |
| int8 | 字节(byte,范围从 –128 到 127) |
| int16 | 整型(范围从 –32768 到 32767) |
| int32 | 整型(范围从 –2147483648 到 2147483647) |
| int64 | 整型(范围从 –9223372036854775808 到 9223372036854775807) |
| uint8 | 无符号整型(范围从 0 到 255) |
| uint16 | 无符号整型(范围从 0 到 65535) |
| uint32 | 无符号整型(范围从 0 到 4294967295) |
| uint64 | 无符号整型(范围从 0 到 18446744073709551615) |
| float_ | float64 的简化形式 |
| float16 | 半精度浮点型:符号比特位, 5 比特位指数(exponent), 10 比特位尾数(mantissa) |
| float32 | 单精度浮点型:符号比特位, 8 比特位指数, 23 比特位尾数 |
| float64 | 双精度浮点型:符号比特位, 11 比特位指数, 52 比特位尾数 |
| complex_ | complex128 的简化形式 |
| complex64 | 复数,由两个 32 位浮点数表示 |
| complex128 | 复数,由两个 64 位浮点数表示 |
二、Numpy数组基础
1.Numpy数组的属性
np.random.seed(0)#设置随机种子,每次线执行一下,生成的随机数才会次次相同
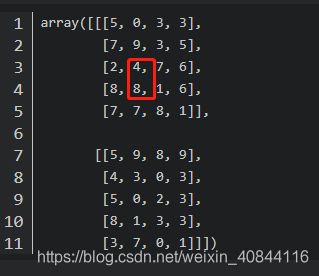
x=np.random.randint(10,size=(2,5,4))
x
array([[[5, 0, 3, 3],
[7, 9, 3, 5],
[2, 4, 7, 6],
[8, 8, 1, 6],
[7, 7, 8, 1]],
[[5, 9, 8, 9],
[4, 3, 0, 3],
[5, 0, 2, 3],
[8, 1, 3, 3],
[3, 7, 0, 1]]])
1).数组的维度 ndim、每个维度的大小 shape、数组的总大小 size=每个维度的乘积
#数组的维度ndim、每个维度的大小shpape、数组的总大小size=每个维度的乘积
print(x.ndim,x.shape,x.size)
3 (2, 5, 4) 40
2).数组的数据属性 dtype
#数组的数据属性dtype
print(x.dtype)
int32
3).每个数组字节大小itemsize(单位bytes)
#每个数组字节大小itemsize(单位bytes)
print(x.itemsize)
4
4).数组总字节大小 nbytes=itemsize*size
#数组总字节大小nbytes=itemsize*size
print(x.nbytes)
160
2.数组索引:获取单个元素 x[i,j,k…]
1).获取数据
x[0]
array([[5, 0, 3, 3],
[7, 9, 3, 5],
[2, 4, 7, 6],
[8, 8, 1, 6],
[7, 7, 8, 1]])
#x[0][0]
x[0,0]
array([5, 0, 3, 3])
#x[0][0][0]
x[0,0,0]
5
2).索引赋值
#赋值修改
x[0,0,0]=3.1415927#numpy数组类型固定,福德值将会被截断或向上转换
x
array([[[3, 0, 3, 3],
[7, 9, 3, 5],
[2, 4, 7, 6],
[8, 8, 1, 6],
[7, 7, 8, 1]],
[[5, 9, 8, 9],
[4, 3, 0, 3],
[5, 0, 2, 3],
[8, 1, 3, 3],
[3, 7, 0, 1]]])
3.数组切片:获取子数组 x[start:stop:step,start:stop:step…]
1).一维子数组
x1=np.arange(10)
x1
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
x1[::]#默认值 start=0、 stop= 维度的大小(size of dimension) 和 step=1
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
x1[:5]#前5个元素
array([0, 1, 2, 3, 4])
x1[5:]#之后的元素
array([5, 6, 7, 8, 9])
x1[4:7]#中间的子数组
array([4, 5, 6])
x1[::2]#隔一个元素
array([0, 2, 4, 6, 8])
x1[2::2]#先定位起始位置再计算步长
array([2, 4, 6, 8])
x1[::-1]#步长是负数,代表逆序
array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
x1[4::-2]#先逆序,再对逆序的结果取步长
array([4, 2, 0])
2).多维子数组
np.random.seed(0)#设置随机种子,每次线执行一下,生成的随机数才会次次相同
x3=np.random.randint(10,size=(2,5,4))
x3
array([[[5, 0, 3, 3],
[7, 9, 3, 5],
[2, 4, 7, 6],
[8, 8, 1, 6],
[7, 7, 8, 1]],
[[5, 9, 8, 9],
[4, 3, 0, 3],
[5, 0, 2, 3],
[8, 1, 3, 3],
[3, 7, 0, 1]]])
x3[:1,2:4,1:2]#依次从各个维度切片
array([[[4],
[8]]])
x3[::-1]#对第一个维度逆序
array([[[5, 9, 8, 9],
[4, 3, 0, 3],
[5, 0, 2, 3],
[8, 1, 3, 3],
[3, 7, 0, 1]],
[[5, 0, 3, 3],
[7, 9, 3, 5],
[2, 4, 7, 6],
[8, 8, 1, 6],
[7, 7, 8, 1]]])
x3[::-1,::-1]#对第一个维度逆序后,对第二个维度逆序
array([[[3, 7, 0, 1],
[8, 1, 3, 3],
[5, 0, 2, 3],
[4, 3, 0, 3],
[5, 9, 8, 9]],
[[7, 7, 8, 1],
[8, 8, 1, 6],
[2, 4, 7, 6],
[7, 9, 3, 5],
[5, 0, 3, 3]]])
x3[::-1,::-1,::-1]#依次对各个维度逆序
array([[[1, 0, 7, 3],
[3, 3, 1, 8],
[3, 2, 0, 5],
[3, 0, 3, 4],
[9, 8, 9, 5]],
[[1, 8, 7, 7],
[6, 1, 8, 8],
[6, 7, 4, 2],
[5, 3, 9, 7],
[3, 3, 0, 5]]])
3).获取数组的行和列
- 切片可以取到子数组,维度不变,索引可以取到低维度的数组或元素。结合切片和数组,可以灵活区数,例如单列或单行。
x3[0,0]#取行,方法同索引
array([5, 0, 3, 3])
x3[0,:,0]#取列,结合索引和切片
array([5, 7, 2, 8, 7])
4).非副本视图的子数组
- 数组的切片结果不是一个与原数组无关的副本,而是原数组数据的视图,改变这个视图,会对原数组产生影响。
x1_slice=x1[2:5]
x1_slice
array([2, 3, 4])
x1_slice[0]=22
x1
array([ 0, 1, 22, 3, 4, 5, 6, 7, 8, 9])
- 这个特点与python列表不同,列表的切片发生改变不会影响原列表
list1=list(range(10))
list1_slice=list1[2:5]
list1_slice[0]=22
list1
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
5).创建数组的副本 copy()
- 如果元创建数组的副本,需要使用copy()方法
x1=np.arange(10)
x1_slice_copy=x1[2:5].copy()
x1_slice_copy
array([2, 3, 4])
x1_slice_copy[0]=22
x1
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
4.数组的变形 reshape()\newaxis
- 使用reshape()函数,可以改变数组的形状,但是需要保证数组大小不变
x1=np.arange(24)
x_rsh=x1.reshape(2,3,4)#保证数组大小一致
x_rsh
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
- 使用reshape方法或者newaxis关键字可以将一维数组转变为二维行或列矩阵
xli=np.array([1,2,3])#一维数组
xli
array([1, 2, 3])
xli.reshape(1,3)#矩阵:单行向量
array([[1, 2, 3]])
xli[np.newaxis,:]
array([[1, 2, 3]])
xli.reshape(3,1)#矩阵:单列向量
array([[1],
[2],
[3]])
xli[:,np.newaxis]
array([[1],
[2],
[3]])
EXTEND:行列转置
i=np.transpose(b)
i.T
5.数组拼接和分裂
1).数组的拼接 np.concatenate、 np.vstack 、np.hstack
- 注意:np.concatenate拼接的数组需要相同的维数,除了合并方向,其他维度结构要一致
#np.concatenate
x=np.array([1,2,3])
y=np.array([11,22,33])
z=np.array([111,222,332])
ct=np.concatenate([x,y,z])
ct#多个一维数组拼接成一个长的一维数组
array([ 1, 2, 3, 11, 22, 33, 111, 222, 332])
x2=np.array([[4,5,6],[7,8,9]])
y2=np.array([[44,55,66],[77,88,99]])
z2=np.array([[444,555,666],[777,888,999]])
#np.concatenate([x2,y2])
np.concatenate((x2,y2))#两个二位数组拼成一个多行的二位数组
array([[ 4, 5, 6],
[ 7, 8, 9],
[44, 55, 66],
[77, 88, 99]])
- np.vstack垂直方向上拼接(行拼接)
#np.vstack((x,x2))
vt=np.vstack([x,x2])
vt
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
- np.hstack水平方向上拼接(列拼接)
h=np.array([99,99]).reshape(2,1)#单列
ht=np.hstack((x2,h))
ht
array([[ 4, 5, 6, 99],
[ 7, 8, 9, 99]])
- np.dstac按顺序深入(第三维)
dt=np.dstack((x2,y2,z2))
dt
array([[[ 4, 44, 444],
[ 5, 55, 555],
[ 6, 66, 666]],
[[ 7, 77, 777],
[ 8, 88, 888],
[ 9, 99, 999]]])
2).数组的分裂 np.split、 np.hsplit 和 np.vsplit
- np.split 分裂点的索引位置,N个分裂点产生N+1个子数组
np.split(ct,[2,5]))#有两个分裂点,分别在位置2和位置5
[array([1, 2]), array([ 3, 11, 22]), array([ 33, 111, 222, 332])]
- np.vsplit 水平分裂
x,y=np.vsplit(vt,[1])
x
array([[1, 2, 3]])
y
array([[4, 5, 6],
[7, 8, 9]])
- np.hsplit垂直分裂
x,y=np.hsplit(ht,[3])
x
array([[4, 5, 6],
[7, 8, 9]])
y
array([[99],
[99]])
- np.dsplit第三维分裂
x,y=np.dsplit(dt,[2])
x
array([[[ 4, 44],
[ 5, 55],
[ 6, 66]],
[[ 7, 77],
[ 8, 88],
[ 9, 99]]])
y
array([[[444],
[555],
[666]],
[[777],
[888],
[999]]])
三、Numpy数组的计算:通用函数
1.缓慢的循环
Python 的默认实现(被称作 CPython)处理起某些操作时非常慢,一部分原因是该语言的动态性和解释性——数据类型灵活的特性决定了序列操作不能像 C 语言和 Fortran 语言一样被编译成有效的机器码。
NumPy 的通用函数可以用来替代循环,以快速实现数组的逐元(elementwise)运算。
2.通用函数介绍
NumPy 为很多类型的操作提供了非常方便的、静态类型的、可编译程序的接口,也被称作向量操作。
NumPy 中的向量操作是通过通用函数实现的。
标量和数组,数组和数组,一维及多维。
1/ np.arange(1, 6)
np.arange(5) / np.arange(1, 6)
2**np.arange(5)
3.探索Numpy的通用函数
通用函数有两种存在形式: 一元通用函数(unary ufunc)对单个输入操作, 二元通用函数(binary ufunc)对两个输入操作。
1).数组的运算
x = np.arange(4)
print("x =", x)
print("x + 5 =", x + 5)
print("x - 5 =", x - 5)
print("x * 2 =", x * 2)
print("x / 2 =", x / 2)
print("x // 2 =", x // 2)
print("-x = ", -x)
print("x ** 2 = ", x ** 2)
print("x % 2 = ", x % 2)
x = [0 1 2 3]
x + 5 = [5 6 7 8]
x - 5 = [-5 -4 -3 -2]
x * 2 = [0 2 4 6]
x / 2 = [0. 0.5 1. 1.5]
x // 2 = [0 0 1 1]
-x = [ 0 -1 -2 -3]
x ** 2 = [0 1 4 9]
x % 2 = [0 1 0 1]
| 运算符 | 对应的通用函数 | 描述 |
|---|---|---|
| + | np.add | 加法运算(即 1 + 1 = 2) |
| - | np.subtract | 减法运算(即 3 - 2 = 1) |
| - | np.negative | 负数运算(即 -2) |
| * | np.multiply | 乘法运算(即 2 * 3 = 6) |
| / | np.divide | 除法运算(即 3 / 2 = 1.5) |
| // | np.floor_divide | 地板除法运算(floor division,即 3 // 2 = 1) |
| ** | np.power | 指数运算(即 2 ** 3 = 8) |
| % | np.mod | 模 / 余数(即 9 % 4 = 1) |
2).绝对值np.absolute
x = np.array([-2, -1, 0, 1, 2])
abs(x)#1
np.absolute(x)#2
np.abs(x)#3
array([2, 1, 0, 1, 2])
当处理复数时,绝对值返回的是该复数的幅度
3).三角函数
| 正三角函数 | 逆三角函数 |
|---|---|
| np.sin() | np.arcsin() |
| np.cos() | np.arccos() |
| np.tan() | np.arctan() |
print("theta = ", theta)
print("sin(theta) = ", np.sin(theta))
print("cos(theta) = ", np.cos(theta))
print("tan(theta) = ", np.tan(theta))
theta = [0. 1.57079633 3.14159265]
sin(theta) = [0.0000000e+00 1.0000000e+00 1.2246468e-16]
cos(theta) = [ 1.000000e+00 6.123234e-17 -1.000000e+00]
tan(theta) = [ 0.00000000e+00 1.63312394e+16 -1.22464680e-16]
x = [-1, 0, 1]
print("x = ", x)
print("arcsin(x) = ", np.arcsin(x))
print("arccos(x) = ", np.arccos(x))
print("arctan(x) = ", np.arctan(x))
x = [-1, 0, 1]
arcsin(x) = [-1.57079633 0. 1.57079633]
arccos(x) = [3.14159265 1.57079633 0. ]
arctan(x) = [-0.78539816 0. 0.78539816]
4).指数和对数np.exp|np.power、np.log
指数
x = [1, 2, 3]
print("x =", x)
print("e^x =", np.exp(x))
print("2^x =", np.exp2(x))
print("3^x =", np.power(3, x))
x = [1, 2, 3]
e^x = [ 2.71828183 7.3890561 20.08553692]
2^x = [2. 4. 8.]
3^x = [ 3 9 27]
对数
x = [1, 2, 4, 10]
print("x =", x)
print("ln(x) =", np.log(x))
print("log2(x) =", np.log2(x))
print("log10(x) =", np.log10(x))
x 的值很小时,以上函数给出的值比 np.log 和 np.exp 的计算更精确
x = [1, 2, 4, 10]
ln(x) = [0. 0.69314718 1.38629436 2.30258509]
log2(x) = [0. 1. 2. 3.32192809]
log10(x) = [0. 0.30103 0.60205999 1. ]
x = [0, 0.001, 0.01, 0.1]
print("exp(x) - 1 =", np.expm1(x))
print("log(1 + x) =", np.log1p(x))
x = [0, 0.001, 0.01, 0.1]
print("exp(x) - 1 =", np.expm1(x))
print("log(1 + x) =", np.log1p(x))
5).点积 np.dot
np.dot([1,2,3],[4,5,6])
#=1*4 + 2*5 + 3*6=32
>>>32
6).专用的通用函数
更加专用,也更加晦涩的通用函数优异来源是子模块 scipy.special
Scipy是基于Numpy创建的Python 科学计算核心库,提供了众多数学算法与函数。
4.高级的通用函数特征
1).指定输出
所有的通用函数都可以通过 out 参数来指定计算结果的存放位置.
x = np.arange(5)
y = np.empty(5)
np.multiply(x, 10, out=y)
print(y)
[ 0. 10. 20. 30. 40.]
这个特性也可以被用作数组视图
y = np.zeros(10)
np.power(2, x, out=y[::2])
print(y)
[ 1. 0. 2. 0. 4. 0. 8. 0. 16. 0.]
创建一个临时数组
np.power(2, x, out=2 ** x)
array([ 1, 2, 4, 8, 16], dtype=int32)
2).聚合
不同通用函数的聚合方法会适应改函数而变化。
reduce 方法:将数组的维度减少一维
accumulate:显示中途计算过程值
x = np.arange(1, 6)
np.add.reduce(x) #加法聚合就是元素累加
15
np.add.accumulate(x)
array([ 1, 3, 6, 10, 15])
np.multiply.reduce(x)#乘法聚合就是元素累积
120
np.multiply.accumulate(x)
array([ 1, 2, 6, 24, 120])
NumPy 提供了专用的函数(np.sum、 np.prod、 np.cumsum、np.cumprod )
3).外积
任何通用函数都可以用 outer 方法获得两个不同输入数组所有元素对的函数运算结果。
x = np.arange(1, 6)
np.multiply.outer(x, x)
array([[ 1, 2, 3, 4, 5],
[ 2, 4, 6, 8, 10],
[ 3, 6, 9, 12, 15],
[ 4, 8, 12, 16, 20],
[ 5, 10, 15, 20, 25]])
通用函数另外一个非常有用的特性是它能操作不同大小和形状的数组,一组这样的操作被称为广播(broadcasting)
5.通用函数:更多的信息
NumPy(http://www.numpy.org)
SciPy(http://www.scipy.org)
四、聚合:最小值、最大值和其他值
1.数组值求和np.sum
L = np.random.random(100)
sum(L)#内置函数
np.sum(L)
55.612091166049424
2.最小值和最大值np.min()\np.max()
min(L), max(L)#内置函数
np.min(L), np.max(L)
L.min(), L.max()#L.sum()更简洁的写法
1).多维度聚合
M = np.random.randint(0,10,(3,4))
M
array([[5, 3, 1, 7],
[3, 8, 5, 5],
[1, 9, 7, 2]])
默认情况下,每一个 NumPy 聚合函数将会返回对整个数组的聚合结果
axis参数用于指定沿着哪个轴的方向进行聚合
M.sum(),M.sum(axis=1),M.sum(axis=0)
(56, array([16, 21, 19]), array([ 9, 20, 13, 14]))
2).其它聚合函数
| 函数名称 | NaN安全版本 | 描述 |
|---|---|---|
| np.sum | np.nansum | 计算元素的和 |
| np.prod | np.nanprod | 计算元素的积 |
| np.mean | np.nanmean | 计算元素的平均值 |
| np.std | np.nanstd | 计算元素的标准差 |
| np.var | np.nanvar | 计算元素的方差 |
| np.min | np.nanmin | 找出最小值 |
| np.max | np.nanmax | 找出最大值 |
| np.argmin | np.nanargmin | 找出最小值的索引 |
| np.argmax | np.nanargmax | 找出最大值的索引 |
| np.median | np.nanmedian | 计算元素的中位数 |
| np.percentile | np.nanpercentile | 计算基于元素排序的统计值 |
| np.any | N/A | 验证任何一个元素是否为真 |
| np.all | N/A | 验证所有元素是否为真 |
3.示例:美国总统的身高是多少
五、数组的计算:广播
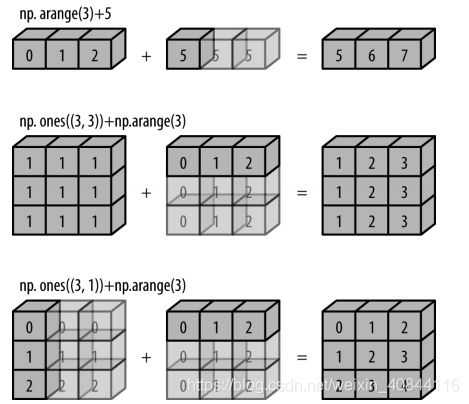
广播可以简单理解为用于不同大小数组的二进制通用函数(加、减、乘等)的一组规则。(数组的自动扩散)
1.广播的介绍
2.广播的规则
• 规则 1:如果两个数组的维度数不相同,那么小维度数组的形状将会在最左边补 1。
两个数组有一个维度相同,且另一维度为1的数组个数至少有1个
np.ones((2, 3))+np.arange(3)
(2, 3)+(1, 3)
==>
(2, 3)+(2, 3)
• 规则 2:如果两个数组的形状在任何一个维度上都不匹配,那么数组的形状会沿着维度为 1 的维度扩展以匹配另外一个数组的形状。
两个数组的两个维度都不相同,但两个数组不同维度互为1
np.ones((2,1))+np.arange(3)
(2, 1)+(1, 3)
==>
(2, 3)+(2, 3)
• 规则 3:如果两个数组的形状在任何一个维度上都不匹配并且没有任何一个维度等于 1,那么会引发异常。
np.ones((3,2))+np.arange(3)
(3, 2)+(1, 3)
不兼容
有一个维度相同X
不同纬度互为1X
3.广播的实际应用
1).数组的归一化
归一化:一组数,每个数减去该组数的平均值,使得元素总和等于0
X-X.mean(axis=0)#多行聚合
X-X.mean(axis=1).reshape((10,1))#多列聚合
2).二维数组
x = np.linspace(0, 5, 50)
y = np.linspace(0, 5, 50)[:, np.newaxis]
z = np.sin(x) ** 10 + np.cos(10 + y * x) * np.cos(x)
六、比较、掩码和布尔逻辑
基于某些准则来抽取、修改、计数或对一个数组中的值进行其他操作时,掩码就可以派上用场了。
1.示例:统计下雨天数
使用通用函数实现数组的逐元素比较
2.和通用函数类似的比较操作
x = np.array([1, 2, 3, 4, 5])
x < 3
array([ True, True, False, False, False])
6种比较操作:
| 运算符 | 对应的通用函数 |
|---|---|
| == | np.equal |
| != | np.not_equal |
| < | np.less |
| <= | np.less_equal |
| > | np.greater |
| >= | np.greater_equal |
3.操作布尔数组
1).统计记录的个数np.count_nonzero(条件)、np.sum(条件)
np.count_nonzero(条件)对True的个数进行计数
np.sum(条件)自动将True计为1
x=np.random.randint(0,10,(5,3))
array([[8, 4, 0],
[5, 3, 9],
[6, 9, 6],
[0, 8, 9],
[6, 8, 5]])
np.count_nonzero(x < 6)
np.sum(x < 6)
>>>6
和其它聚合函数一样,求和也可以沿着行或列进行
np.sum(x < 6, axis=1)
>>>array([2, 2, 0, 1, 1])
判断条件符合存在np.any(),全部np.all()
np.any(x<6)#是否存在满足条件的值
>>>True
np.all(x<6)#所有元素是否都满足条件
False
沿着特定坐标轴判断
np.any(x<6,1)
array([ True, True, False, True, True])
np.all(x<6,0)
array([False, False, False])
2).布尔运算符
多条件:Python 的逐位逻辑运算符(bitwise logic operator) &、 |、 ^ 和 ~ 来实现
np.sum((x>3)&(x<6))
>>>3
| 运算符 | 对应通用函数 |
|---|---|
| & | np.bitwise_and |
| | | np.bitwise_or |
| ^ | np.bitwise_xor |
| ~ | np.bitwise_not |
4.将布尔数组作为掩码
利用比较运算符可以得到一个布尔数组,为了将这些值从数组中选出,可以进行简单的索引,即掩码操作
x<6
array([[False, True, True],
[ True, True, False],
[False, False, False],
[ True, False, False],
[False, False, True]])
x[x<6]
>>>array([4, 0, 5, 3, 0, 5])
import numpy as np
a= np.array([0,1,0,1,0])
b=np.array([11,22,33,44,55])
b[a==0]
>>>array([11, 33, 55])
现在返回的是一个一维数组,它包含了所有满足条件的值
ATTENTION:
and 和 or 判断整个对象是真或假,而 & 和 | 是指每个对象中的比特位。
NumPy 中有一个布尔数组时,该数组可以被当作是由比特字符组成的,其中
1 = True、 0 = False。
记住: and 和 or 对整个对象执行单个布尔运算,而 & 和 | 对一个对象的内
容(单个比特或字节)执行多个布尔运算。对于 NumPy 布尔数组,后者是常用的操作。
七、花哨的索引
花哨的索引和前面那些简单的索引(索引值(如 arr[0])、切片(如 arr[:5])和
布尔掩码(如 arr[arr > 0])获得并修改部分数组)非常类似,但是传递的是索引数组,而不是单个标量。花哨的索引让我们能够快速获得并修改复杂的数组值的子数据集.
1.探索花哨的索引
- 对一维数组
rand = np.random.RandomState(42)#设置随机状态
x = rand.randint(100, size=10)
x
>>>array([51, 92, 14, 71, 60, 20, 82, 86, 74, 74])
#方式1:简单切片
[x[3],x[7],x[4],x[5]]
>>>[71, 86, 60, 20]
#方式二:传递索引列表
ind=[3,7,4,5]
x[ind]
>>>array([71, 86, 60, 20])
#方式三:传递索引数据
ind=np.array([[3,7],
[4,5]])
x[ind]
array([[71, 86],
[60, 20]])
结果的形状与索引数组ind的形状一致.
- 对多维度的应用:
X = np.arange(12).reshape((3, 4))
X
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
row = np.array([0, 1, 2])
col = np.array([2, 1, 3])
X[row, col]
>>>array([ 2, 5, 11])
取值相当于:[X[0, 2],X[1, 1],X[2, 3]]
花哨的索引中,索引值的配对遵循广播的规则。
2.组合索引
1.花哨的索引+简单索引
X[2,[2,1,3]]
>>>array([10, 9, 11])
2.花哨的索引+切片
X[:2,[2,1,3]]
array([[2, 1, 3],
[6, 5, 7]])
3.花哨的索引+掩码
mask = np.array([1, 0, 1, 0], dtype=bool)
X[row[:, np.newaxis], mask]
array([[ 0, 2],
[ 4, 6],
[ 8, 10]])
3.示例:选择随机点
花哨的索引的一个常见用途是从一个矩阵中选择行的子集。
4.用花哨的索引修改值
- 简单赋值修改
x = rand.randint(100, size=10)
ind=[3,7,4,5]
x[ind]=99
x
>>>array([51, 92, 14, 99, 99, 99, 82, 99, 74, 74])`
x[ind] -= 10#自减
x
>>>array([51, 92, 14, 89, 89, 89, 82, 89, 74, 74])`
- 累计赋值
x = np.zeros(10)
x[[0, 0]] = [4, 6]
print(x)
>>>[ 6. 0. 0. 0. 0. 0. 0. 0. 0. 0.]#首先赋值 x[0] = 4,然后赋值 x[0] = 6
i = [2, 3, 3, 4, 4, 4]
x[i] += 1
x
>>>array([ 6., 0., 1., 1., 1., 0., 0., 0., 0., 0.])
这里虽然是自增,但只自增一次,如果累加,可以借助通用函数中的 at() 方法
x = np.zeros(10)
np.add.at(x, i, 1)
print(x)
>>>[ 0. 0. 1. 2. 3. 0. 0. 0. 0. 0.]
5.实例:数据区间划分
八、数组的排序
选择排序
x = np.array([5,2, 1, 4, 3])
for i in range(len(x)):
swap = i + np.argmin(x[i:])#np.argmin最小值所在位置,+i才是在x数组的位置
(x[i], x[swap]) = (x[swap], x[i])#调换位置
BOGO排序
x = np.array([5,2, 1, 4, 3])
while np.any(x[:-1] > x[1:]):#只要存在前一个数字大于后一个数字
np.random.shuffle(x)#随机排列
效率都很低
1.Numpy中的快速排序:np.sort和np.argsort
np.sort快速排序
x = np.array([5,2, 1, 4, 3])
x=np.sort(x)
#或者
x.sort()
np.argsort()排好序的索引
x = np.array([55, 22, 11, 44, 33])
index=np.argsort(x)#最小的数索引是2,次小的在1,稍大的在4,再大的在3,最大的最为在0
index
>>>array([2, 1, 4, 3, 0], dtype=int64)
x[index]#花哨索引
>>>array([11, 22, 33, 44, 55])
x[index)[::-1]]#设置步长为-1,则可逆序
>>>array([55, 44, 33, 22, 11])
axis沿着指定轴方向排序
x=np.random.randint(0,10,(5,3))
np.sort(x,axis=0)
np.sort(x,axis=-1)
2.部分排序:分割np.partition
找到数组中第 K 小的值,np.partition(x,K),输出一个新数组,前K个数就是,后面的无关,但都没有排序。
np.partition(x,K)[:K]
x = np.array([7, 2, 3, 1, 6, 5, 4])
np.partition(x, 3)
>>>array([2, 1, 3, 4, 6, 5, 7])
np.partition(x, 3)[:3]
>>>array([2, 1, 3])
3.示例:K个最近值
九、结构化数据:Numpy的结构化数组
1.生成结构化数组
dtp=np.dtype({'names':('name', 'age', 'weight'),
'formats':('U10', 'i4', 'f8')})
dtp=np.dtype({'names':('name', 'age', 'weight'),
'formats':((np.str_, 10), int, np.float32)})
dtp=np.dtype([('name', 'S10'), ('age', 'i4'), ('weight', 'f8')])
dtp=np.dtype('S10,i4,f8')#忽略名称
data = np.zeros(4, dtype=dtp)
print(data.dtype)
| NumPy数据类型符号 | 描述 | 示例 |
|---|---|---|
| ‘b’ | 字节型 | np.dtype(‘b’) |
| ‘i’ | 有符号整型 | np.dtype(‘i4’) == np.int32 |
| ‘u’ | 无符号整型 | np.dtype(‘u1’) == np.uint8 |
| ‘f’ | 浮点型 | np.dtype(‘f8’) == np.int64 |
| ‘c’ | 复数浮点型 | np.dtype(‘c16’) == np.complex128 |
| ‘S’、 ‘a’ | 字符串 | np.dtype(‘S5’) |
| ‘U’ | Unicode 编码字符串 | np.dtype(‘U’) == np.str_ |
| ‘V’ | 原生数据, raw data(空, void) | np.dtype(‘V’) == np.void |
2.更高级的符合类型
创建一个数据类型,该数据类型用 mat 组件包含一个 3× 3的浮点矩阵
tp = np.dtype([('id', 'i8'), ('mat', 'f8', (3, 3))])
X = np.zeros(1, dtype=tp)
print(X[0])
>>>(0, [[0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0]])
print(X['mat'][0])
>>>[[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
3.记录数组:结构化数组的扭转
np.recarray :域可以像属性一样获取
#data['age']
data_rec = data.view(np.recarray)
data_rec.age
4.关于Pandas
十、积累补充
1.np.where
2.np.column_stack
3.np.unique