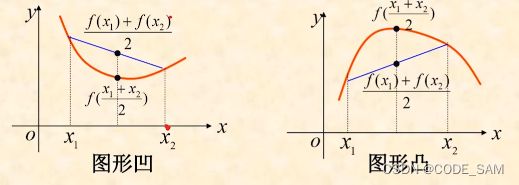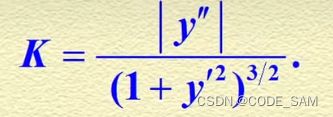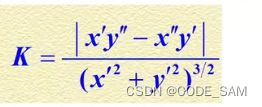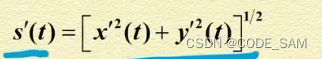高数:微分 函数图像 曲率
目录
微分的定义:
微分几何含义:
微分中值定理:
费马定理
罗尔定理:
拉格朗日中值定理:
柯西中值定理:
洛必达法则:
泰勒公式
小总结:
凹凸性:
极值及其求法:
函数图形的描绘:
曲率:
曲率半径:用圆来模拟的曲率半径
微分的定义:
近似出y的变量,当x变化时
定义:
设y=f(x),x->x+x0
y的增量:y1=f(x+x0)-f(x)
可变成y0=Ax1+o(x0)(y的变化量和x的变化量线性相关,o(x0)称为高阶无穷,A称为线性主部)
变形:dy=Ax0即dy=A*dx (dy是近似值)
可微的充要条件可导:
y0/x0=A+o(x0)/x0
A=f'(x)
理解:Adx即为y近似值的变化,
dy/dx=f‘(x);(此时dy,dx可以分开)
基本微分公式与法则:dy=dx*f’(x)
微分形式不变性:换元求导罢了
d(原函数)=(一阶导)*dt
总结:微分就是求导,为了不定积分打下基础
微分几何含义:
首次y0为变化量,dy为y0的近似值
理解:用切线模拟曲线
当x0趋于0时,y和dy近似相等
微分的近似计算:
y0=f(x)*x0;
f(x0+x)=f‘(x)*x0+f(x0);
注意:x0越大,偏差越大。
微分中值定理:
费马定理
:极大值导数等于0
证明:求出左右极限的范围,因为可导,极限为0
驻点:导数等于0的点,不一定为极值点
罗尔定理:
满足:1.[a,b]连续2.(a,b)可导3.f(a)=f(b)
则存在c属于(a,b),f’(c)为0;
理解,隐含相对于费马定理,存在了最大值或最小值
拉格朗日中值定理:
1.[a,b]连续2.(a,b)可导
存在c属于(a,b),f’(c)=(f(a)-f(b))/(a-b);
理解:任意割线线和某一点的切线斜率相等
罗尔定理相当于把拉格朗日定理的特殊情况
柯西中值定理:
对任意f(x)和F(x)
1.[a,b]连续2.(a,b)可导3.F(x)!=0
(f(b)-f(a))/(F(b)-F(a))=f’(c)/F'(c)
注意右边是一个变量c
三个定理中值:柯西推拉格朗日,令F(x)=x
拉格朗日推罗尔,令f(a)=f(b)
洛必达法则:
前提:0/0 或者无穷/无穷
1.x->a或者无穷时,f(x)->0 F(x)->0(无穷)
2.在a的去心邻域内f‘(x),F’(x)存在且F‘(x)不等于0
3.lim x->0 f'(x)/F'(x)存在极限或者无穷大,还是0/0或者无穷/无穷则继续求导(如果极限不存在,方法无效)
则limx->0f(x)/F(x)=limx->0f'(x)/F'(x)
拓展:0*无穷 无穷-无穷,0^0 1^无穷 无穷^0化成前提条件可以用洛必达
运用:1.检查0/0 或者无穷/无穷
2.求导,再检验0/0 或者无穷/无穷,是,求导,不是,等价无穷小,替换
3.将趋于整数的项项外移,不影响是否极限是否存在的判断
泰勒公式
:用到的少
微分是用一次表达式,泰勒就是用多次表达式1次,2次,3次来模拟函数
P(n)=a0+a1(x-x0)+a2(x-x0)^2……an*(x-x0)*n
此时f(x0)=a0,f’(x0)=a1,f‘’(x0)=2!a2.......
an=f^n(x0)/n!
余项:Rn=o((x-x0)^n)=f(n+1)(A)*(x-x0)^(n+1)/(n+1)!
存在A在x0到x之间使得,多项式完美拟合曲线,当n=0时,就是拉格朗日定理
麦克劳林公式:在0处展开
P(n)=a0+a1/1!+a2/2!......
e^x=1+x+x^2/2!+.......+R(n)
等价无穷小的原理
原理对sinx和cosx进行更高精度的展开
小总结:
1.洛必达法则 2.等价无穷小 3.换元(三角反函数)4.泰勒公式
函数单调性:f'(x)>=0,单调增,<=0,单调减......
讨论单调性:1.驻点=x0,f‘(x0)=0 2.导数不存在的点
凹凸性:
定义:
f(x)是凹的那么-f(x)是凸的
二阶导数正,凹函数,负是凸
理解:切线斜率变化
一可跳二无荡,一阶导数可以跳跃,二阶导数无荡
凸凹性改变的点为拐点,f''(x0)=0,拐点一定符合x0,x0不一定是拐点
x0可以在二阶导无定义
极值及其求法:
极值:邻域内最大小
最值:区域内最大
最值唯一,最值点不唯一
x0为极值点充要条件:f’(x0)=0;f‘’(x0)!=0;
函数图形的描绘:
1.看定义域 奇偶 周期 渐近线(水平,铅锤)
2特殊点x=0;x=1
3.一阶导决定增减性,极值点
4.二阶导决定凹凸性
步骤:1.先求一阶导,再求二阶导
2.求一阶导等于0的解,再求二阶导等于0的根
3.做表
4.一阶导有不被定义的点,原函数有渐进线
二阶导有不被定义的点,一阶导有渐进线
曲率:
简单来说就是:角度变化/弧长
曲率:k=limx->0|a/s|
圆的曲率:1/r
角度变化相同时,弧长越长,曲率越小,所以半径越长,曲率越小
证明y=f(x)设切线与x轴夹角为a,y‘=tana;
y''=seca^2*da/dx
da/dx=y''/seca^2 ds/dx=seca seca^2=1+tanx^2
代入得到结果
对于函数y=f(t)x=g(t)
曲率:
证明tana=f’(t)/g'(t)
a(t)=arctanf'(t)/g'(t)
a't=1/(1+(y'/x')^2)*[(y'/x')^2]'