HLS 3 FPGA并行化 稀疏矩阵向量乘法（计算机视觉）

CRS

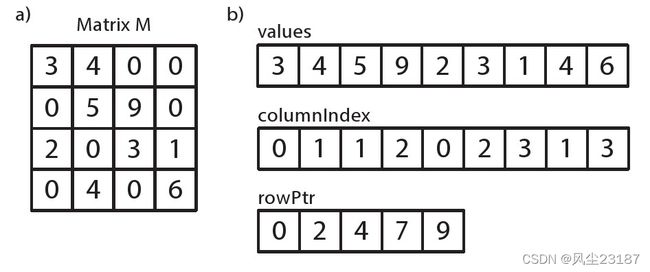
作为一种数据结构，由3个数组组成。值(values)数组保存矩阵中非零元素的值。列索引(columnIndex)数组和行指针（rowPtr）数组对非零元素的位置信息进行编码。列索引存储每个元素的列数，行指针包含每一行第一个元素在values中的索引。CRS 结构避免存储矩阵中的0值，确实在数值数组中确实没有存储0。但是在这个例子中，虽然数值数组不保存0，但是列索引数组和行指针数组作为标记信息，表示了矩阵的形态。CRS 广泛用于大型的矩阵但是仅仅有少量的非零元素（少于10%或者更低），这样可以简化这类矩阵的存储以及相关的运算。

CRS结构也不见得是表示稀疏矩阵最高效的方式，其他稀疏矩阵表示方法也在被使用。
是一种由3个数组组成的数据结构。
但是，CRS对矩阵的稀疏性没有要求，可以适用于任何矩阵。作为一种针对矩阵的通用方法，但不见得是最高效的。CRS结构也不见得是表示稀疏矩阵最高效的方式，其他稀疏矩阵表示方法也在被使用。
更准确的讲，CRS作为一种数据结构由3个数组构成：值(values)、列索引(colIndex)、行索引（rowPtr）。值数组和列索引表示稀疏矩阵M中的每一个非零元素，这些数组表示矩阵M采用行的方式，从左到右，从上到下。矩阵中的数据保存在值数组中，列索引数组保存数据在数组中水平方向的位置，如果 values[k] 表示 M_{ij}M ij 其中collndex[k]= jcollndex[k]=j。数组rowPtr用
n+1n+1的长度来表示n行矩阵。rowPtr[k] 表示在行k之前，矩阵中所有元素的数目，其中rowPtr[0]=0rowPtr[0]=0且最后一个元素rowPtr[k] 总是表示当前矩阵k行之前所有非零元素的个数M_{ij}M ij​ ,其中rowPtr[i] \leq k \leq rowPtr[i+1]rowPtr[i]≤k≤rowPtr[i+1]。如果行k包含任何非0元素，那么owPtr[k] 将包含当前行的第一个元素。注意，如果当前行没有非0元素，那么 rowPtr 数组中的值将会重复出现。从图6.1 a）中，我们可以行优先的方式遍历矩阵，从而确定值（values）数组在CRS中的形式。只要发现一个非0元素，它的值会被保存在下一个索引 ii 中，同时，它的列号columnIndex[i] 会被保存在列数组中。另外，在我们访问一个新行的时候，我们保存下一个值的索引
ii 在rowPtr数组中。所以，rowPtr 数组的第一个元素总是0。从图 6.1 b)中，我们可以把矩阵转换为二位数组表示的方式。第一步是根据rowPtr数组，确定每一行中非0 元素的个数。对行
ii 而言，该行中元素的数目为
rowPtr[i]-rowPtr[i+1]rowPtr[i]−rowPtr[i+1]
的差值。所以当前行的值可以从values数组values[rowPtr[i]] 开始，通过递归得到。在我们的示例矩阵中，因为前 rowPtr 数组前2个元素是0和2，所以我们知道第一行有2个非0元素，即value[0] 和value[1] 。第一个非0元素在values数组中,value[0] 是3。该值所对应的列号为1，因为
columnIndex[0]=0columnIndex[0]=0。以此类推，矩阵中第二行元素的个数为k\in[2,4)k∈[2,4),第三行的元素个数为k \in [4,7)k∈[4,7)。最后，共有9个非0元素在矩阵中，所以rowPtr最后一个值是9

#include "spmv.h"

void spmv(int rowPtr[NUM_ROWS+1], int columnIndex[NNZ],
        DTYPE values[NNZ], DTYPE y[SIZE], DTYPE x[SIZE]){
L1: for (int i = 0; i < NUM_ROWS; i++) {
        DTYPE y0 = 0;
    L2: for (int k = rowPtr[i]; k < rowPtr[i+1]; k++) {
            #pragma HLS unroll factor=8
            #pragma HLS pipeline
            y0 += values[k] * x[columnIndex[k]];
        }
        y[i] = y0;
    }
}

spmv.h：
#ifndef __SPMV_H__
#define __SPMV_H__

const static int SIZE = 4; // SIZE of square matrix
const static int NNZ = 9; //Number of non-zero elements
const static int NUM_ROWS = 4;// SIZE;
typedef float DTYPE;
void spmv(int rowPtr[NUM_ROWS+1], int columnIndex[NNZ],
          DTYPE values[NNZ], DTYPE y[SIZE], DTYPE x[SIZE]);

#endif // __MATRIXMUL_H__ not defined

test_beach

#include "spmv.h"
#include 

void matrixvector(DTYPE A[SIZE][SIZE], DTYPE *y, DTYPE *x)
{
    for (int i = 0; i < SIZE; i++) {
        DTYPE y0 = 0;
        for (int j = 0; j < SIZE; j++)
            y0 += A[i][j] * x[j];
        y[i] = y0;
    }
}

int main(){
    int fail = 0;
    DTYPE M[SIZE][SIZE] = {{3,4,0,0},{0,5,9,0},{2,0,3,1},{0,4,0,6}};
    DTYPE x[SIZE] = {1,2,3,4};
    DTYPE y_sw[SIZE];
    DTYPE values[] = {3,4,5,9,2,3,1,4,6};
    int columnIndex[] = {0,1,1,2,0,2,3,1,3};
    int rowPtr[] = {0,2,4,7,9};
    DTYPE y[SIZE];

    spmv(rowPtr, columnIndex, values, y, x);
    matrixvector(M, y_sw, x);

    for(int i = 0; i < SIZE; i++)
        if(y_sw[i] != y[i])
            fail = 1;

    if(fail == 1)
        printf("FAILED\n");
    else
        printf("PASS\n");

    return fail;
}

循环的优化与数组的分块

#include "spmv.h"

const static int S = 7;

void spmv(int rowPtr[NUM_ROWS+1], int columnIndex[NNZ],
          DTYPE values[NNZ], DTYPE y[SIZE], DTYPE x[SIZE])
{
  L1: for (int i = 0; i < NUM_ROWS; i++) {
      DTYPE y0 = 0;
    L2_1: for (int k = rowPtr[i]; k < rowPtr[i+1]; k += S) {
#pragma HLS pipeline II=S
          DTYPE yt = values[k] * x[columnIndex[k]];
      L2_2: for(int j = 1; j < S; j++) {
              if(k+j < rowPtr[i+1]) {
                  yt += values[k+j] * x[columnIndex[k+j]];
              }
          }
          y0 += yt;
      }
    y[i] = y0;
  }
}