Python 中的图：Dijkstra 算法

介绍

  图是最有用的数据结构之一。它们可用于对几乎所有事物进行建模——对象关系和网络是最常见的。图像可以表示为网格状的像素图，句子可以表示为单词的图。图表被用于各个领域，从制图到社会心理学，当然它们在计算机科学中也被广泛使用。因此图搜索和遍历起着重要的计算作用。Dijkstra 算法旨在找到 图中节点 之间的最短路径。它是由荷兰计算机科学家 Edsger Wybe Dijkstra 于 1956 年在思考从鹿特丹到格罗宁根的最短路线时设计的。Dijkstra 算法 多年来一直在发生变化，并且存在各种版本和变体。最初用于计算两个节点之间的最短路径。由于它的工作方式 ，适用于计算起始节点和图中每个其他节点之间的最短路径。这种方式可用于生成 最短路径树，该树由两个节点以及所有其他节点之间的最短路径组成。然后你可以修剪掉你不感兴趣的树，得到两个节点之间的最短路径，但你不可避免地必须计算整个树，这是 Dijkstra 算法 的一个缺点，它不适合大型图。

Dijkstra 算法

  Dijkstra 算法 适用于无向、连接、加权图，Dijkstra 算法 可以求出源节点到其他所有节点的最短路径。
  一开始，我们要创建一组已访问顶点，以跟踪所有已分配正确最短路径的顶点。我们还需要设置图中所有顶点的“成本”（通向它的当前最短路径的长度）。开始时所有成本都将设置为 “无穷大(inf)” ，以确保我们可以与之比较的所有其他成本都小于起始成本。唯一的例外是第一个起始顶点的成本——这个顶点的成本为 0，因为它没有通往自身的路径——标记为 源节点 s。然后依据以下三个规则，直到遍历整个图：

• 每次从未标记的节点中选择距离出发点最近的节点，标记，收录到最优路径集合中。
• 对于当前节点 n 和其的邻居节点 m 如果 cheapestPath(s, n) + cheapestPath(n, m) < cheapestPath(s, m)，则更新 s 到 m 的最短路径为 cheapestPath(s, n) + cheapestPath(n, m)。
• 且每次更新最短路径时会保存该节点的前节点。

下面用一个无向、加权、连通图来解释上述规则原理：

假设 Vertex 0 为起点(源节点)。我们将把图中顶点的初始成本设置为无穷大，除了起始顶点：

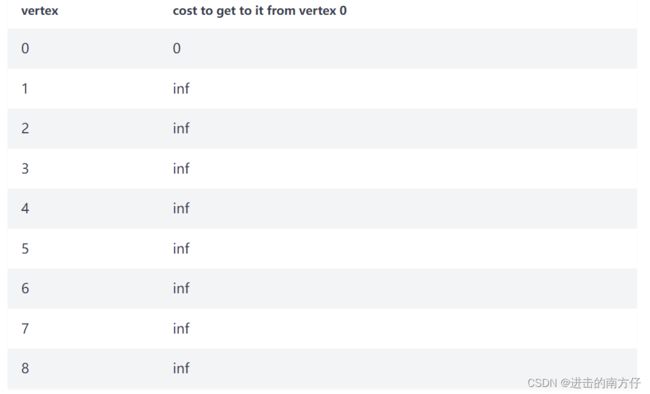
我们选择成本最低的顶点——即 Vertex 0。我们将其标记为已访问并将其添加到我们的已访问顶点集。起始节点将始终具有最低成本，因此它将始终是第一个添加的节点，同时标记 Vertex 0，之后不用再进行访问：

然后，我们将更新相邻顶点（1 和 6）的成本。由于 0 + 4 < infinity 和 0 + 7 < infinity，我们更新这些顶点的成本：

现在我们访问未标记顶点中的最小成本顶点。4 < 7，所以我们遍历到 Vertex 1：

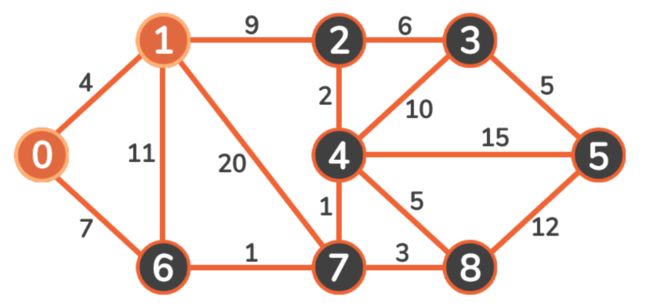
在遍历时，我们将其标记为已访问，然后观察并更新相邻顶点：2、6 和 7：

• 因为 4 + 9 < infinity，Vertex 2 的新成本将是 13。
• 因为 4 + 11 > 7，Vertex 6 的成本将保持为 7。
• 因为 4 + 20 < infinity，Vertex 7 的新成本将是 24。

则新成本如下：

此时在未标记的顶点中 Vertex 6的成本最小，因此将其作为出发点，将其标记为已访问并更新其相邻顶点的成本：

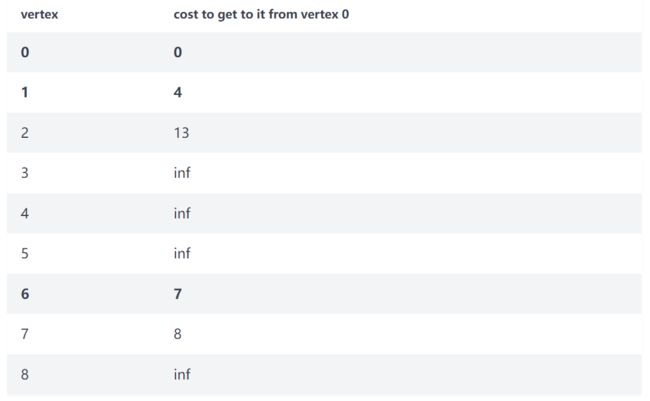
该过程继续到 Vertex 7：


再一次，到 Vertex 4：


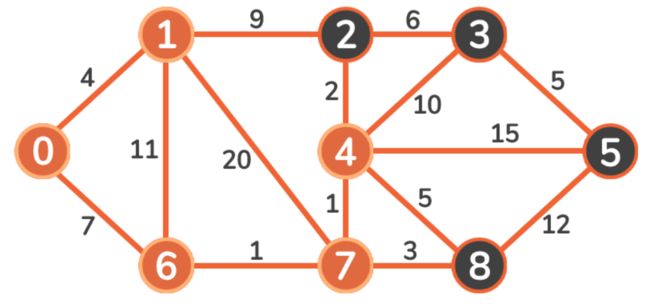
再一次，到 Vertex 2：

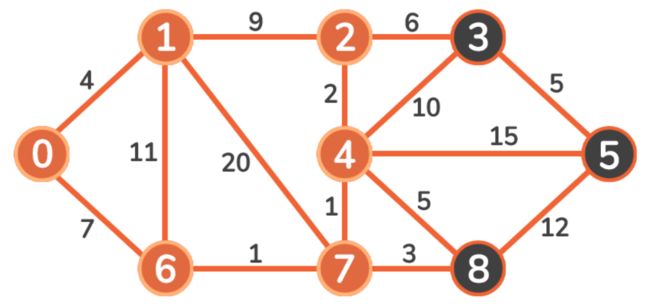
我们要考虑的唯一顶点是 Vertex 3。由于11 + 6 < 19，Vertex 3 的成本被更新。然后继续到 Vertex 8。

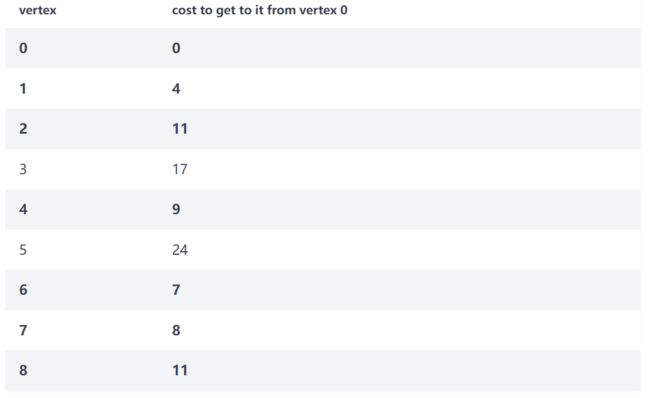
然后更新 Vertex 3：

最后更新 Vertex 5：

没有更多未访问的顶点可能需要更新。我们的最终成本表示从节点 0 到图中每个其他节点的最短路径：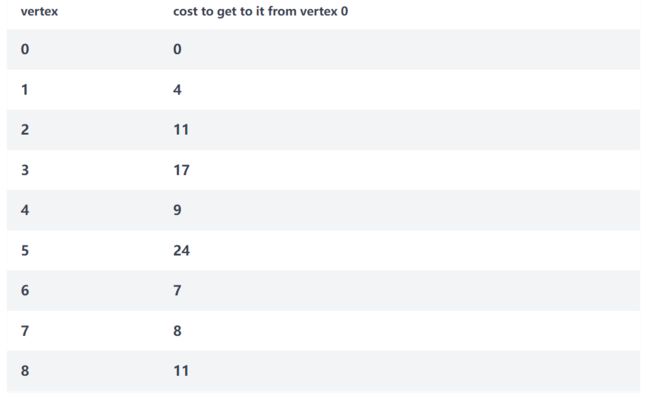
动画演示如下：来自 https://www.youtube.com/watch?v=JLARzu7coEs

Python 实现 Dijkstra 算法

为了对我们还没有访问过的顶点进行排序和跟踪——我们将使用 PriorityQueue(优先队列)：

from queue import PriorityQueue

实现一个名为 Graph 的类的构造函数：

class Graph:
    def __init__(self, num_of_vertices):
        self.vertices = num_of_vertices
        #距离表
        self.edges = [[-1 for i in range(num_of_vertices)] for j in range(num_of_vertices)]
        #记录被访问过的节点
        self.visited = []

在这个简单的参数化构造函数中，将图中顶点的数量作为参数，并初始化了三个字段：

• vertices：表示图中的顶点数。
• edges：以矩阵的形式表示边的列表。对于节点 u 和 v，self.edges[u][v] = weight。
• visited：将包含访问的顶点的集合。

定义一个将向图形添加边的方法：

    def add_edge(self, u, v, weight):
        #记录u，v两节点之间的距离
        #要注意的是如果是有向图只需定义单向的权重
        #如果是无向图则需定义双向权重
        self.edges[u][v] = weight
        self.edges[v][u] = weight

定义 Dijkstra 算法：

    def dijkstra(self, start_vertex):
        #开始时定义源节点到其他所有节点的距离为无穷大
        D = {v: float('inf') for v in range(self.vertices)}
        #源节点到自己的距离为0
        D[start_vertex] = 0
        #优先队列
        pq = PriorityQueue()
        pq.put((0, start_vertex))
        # 记录每个节点的前节点，便于回溯
        previousVertex = {}

        while not pq.empty():
            #得到优先级最高的节点，也就是前节点到其他节点距离最短的节点作为当前出发节点
            (dist, current_vertex) = pq.get()
            #标记已访问过的节点(最有路径集合)
            self.visited.append(current_vertex)

            for neighbor in range(self.vertices):
                #邻居节点之间距离不能为-1
                if self.edges[current_vertex][neighbor] != -1:
                    distance = self.edges[current_vertex][neighbor]
                    #已经访问过的节点不能再次被访问
                    if neighbor not in self.visited:
                        #更新源节点到其他节点的最短路径
                        old_cost = D[neighbor]
                        new_cost = D[current_vertex] + distance
                        if new_cost < old_cost:
                            #加入优先队列
                            pq.put((new_cost, neighbor))
                            D[neighbor] = new_cost
                            previousVertex[neighbor] = current_vertex
        return D, previousVertex

在这段代码中，首先创建了一个大小为 num_of_vertices 的字典 D，用于统计最短路径的成本。整个列表初始化为无穷大。这将是一个列表，我们在其中保留从 start_vertex 所有其他节点的最短路径。我们将起始顶点的值设置为 0，因为这是它与自身的距离。然后，我们初始化一个优先级队列，我们​​将使用它来快速将顶点从最远到最远排序。我们将起始顶点放入优先级队列中。再然后初始化previousVertex ，用于标记每个节点的前节点。现在，对于优先队列中的每个顶点，我们将首先将它们标记为已访问，然后我们将遍历它们的邻居。如果邻居没有被访问，我们将比较它的旧成本和新成本。旧代价是从起始顶点到邻居的最短路径的当前值，而新代价是从起始顶点到当前顶点的最短路径与当前顶点到相邻顶点的距离之和的值邻居。如果新成本低于旧成本，我们将邻居及其成本放入优先级队列，并相应地更新我们保留最短路径的列表，同时更新邻居节点的前节点。最后，在所有顶点都被访问并且优先级队列为空之后，我们返回字典 D 和 previousVertex 。

实现之前的例子：

def Dijkstra() :
    g = Graph(9)
    g.add_edge(0, 1, 4)
    g.add_edge(0, 6, 7)
    g.add_edge(1, 6, 11)
    g.add_edge(1, 7, 20)
    g.add_edge(1, 2, 9)
    g.add_edge(2, 3, 6)
    g.add_edge(2, 4, 2)
    g.add_edge(3, 4, 10)
    g.add_edge(3, 5, 5)
    g.add_edge(4, 5, 15)
    g.add_edge(4, 7, 1)
    g.add_edge(4, 8, 5)
    g.add_edge(5, 8, 12)
    g.add_edge(6, 7, 1)
    g.add_edge(7, 8, 3)

    D, previousVertex = g.dijkstra(0)
    #每个节点的前节点，可通过回溯得到最短路径
    print(previousVertex)
    for vertex in range(len(D)):
        print(f"distance from vertex {0} to vertex {vertex} is {D[vertex]}")

结果：

测试

得到节点s和t之间的最短路径。

上图是一个有向图，而我们在第一个例子中定义的是无向图，因此要修改代码。在代码中与无向图的差异只是一行，即定义权重时只定义一边，只需注释掉 self.edges[v][u] = weight 即可。为了实现方便，图中节点的名称并未使用字符表示，而是使用数字进行表示，在搜索完之后根据字典再对应回去。

from queue import PriorityQueue

class Graph:
    def __init__(self, num_of_vertices):
        self.vertices = num_of_vertices
        #距离表
        self.edges = [[-1 for i in range(num_of_vertices)] for j in range(num_of_vertices)]
        #记录被访问过的节点
        self.visited = []

    def add_edge(self, u, v, weight):
        #记录u，v两节点之间的距离
        #要注意的是如果是有向图只需定义单向的权重
        #如果是无向图则需定义双向权重
        self.edges[u][v] = weight
        # self.edges[v][u] = weight

    def dijkstra(self, start_vertex):
        #开始时定义源节点到其他所有节点的距离为无穷大
        D = {v: float('inf') for v in range(self.vertices)}
        #源节点到自己的距离为0
        D[start_vertex] = 0
        #优先队列
        pq = PriorityQueue()
        pq.put((0, start_vertex))
        # 记录每个节点的前节点，便于回溯
        previousVertex = {}

        while not pq.empty():
            #得到优先级最高的节点，也就是前节点到其他节点距离最短的节点作为当前出发节点
            (dist, current_vertex) = pq.get()
            #标记已访问过的节点(最有路径集合)
            self.visited.append(current_vertex)

            for neighbor in range(self.vertices):
                #邻居节点之间距离不能为-1
                if self.edges[current_vertex][neighbor] != -1:
                    distance = self.edges[current_vertex][neighbor]
                    #已经访问过的节点不能再次被访问
                    if neighbor not in self.visited:
                        #更新源节点到其他节点的最短路径
                        old_cost = D[neighbor]
                        new_cost = D[current_vertex] + distance
                        if new_cost < old_cost:
                            #加入优先队列
                            pq.put((new_cost, neighbor))
                            D[neighbor] = new_cost
                            previousVertex[neighbor] = current_vertex
        return D, previousVertex

def Dijkstra():
    g = Graph(6)
    g.add_edge(0, 1, 6)
    g.add_edge(0, 3, 3)
    g.add_edge(0, 2, 5)
    g.add_edge(1, 4, 3)
    g.add_edge(1, 3, 1)
    g.add_edge(2, 3, 1)
    g.add_edge(2, 5, 2)
    g.add_edge(3, 4, 7)
    g.add_edge(3, 5, 9)
    g.add_edge(5, 4, 5)

    D, previousVertex = g.dijkstra(0)
    # print(previousVertex)

    #节点名字与数字的对应表
    dic = {0 : 's', 1 : 'v', 2 : 'u', 3 : 'w', 4 : 't', 5 : 'z'}
    path = []
    cheapest_path = []
    key = 4
    #回溯，得到源节点到目标节点的最佳路径
    while True:
        if key == 0 :
            path.append(0)
            break
        else :
            path.append(key)
            key = previousVertex[key]
    #节点名字由数字转成字符
    for point in path[ : : -1] :
        cheapest_path.append(dic[point])
    cheapest_path = "->".join(cheapest_path)

    print(f"distance from vertex {dic[0]} to vertex {dic[4]} is {D[4]},"
            f"the cheapest path is {cheapest_path}")


if __name__ == '__main__':
    Dijkstra()

结果：