Pyts入门之时间序列的分类---理解LearningShapelets算法(四)
简介
本章节直接跳过了BOSSVS算法,因为BOSSVS和SAX-VSM的区别也就只在于前面数据预处理的方式了,SAX-VSM用的是分箱的字词转换,而BOSSVS用的是Symbolic Fourier Approximation(详见第一节,本文不再赘述)也就是使用傅里叶变换的提取特征方法,所以与其介绍一遍差不多的,不如留给读者自行探索。
那么本节我将给各位介绍pyts中的LearningShapelets算法,来自于14年的“Learning Time-Series Shapelets”这篇文章,本算法过程简单,具体的实现过于复杂(这个时候就感受到了有别人帮你写好直接调用是多么惬意的事情),主要分为以下两步:
1.计算shapelets和时间序列之间的距离。
2.以logistic回归的方式将shapelets作为系数来进行拟合,目的是减小距离。
这里涉及到了一个概念:shapelets。
我个人觉得翻译为子特征比较好,啥叫子特征呢,就像下面这样:
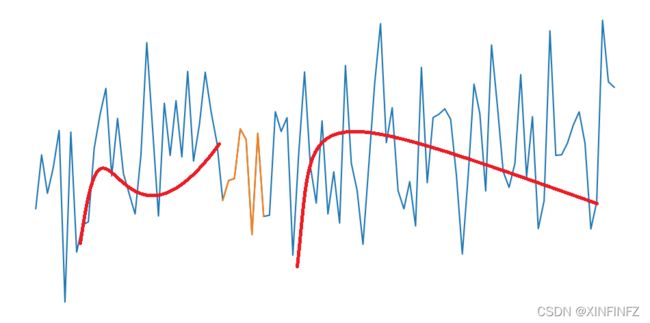
上图中黄线为子序列,红线为子特征,实际上子特征的意思就是以一段曲线来表示原有序列的总体特征,这段曲线可以很长,来表示一大段特征(但不精确,如右边曲线),也可以很短,来表示关键特征(抓住重点,如左边曲线),当我们找到了足够好的shapelets,就可以轻松对时间序列进行分类(比如区分两种树叶只要看到其中一种树叶的其中一小段一定具有锯齿即可)。
理解了之后,这样也引出了三个问题:
1.子特征怎么选取?怎么产生??
2.距离是怎么计算的?
3.我们怎么去预测新的序列?
PS:在进入接下来的api介绍之前,我希望读者能够自行思考一下这几个问题,这几天没动笔的原因其实也是我的初衷是以一种让人更容易理解的方式去学算法,同时把API文档以自己的理解翻译一遍,而之前的文章好像过于深奥了一点,深扒源码就没意思了。
API介绍
class pyts.classification.LearningShapelets
(n_shapelets_per_size=0.2, min_shapelet_length=0.1,
shapelet_scale=3, penalty='l2', tol=0.001, C=1000,
learning_rate=1.0, max_iter=1000, multi_class='multinomial',
alpha=-100, fit_intercept=True, intercept_scaling=1.0, class_weight=None,
verbose=0, random_state=None, n_jobs=None)
以上是默认参数,参数的详细说明如下:
| 参数 | 说明 |
|---|---|
| n_shapelets_per_size | 每一种size,会有多少个shapelets,如果为float型,那么等于n_shapelets_per_size * n_timestamps(时间序列长度)并向上取整 |
| min_shapelet_length | shapelets的最小长度,为float型则等于min_shapelet_length * n_timestamps并向上取整 |
| shapelet_scale | shapelets的变化尺度(int型),shaplets的长度等于min_shapelet_length * np.arange(1, shapelet_scale + 1)。shapelets的总共数目=n_shapelets_per_size * shapelet_scale。注:此处np.arange表示步长为1从1开始到shaplet_scale+1的序列。 |
| penalty | ‘l1’或者’l2’,正则化的两种法则 |
| tol | float,停止迭代的容忍度,具体表现为“if abs(losses[-2] - losses[-1]) < self.tol * losses[-1]:break“,即容忍度越高,停止迭代越快 |
| C | 必须是正的float型,越小正则化惩罚力度越大 |
| learning_rate | float,梯度下降的学习率,如果loss不再下降学习率会自动下降 |
| max_iter | int,最大迭代次数 |
| multi_class | 可选{‘multinomial’, ‘ovr’, ‘ovo’},multinominal为默认,表示多项式交叉熵,ovr为one-vs-rest,ovo为one-vs-one,ovr和ovo的区别详见点击这里 |
| alpha | float,越小softmin函数的下界越精准,标准时间序列用默认值即可 |
| fit_intercept | True or False,决策函数是否添加常量 |
| intercept_scaling | float,多了一个常量的合成特征,只有fit_intercept为True时使用 |
| class_weight | None or ‘balanced’ ,类别权重,默认不添加,balanced会添加一个n_samples / (n_classes * np.bincount(y))的权重 |
| verbose | int,正数打印每次迭代的loss |
| random_state | None, int or RandomState instance,伪随机种子生成器。不同int表示不同种子,若为RandomState则随机种子 |
| n_jobs | None or int,计算并行,只有multi_class为ovr或ovo才会生效 |
示例和重点问题讲解
先来理解一下API里的前三个参数,至于其他参数基本都是sklearn的logistic regression里自带的,没什么好说的。
from pyts.classification import LearningShapelets
X = [[1, 2, 2, 1, 2, 3, 2],
[0, 2, 0, 2, 0, 2, 3],
[0, 1, 2, 2, 1, 2, 2]]
y = [0, 1, 0]
clf = LearningShapelets(random_state=42, tol=0.01)
clf.fit(X, y)
官网示例,X三行七列,表示n_timestamps=7,Y是标签列,这里只有0,1两个标签,所以是二分类问题,拟合完毕之后打印如下参数:
clf.shapelets_ #打印得到的shapelets

可以发现总共有6个shapelets,其中包含一个数字的数组有两个,两个数字的也有两个,三个数字的也有两个。这是为啥呢?
解:因为n_timestamps=7,所以n_shapelets_per_size=默认0.2 * n_timestamps=1.4向上取整得到两个,也就是每种size的数组有两个。
同时min_shapelet_length=默认0.1*n_timestamps=0.7向上取整得到1,也就是数组的最小起始长度是1,所以从数组从1个数字开始。
而shapelet_scale = min_shapelet_length * np.arange(1, 默认3 + 1),也就是

所以数组从1个数字开始变化到3个数字结束。
那么shapelets是怎么选取和产生的呢?
解:先通过K-means无监督学习找到一定数目的质心,再通过梯度下降选取loss最小的shapelets。
有了拟合好的分类器,我们就可以通过clf.predict方法去轻松预测新的时间序列,那这个过程的实质是什么呢?
解:我们训练好的逻辑回归分类器实际上是一组在学习shaplelets的特征时得到的权重(weights),我们可以按以下方法打印出来:
print(clf.coef_[0])
print(clf.intercept_)

权重包含coef(系数)和intercept_(常量两部分),那么当新的时间序列到来时,只需要计算该时间序列和shaplets的distance(距离),然后再乘以权重就可以得到我们的决策函数值,也就是源代码中写的:
X_decision = np.squeeze(distance @ weights) #@其实就是矩阵乘向量,和np.dot一样
那么distance如何求呢,这里其实稍微有点复杂,先讲一下pyts.utils.windowed_view(X, window_size, window_step=1)这个函数,它包含三个参数:输入数据,窗口长度,窗口步长,像刚刚我们的数据用这个进行变换就是:

你可以发现第二列实际上就是第一列表示的时间序列往前滑动了一格,也就是说在算距离的时候用的是滑动了窗口的多条序列去减去shapelets的均值,从直觉上理解,就是用时间序列的不同部分去分别和得到的shapelets序列比较。
后记
去将一个复杂的算法转换成易懂的文字是非常难的一件事情,同时还包含了翻译API的任务,几次动笔却又几次放下,可以的话以后希望能在github上上传我的notebook并出版个小册子,现在是纯纯的为爱发电了。