图机器学习——5.2 图神经网络:GNN的构建与训练
1. GNN的构建
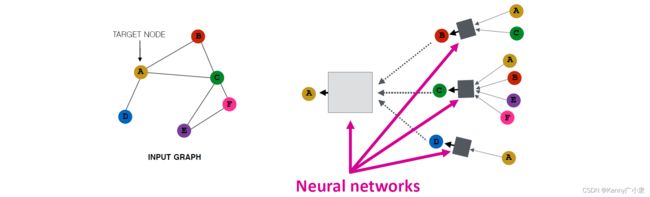
我们将节点的邻居定义为可计算的图,图神经网络的主要想法是:每一个节点可以从周围的邻居中汇聚信息,而这个汇聚的方式就是通过神经网络来进行。以下图为例,我们来进行解释:
首先以节点A为目标节点,其邻居为B, C, D,那么A的信息就由B, C, D进行汇聚;接着进行递归,B的信息来源于A, C(由于是无向图,因此A也需要进行考虑,下面类似);C的信息来源于A, B, E, F;D又来源于A。因此得到上右图所示的网络。
接着我们考虑所有的节点,均作为目标节点,构建一个这样的传递模型。
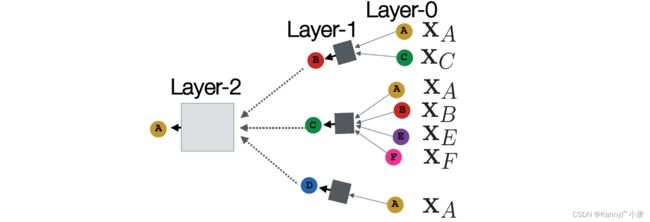
这种传递模型可以为任意深度,且有如下几个性质:
- 节点在每一层都有嵌入(embedding);
- 节点 v v v 的第 0 层的嵌入是其输入特征, x v x_{v} xv;
- 第 k k k层的嵌入从 k k k 的邻居节点( k − 1 k-1 k−1层)获取信息。
下面详细考虑每一层中具体的网络结构与更新迭代公式。
h v ( k + 1 ) = σ ( W k ∑ u ∈ N ( v ) h u ( k ) ∣ N ( v ) ∣ + B k h v ( k ) ) , ∀ k ∈ { 0 , … , K − 1 } \mathrm{h}_{v}^{(k+1)}=\sigma\left(\mathrm{W}_{k} \sum_{u \in \mathrm{N}(v)} \frac{\mathrm{h}_{u}^{(k)}}{|\mathrm{N}(v)|}+\mathrm{B}_{k} \mathrm{h}_{v}^{(k)}\right), \forall k \in\{0, \ldots, K-1\} hv(k+1)=σ⎝⎛Wku∈N(v)∑∣N(v)∣hu(k)+Bkhv(k)⎠⎞,∀k∈{0,…,K−1}
初始层为节点的输入特征: h v 0 = x v \mathrm{h}_{v}^{0}=\mathrm{x}_{v} hv0=xv,最后一层为得到的嵌入结果: z v = h v ( K ) \mathrm{z}_{v}=\mathrm{h}_{v}^{(K)} zv=hv(K)。迭代公式中的 σ \sigma σ为非线性激活函数(如,ReLU);激活函数中间的两部分分别为:上一层的邻域节点嵌入的平均值乘以一个可训练的权重 W k \mathrm{W}_{k} Wk;以及上一轮迭代中当前节点的嵌入 h v ( k ) \mathrm{h}_{v}^{(k)} hv(k)乘以可训练的权重 B k \mathrm{B}_{k} Bk。
令 H ( k ) = [ h 1 ( k ) … h ∣ V ∣ ( k ) ] T H^{(k)}=\left[\begin{array}{lll}h_{1}^{(k)} & \ldots h_{|V|}^{(k)}\end{array}\right]^{\mathrm{T}} H(k)=[h1(k)…h∣V∣(k)]T ,则有 ∑ u ∈ N v h u ( k ) = A v , : H ( k ) \sum_{u \in N_{v}} h_{u}^{(k)}=A_{v,:} \mathrm{H}^{(k)} ∑u∈Nvhu(k)=Av,:H(k),其中, A v , : A_{v,:} Av,:为邻接矩阵 A A A的第 v v v行。再构造一个对角度矩阵 D D D,其中 D v , v = Deg ( v ) = ∣ N ( v ) ∣ D_{v, v}=\operatorname{Deg}(v)=|N(v)| Dv,v=Deg(v)=∣N(v)∣,其逆 D − 1 D^{-1} D−1可以表示为: D v , v = Deg ( v ) = ∣ N ( v ) ∣ D_{v, v}=\operatorname{Deg}(v)=|N(v)| Dv,v=Deg(v)=∣N(v)∣。则前面的迭代公式邻居节点的传递项可以表示为矩阵形式:
∑ u ∈ N ( v ) h u ( k − 1 ) ∣ N ( v ) ∣ ⇒ H ( k + 1 ) = D − 1 A H ( k ) \sum_{u \in N(v)} \frac{h_{u}^{(k-1)}}{|N(v)|} \Rightarrow H^{(k+1)}=D^{-1} A H^{(k)} u∈N(v)∑∣N(v)∣hu(k−1)⇒H(k+1)=D−1AH(k)
最终的矩阵形式的迭代公式为:
H ( k + 1 ) = σ ( A ~ H ( k ) W k T + H ( k ) B k T ) H^{(k+1)}=\sigma\left(\textcolor{red}{\tilde{A} H^{(k)} W_{k}^{\mathrm{T}}}+\textcolor{blue}{H^{(k)} B_{k}^{\mathrm{T}}}\right) H(k+1)=σ(A~H(k)WkT+H(k)BkT)
其中, A ~ = D − 1 A \tilde{A}=D^{-1} A A~=D−1A,红蓝两种颜色的公式分别对应邻居节点的信息传递,以及自己信息的传递,如下图:
2. GNN的训练
深度学习的训练依赖于损失函数梯度的反向传播,GNN也一样,但其有两种损失,有监督损失(利用节点的标签)与无监督损失(利用图的结构)。
- 有监督损失就是传统的方式:
min Θ L ( y , f ( z v ) ) \min _{\Theta} \mathcal{L}\left(\boldsymbol{y}, f\left(\boldsymbol{z}_{v}\right)\right) ΘminL(y,f(zv))
其中, y \boldsymbol{y} y为节点的标签, f ( z v ) f\left(\boldsymbol{z}_{v}\right) f(zv)表示对最后得到的嵌入结果再套一个函数,如sigmoid,softmax函数等。 L \mathcal{L} L可以为L2损失,交叉熵损失等。
- 无监督损失则为嵌入的训练方式:
L = ∑ z u , z v CE ( y u , v , DEC ( z u , z v ) ) \mathcal{L}=\sum_{z_{u}, z_{v}} \operatorname{CE}\left(y_{u, v}, \operatorname{DEC}\left(z_{u}, z_{v}\right)\right) L=zu,zv∑CE(yu,v,DEC(zu,zv))
当两个节点 u , v u,v u,v之间有边连接,则对应 y u , v = 1 y_{u, v}=1 yu,v=1,表示两个节点非常相似。CE为交叉熵,DEC为解码结构,可以是内积,或者双曲空间的距离函数。其实就是前面学习过的嵌入算法。这里列举出一个分类问题的损失函数(交叉熵损失函数)具体构造:
L = ∑ v ∈ V y v log ( σ ( z v T θ ) ) + ( 1 − y v ) log ( 1 − σ ( z v T θ ) ) \mathcal{L}=\sum_{v \in V} y_{v} \log \left(\sigma\left(\mathrm{z}_{v}^{\mathrm{T}} \theta\right)\right)+\left(1-y_{v}\right) \log \left(1-\sigma\left(\mathrm{z}_{v}^{\mathrm{T}} \theta\right)\right) L=v∈V∑yvlog(σ(zvTθ))+(1−yv)log(1−σ(zvTθ))
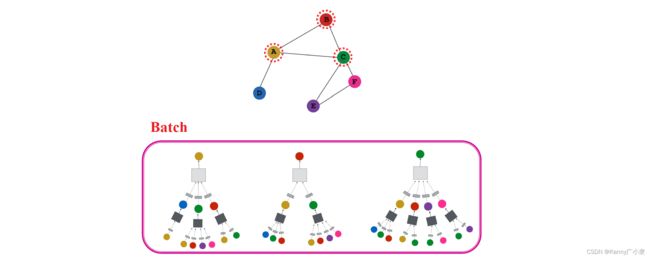
其中, z v \mathrm{z}_{v} zv为最后一层的嵌入结果, θ \theta θ为分类权重, σ \sigma σ为最后分类的激活函数, y v y_{v} yv为真实的标签。训练时,每一层的权重都进行共享。图神经网络中的batch是一系列节点的集合,如下图所示:
最终一些节点我们可能从未训练到,但由于我们是共享每一层的权重值,因此也能够得到最终的嵌入结果:
因此模型具有很强的泛化能力,并且可以预测新的节点。