【强化学习纲要】学习笔记之Markov Decision Processes

【强化学习纲要】学习笔记系列

---

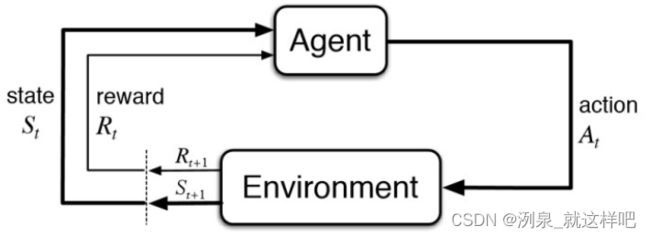
Markov Chain → Markov Reward Process（MRP）→ Markov Decision Processes（MDP）

MDP基本假设：环境是完全可观测的

• MDP可以用于处理最优控制问题，根据环境确定出最佳控制策略
• 部分可观测的问题可以转化为MDP

Markov Process

未来状态依赖于给定的历史状态

• 历史状态：$h_t=\{s_1,s_2,\dots ,s_t\}$
• 状态转移：$p(s_{t+1}|s_t)=p(s_{t+1}|h_t)$, $p(s_{t+1}|s_t,a_t)=p(s_{t+1}|h_t,a_t)$
• 状态转移矩阵
  

Markov Reward(MRPs)

• MRP = Markov Chain + reward
• reward function $R(s_t=s)=\mathbb{E}[r_t|s_t=s]$
• Discouted sum of reward: $G_t=R_{t+1}+\gamma R_{t+2}+\cdots +{\gamma }^{T-t-1}{R}_T$
• value funciton $V_t(s)=\mathbb{E}[G_t|s_t=s]=\mathbb{E}[R_{t+1}+\gamma R_{t+2}+\cdots +{\gamma }^{T-t-1}{R}_T|s_t=s]$

其中$\gamma$即为折扣因子(Discout factor), 作用包括：

• 避免循环Markov processes的无限return（迭代到一定长度，$\gamma$作用下数值极小）
• 表征未来的不确定性
• 体现出及时反馈和延迟反馈的差异性，agent普遍倾向于及时反馈（生物本性贪婪和没耐心）
• 当$\gamma =0$，只考虑及时反馈，当$\gamma =1$，延迟反馈的价值等同于及时反馈

MRP的value function满足Bellman equation：
$$V(s)=R(s)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s)V(s^{\prime })$$
其中右边两项分别是及时反馈和未来反馈，未来反馈是状态发生概率与对应状态的value的乘积之和
对于N个状态，可以写成局长表达式：
$V=R+\gamma PV$
由此，当系统收敛时，即状态不再发生变化，可以得到MRP的解：
$$V=(I-\gamma P{)}^{-1}R$$
方程求解是$O(N^3)$复杂度，只适合于N较小的时候，即状态数少的问题
更常用的做法是迭代求解：

• 动态规划（Dynamic Programming）
• Monte-Carlo evaluation
  
• Iterative Algorithm（policy iteration and value iteration，Temporal-Difference learning）
  

Markov Decision Processes(MDPs)

MDP = MRP + decision
在MRP基础上考虑policy
$$R(s_t=s,a_t=a)=\mathbb{E}[r_t|s_t=s,a_t=a]$$

policy in MDP

• Policy: 在特定state下所采取的action
  $$\pi (a|s)=P(a_t=a|s_t=s)$$

• Policy 是稳定的，时间独立，也就是不管时间变化，特定状态对应特定policy

• Bellman Expectation Equation for value function
  $$v^{\pi }(s)=\sum _{a\in A}\pi (a|s)(R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)v^{\pi }(s^{\prime }))$$
  其中，$v^{\pi }(s)$用于评估在给定state-action的映射之后，当前state的value，
  外层$\sum$是指所有action，$R(s,a)$是当前reward，内层$\sum$是指特定action导致的未来状态的概率和value的乘积，也就是未来reward

• Bellman Expectation Equation for Q-function
  $$q^{\pi }(s,a)=R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)\sum _{a^{\prime }\in A}\pi (a^{\prime }|s^{\prime })q^{\pi }(s^{\prime },a^{\prime })$$
  其中， Q-function的$q^{\pi }(s,a)$用于评估给定state采取某个action的value，$R(s,a)$是指当前reward，外层$\sum$是每个action到新状态s’的转移概率与对应reward乘积之和，内层$\sum$是未来state-action概率和action对应value的乘积之和

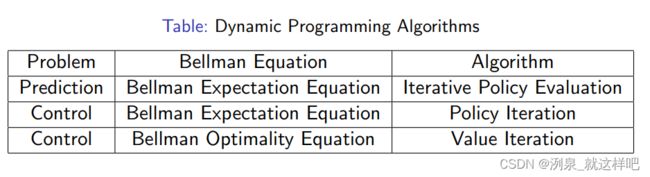
预测和控制

预测是输出$v^{\pi }$
控制是输出最佳的value function $v^{\ast }$和最佳policy$v^{\ast }$
预测和控制都可以由动态规划求解
动态规划的特性：

• 系统可分解为最佳子结构：状态
• 最佳子结构之间可以多次递归：状态转移

Policy evaluation in MDP

• objective： 评估给定policy $\pi$
• 输出：给定policy下的value function $v^{\pi }$
• 基于Bellman expectation进行迭代直至收敛
  $$v^{\pi }(s)=\sum _{a\in A}\pi (a|s)(R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)v^{\pi }(s^{\prime }))$$

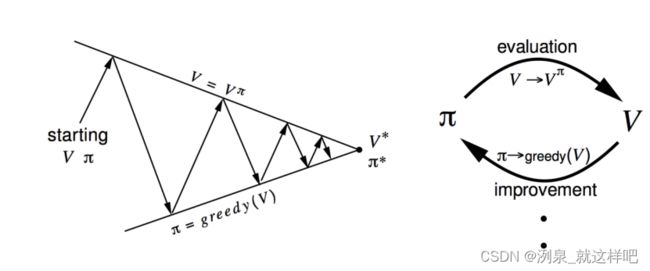
Policy iteration

• policy iteration = policy evaluation + policy improvement
  $${\pi }^{\prime }=greedy(v^{\pi })$$
  根据收敛的$v^{\pi }$得到当前最佳的policy
  往复迭代 policy evaluation 和 policy improvement，直到二者不发生变化
  （据理论证明，policy性能是单调提升的）
  

Value Iteration

• objective: 找到最佳的policy
• solution：使用Bellman optimality equation

$$q_{k+1}(s,a)=R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)v_k(s^{\prime })$$
v_{k+1}(s) = max_a q_{k+1}(s,a)

对于子问题，如果我们总能得到最佳state及value function，那么可以直接对value function进行迭代
$$v(s)=\underset{a\in A}{\max }\left(R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s|s,a)v(s^{\prime })\right)$$

当值迭代完成，则只需要选择最优策略即可
$$\pi (s)=\arg \underset{a}{\max }R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)v_{k+1}(s^{\prime })$$

Policy Iteration vs Value Iteration

• Policy iteration： 包含policy evaluation和policy improvement两个步骤往复迭代直到收敛
• Value iteration：只需要找到最优的value function + one policy extraction
• value iteration相当于融合了policy iteration的两个过程，每次迭代就已经要求找到最佳policy来得到当前最佳value；而policy iteration只是给定policy去确定value（非最佳），然后基于value优化policy，再去确定value

同步动态规划的缺点

• 需要知道状态全集
• 当全集特别大，则迭代次数非常大
• 不同状态之间的更新速度不一样