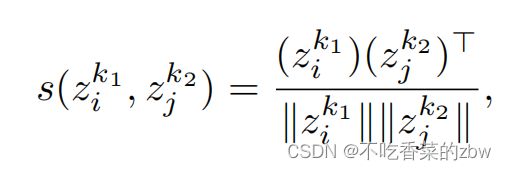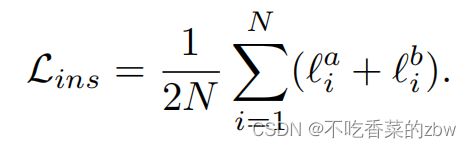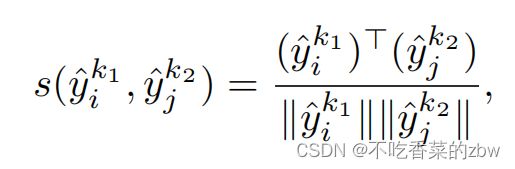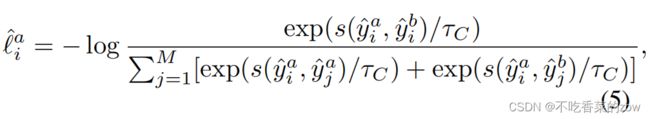论文阅读“Contrastive clustering”（AAAI2021）

论文标题

 

Contrastive clustering

论文作者、链接

作者：Li, Yunfan and Hu, Peng and Liu, Zitao and Peng, Dezhong and Zhou, Joey Tianyi and Peng, Xi

链接：Contrastive Clustering| Proceedings of the AAAI Conference on Artificial Intelligence

代码：GitHub - Yunfan-Li/Contrastive-Clustering: Code for the paper "Contrastive Clustering" (AAAI 2021)

---

Introduction逻辑（论文动机&现有工作存在的问题）

聚类——往往在真实世界的数据集中，计算消耗是非常大的——深度聚类通过使用神经网络来提取对下游任务有用的图片的特征信息——现在注重于如何学习特征表达，以及端到端方式的进行聚类——两阶段方式交替学习的过程中（特征学习阶段和聚类阶段），会累积误差——两阶段的方法只能处理离线任务（即，是基于整个数据集的聚类，在大尺度数据集上难以适用）

论文核心创新点

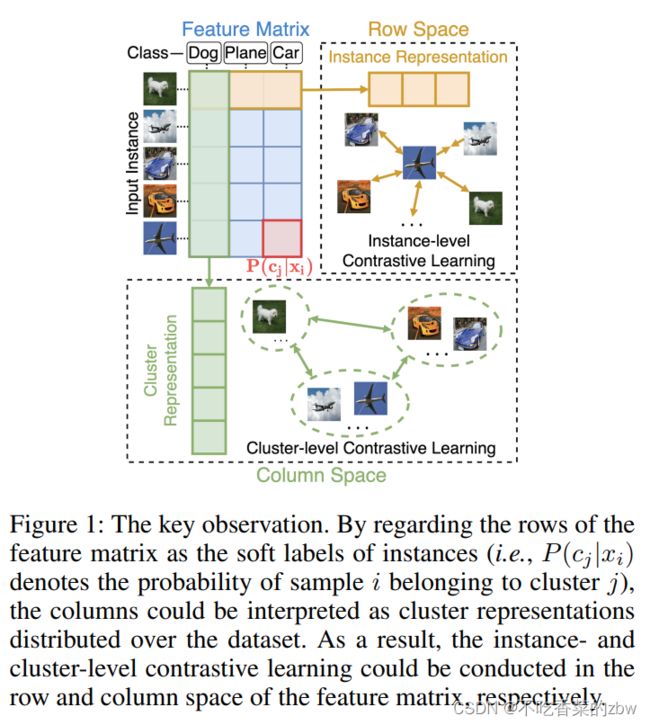
揭示了特征矩阵的行列与实例以及簇表达的关系

从实例级和簇级进行对比学习

端到端式的训练

---

相关工作

对比学习

深度聚类

---

论文方法

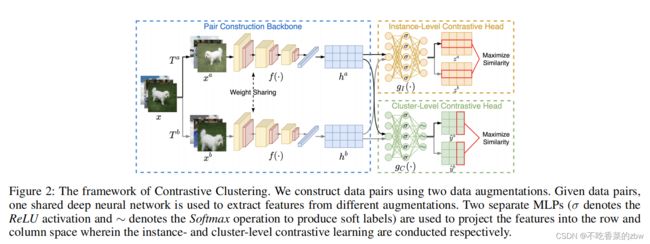
 模型主要由三部分构成，一对主干网络，实例级对比头和簇级对比头。简单来说，成对的主干网络通过数据增广来构建数据对，然后从这些增广的样本中提取特征，最后实例级对比头和簇级对比头分别从特征矩阵的行和列进行对比学习。训练过后，根据簇对比头预测的软标签得到簇的分布。

成对的主干网络

用数据增广来构建样本对。一个数据实例，随机从增广家族中生成两个数据增广，对数据使用增广得到两个增广的视图，即。合理的选择数据增广可以使得下游任务有更好的性能。本文用了五种数据增广，包含：Resized-Crop, ColorJitter, Grayscale, HorizontalFlip, and Gaussian-Blur。

用一个权重共享的神经网络来提取增广视图的特征，即

实例级对比头

对比学习的目标是增广正样本对的相似性，同时减小负样本对的相似性。在不同的情况下定义不同的样本对。本文中，将同一个实例生成的增广样本构成正样本对，负样本对则反之。

给定一个大小为的mini-batch，CC执行两种数据增广得到个数据即。对于具体的样本，总共有个样本对，其中只有其对应的样本构成的样本对为正样本对，其余的个样本对是负样本对。

为了减少对比损失导致的信息丢失，本文并不直接对特征矩阵进行对比学习。而是使用一个MLP记为将特征矩阵映射到子空间中，即，在此基础上应用实例级对比损失。用余弦距离衡量每个样本对的相似性，即：

 其中以及。对于一个给定的样本，其损失为：

 其中是温度参数。我们希望去区别数据集中所有的正样本，所以对每一个增广的视图计算实例级对比损失，即：

簇级对比头

跟着“标签也是一种特征”的思想，当将一个数据点映射到一个空间，该空间的维度等于簇的个数，此时，特征的第个元素可以视为分配给第个簇的概率，最后特征向量也相应的成为一个软标签。

让作为聚类头对一个mini-batch的第一个增广视图的输出（则为第二个增广），然后则可以解释为样本分配给簇的概率，其中是batch-size，是簇的个数。因为每一个样本只属于一个簇，所以的每一行都应该是one-hot的。至此，的第列可以视为第个簇的特征表示，每一列之间都应该相异。

与相似，也使用一个两层的MLP记为，将特征矩阵映射到维空间，即，其中，表示样本（的第i行）的软标签。为的第列，簇在第一个数据增广下的特征，将其与（簇的第二个增广特征）结合构建正的簇样本对，剩余的对都是负样本对。相似的，用余弦距离度量样本对之间的相似性，即：

 其中以及。不失一般性，用以下损失函数，来将簇与除之外的所有的簇进行区分，即：

 其中是簇级的温度参数。对所有簇进行遍历，簇级对比损失计算为：

 其中是一个mini-batch中的簇分配概率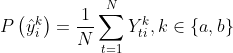的熵函数，这一项可以避免琐碎解（即，将所有的样本都分配到同一个簇中）

目标函数

---

消融实验设计

数据增广的重要性

对比头的效果

---

一句话总结

在SimCLR的框架下引入簇的矩阵解释，并应用于对比学习

---

论文好句摘抄（个人向）

(1)In this sense, the i-th column of Y a can be seen as a representation of the i-th cluster and all columns should differ from each other.