消息传递神经网络（MPNN）内容及代码实践

一、引言

为节点生成节点表征（Node Representation）是图计算任务成功的关键，我们要利用神经网络来学习节点表征。消息传递范式是一种聚合邻接节点信息来更新中心节点信息的范式，它将卷积算子推广到不规则数据领域，实现了图与神经网络的连接。消息传递范式因为简单、强大的特性，于是被人们广泛的使用。遵循消息传递范式的图神经网络被称为消息传递图神经网络。本节中，

• 首先我们将学习图神经网络生成节点表征的范式—消息传递（Message Passing）范式。
• 接着我们将初步分析PyG中的MessagePassing基类，通过继承此基类我们可以方便的构造一个图神经网络。
• 然后我们以继承MessagePassing基类的GCNConv类为例，学习如何通过继承MessagePassing基类来构造图神经网络。
• 再接着我们将对MessagePassing基类进行剖析。
• 最后我们将学习在继承MessagePassing基类的子类中覆写message(),aggreate(),message_and_aggreate()和update()，这些方法的规范。

二、消息传递范式介绍

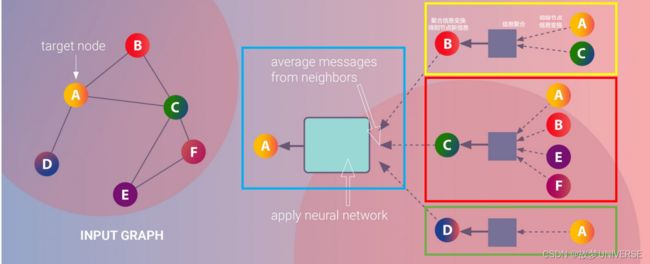
下面图片展示了基于消息传递范式的聚合邻接节点信息来更新中心节点信息的过程：
1、图中黄色方框部分展示的是一次邻接节点信息传递到中心节点的过程：B节点的邻接节点（A,C）的信息经过变换后聚合到B节点，接着B节点信息与邻接节点聚合信息一起经过变换得到B节点的新的节点信息。同时，分别如红色和绿色方框部分所示，遵循同样的过程，C,D节点的信息也被更新。实际上，同样的过程在所有节点上都进行了一遍，所有的节点的信息都更新了一遍。
2、这样的“邻接节点信息传递到中心节点的过程”会进行多次。如图中蓝色方框部分所示，A节点的邻接节点（B,C,D）的已经发生过一次更新的节点信息，经过变换、聚合、再变换产生了A节点第二次更新的节点信息。多次更新后的节点信息就作为节点表征。

消息传递图神经网络遵循上述的“聚合邻接节点信息的过程”，来生成节点表征。${x_i}^{(}k-1)$表示（k-1）层中节点$i$的节点表征，$e_{j,i}$表示从节点$j$到节点$i$的边的书信，消息传递图神经网络可以描述为
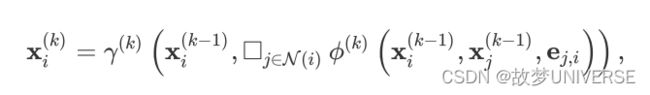其中方框表示可微分的、具有排列不变性（函数输出结果与输入参数的排列无关）的函数。具有排列不变性的函数有，sum()函数、mean()函数和max()函数。
$\gamma$和$\varphi$表示可微分的函数，如MLPs（多层感知器）
注（1）：神经网络的生成节点表征的操作称为节点嵌入（Node Embedding）,节点表征也可以称为节点嵌入。
注（2）：未经过训练的图神经网络生成的节点表征还不是好的表征，好的表征可用于衡量节点之间的相似性。通过监督学习对图神经网络做很好的训练，图神经网络才可以生成好的节点表征。
注（3）：节点表征与节点属性的区分：遵循被广泛使用的约定，节点属性data.x是节点第0层节点表征，第h层的节点表征经过一次的节点间消息传递产生第h+1层的节点表征。不过，节点属性不单指data.x，广义上它就指节点的属性，如节点的度等。

三、MessagePassing基类初步分析

Pytorch Geometric(PyG)提供了MessagePassing基类，它封装了“消息传递”的运行流程。通过继承MessagePassing基类，可以方便的构造消息传递神经网络。构造一个最简单的消息传递图神经网络类，我们只需定义message()方法（$\varphi$）、update()方法（$\gamma$），以及使用的消息聚合方案（aggr=“add”、aggr="mean"或aggr=“max”）。这一切是在以下方法的帮助下完成的：

• MessagePassing(aggr=“add”,flow=“source_to_target”,node_dim=-2)(对象初始化方法)：

  • aggr:定义要使用的聚合方案（“add”,"mean"或“max”）
  • flow:定义消息传递的流向（“source_to_target”或"target_to_source"）
  • node_dim:定义沿着哪个维度传播，默认值为-2，也就是节点表征张量（Tensor）的哪一个维度是节点维度。节点表征张量x形状为[num_nodes,num_features],其第0维度（也就是第-2维度）是节点维度，其第一维度（也是第-1维度）是节点表征维度，所以我们可以设置node_dim=2.
  • 注：MessagePassing(…)等同于MessagePassing._init_(…)

• MessagePassing.propagate(edge_index,size=None,**kwargs):

  • 开始传递消息的起始调用，在此方法中message、update等方法被调用。
  • 它以edge_index(边的端点的索引)和flow(消息的流向)以及额外的一些数据为参数。
  • 注意，propagate（）不局限于基于形状为[N,N]的对称邻接矩阵进行“消息传递过程”。基于非对称的邻接矩阵进行消息传递，需要size=(N,M)。
  • 如果设置size=None，则认为邻接矩阵是对称的。

• MessagePassing.message(…):

  • 首先要确定要给节点$i$传递消息的边的集合：

    • 如果flow=“source_to_target”,则是（$j$,$i$)$\in$$E$的边的集合；
    • 如果flow=“target_to_source”,则是（$i$,$j$)$\in$$E$的边的集合。

  • 接着为各条边创建要传递给节点$i$的消息，即实现$\varphi$函数。

• MessagePassing.message(…)方法可以接收传递给MessagePassing.propagate(edge_index,size=None,**kwargs)方法的所有参数，我们在message()方法的参数列表里定义要接收的参数，例如我们要接收x,y,z参数，则我们应该定义message(x,y,z)方法。

• 传递给propagate（）方法的参数，如果是节点的属性的话，可以被拆分成属于中心节点的部分和属于邻接节点的部分，只需在变量名后面加上_i或_j。例如我们自己定义的message方法包含参数x_i，那么首先propagate()方法将节点表征拆分成中心节点表征和邻接节点表征，接着propagate()方法调用message（）方法并传递中心节点表征给参数x_i。而如果我们自己定义的message()方法包含参数x_j,那么propagate（）方法会传递邻接节点表征给参数x_j.

• 我们用$i$表示“消息传递”中的中心节点，用$j$表示“消息传递”中的邻接节点。

• MessagePassing.aggregate(…):

  • 将从源节点传递过来的消息聚合在目标节点上，一般可选的聚合方式有sum,mean和max。

• MessagePassing.message_and_aggregate(…):

  • 在一些场景里，邻接节点信息变换和邻接节点消息聚合这两项操作可以融合在一起，那么我们可以在此方法里定义这两项操作，从而让程序更加高效。

• MessagePassing.update(aggr_out,…)

  • 为每个节点$i$$\in$$V$更新节点表征，即实现$\gamma$函数。此方法以aggregate方法的输出为第一个参数，并接收所有传递给propagate()方法的参数。

四、MessagePassing子类实例

我们以继承MessagePassing基类的GCNConv类为例，学习如何通过继承MessagePassing基类来实现一个简单的图神经网络。
GCNConv的数学定义为

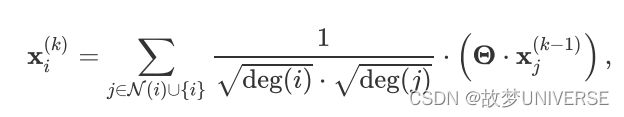
其中，邻接节点的表征${x_j}^{(k-1)}$首先通过与权重矩阵$\Theta$相乘进行变换，然后按端点的度deg($i$),deg($j$)进行归一化处理，最后进行求和。这个公式可以分为以下几个步骤：

1. 向邻接矩阵添加自环
2. 对节点表征做线性变换
3. 计算归一化系数
4. 归一化邻接节点的表征
5. 将相邻节点表征聚合
   步骤1-3通常在消息传递发生之前计算的。步骤4-5可以使用MessagePassing基类轻松处理。该层的全部实现如下所示。

import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops,degree

class GCNConv(MessagePassing):
    def _init__(self,in_channels,out_channels):
        super(GCNConv,self).__init__(aggr = 'add',flow = 'source_to_target')

        #"add" aggeration (step 5)
        #flow = 'source_to_target'表示消息从源节点传播到目标节点

        self.lin = torch.nn.Linear(in_channels,out_channels)

    def forward(self,x,edge_index):

        #x has shape [N,in_channels]
        #edge_index has shape [2,E]
        #step 1:Add self_loops to the adjacency matrix

        edge_index,_ = add_self_loops(edge_index,num_nodes = x.size(0))

        #step2:Linearly transform node feature matrix

        x = self.lin(x)

        #step3:compute normalization

        row,col = edge_index
        deg = degree(col,x.size(0),dtype = x.dtype)
        deg_inv_sqrt = deg.pow(-0.5)
        norm = deg_inv_sqrt[row]*deg_inv_sqrt[col]

        #step4-5:start propagating messages.

        return self.propagate(edge_index,x = x,norm = norm)
    
    def message(self,x_j,norm):
        
        #x_j has shape [E,out_channels]
        #step4:Normalize node features

        return norm.view(-1,1)*x_j

GCNConv继承了MessagePassing并以“求和”作为邻域节点信息聚合方式。该层的所有逻辑都发生在其forward()方法中。在这里，我们首先使用torch_geometric.utils.add_self_loops()函数向我们的边索引添加自环（step1），以及通过调用torch.nn.Linear实例对节点表征进行线性变换（step2）.propagate()方法也在forward方法中被调用，propagate（）方法被调用后节点间的信息传递开始执行。

归一化系数是由每个节点的节点度得出的，它被转换为每天边的节点度。结果被保存在形状为[num_edges,]的变量norm中（step3）

在message（）方法中，我们需要通过norm对邻接节点表征x_j进行归一化处理。

通过以上内容的学习，我们便掌握了创建一个仅包含一次“消息传递过程”的图神经网络的方法。如下代码所示，我们可以很方便的初始化和调用它：

from torch_geometric.datasets import Planetoid

dataset = Planetoid(root = 'dataset',name = 'Cora')
data = dataset[0]

net = GCNConv(data.num_features,64)
h_nodes = net(data.x,data.edge_index)
print(h_nodes.shape)

通过串联多个这样的简单图神经网络，我们就可以构建复杂的图神经网络模型。

五、MessagePassing基类剖析

在__init__()方法中，我们可以看到程序会检查子类是否实现了message_and_aggregate()方法，并将检查结果赋值给fuse属性。

class MessagePassing(torch.nn.Module):
    r"""Base class for creating message passing layers of the form

    .. math::
        \mathbf{x}_i^{\prime} = \gamma_{\mathbf{\Theta}} \left( \mathbf{x}_i,
        \square_{j \in \mathcal{N}(i)} \, \phi_{\mathbf{\Theta}}
        \left(\mathbf{x}_i, \mathbf{x}_j,\mathbf{e}_{j,i}\right) \right),

    where :math:`\square` denotes a differentiable, permutation invariant
    function, *e.g.*, sum, mean, min, max or mul, and
    :math:`\gamma_{\mathbf{\Theta}}` and :math:`\phi_{\mathbf{\Theta}}` denote
    differentiable functions such as MLPs.
    See `here `__ for the accompanying tutorial.

    Args:
        aggr (string, optional): The aggregation scheme to use
            (:obj:`"add"`, :obj:`"mean"`, :obj:`"min"`, :obj:`"max"`,
            :obj:`"mul"` or :obj:`None`). (default: :obj:`"add"`)
        flow (string, optional): The flow direction of message passing
            (:obj:`"source_to_target"` or :obj:`"target_to_source"`).
            (default: :obj:`"source_to_target"`)
        node_dim (int, optional): The axis along which to propagate.
            (default: :obj:`-2`)
        decomposed_layers (int, optional): The number of feature decomposition
            layers, as introduced in the `"Optimizing Memory Efficiency of
            Graph Neural Networks on Edge Computing Platforms"
            `_ paper.
            Feature decomposition reduces the peak memory usage by slicing
            the feature dimensions into separated feature decomposition layers
            during GNN aggregation.
            This method can accelerate GNN execution on CPU-based platforms
            (*e.g.*, 2-3x speedup on the
            :class:`~torch_geometric.datasets.Reddit` dataset) for common GNN
            models such as :class:`~torch_geometric.nn.models.GCN`,
            :class:`~torch_geometric.nn.models.GraphSAGE`,
            :class:`~torch_geometric.nn.models.GIN`, etc.
            However, this method is not applicable to all GNN operators
            available, in particular for operators in which message computation
            can not easily be decomposed, *e.g.* in attention-based GNNs.
            The selection of the optimal value of :obj:`decomposed_layers`
            depends both on the specific graph dataset and available hardware
            resources.
            A value of :obj:`2` is suitable in most cases.
            Although the peak memory usage is directly associated with the
            granularity of feature decomposition, the same is not necessarily
            true for execution speedups. (default: :obj:`1`)
    """

    special_args: Set[str] = {
        'edge_index', 'adj_t', 'edge_index_i', 'edge_index_j', 'size',
        'size_i', 'size_j', 'ptr', 'index', 'dim_size'
    }

    def __init__(self, aggr: Optional[str] = "add",
                 flow: str = "source_to_target", node_dim: int = -2,
                 decomposed_layers: int = 1):

        super().__init__()

        self.aggr = aggr
        assert self.aggr in ['add', 'sum', 'mean', 'min', 'max', 'mul', None]

        self.flow = flow
        assert self.flow in ['source_to_target', 'target_to_source']

        self.node_dim = node_dim
        self.decomposed_layers = decomposed_layers

        self.inspector = Inspector(self)
        self.inspector.inspect(self.message)
        self.inspector.inspect(self.aggregate, pop_first=True)
        self.inspector.inspect(self.message_and_aggregate, pop_first=True)
        self.inspector.inspect(self.update, pop_first=True)
        self.inspector.inspect(self.edge_update)

        self.__user_args__ = self.inspector.keys(
            ['message', 'aggregate', 'update']).difference(self.special_args)
        self.__fused_user_args__ = self.inspector.keys(
            ['message_and_aggregate', 'update']).difference(self.special_args)
        self.__edge_user_args__ = self.inspector.keys(
            ['edge_update']).difference(self.special_args)

        # Support for "fused" message passing.
        self.fuse = self.inspector.implements('message_and_aggregate')

“消息传递过程”是从propagate方法被调用开始执行的

def propagate(self, edge_index: Adj, size: Size = None, **kwargs):
        r"""The initial call to start propagating messages.

        Args:
            edge_index (Tensor or SparseTensor): A :obj:`torch.LongTensor` or a
                :obj:`torch_sparse.SparseTensor` that defines the underlying
                graph connectivity/message passing flow.
                :obj:`edge_index` holds the indices of a general (sparse)
                assignment matrix of shape :obj:`[N, M]`.
                If :obj:`edge_index` is of type :obj:`torch.LongTensor`, its
                shape must be defined as :obj:`[2, num_messages]`, where
                messages from nodes in :obj:`edge_index[0]` are sent to
                nodes in :obj:`edge_index[1]`
                (in case :obj:`flow="source_to_target"`).
                If :obj:`edge_index` is of type
                :obj:`torch_sparse.SparseTensor`, its sparse indices
                :obj:`(row, col)` should relate to :obj:`row = edge_index[1]`
                and :obj:`col = edge_index[0]`.
                The major difference between both formats is that we need to
                input the *transposed* sparse adjacency matrix into
                :func:`propagate`.
            size (tuple, optional): The size :obj:`(N, M)` of the assignment
                matrix in case :obj:`edge_index` is a :obj:`LongTensor`.
                If set to :obj:`None`, the size will be automatically inferred
                and assumed to be quadratic.
                This argument is ignored in case :obj:`edge_index` is a
                :obj:`torch_sparse.SparseTensor`. (default: :obj:`None`)
            **kwargs: Any additional data which is needed to construct and
                aggregate messages, and to update node embeddings.
        """
        decomposed_layers = 1 if self._explain else self.decomposed_layers

        for hook in self._propagate_forward_pre_hooks.values():
            res = hook(self, (edge_index, size, kwargs))
            if res is not None:
                edge_index, size, kwargs = res

        size = self.__check_input__(edge_index, size)

        # Run "fused" message and aggregation (if applicable).
        if (isinstance(edge_index, SparseTensor) and self.fuse
                and not self._explain):
            coll_dict = self.__collect__(self.__fused_user_args__, edge_index,
                                         size, kwargs)

            msg_aggr_kwargs = self.inspector.distribute(
                'message_and_aggregate', coll_dict)
            for hook in self._message_and_aggregate_forward_pre_hooks.values():
                res = hook(self, (edge_index, msg_aggr_kwargs))
                if res is not None:
                    edge_index, msg_aggr_kwargs = res
            out = self.message_and_aggregate(edge_index, **msg_aggr_kwargs)
            for hook in self._message_and_aggregate_forward_hooks.values():
                res = hook(self, (edge_index, msg_aggr_kwargs), out)
                if res is not None:
                    out = res

            update_kwargs = self.inspector.distribute('update', coll_dict)
            out = self.update(out, **update_kwargs)

        # Otherwise, run both functions in separation.
        elif isinstance(edge_index, Tensor) or not self.fuse:
            if decomposed_layers > 1:
                user_args = self.__user_args__
                decomp_args = {a[:-2] for a in user_args if a[-2:] == '_j'}
                decomp_kwargs = {
                    a: kwargs[a].chunk(decomposed_layers, -1)
                    for a in decomp_args
                }
                decomp_out = []

            for i in range(decomposed_layers):
                if decomposed_layers > 1:
                    for arg in decomp_args:
                        kwargs[arg] = decomp_kwargs[arg][i]

                coll_dict = self.__collect__(self.__user_args__, edge_index,
                                             size, kwargs)

                msg_kwargs = self.inspector.distribute('message', coll_dict)
                for hook in self._message_forward_pre_hooks.values():
                    res = hook(self, (msg_kwargs, ))
                    if res is not None:
                        msg_kwargs = res[0] if isinstance(res, tuple) else res
                out = self.message(**msg_kwargs)
                for hook in self._message_forward_hooks.values():
                    res = hook(self, (msg_kwargs, ), out)
                    if res is not None:
                        out = res

                # For `GNNExplainer`, we require a separate message and
                # aggregate procedure since this allows us to inject the
                # `edge_mask` into the message passing computation scheme.
                if self._explain:
                    edge_mask = self._edge_mask
                    if self._apply_sigmoid:
                        edge_mask = edge_mask.sigmoid()
                    # Some ops add self-loops to `edge_index`. We need to do
                    # the same for `edge_mask` (but do not train those).
                    if out.size(self.node_dim) != edge_mask.size(0):
                        edge_mask = edge_mask[self._loop_mask]
                        loop = edge_mask.new_ones(size[0])
                        edge_mask = torch.cat([edge_mask, loop], dim=0)
                    assert out.size(self.node_dim) == edge_mask.size(0)
                    out = out * edge_mask.view([-1] + [1] * (out.dim() - 1))

                aggr_kwargs = self.inspector.distribute('aggregate', coll_dict)
                for hook in self._aggregate_forward_pre_hooks.values():
                    res = hook(self, (aggr_kwargs, ))
                    if res is not None:
                        aggr_kwargs = res[0] if isinstance(res, tuple) else res
                out = self.aggregate(out, **aggr_kwargs)
                for hook in self._aggregate_forward_hooks.values():
                    res = hook(self, (aggr_kwargs, ), out)
                    if res is not None:
                        out = res

                update_kwargs = self.inspector.distribute('update', coll_dict)
                out = self.update(out, **update_kwargs)

                if decomposed_layers > 1:
                    decomp_out.append(out)

            if decomposed_layers > 1:
                out = torch.cat(decomp_out, dim=-1)

        for hook in self._propagate_forward_hooks.values():
            res = hook(self, (edge_index, size, kwargs), out)
            if res is not None:
                out = res

        return out

参数简介：

• edge_index: 边端点索引，它可以是Tensor类型或SparseTensor类型。

  • 当flow="source_to_target"时，节点edge_index[0]的信息将被传递到节点edge_index[1]，
  • 当flow="target_to_source"时，节点edge_index[1]的信息将被传递到节点edge_index[0]

• size: 邻接节点的数量与中心节点的数量。

  • 对于普通图，邻接节点的数量与中心节点的数量都是N，我们可以不给size传参数，即让size取值为默认值None。
  • 对于二部图，邻接节点的数量与中心节点的数量分别记为M, N，于是我们需要给size参数传一个元组(M, N)。

• kwargs: 图其他属性或额外的数据。

• propagate()方法首先检查edge_index是否为SparseTensor类型以及是否子类实现了message_and_aggregate()方法，如是就执行子类message_and_aggregate方法；否则依次执行子类的message(),aggregate(),update()三个方法。

七、总结

消息传递范式是一种聚合邻接节点信息来更新中心节点信息的范式，它将卷积算子推广到了不规则数据领域，实现了图与神经网络的连接。该范式包含这样三个步骤：（1）邻接节点信息变换（2）邻接节点信息聚合到中心节点（3）聚合信息变换。由于简单且强大的特性，消息传递范式被广泛采用。基于此范式，我们可以定义聚合邻接节点信息来生成中心节点表征的图神经网络。在PyG中，MessagePassing基类是所有基于消息传递范式的图神经网络的基类，它大大的方便了对图神经网络的构建。