AI —— Bayes Rule

重点一、Bayes’ Rule 贝叶斯法则
P(a | b) P(b) = P(a, b) = P(b | a) P(a)
P(a | b) = P(b | a) P(a)/P(b)

基础概率论知识：
全概率公式==》由条件推结论

贝叶斯公式==》由结论去判断条件

重点二、条件独立
绝对独立：

P(x,y) = P(x)P(y)
P(x|y) = P(x)  or  P(y|x) = P(y)

由联合概率公式的链式法则，可以简化条件独立下的链式法则：

P(G, C1,1 , … C3,3) = P(G) P(C1,1 | G) P(C1,2 | G) P(C1,3 | G) …
P(C3,3 | G)

条件独立性是我们关于不确定环境的最基本和最强大的知识形式。
Conditional independence is our most basic and robust form of knowledge about uncertain environments.

X is conditionally independent of Y given Z if and only if:
（在给定Z的条件下，X与Y是独立的当且仅当:）
∀ x,y,z
P(x | y, z) = P(x | z)
or, equivalently, if and only if
∀x,y,z
P(x, y | z) = P(x | z) P(y | z)

【注意】：
| 进行分割，前后均为整体，，存在部分为一个整体

重点三、贝叶斯网络 Bayes nets
Bayes nets: a technique for describing complex joint distributions (models) using simple, conditional distributions
贝叶斯网:一种用简单的条件分布描述复杂联合分布(模型)的技术

Bayes net = Topology (graph) + Local Conditional Probabilities
贝叶斯网=拓扑(图)+局部条件概率

Use local causality/conditional independence
使用局部因果关系/条件独立
Example of Bayes’ Net——Car Insurance:

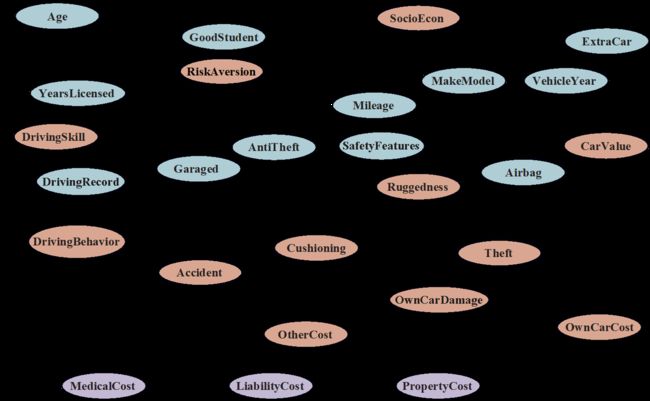
题型：利用贝叶斯网络计算条件概率
公式一：P(X1,…,Xn) = ∏i P(Xi | Parents(Xi))
关于其父节点的条件概率作累乘
精髓：从原始的条件概率的链式法则转化而来，结合条件独立的前提，利用贝叶斯网络进行求解，贝叶斯网=拓扑(图)+局部条件概率
EXAMPLE:
题目中的条件概率分布表是已知的。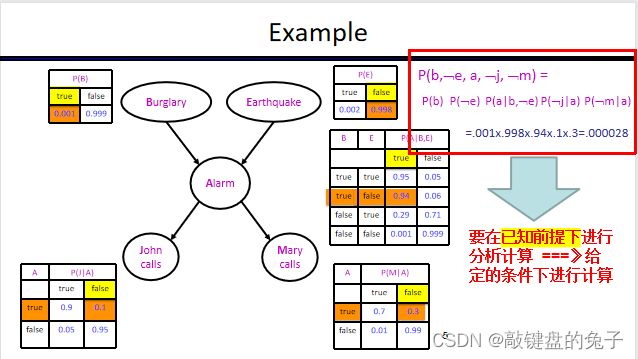
【注意】：
A：大写的字母表示随机变量，即事件；
B：小写的字母表示实数，即事件发生的取值

重点四：利用贝叶斯网络进行精准推理
Bayes Nets: Exact Inference
Inference by Enumeration in Bayes Net
贝叶斯网络中的枚举推理
公式二: P(Q | e) =ɑ ∑h P(Q , h, e)
【举例】:

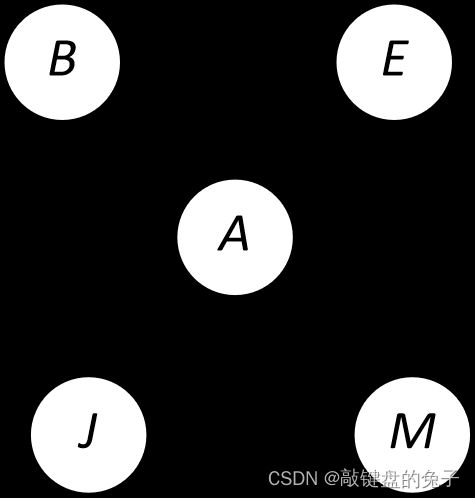
P(B | j, m) = α ∑e,a P(B, e, a, j, m)
= α ∑e,a P(B) P(e)P(a|B,e)P(j|a) P(m|a)

精髓：根据已知的条件，将其他的所有变量全部补齐，然后作条件概率的累加
注意虽然这里的变量是小写（公式里全部自己补的都是小写），但还是所有的情况都要考虑，相当于大写字母，表示事件，所有的情况都要考虑到，真假都要计算，然后进行累加，然后利用上述公式一进行计算

题型：利用贝叶斯推理，计算条件概率
分两步走：先乘法+再累加
题：Query P(B | j,m)
解：① Choose A
把所有含A 的条件全部选择出来，前面的依旧在前面，后面的依旧在后面。

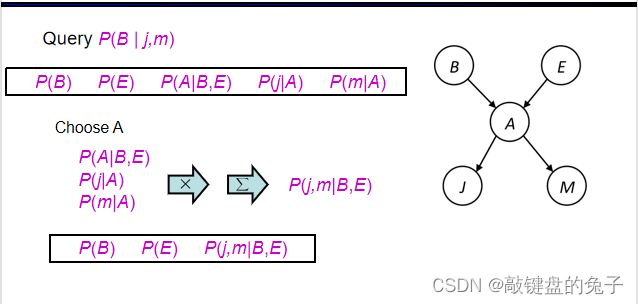
②choose E
（同理)

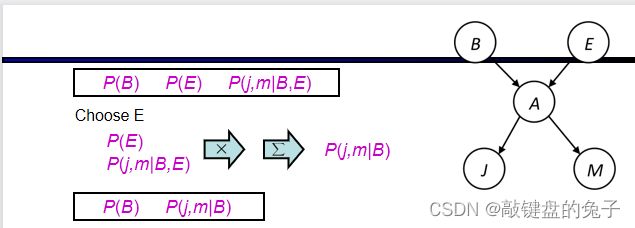
③ finish with B 并进行normalize
(同理）

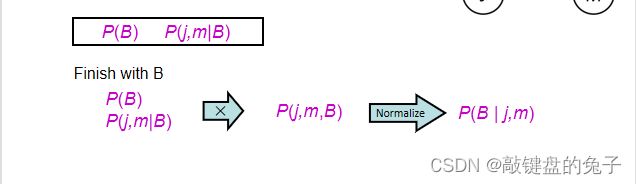
整个操作都是根据公式二进行的，变量的选取顺序没有关系。