人工智能:搜索策略
一、无信息的搜索策略
1.宽度优先搜索
2.一致代价搜索
当每一步的行动代价都相等时宽度优先搜索是最优的,因为它总是先扩展深度最浅的未扩展结点。
一致代价搜索( uniform-cost search)扩展的是路径消耗(gn)最小的结点n。这可以通过将边缘结点集组织成按g值排序的队列来实现。算法如图3.14所示

3.深度优先搜索
4. 深度受限搜索
5. 迭代加深的深度优先搜索
5.双向搜索
双向搜索( bidirectional search)的思想是同时运行两个搜索个从初始状态向前搜索同时另一个从目标状态向后搜索—希望它们在中间某点相遇,此时搜索终止(图3.20)。理由是 b d 2 + b d 2 b^{\frac{d}{2}}+b^{\frac{d}{2}} b2d+b2d要比 b d b^d bd小很多,或者可以看图,两个小圆的面积相加比以起点为中心到达
无信息搜索策略对比

一致代价搜索由路径代价而不是深度来引导,所以算法复杂度不能简单地用b和d来表示。引入 C ∗ C^* C∗标识最优解的代价,假设每个行动的代价至少为 ϵ \epsilon ϵ。
那么最坏情况下,算法的时间和空间复杂度为 O ( b 1 + [ C ∗ / ϵ ] ) O(b^{1+[C^*/\epsilon]}) O(b1+[C∗/ϵ]),要比b大得多。这是因为一致代价搜索在探索包含代大的行动之前,经常会先探索代价小的行动步骤所在的很大的搜索树。当所有的单步耗散都相等的时候, O ( b 1 + [ C ∗ / ϵ ] ) O(b^{1+[C^*/\epsilon]}) O(b1+[C∗/ϵ])就是 b d + 1 b^{d+1} bd+1。此时,一致代价搜索与宽度优先搜索类似,除了算法终止条件,宽度优先搜索在找到解时终止,而一致代价搜索则会检査目标深度的所有结点看谁的代价最小;这样,在这种情况下一致代价搜索在深度d无意义地做了更多的工作。
二、有信息的搜索策略
1. 最佳优先搜索
最佳优先搜索(best- first search)是一般TREE-SEARCH和 GRAPH- SEARCH算法的一个实例,结点是基于评估函数f(n)值被选择扩展的。评估函数被看作是代价估计,因此评估值最低的结点被选择首先进行扩展。最佳优先图搜索的实现与一致代价搜索类似,不过最佳优先是根据f值而不是g值对优先级队列排队. 以下的贪婪最佳优先搜索和A*搜索时最佳优先搜索的两个特例(具体实现)。
2. 贪婪最佳优先搜索
该算法(greedy best-first search)试图拓展距离目标最近的结点。即评估函数 f(n) = h(n) (heuristic) = estimate of cost from n to goal
完备性:不完备的(也就是说不一定能找到问题的解)
算法复杂度:
(1)时间复杂度: O ( b m ) O(b^m) O(bm)
(2)空间复杂度: O ( b m ) O(b^m) O(bm)
其中,b是邻居节点的最大数量,m是搜索空间的最大深度。
缺点:不完备的,可能会卡在循环中,例如,我们考虑从lasi到Fagaras的问题,从直线距离上讲,lasi的邻居中Neamt距离Fagaras最近,因此会走到Neamt,而Neamt只有一个邻居,因此会重新回到Iasi,因此会陷入死循环 I a s i → N e a m t → I a s i → N e a m t Iasi\rightarrow Neamt\rightarrow Iasi\rightarrow Neamt Iasi→Neamt→Iasi→Neamt。

3. A*搜索
(1)A*搜索的算法流程
该算法流程与一致代价搜索类似(如下所示),除了A*使用的代价函数是g+h而不是g
//优先队列为小根堆
WHILE 优先队列不为空
取出队头并扩展
将扩展节点以估价值+当前值为优先级入队
END WHILE
补充:一致代价搜索的过程:

而一致代价搜索它的算法流程又跟优先队列搜索相关。在图3.15的搜索中都起到了作用,图中的搜索是从 Sibiu到 Bucharest。 Sibiu的后继包括 Rimnicu Vilcea和 Fagaras,代价分别为80和99。最小代价结点为 Rimnicu Vilcea被选择扩展,此时加入了 Pitesti代价为80+97=177。所以这时的最小代价结点为 Fagaras,扩展它得到 Bucharest代价为99+211=310。目标结点已经生成,但是一致代价搜索算法还在继续,选择 Pitesti扩展得到到达 Bucharest的第二条路代价为80+97+101=278。现在算法则需要检查新路径是不是要比老路径好;确实是新的好,于是老路径被丢弃。 Bucharest, g代价为278,被选择扩展算法返回。
启发式函数是:
f(n) = g(n) +h(n)
g(n)是从开始结点到节点n的路径代价,而h(n)是从节点n到目标结点的最小代价路径的估计值。
(2)保证最优性的条件
i. 可采纳性(Admissibility)
一个可采纳的启发式是指这个启发式从不会过高估计到达目标的代价,也就是f(n)永远不会超过经过节点n的解的实际代价。
定理1: 如果h(n)是可采纳的,那么A*的树搜索版本是最优的
举例说明: 需补充
ii. 一致性(Consistency)
如果对于每个节点n和通过任一行动a生成的n的每一个后继节点n’,从节点到达目标的估计代价不大于从n到n’的单步代价与从n’到达目标的估计代价之和:
h ( n ) ≤ c ( n , a , n ′ ) + h ( n ‘ ) h(n) \leq c(n,a,n') + h(n‘) h(n)≤c(n,a,n′)+h(n‘)
一致性规定了启发性函数的特点(也就是让我们在设计启发性函数的时候满足以上不等式)
可以看到,在一致代价搜索中,h(n)即为距离目标的直线距离,可以看到,如果所有节点到目标的直线距离满足上述一致性公式,则图1所示的无法找到解的状况将不复存在。该性质确保了在搜索的过程中不存在往回走的情况,因此,我们可得到第二个定理。
定理2: 如果h(n)是一致的,那么A*的图搜索版本是最优的,即一定能找到最优解
(3)算法分析
i. 算法复杂度:
复杂度结构十分依赖于状态空间的定义。对于只有一个目标状态的状态空间,A*的时间复杂度是指数级的。
对于那些每步骤为常量的问题,时间复杂度的增长是最优解所在深度d的函数,这可以通过启发式的决定错误和相对错误来分析。绝对误差定义为 △ = h ∗ − h \triangle=h^*-h △=h∗−h,其中 h ∗ h^* h∗是从根节点到目标节点的实际代价,相对误差定义为 ϵ = ( h ∗ − h ) / h ∗ \epsilon = (h^*-h)/h^* ϵ=(h∗−h)/h∗. h是对代价的估计,h比 h ∗ h^* h∗越小,那么在找最优解的过程中误判(错走到不是实际代价最小的路径)的几率就越大。
对于简单状态空间的问题,A*的时间复杂度可以用 O ( b △ ) O(b^{\triangle}) O(b△)标识,考虑每步骤代价均为常量,我们可以把这记为 O ( b ϵ d ) O(b^{\epsilon d}) O(bϵd),其中d是解所在的深度。
(1)时间复杂度: O ( b ϵ d ) O(b^{\epsilon d}) O(bϵd)
(2)空间复杂度:Keeps all nodes in memory
ii. 优缺点:
优点:是完备的,而且能找到最优解
缺点:需要花费大量内存,常常在计算完之前就耗尽了它的所有内存。
4. 存储受限的启发式搜索
(1)IDA*算法
IDA算法,也就是迭代加深的A算法,可以在一定程度上减少对存储的浪费。
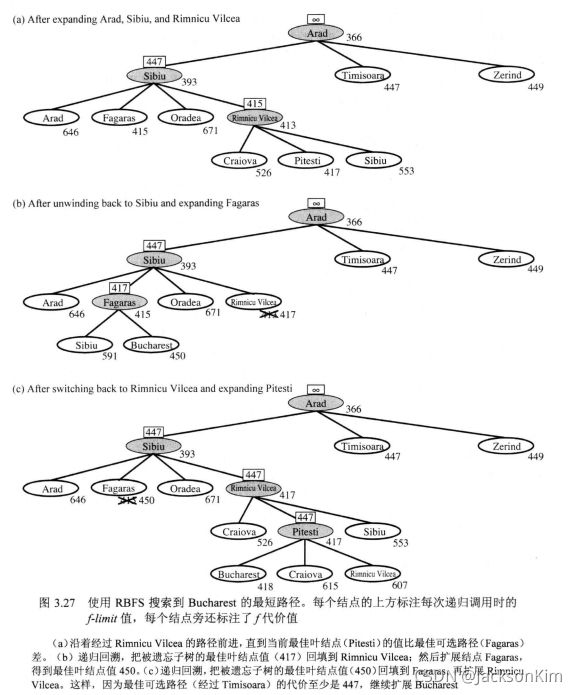
(2)递归最佳优先搜索(RBFS)
递归最佳优先搜素(RBFS)是一个简单的递归算法,它试图模仿标准的最佳优先搜索的操作,但只使用线性的存储空间。算法如图3.26所示。它的结构和递归深度优先搜索类似,但是它不会不确定地沿着当前路径继续,它用变量fimi跟踪记录从当前结点的祖先可得到的最佳可选路径的∫值。如果当前结点超过了这个限制,递归将回到可选路径上。

IDA和RBFS的问题在于它们使用的内存过于小了。在两次迭代之间,IDA只保留1个数字:当前的f代价界限值。RBFS在内存中保留的信息多一些,但也只用到线性空间即便有更多可用的内存,RBFS也没有办法利用。因为两个算法都忘记了它们做过什么所以算法终止时有些状态可能重复扩展多次。更坏的是,图中的冗余路径会带来复杂度的潜在的指数级的增长(见3.3节)。
(2)MA*
内存受限A*(MA*),简化的MA*(SMA*)
SMA算法很像A算法,扩展最佳叶结点直到内存耗尽。就是说,要在搜索树中加入新结点就得抛弃个旧结点。SMA总是丢弃最差的叶结点即f值最高的结点。像RBFS一样,SMA把被遗忘结点的值回填给父结点。这样,被遗忘子树的祖先结点可以了解子树的最佳路径。有了这个信息,当所有其他路径看来比被遗忘路径要差的时候,SMA*可以重新生成该子树。换句话说,如果结点n的所有子孙结点都被遗忘了,我们不知道从n该走哪条路,但是我们知道从n去别处是否值得。
三、局部搜索算法
局部搜索算法适用于那些关注解状态而不是路径代价的问题。
1. 爬山法
2. 模拟退火搜索
模拟退火算法的内层循环(图4.5)与爬山法类似。只是它没有选择最佳移动,选择的是随机移动。如果该移动使情况改善,该移动则被接受。否则,算法以某个小于1的概率接受该移动。如果移动导致状态“变坏”,概率则成指数级下降一一评估值△E变坏。这个概率也随“温度”7降低而下降:开始ア高的时候可能允许“坏的”移动,T越低则越不可能发生。如果调度让T下降得足够慢,算法找到全局最优解的概率逼近于1。