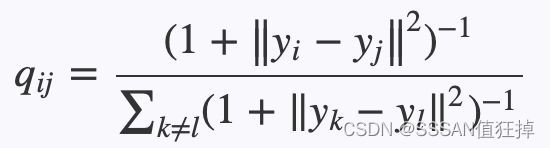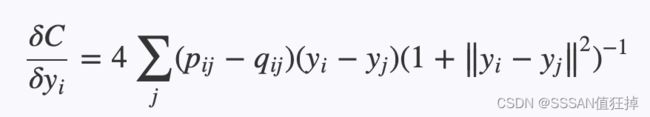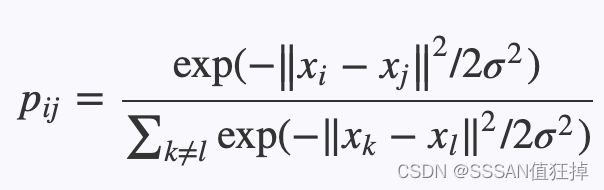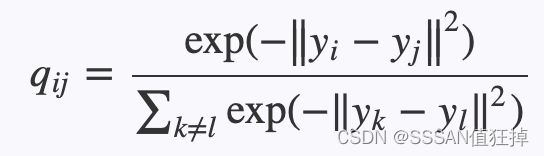- 森林的智慧:随机森林与集成学习的民主之道
田园Coder
人工智能科普人工智能科普
当约阿夫·弗罗因德和罗伯特·沙皮尔提出的AdaBoost算法在90年代末期以其强大的预测精度震惊机器学习界,展示了“团结弱者为强者”的集成魅力时,另一种集成思想也在悄然孕育。这种思想同样信奉“众人拾柴火焰高”,但走的是一条与AdaBoost截然不同的路径:它不执着于反复调整数据权重去“关注”被前序模型分错的困难样本,而是致力于创造尽可能多样化的模型,然后让这些模型平等地投票。它的核心哲学是:如果每
- 工具学习_CVE Binary Tool
1.工具概述CVEBinaryTool是一个免费的开源工具,可帮助您使用国家漏洞数据库(NVD)常见漏洞和暴露(CVE)列表中的数据以及Redhat、开源漏洞数据库(OSV)、Gitlab咨询数据库(GAD)和Curl中的已知漏洞数据来查找软件中的已知脆弱性。该工具有两种主要操作模式:二进制扫描程序:可帮助您确定哪些包可能已作为软件的一部分包含在内。该程序包括360检查器,扫描程序主要适用于常见的
- 无人机3控接力模式技术分析
云卓SKYDROID
无人机云卓科技遥控器通道高科技
一、运行方式1.接力控制流程位置触发切换:飞控中心实时监测无人机位置,当进入预设的切换路线(如靠近下一个机库或控制器覆盖范围)时,触发切换流程。控制权请求与验证:当前控制器(如控制器A)向目标控制器(控制器B)发送接管请求。控制器B分析无人机与自身的空间关系(如竖直夹角需在20°~30°范围内),满足条件则接收控制权,否则拒绝。密钥认证接管:目标控制器与无人机通过握手机制交换序列号,飞控中心下发加
- 智能停车场管理系统:如何实现停车场精细化运营管理?
捷码小编
数字孪生低代码信息可视化软件需求智慧城市
分享大纲:1、可视化运营中枢:全局掌握车场动态2、后台管理:灵活查看数据,配置规则策略3、移动化协同:提升现场管理效率在传统模式下,面对放下停车资源日益紧张的今天,停车场逐渐面临管理粗放、效率低下、车主体验差等问题。杭州远眺科技基于AI+低代码打造的智能停车场管理系统,为停车运营方提供一套全流程、多终端、可简单配置的数字化管理方案。可视化运营中枢:全局掌握车场动态智能停车场管理系统:如何实现停车场
- Python —— pandas 主要方法 和 常用属性(一)
墨码
笔记知识点python数据分析Pandas
Pandas基础类型Series类型创建SeriesSeries的自定义索引读取SeriesPandaspandas数据分析统计包,是一款功能强大的用于数据分析的操作工具,由于其的实用性对操作数据的方便性广受欢迎,今天就来学习一下Pandas数据包的用法吧!在此之前推荐了解一下numpy基础类型说道数据类型,大家熟知的大概都是intstrbool等数据类型,或者是Python中的listtuple
- 机器学习:集成学习方法之随机森林(Random Forest)
慕婉0307
机器学习集成学习机器学习随机森林
一、集成学习与随机森林概述1.1什么是集成学习集成学习(EnsembleLearning)是机器学习中一种强大的范式,它通过构建并结合多个基学习器(baselearner)来完成学习任务。集成学习的主要思想是"三个臭皮匠,顶个诸葛亮",即通过组合多个弱学习器来获得一个强学习器。集成学习方法主要分为两大类:Bagging(BootstrapAggregating):并行训练多个基学习器,然后通过投票
- 板凳-------Mysql cookbook学习 (十一--------2)
fengye207161
mysql学习数据库
11.6扩展序列列的取值范围2025-07-0111.7序列顶部数值的再使用11.8确保各行按照给定顺序重编号思路1、创建表的空克隆2、使用insertinto......select从源表自制行3、删除源表,并将克隆表重命名为源表表名4、如果是巨大的MyISAM,并含有多个索引,创建新表时不定义除了auto_increment列之外的索引,会使整个过程更高效重新编号时解决主键冲突的示例通过一个完
- Spark on Docker:容器化大数据开发环境搭建指南
AI天才研究院
ChatGPT实战ChatGPTAI大模型应用入门实战与进阶大数据sparkdockerai
SparkonDocker:容器化大数据开发环境搭建指南关键词:Spark、Docker、容器化、大数据开发、分布式计算、开发环境搭建、容器编排摘要:本文系统讲解如何通过Docker实现Spark开发环境的容器化部署,涵盖从基础概念到实战部署的完整流程。首先分析Spark分布式计算框架与Docker容器技术的核心原理及融合优势,接着详细演示单节点开发环境和多节点集群环境的搭建步骤,包括Docker
- 机器学习在智能金融风险评估中的应用:信用评分与欺诈检测
Blossom.118
机器学习与人工智能机器人机器学习人工智能python深度学习sklearn计算机视觉
在金融行业,风险评估是确保金融机构稳健运营的关键环节。随着大数据和机器学习技术的快速发展,金融机构开始探索如何利用机器学习算法来提高风险评估的准确性和效率。本文将探讨机器学习在智能金融风险评估中的应用,特别是信用评分和欺诈检测方面的最新进展,并分析其带来的机遇和挑战。一、智能金融风险评估中的信用评分(一)传统信用评分方法的局限性传统的信用评分主要依赖于人工规则和简单的统计模型,如逻辑回归。这些方法
- 用这些中医 APP,开启免费自学之旅!问止精一书院
2501_92057656
自学中医
零基础学中医学中医如何入门免费学中医!问止精一书院链接:https://tool.nineya.com/qrcode/1iv54b4ts在众多中医学习网站中,问止中医凭借专为零基础者打造的免费课程脱颖而出,成为中医入门者的理想之选。对于想要学习中医却毫无基础的人来说,选对平台至关重要。问止中医深知零基础学习者的痛点,其免费报名课程从中医基础理论讲起,像阴阳五行、脏腑经络等核心知识,都以通俗易懂的方
- 45 岁学医晚吗?告诉你最晚不能超过的年龄
2501_92275177
学中医如何入门零基础学中医
零基础学中医学中医如何入门免费学中医!问止精一书院链接:https://tool.nineya.com/qrcode/1iv54b4ts常有45岁的朋友问:“现在学医晚吗?”作为一名46岁才开始接触中医的学习者,我可以肯定地说:不晚!但要选对入门方式,而问止中医的免费报名课程,就是帮你打破年龄顾虑的绝佳跳板。很多人纠结“最晚不能超过多少岁”,其实中医学习更看重方法而非年龄。问止中医的免费课程专为中
- 机器学习在智能制造业中的应用:质量检测与设备故障预测
Blossom.118
机器学习与人工智能机器学习人工智能深度学习神经网络机器人sklearntensorflow
随着工业4.0和智能制造的推进,制造业正经历着一场深刻的数字化转型。智能制造业通过整合物联网(IoT)、大数据和机器学习等先进技术,实现从生产计划到质量控制的全流程优化。机器学习技术在智能制造业中的应用尤为突出,尤其是在质量检测和设备故障预测方面。本文将探讨机器学习在智能制造业中的应用,并分析其带来的机遇和挑战。一、智能制造业中的质量检测(一)传统质量检测方法的局限性传统的质量检测主要依赖于人工检
- Chart.js 安装使用教程
小奇JAVA面试
安装使用教程javascript开发语言ecmascript
一、Chart.js简介Chart.js是一个简单而灵活的JavaScript图表库,支持8种常用图表类型(折线图、柱状图、饼图等),基于HTML5Canvas渲染。它轻量易用,适合快速构建响应式图表,广泛应用于仪表盘、可视化后台、统计图展示等场景。二、Chart.js安装方式2.1使用CDN引入(推荐快速使用)2.2使用npm安装(适合前端工程项目)npminstallchart.js--sav
- 面了字节跳动的数据挖掘岗,感觉真的很难。。。
大模型爱好者社区
机器学习深度学习面试宝典数据挖掘人工智能数据分析算法面试
节前,我们社群组织了一场技术&面试讨论会,邀请了一些互联网大厂同学、参加社招和校招面试的同学,针对新手如何入门机器学习算法、该如何备战、面试常考点分享等热门话题进行了深入的讨论。基于社群的讨论,今天我整理了一个同学的面试题,分享给大家,希望对后续找工作的有所帮助。喜欢记得点赞、收藏、关注。更多技术交流&面经学习,可以文末加入我们交流群。一面40min【编程题】有两种数据,分别是被转发的用户和转发的
- 【字节跳动】数据挖掘面试题0002:从转发数据中求原视频用户以及转发的最长深度和二叉排序树指定值
言析数智
数据挖掘常见面试题数据挖掘面试题
文章大纲题目一:从转发数据中求原视频用户以及转发的最长深度问题分析解题思路寻找原视频用户计算转发最长深度题目二:在一棵二叉排序树中,找到比给定数值小的最大节点方法思路题目一:从转发数据中求原视频用户以及转发的最长深度在数据处理和算法面试中,常常会遇到一些基于实际业务场景的题目,比如根据用户转发数据来分析原视频用户以及转发深度。今天就来探讨一道这样的面试题:给定被转发用户和转发用户两组数据,求原视频
- 使用NPM安装Highcharts的完整指南
祁泉望Ernestine
使用NPM安装Highcharts的完整指南highcharts项目地址:https://gitcode.com/gh_mirrors/high/highcharts前言Highcharts作为一款功能强大的数据可视化库,在现代Web开发中扮演着重要角色。本文将详细介绍如何通过NPM包管理器来安装和使用Highcharts及其相关产品(Stock、Maps和Gantt),帮助开发者快速上手这一优秀
- 全流程文献计量学可视化分析技术及SCI论文高效写作方法
青春不败 177-3266-0520
生态环境人工智能python文献可视化SCI论文生态学环境科学遥感
文献计量学是指用数学和统计学的方法,定量地分析一切知识载体的交叉科学。它是集数学、统计学、文献学为一体,注重量化的综合性知识体系。特别是,信息可视化技术手段和方法的运用,可直观的展示主题的研究发展历程、研究现状、研究热点和发展态势。一:文献计量学方法与应用1.文献计量学方法基本2.与其他综述方法区别联系3.各学科领域应用趋势近况4.主流分析软件优缺点对比二:主题确定、检索与数据采集1.热点主题高效
- 【字节跳动】数据挖掘面试题0001:打车场景下POI与ODR空间关联查询
言析数智
数据挖掘常见面试题数据挖掘人工智能面试题
题目描述打车的场景下,poi记录了建筑物的坐标:poi(pid,x,y),odr记录的是乘客上车点的坐标:odr(oid,x,y);希望对所有的poi,获得其周围的100m的odr:结果(pid,oid)打车场景下POI与ODR空间关联查询在打车场景中,我们经常需要将建筑物坐标(POI)与乘客上车点(ODR)进行空间关联分析。这个问题本质上是一个空间连接(SpatialJoin)问题,需要找到距离
- 3步打造Java六边形帝国!解耦业务逻辑全攻略:破解5大陷阱!
墨瑾轩
一起学学C#【三】java开发语言
关注墨瑾轩,带你探索编程的奥秘!超萌技术攻略,轻松晋级编程高手技术宝库已备好,就等你来挖掘订阅墨瑾轩,智趣学习不孤单即刻启航,编程之旅更有趣**六边形架构的“3步魔法召唤术”**第一步:定义核心业务逻辑——给业务装上“女王皇冠”!定义:“就像给业务女王颁发‘独立宣言’,用纯业务类和接口定义核心逻辑!”案例①:订单服务核心逻
- C#图片变视频:三步召唤‘AVI魔术师’——对比FFmpeg,代码实战全解析!
墨瑾轩
一起学学C#【七】c#音视频ffmpeg
关注墨瑾轩,带你探索编程的奥秘!超萌技术攻略,轻松晋级编程高手技术宝库已备好,就等你来挖掘订阅墨瑾轩,智趣学习不孤单即刻启航,编程之旅更有趣SharpAvi图片转AVI全攻略1.环境准备:先装“魔法道具包”目标:从“零基础”到“代码运行”,三步搞定!1.1安装SharpAvi方法1:通过NuGet安装
- 免费学中医,这些优质资源不容错过
少林659
零基础学中医免费学中医
零基础学中医,学中医如何入门免费学中医!问止精一书院链接:https://tool.nineya.com/qrcode/1iv54b4ts想入门中医却担心成本太高?其实有不少免费又优质的学习资源,问止中医的系列免费课程就是其中的佼佼者,涵盖理论与实操,满足不同学习者的需求。问止中医旗下的精一书院,是免费学中医的绝佳平台。由问止中医联合创始人林大栋博士主讲,课程聚焦中医结构分析、人工智能中医大脑技术
- 两个点 定位_基于双天线的北斗定位系统设计与实现
weixin_39697096
两个点定位
前期实际北斗模块定位误差统计分析中得出了北斗模块的定位误差分布服从正态分布,根据北斗模块定位误差分布的规律,利用在同一块电路板上的双天线模块接收北斗定位信号,将定位信息传给TMS320F28335DSP芯片,DSP对北斗模块给出的定位信息做实时算法处理,并将处理后的定位信息传给嵌入式ARM芯片,ARM芯片在TFT液晶屏上更新定位信息,同时根据用户要求来设置北斗模块的工作模式。在接收不到北斗定位信息
- JVM调优实战 Day 7:JVM线程分析与死锁排查
在未来等你
JVM调优实战JVMJava性能优化调优虚拟机
【JVM调优实战Day7】JVM线程分析与死锁排查文章标签jvm调优,线程分析,死锁排查,JVM监控,Java性能优化,JVM参数配置文章简述在Java应用的高并发场景中,线程管理与死锁问题往往是性能瓶颈的根源。本文作为“JVM调优实战”系列的第7天,深入解析JVM线程模型、死锁机制及其诊断方法。文章从线程的基本概念出发,结合实际案例,详细讲解如何使用JVM内置工具进行线程状态分析和死锁检测,并提
- RESTful API 设计原则深度解析
大曰编程
java面试后端
在Web服务架构中,RESTfulAPI作为一种轻量级、可扩展的接口设计风格,通过HTTP协议实现资源的标准化访问。本文从核心原则、URL设计、HTTP方法应用、状态管理及面试高频问题五个维度,结合工程实践与反例分析,系统解析RESTfulAPI的设计规范与最佳实践。一、RESTful核心原则与架构约束1.1六大核心原则原则定义设计目标资源导向以资源(Resource)为核心,而非操作(如“用户”
- JWT认证性能优化实战指南
JWT认证性能优化实战指南一、技术背景与应用场景随着微服务与云原生架构的普及,基于Token的认证方式成为保证系统安全与可扩展性的首选方案。JWT(JSONWebToken)以其自包含、自验证、跨语言支持等优点,在分布式环境中广泛应用。但在高并发场景下,JWT的解析、签名与验证过程可能成为性能瓶颈。本篇文章将结合真实生产环境,深入剖析JWT认证的核心原理,重点分析性能瓶颈,并提供多种可落地的优化实
- 【Linux】vim工具
nanguochenchuan
Linux操作系统linuxvim运维
Vim简介与应用场景Vim(ViImproved)作为一款源自Unix系统vi编辑器的增强版本,以其独特的模式化编辑和全键盘操作闻名。主要特点包括:轻量级:仅需几MB空间,适合服务器环境高度可定制:通过.vimrc和插件实现个性化配置跨平台:支持Linux、macOS、Windows等系统典型应用场景:服务器远程管理(通过SSH连接时的高效编辑)编程开发(支持300+语言的语法高亮)日志文件分析(
- Elasticsearch性能调优金字塔:从分片与副本策略构建海量日志分析平台
lingRJ777
Java技术栈应用javabackendelasticsearchspringbootmicroserviceselk
Elasticsearch性能调优金字塔:从分片与副本策略构建海量日志分析平台引言在当前的微服务架构体系中,一个复杂的业务流程往往会横跨数十甚至上百个服务。当线上出现问题时,如何从每天产生的TB级海量日志中快速定位根源,成为衡量系统可观测性的关键。传统的日志聚合方案在面对如此巨大的数据量时,普遍会遇到两大核心挑战:高并发写入瓶颈:数千个服务实例同时产生大量日志,要求日志系统具备极高的写入吞吐能力,
- 路由器工作在OSI模型的哪一层?
路由器主要工作在OSI模型的第三层,即网络层。网络层的主要功能是将数据包从源地址路由到目标地址,路由器通过检查数据包中的目标IP地址,并根据路由表确定最佳路径来实现这一功能。路由器的主要功能:a、路由决策:路由器通过分析目标IP地址,决定数据包的转发路径。b、跨网络通信:负责不同网络之间的数据传输。c、网络互联:连接多个网络,实现广域网或局域网之间的通信。d、路由表维护:通过直连路由、静态路由和动
- 【深度学习-Day 33】从零到一:亲手构建你的第一个卷积神经网络(CNN)
吴师兄大模型
深度学习入门到精通深度学习cnn人工智能python大模型卷积神经网络(CNN)机器学习
Langchain系列文章目录01-玩转LangChain:从模型调用到Prompt模板与输出解析的完整指南02-玩转LangChainMemory模块:四种记忆类型详解及应用场景全覆盖03-全面掌握LangChain:从核心链条构建到动态任务分配的实战指南04-玩转LangChain:从文档加载到高效问答系统构建的全程实战05-玩转LangChain:深度评估问答系统的三种高效方法(示例生成、手
- C#架构可扩展性终极指南:3招让代码像变形金刚一样灵活!
墨瑾轩
一起学学C#【七】c#架构开发语言
关注墨瑾轩,带你探索编程的奥秘!超萌技术攻略,轻松晋级编程高手技术宝库已备好,就等你来挖掘订阅墨瑾轩,智趣学习不孤单即刻启航,编程之旅更有趣C#架构可扩展性的“超能力”实战指南秘籍1:模块解耦——给代码装“乐高积木”核心思想:模块化是代码的“变形引擎”,用接口和依赖注入(DI)让模块像乐高一样自由拼装!1.1问题场景:硬编码依赖的“灾难现场”
- JAVA基础
灵静志远
位运算加载Date字符串池覆盖
一、类的初始化顺序
1 (静态变量,静态代码块)-->(变量,初始化块)--> 构造器
同一括号里的,根据它们在程序中的顺序来决定。上面所述是同一类中。如果是继承的情况,那就在父类到子类交替初始化。
二、String
1 String a = "abc";
JAVA虚拟机首先在字符串池中查找是否已经存在了值为"abc"的对象,根
- keepalived实现redis主从高可用
bylijinnan
redis
方案说明
两台机器(称为A和B),以统一的VIP对外提供服务
1.正常情况下,A和B都启动,B会把A的数据同步过来(B is slave of A)
2.当A挂了后,VIP漂移到B;B的keepalived 通知redis 执行:slaveof no one,由B提供服务
3.当A起来后,VIP不切换,仍在B上面;而A的keepalived 通知redis 执行slaveof B,开始
- java文件操作大全
0624chenhong
java
最近在博客园看到一篇比较全面的文件操作文章,转过来留着。
http://www.cnblogs.com/zhuocheng/archive/2011/12/12/2285290.html
转自http://blog.sina.com.cn/s/blog_4a9f789a0100ik3p.html
一.获得控制台用户输入的信息
&nbs
- android学习任务
不懂事的小屁孩
工作
任务
完成情况 搞清楚带箭头的pupupwindows和不带的使用 已完成 熟练使用pupupwindows和alertdialog,并搞清楚两者的区别 已完成 熟练使用android的线程handler,并敲示例代码 进行中 了解游戏2048的流程,并完成其代码工作 进行中-差几个actionbar 研究一下android的动画效果,写一个实例 已完成 复习fragem
- zoom.js
换个号韩国红果果
oom
它的基于bootstrap 的
https://raw.github.com/twbs/bootstrap/master/js/transition.js transition.js模块引用顺序
<link rel="stylesheet" href="style/zoom.css">
<script src=&q
- 详解Oracle云操作系统Solaris 11.2
蓝儿唯美
Solaris
当Oracle发布Solaris 11时,它将自己的操作系统称为第一个面向云的操作系统。Oracle在发布Solaris 11.2时继续它以云为中心的基调。但是,这些说法没有告诉我们为什么Solaris是配得上云的。幸好,我们不需要等太久。Solaris11.2有4个重要的技术可以在一个有效的云实现中发挥重要作用:OpenStack、内核域、统一存档(UA)和弹性虚拟交换(EVS)。
- spring学习——springmvc(一)
a-john
springMVC
Spring MVC基于模型-视图-控制器(Model-View-Controller,MVC)实现,能够帮助我们构建像Spring框架那样灵活和松耦合的Web应用程序。
1,跟踪Spring MVC的请求
请求的第一站是Spring的DispatcherServlet。与大多数基于Java的Web框架一样,Spring MVC所有的请求都会通过一个前端控制器Servlet。前
- hdu4342 History repeat itself-------多校联合五
aijuans
数论
水题就不多说什么了。
#include<iostream>#include<cstdlib>#include<stdio.h>#define ll __int64using namespace std;int main(){ int t; ll n; scanf("%d",&t); while(t--)
- EJB和javabean的区别
asia007
beanejb
EJB不是一般的JavaBean,EJB是企业级JavaBean,EJB一共分为3种,实体Bean,消息Bean,会话Bean,书写EJB是需要遵循一定的规范的,具体规范你可以参考相关的资料.另外,要运行EJB,你需要相应的EJB容器,比如Weblogic,Jboss等,而JavaBean不需要,只需要安装Tomcat就可以了
1.EJB用于服务端应用开发, 而JavaBeans
- Struts的action和Result总结
百合不是茶
strutsAction配置Result配置
一:Action的配置详解:
下面是一个Struts中一个空的Struts.xml的配置文件
<?xml version="1.0" encoding="UTF-8" ?>
<!DOCTYPE struts PUBLIC
&quo
- 如何带好自已的团队
bijian1013
项目管理团队管理团队
在网上看到博客"
怎么才能让团队成员好好干活"的评论,觉得写的比较好。 原文如下: 我做团队管理有几年了吧,我和你分享一下我认为带好团队的几点:
1.诚信
对团队内成员,无论是技术研究、交流、问题探讨,要尽可能的保持一种诚信的态度,用心去做好,你的团队会感觉得到。 2.努力提
- Java代码混淆工具
sunjing
ProGuard
Open Source Obfuscators
ProGuard
http://java-source.net/open-source/obfuscators/proguardProGuard is a free Java class file shrinker and obfuscator. It can detect and remove unused classes, fields, m
- 【Redis三】基于Redis sentinel的自动failover主从复制
bit1129
redis
在第二篇中使用2.8.17搭建了主从复制,但是它存在Master单点问题,为了解决这个问题,Redis从2.6开始引入sentinel,用于监控和管理Redis的主从复制环境,进行自动failover,即Master挂了后,sentinel自动从从服务器选出一个Master使主从复制集群仍然可以工作,如果Master醒来再次加入集群,只能以从服务器的形式工作。
什么是Sentine
- 使用代理实现Hibernate Dao层自动事务
白糖_
DAOspringAOP框架Hibernate
都说spring利用AOP实现自动事务处理机制非常好,但在只有hibernate这个框架情况下,我们开启session、管理事务就往往很麻烦。
public void save(Object obj){
Session session = this.getSession();
Transaction tran = session.beginTransaction();
try
- maven3实战读书笔记
braveCS
maven3
Maven简介
是什么?
Is a software project management and comprehension tool.项目管理工具
是基于POM概念(工程对象模型)
[设计重复、编码重复、文档重复、构建重复,maven最大化消除了构建的重复]
[与XP:简单、交流与反馈;测试驱动开发、十分钟构建、持续集成、富有信息的工作区]
功能:
- 编程之美-子数组的最大乘积
bylijinnan
编程之美
public class MaxProduct {
/**
* 编程之美 子数组的最大乘积
* 题目: 给定一个长度为N的整数数组,只允许使用乘法,不能用除法,计算任意N-1个数的组合中乘积中最大的一组,并写出算法的时间复杂度。
* 以下程序对应书上两种方法,求得“乘积中最大的一组”的乘积——都是有溢出的可能的。
* 但按题目的意思,是要求得这个子数组,而不
- 读书笔记-2
chengxuyuancsdn
读书笔记
1、反射
2、oracle年-月-日 时-分-秒
3、oracle创建有参、无参函数
4、oracle行转列
5、Struts2拦截器
6、Filter过滤器(web.xml)
1、反射
(1)检查类的结构
在java.lang.reflect包里有3个类Field,Method,Constructor分别用于描述类的域、方法和构造器。
2、oracle年月日时分秒
s
- [求学与房地产]慎重选择IT培训学校
comsci
it
关于培训学校的教学和教师的问题,我们就不讨论了,我主要关心的是这个问题
培训学校的教学楼和宿舍的环境和稳定性问题
我们大家都知道,房子是一个比较昂贵的东西,特别是那种能够当教室的房子...
&nb
- RMAN配置中通道(CHANNEL)相关参数 PARALLELISM 、FILESPERSET的关系
daizj
oraclermanfilespersetPARALLELISM
RMAN配置中通道(CHANNEL)相关参数 PARALLELISM 、FILESPERSET的关系 转
PARALLELISM ---
我们还可以通过parallelism参数来指定同时"自动"创建多少个通道:
RMAN > configure device type disk parallelism 3 ;
表示启动三个通道,可以加快备份恢复的速度。
- 简单排序:冒泡排序
dieslrae
冒泡排序
public void bubbleSort(int[] array){
for(int i=1;i<array.length;i++){
for(int k=0;k<array.length-i;k++){
if(array[k] > array[k+1]){
- 初二上学期难记单词三
dcj3sjt126com
sciet
concert 音乐会
tonight 今晚
famous 有名的;著名的
song 歌曲
thousand 千
accident 事故;灾难
careless 粗心的,大意的
break 折断;断裂;破碎
heart 心(脏)
happen 偶尔发生,碰巧
tourist 旅游者;观光者
science (自然)科学
marry 结婚
subject 题目;
- I.安装Memcahce 1. 安装依赖包libevent Memcache需要安装libevent,所以安装前可能需要执行 Shell代码 收藏代码
dcj3sjt126com
redis
wget http://download.redis.io/redis-stable.tar.gz
tar xvzf redis-stable.tar.gz
cd redis-stable
make
前面3步应该没有问题,主要的问题是执行make的时候,出现了异常。
异常一:
make[2]: cc: Command not found
异常原因:没有安装g
- 并发容器
shuizhaosi888
并发容器
通过并发容器来改善同步容器的性能,同步容器将所有对容器状态的访问都串行化,来实现线程安全,这种方式严重降低并发性,当多个线程访问时,吞吐量严重降低。
并发容器ConcurrentHashMap
替代同步基于散列的Map,通过Lock控制。
&nb
- Spring Security(12)——Remember-Me功能
234390216
Spring SecurityRemember Me记住我
Remember-Me功能
目录
1.1 概述
1.2 基于简单加密token的方法
1.3 基于持久化token的方法
1.4 Remember-Me相关接口和实现
- 位运算
焦志广
位运算
一、位运算符C语言提供了六种位运算符:
& 按位与
| 按位或
^ 按位异或
~ 取反
<< 左移
>> 右移
1. 按位与运算 按位与运算符"&"是双目运算符。其功能是参与运算的两数各对应的二进位相与。只有对应的两个二进位均为1时,结果位才为1 ,否则为0。参与运算的数以补码方式出现。
例如:9&am
- nodejs 数据库连接 mongodb mysql
liguangsong
mongodbmysqlnode数据库连接
1.mysql 连接
package.json中dependencies加入
"mysql":"~2.7.0"
执行 npm install
在config 下创建文件 database.js
- java动态编译
olive6615
javaHotSpotjvm动态编译
在HotSpot虚拟机中,有两个技术是至关重要的,即动态编译(Dynamic compilation)和Profiling。
HotSpot是如何动态编译Javad的bytecode呢?Java bytecode是以解释方式被load到虚拟机的。HotSpot里有一个运行监视器,即Profile Monitor,专门监视
- Storm0.9.5的集群部署配置优化
roadrunners
优化storm.yaml
nimbus结点配置(storm.yaml)信息:
# Licensed to the Apache Software Foundation (ASF) under one
# or more contributor license agreements. See the NOTICE file
# distributed with this work for additional inf
- 101个MySQL 的调节和优化的提示
tomcat_oracle
mysql
1. 拥有足够的物理内存来把整个InnoDB文件加载到内存中——在内存中访问文件时的速度要比在硬盘中访问时快的多。 2. 不惜一切代价避免使用Swap交换分区 – 交换时是从硬盘读取的,它的速度很慢。 3. 使用电池供电的RAM(注:RAM即随机存储器)。 4. 使用高级的RAID(注:Redundant Arrays of Inexpensive Disks,即磁盘阵列
- zoj 3829 Known Notation(贪心)
阿尔萨斯
ZOJ
题目链接:zoj 3829 Known Notation
题目大意:给定一个不完整的后缀表达式,要求有2种不同操作,用尽量少的操作使得表达式完整。
解题思路:贪心,数字的个数要要保证比∗的个数多1,不够的话优先补在开头是最优的。然后遍历一遍字符串,碰到数字+1,碰到∗-1,保证数字的个数大于等1,如果不够减的话,可以和最后面的一个数字交换位置(用栈维护十分方便),因为添加和交换代价都是1
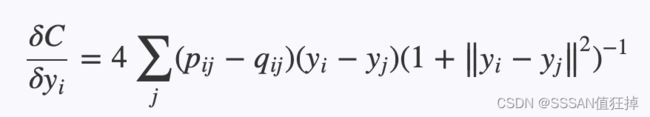
 )
) )
)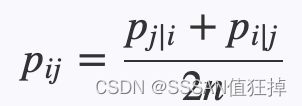 )
)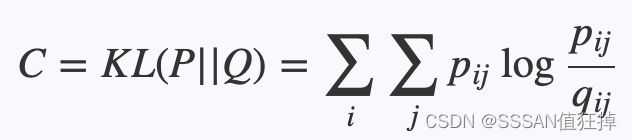 )
)